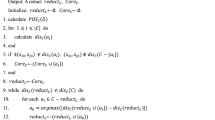A unified incremental reduction with the variations of the object for decision tables

Abstract

Attribute reduction is one of the issues in the rough set theory, and many reduction algorithms have been proposed to process the static decision systems. However, in real-life applications, the object may vary dynamically with time. In order to deal with common variations of the object (i.e., adding the object, deleting the object and modifying the object’s value) in the decision systems, the paper presents a unified incremental reduction algorithm for three types of the dynamic object from the viewpoint of the discernibility matrix. Firstly, the concepts of the equivalence class linked table (ECLT) and the simplified decision table are proposed. On the basis of ECLT, the incremental mechanisms are analyzed and the corresponding functions for updating the discernibility matrix are designed for three variations of the object. And then, the dynamic criterions how to add new attributes into the original reduct or delete redundant attributes from the original reduct are studied. Subsequently, a unified incremental reduction algorithm with varying the object is presented. A serial of experiments are validated to explain the feasibility and effectiveness of the proposed algorithms on different data sets from UCI.

Appendix A. Related proof of proposed theorems and propositions

1.1 Proof of Theorem 1

Proof

(1) Firstly, prove $\hbox {Core}(C)\subseteq \hbox {Core}'(C)$. Only prove that $\forall a\in \hbox {Core}(C)$, then $a\in \hbox {Core}'(C)$.

Because of $a\in \hbox {Core}(C)$, it follows that there exists $x_{i}\in U$ which satisfies $x_{i}\in \hbox {POS}_{C}(D)$ but $x_{i}\notin \hbox {POS}_{C-\{a\}}(D)$, namely $f(x_{i},C-\{a\})=f(x_{j},C-\{a\})\wedge f(x_{i},a)\ne f(x_{j},a)\wedge f(x_{i},D)\ne { f}(x_{j},D)$. Suppose $x_{i}\in [x'_{i}]_{C}$ and $x_{j}\in [x'_{j}]_{C}$, then $f(x'_{i},C-\{a\})=f(x'_{j},C-\{a\})\wedge f(x'_{i},a)\ne f(x'_{j},a)$. Since $x_{i}\in \hbox {POS}_{C}(D)$, then $x'_{i}\in \hbox {POS}_{C}(D)$. $x_{j}$ exists two cases: (i) $x_{j}\in \hbox {POS}_{C}(D)$, then $x'_{j}\in \hbox {POS}_{C}(D)$ and $f(x'_{i},D)\ne { f}(x'_{j},D)$. From $x'_{i}$, $x'_{j}\in \hbox {POS}_{C}(D)$, we have $x'_{i}$, $x'_{j}\in U_{1}'$. We can attain $m_{ij}=\{a\}$, then $a\in \hbox {Core}'(C)$. (ii) $x_{j}\notin \hbox {POS}_{C}(D)$, then $x'_{j}\notin \hbox {POS}_{C}(D)$. Because of $x'_{i}\in \hbox {POS}_{C}(D)$, from Definition 1, we can attain $x'_{i}\in U_{1}'$ and $x'_{j}\in U_{2}'$; from Definition 2 and Definition 3, we can attain $m_{ij}=\{a\}$, then $a\in \hbox {Core}'(C)$. Hence, $a\in \hbox {Core}'(C)$.

(2) Secondly, prove $\hbox {Core}'(C)\subseteq \hbox {Core}~(C)$. Only prove that $\forall a\in \hbox {Core}'(C)$, then $a\in \hbox {Core}(C)$.

Because of $a\in \hbox {Core}'(C)$, it follows that there exists $m_{ij}\in {{\varvec{M}}}$ and $m_{ij}=\{a\}$, namely $\exists \, x_{i}$, $x_{j}\in U'$, $f(x_{i},a)\ne f(x_{j},a)\wedge f(x_{i},C-\{a\})=f(x_{j},C-\{a\})$. At least $\exists \, x_{i}\in U_{1}'$ or $x_{j}\in U_{1}'$, suppose $x_{i}\in U_{1}'$, then $x_{i}\in \hbox {POS}_{C}(D)$. $x_{j}$ exists two cases: (i) $x_{j}\in U_{1}'$, then $f(x_{i},a)\ne f(x_{j},a)\wedge f(x_{i},C-\{a\})=f(x_{j},C-\{a\})\wedge f(x_{i},D)\ne { f}(x_{j},D)$, so that $x_{i}\notin \hbox {POS}_{C-\{a\}}(D)$. (ii) $x_{j}\in U_{2}'$, suppose $\exists \, x'_{j}\in [x_{j}]_{C}$, then $f(x_{i},D)\ne { f}(x'_{j},D)$. Similarly (i), we can gain $x_{i}\notin \hbox {POS}_{C-\{a\}}(D)$. From (i) and (ii) we can get $\hbox {POS}_{C-\{a\}}(D)\ne \hbox {POS}_{C}(D)$, so that $a\in \hbox {Core}(C)$.

From (1) and (2), Theorem 2 can be proved. $\square$

1.2 Proof of Theorem 2

Proof

First, we pove that $R\subseteq C$ and $R\in { RedM}$, then $R\in { Red}$.

• (1) Firstly, prove $\forall R\in { RedM}$, then $\hbox {POS}_{R}(D)=\hbox {POS}_{C}(D)$.

Prove to the reverse. Suppose that $\exists \, R\in { RedM}$ and $\hbox {POS}_{R}(D)\ne \hbox {POS}_{C}(D)$, then at least $\exists \, x_{i}\in U$ and $x_{i}\in \hbox {POS}_{C}(D)$, but $x_{i}\notin \hbox {POS}_{R}(D)$. According to Definition 1, then $f(x_{i},D)\ne V_{\xi }'$. Since $x_{i}\notin \hbox {POS}_{R}(D)$, we have $\exists \, x_{j}\in U (x_{j}\ne x_{i})$ and $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. $x_{j}$ exists two cases: (i) $x_{j}\in \hbox {POS}_{C}(D)$. From Definition 1, we can obtain $f(x_{j},D)\ne V_{\xi }'$, and $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. By Definition 4, we have $R\cap m_{ij}=\varPhi$. (ii) $x_{j}\notin \hbox {POS}_{C}(D)$. From Definition 1, we can have $f(x_{j},D)=V_{\xi }'$, and $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$, then $R\cap m_{ij}=\varPhi$. From (i) and (ii), we can get $R\cap m_{ij}=\varPhi$, which is conflict with condition (1) of Definition 4. Therefore, the hypothesis is not valid and have $\hbox {POS}_{R}(D)=\hbox {POS}_{C}(D)$.

• (2) Secondly, prove $\forall R\in { RedM}$ and $\forall a\in R$, then $\hbox {POS}_{C}(D)\ne \hbox {POS}_{R-\{a\}}(D)$.

Prove to the reverse. Assume that $R\in { RedM}$ and $\exists \, a\in R$, there exists $\hbox {POS}_{C}(D)=\hbox {POS}_{R-\{a\}}(D)$. From (1), we have $\hbox {POS}_{R}(D)=\hbox {POS}_{C}(D)$, then $\hbox {POS}_{R}(D)=\hbox {POS}_{R-\{a\}}(D)$. Because of $\forall \varPhi \ne m_{ij}\in {{\varvec{M}}}$, $R\cap m_{ij}\ne \varPhi$, so for $x_{i},x_{j}\in U'$, we can obtain $f(x_{i},R)\ne f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$, one of $f(x_{i},D)\ne V_{\xi }'$ and $f(x_{j},D)\ne V_{\xi }'$ holds at least. So we suppose $f(x_{i},D)\ne V_{\xi }'$. There exist two cases for $f(x_{j},D)$: (i) $f(x_{j},D)\ne V_{\xi }$, then there necessarily exists $f(x_{i},R)\ne f(x_{j},R) \wedge f(x_{i},D)\ne f(x_{j},D)$. (ii) $f(x_{j},D)=V_{\xi }'$, there exists $x'_{j}\in U$ and $x'_{j}\in [x_{j}]_{C}$, but $f(x_{j},D)\ne f(x'_{j},D)$, then one of $f(x_{i},D)\ne f(x_{j},D)$ and $f(x_{i},D)\ne f(x'_{j},D)$ holds at least. Suppose $f(x_{i},D)\ne f(x_{j},D)$, there exists $f(x_{i},R)\ne f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. From (i) and (ii), we can have $f(x_{i},R)\ne f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. Since $m_{ij}$ is arbitrary, then $x_{i}\in \hbox {POS}_{R}(D)$. From $\hbox {POS}_{R}(D)=\hbox {POS}_{R-\{a\}}(D)$, we can have $x_{i}\in \hbox {POS}_{R-\{a\}}(D)$. From (i) and (ii), we know $f(x_{i},D)\ne f(x_{j},D)$. In order to meet $\hbox {POS}_{R}(D)=\hbox {POS}_{R-\{a\}}(D)$, there necessarily exists $f(x_{i}$, $R-\{a\})\ne f(x_{j},R-\{a\})$, and then have $f(x_{i},R-\{a\})\ne f(x_{j},R-\{a\})\wedge f(x_{i},D)\ne f(x_{j},D)$, so $R-\{a\}\cap m_{ij}\ne \varPhi$ which is conflict with condition (2) of Definition 4. Therefore, the hypothesis is not valid.

According to (1) (2), we can prove $R\in { RedM}$, then $R\in { Red}$$\square$

Then, we prove that $R\subseteq C$ and $R\in { Red}$, then $R\in { RedM}$.

Proof

(1) Firstly, prove $\forall R\in { Red}$, then $\forall \varPhi \ne m_{ij}\in {{\varvec{M}}}$ and $R\cap m_{ij}\ne \varPhi$.

Prove to the reverse. Assume that there exists $\varPhi \ne m_{ij}\in {{\varvec{M}}}$ and $R\cap m_{ij}=\varPhi$, i.e., we have $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. For $x_{i}$, $x_{j}\in U'$, one of $f(x_{i},D)\ne V_{\xi }$ and $f(x_{j},D)\ne V_{\xi }$ can hold at least. Suppose $f(x_{i},D)\ne V_{\xi }$, we have $x_{i}\in \hbox {POS}_{C}(D)$, and $x_{j}$ exists the following two cases: (i) $f(x_{j},D)\ne V_{\xi }'$, from Definition 1, there exists $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$ and then $x_{i}\notin \hbox {POS}_{R}(D)$. (ii) $f(x_{j},D)=V_{\xi }'$, suppose there exists $x'_{j}\in U$, $x'_{j}\in [x_{j}]_{C}$ and $f(x_{j},D)\ne f(x'_{j},D)$, then one of $f(x_{i},D)\ne f(x_{j},D)$ and $f(x_{i},D)\ne f(x'_{j},D)$ will hold at least. Suppose $f(x_{i},D)\ne f(x_{j},D)$, there exists $f(x_{i},R)=f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$, we can have $x_{i}\notin \hbox {POS}_{R}(D)$. From (i) and (ii), thus there exists $x_{i}$, $x_{i}\in \hbox {POS}_{C}(D)$, but $x_{i}\notin \hbox {POS}_{R}(D)$, so $\hbox {POS}_{R}(D)\ne \hbox {POS}_{C}(D)$, which is conflict with condition (1) of reduct definition. Therefore, the hypothesis is not valid.

(2) Secondly, prove $\forall R\in { Red}$ and $\forall a\in R$, then $\exists \,\varPhi \ne m_{ij}\in {{\varvec{M}}}$, $R-\{a\}\cap m_{ij}=\varPhi$.

Prove to the reverse. Assume that there exists $a\in R$, $\forall m_{ij}\ne \varPhi$ and $m_{ij}\cap R-\{a\}\ne \varPhi$, i.e., we have $f(x_{i},R-\{a\})\ne f(x_{j},R-\{a\})\wedge f(x_{i},D)\ne f(x_{j},D)$. One of $f(x_{i},D)\ne V_{\xi }'$ and $f(x_{j},D)\ne V_{\xi }'$ holds at least. Suppose $f(x_{i},D)\ne V_{\xi }'$, then $x_{j}$ exists the following two cases: (i) $f(x_{j},D)\ne V_{\xi }'$. From Definition 1, we have $f(x_{i},R-\{a\})\ne f(x_{j},R-\{a\})\wedge f(x_{i},D)\ne f(x_{j},D)$. (ii) $f(x_{j},D)=V_{\xi }'$. There exists $x'_{j}\in [x_{j}]_{C}$ and $f(x_{j},D)\ne f(x'_{j},D)$, then one of $f(x_{i},D)\ne f(x_{j},D)$ and $f(x_{i},D)\ne f(x'_{j},D)$ will hold at least. Assume that $f(x_{i},D)\ne f(x_{j},D)$, then we have $f(x_{i},R-\{a\})\ne f(x_{j},R-\{a\})\wedge f(x_{i},D)\ne f(x_{j},D)$. From (i) and (ii), $\forall x_{i}$, there necessarily exists $f(x_{i},R-\{a\})\ne f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. Since $m_{ij}$ is arbitrary, then $x_{i}\in \hbox {POS}_{R-\{a\}}(D)$.

From (1), we know $\forall \varPhi \ne m_{ij}\in {{\varvec{M}}}$ and $m_{ij}\cap R\ne \varPhi$, i.e., $f(x_{i},R)\ne f(x_{j},R)\wedge f(x_{i},D)\ne f(x_{j},D)$. Thus, we can obtain $x_{i}\in \hbox {POS}_{R}(D)$, so that $\hbox {POS}_{R}(D)=\hbox {POS}_{R-\{a\}}(D)$, which is conflict with condition (2) of reduct definition. Therefore, the hypothesis is not valid.

According to (1) and (2), we can prove $\forall R\subseteq C$ and $R\in { Red}$, then $R\in { RedM}$. $\square$

Hence, Theorem 2 holds.