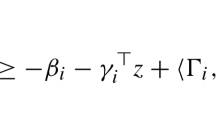Abstract
Given a set of line segments in the plane, not necessarily finite, what is a convex region of smallest area that contains a translate of each input segment? This question can be seen as a generalization of Kakeya’s problem of finding a convex region of smallest area such that a needle can be rotated through 360 degrees within this region. We show that there is always an optimal region that is a triangle, and we give an optimal Θ(nlogn)-time algorithm to compute such a triangle for a given set of n segments. We also show that, if the goal is to minimize the perimeter of the region instead of its area, then placing the segments with their midpoint at the origin and taking their convex hull results in an optimal solution. Finally, we show that for any compact convex figure G, the smallest enclosing disk of G is a smallest-perimeter region containing a translate of every rotated copy of G.










Similar content being viewed by others
References
Ahn, H., Cheong, O.: Aligning two convex figures to minimize area or perimeter. Algorithmica 62, 464–479 (2012)
Ben-Or, M.: Lower bounds for algebraic computation trees. In: Proceedings of the 15th Annual ACM Symposium on Theory of Computing, pp. 80–86 (1983)
Besicovitch, A.: Sur deux questions de l’intégrabilité des fonctions. J. Soc. Math. Phys. 2, 105–123 (1919)
Besicovitch, A.: On Kakeya’s problem and a similar one. Math. Z. 27, 312–320 (1928)
Besicovitch, A.: The Kakeya problem. Am. Math. Mon. 70, 697–706 (1963)
Besicovitch, A.: On fundamental geometric properties of plane line sets. J. Lond. Math. Soc. 39, 441–448 (1964)
Bezdek, K., Connelly, R.: Covering curves by translates of a convex set. Am. Math. Mon. 96, 789–806 (1989)
Bezdek, K., Connelly, R.: The minimum mean width translation cover for sets of diameter one. Beitr. Algebra Geom. 39, 473–479 (1998)
Bourgain, J.: Harmonic analysis and combinatorics: how much may they contribute to each other? In: Arnold, V., Atiyah, M., Lax, P., Mazur, B. (eds.) Mathematics: Frontiers and Perspectives, pp. 13–32. American Mathematical Society, Providence (2000)
Chakerian, G.: Sets of constant width. Pac. J. Math. 19, 13–21 (1966)
do Carmo, M.: Differential Geometry of Curves and Surfaces. Prentice-Hall, New York (1976)
Fejes Tóth, L.: On the densest packing of convex disks. Mathematika 30, 1–3 (1983)
Fisher, B.: On a problem of Besicovitch. Am. Math. Mon. 80(7), 785–787 (1973)
Jung, H.: Über die kleinste Kugel, die eine räumliche Figur einschliesst. J. Reine Angew. Math. 123, 241–257 (1901)
Kakeya, S.: Some problems on maximum and minimum regarding ovals. Tohoku Sci. Rep. 6, 71–88 (1917)
Laba, I.: From harmonic analysis to arithmetic combinatorics. Bull., New Ser., Am. Math. Soc. 45(1), 77–115 (2008)
Ohmann, D.: Extremalprobleme für konvexe Bereiche der euklidischen Ebene. Math. Z. 55, 346–352 (1952)
Pál, G.: Ein Minimumproblem für Ovale. Math. Ann. 83, 311–319 (1921)
Perron, O.: Über einen Satz von Besicovitch. Math. Z. 28, 383–386 (1928)
Rademacher, H.: On a theorem from Besicovitch. In: Szego, G. (ed.) Studies in Mathematical Analysis and Related Topics: Essays in Honor of George Pòlya, pp. 294–296. Stanford University Press, Stanford (1962)
Schneider, R.: Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge (1993)
Schoenberg, I.: On certain minima related to the Besicovitch-Kakeya problem. Mathematika 4(27), 145–148 (1962)
Schoenberg, I.: On the Besicovitch–Perron solution of the Kakeya problem. In: Szego, G. (ed.) Studies in Mathematical Analysis and Related Topics: Essays in Honor of George Pòlya, pp. 359–363. Stanford University Press, Stanford (1962)
Strang, G.: Maximum area with Minkowski measures of perimeter. Proc. R. Soc. Edinb. 138A, 189–199 (2008)
Tao, T.: From rotating needles to stability of waves: emerging connections between combinatorics, analysis and PDE. Not. Am. Math. Soc. 48(3), 297–303 (2001)
Toussaint, G.: Solving geometric problems with the rotating calipers. In: Proceedings of IEEE MELECON, pp. 1–4 (1983)
Vigneron, A.: Geometric optimization and sums of algebraic functions. In: Proceedings of the 21st ACM-SIAM Symposium on Discrete Algorithms, pp. 906–917 (2010)
Wetzel, J.: Sectorial covers for curves of constant length. Can. Math. Bull. 16, 367–375 (1973)
Wolff, T.: Recent work connected with the Kakeya problem. In: Rossi, H. (ed.) Prospects in Mathematics. American Mathematical Society, Providence (1999)
Acknowledgements
We thank Helmut Alt, Tetsuo Asano, Jinhee Chun, Dong Hyun Kim, Mira Lee, Yoshio Okamoto, János Pach, Günter Rote, and Micha Sharir for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
H.-K.A. was supported by NRF grant 2011-0030044 (SRC-GAIA) funded by the government of Korea. J.G. is the recipient of an Australian Research Council Future Fellowship (project number FT100100755). S.W. Bae was supported by NRF grant (NRF-2013R1A1A1A05006927) funded by the government of Korea. O.C. was supported in part by NRF grant 2011-0030044 (SRC-GAIA), and in part by NRF grant 2011-0016434, both funded by the government of Korea.
Rights and permissions
About this article
Cite this article
Ahn, HK., Bae, S.W., Cheong, O. et al. A Generalization of the Convex Kakeya Problem. Algorithmica 70, 152–170 (2014). https://doi.org/10.1007/s00453-013-9831-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-013-9831-y