Robust cost function for optimizing chamfer masks

Abstract

Chamfering, a mask-driven technique, refers to a process of propagating local distances over an image to estimate a reference metric. Performance of the technique depends on the design of chamfer masks using cost functions. To date, most scholars have been using a mean absolute error and a mean squared error to formulate optimization problems for estimating weights in the chamfer masks. However, studies have shown that these optimization functions endure some potential weaknesses, including biasedness and sensitivity to outliers. Motivated by the weaknesses, the present work proposes an alternative difference function, RLog, that is unbiased, symmetrical, and robust. RLog takes the absolute logarithm of the relative accuracy of the estimated distance to compute optimal chamfer weights. Also, we have proposed an algorithm to map entries of the designed real-valued chamfer masks into integers. Analytical and experimental results demonstrate that chamfering based on our weights generate polygons and distance maps with lower errors. Methods and results of our work may be useful in robotics to address the matching problem.

Appendices

Appendix 1: Existence of maximum in RLog

Recalling the RLog formula in (2.18), we want to show that $g(\theta )$ contains a global maximum, $g_m$. From the formula, shifted by $+2g(\theta )$ for positivity,

$$\begin{aligned} g'(\theta )=\frac{u\cos \theta -v\sin \theta }{v\cos \theta +u\sin \theta } \end{aligned}$$

(7.1)

and

$$\begin{aligned} g''(\theta )=-\frac{u^2+v^2}{(v\cos \theta +u\sin \theta )^2}\le 0. \end{aligned}$$

(7.2)

Equation 7.2 suggests the existence of a maximum in g. Substituting $g'(\theta )=0$ into (7.1) and solve for $\theta$, we get the location

$$\begin{aligned} \theta _m=\arctan \left( \frac{u}{v}\right) \end{aligned}$$

on the RLog curve that gives the maximum. Substituting $\theta =\theta _m$ into the RLog formula yields the maximum value of

$$\begin{aligned} g_m=\frac{1}{2}\log (u^2+v^2). \end{aligned}$$

(7.3)

Appendix 2: Computation of optimal chamfer weights

For any chamfer mask, optimal weights that control the major error lobe can be computed by considering the conditions $g_m=-g(0^{\circ })$ and $u=(\phi -\varphi )v$, where $\phi$ and $\varphi$ depend on the kernel size (Table 4). Plugging the conditions into the respective formulas gives

$$\begin{aligned} v=\frac{1}{\root 4 \of {(\phi -\varphi )^2+1}}\quad \text { and }\quad u=\frac{\phi -\varphi }{\root 4 \of {(\phi -\varphi )^2+1}}. \end{aligned}$$

(8.1)

Table 4 Values of $\phi$ and $\varphi$ for various kernel sizes

Appendix 3: Detailed derivations of chamfer weights for kernels of order $2n+3$ ($n=1,2,\ldots$)

This Appendix provides further details on how to derive high-order chamfer kernels. For demonstration purposes, we design the local weights for $5\times 5$ and $7\times 7$ kernels.

1.1 $5\times 5$ chamfer mask

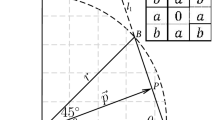
Consider portion of a chamfer polygon, represented by Fig. 4, which contains two sides, namely $\overline{AB}$ and $\overline{BC}$. The polygon is inscribed in a disk of radius r, and our goal is to find the maximum possible errors that each side makes relative to its corresponding arc. For the $5\times 5$ mask, we should compute errors due to $\overline{AB}$ and due to $\overline{BC}$; note that errors are zeros when the sides are (ideally) perfectly aligned with the arcs and , respectively. Adopting notations from the earlier sections, $f_1(\theta )$ and $f_2(\theta )$ correspond to the lengths of $\vec {p}$ from $\overline{AB}$ and from $\overline{BC}$, respectively.

The following items give the systematic procedures to compute optimal errors from each polygon’s side generated by a $5\times 5$ chamfer kernel (refer to Fig. 4 for definitions of variables):

• (a) Use the sine rule to find $f_1(\theta )$ and $f_2(\theta )$:

  $$\begin{aligned} f_1(\theta )=\frac{r\sin \theta _1}{a\sin (\theta +\theta _1)} =\frac{r\sin \theta _1}{a(\sin \theta \cos \theta _1+\cos \theta \sin \theta _1)}. \end{aligned}$$

  (9.1)

  and

  $$\begin{aligned} f_2(\theta )=\frac{r\sin \theta _2}{a\sin (\theta +\theta _2)}=\frac{r\sin \theta _2}{a(\sin \theta \cos \theta _2+\cos \theta \sin \theta _2)}. \end{aligned}$$

  (9.2)

• (b) Use equations of the lines $l_1$ and $l_2$, which, respectively, extend $\overline{AB}$ and $\overline{BC}$, to define $\sin \theta _1$, $\cos \theta _1$, $\sin \theta _2$, and $\cos \theta _2$ in (9.1) and (9.2):

  $$\begin{aligned} \sin \theta _1=\frac{a}{\sqrt{(c-2a)^2+a^2}},~~ \cos \theta _1=\frac{c-2a}{\sqrt{(c-2a)^2+a^2}}; \end{aligned}$$

  (9.3)

  and

  $$\begin{aligned} \sin \theta _2= & {} \frac{c-b}{\sqrt{(2b-c)^2+(c-b)^2}},\nonumber \\ \cos \theta _2= & {} \frac{2b-c}{\sqrt{(2b-c)^2+(c-b)^2}} \end{aligned}$$

  (9.4)

• (c) Substitute (9.3) into (9.1) and (9.4) into (9.2):

  $$\begin{aligned} f_1(\theta )=\frac{r}{(c-2a)\sin \theta +a\cos \theta } \end{aligned}$$

  (9.5)

  and

  $$\begin{aligned} f_2(\theta )=\frac{r}{(2b-c)\sin \theta +(c-b)\cos \theta }. \end{aligned}$$

  (9.6)

• (d) Use the RLog formula to find $g_1(\theta )$ and $g_2(\theta )$, which are the respective errors described by $\vec {p}$ on $\overline{AB}$ and $\overline{BC}$:

  $$\begin{aligned} g_1(\theta )=\log \left( \frac{1}{r}f_1(\theta )\right) =-\log ((c-2a)\sin \theta +a\cos \theta ) \end{aligned}$$

  (9.7)

  and

  $$\begin{aligned} g_2(\theta )= & {} \log \left( \frac{1}{r}f_2(\theta )\right) \nonumber \\= & {} -\log ((2b-c) \sin \theta +(c-b)\cos \theta ). \end{aligned}$$

  (9.8)

• (e) Identify the polygon’s longest side, which corresponds to the edge that produces the maximum RLog value. From Fig. 4,

  $$\begin{aligned} \overline{AB}=\frac{r}{ac}\sqrt{5a^2-4ac+c^2}=r\sqrt{5\left( \frac{a}{c}\right) +\left( \frac{c}{a}\right) -4} \end{aligned}$$

  (9.9)

  and

  $$\begin{aligned} \overline{BC}= & {} \frac{r}{bc}\sqrt{5b^2-6bc+2c^2}\nonumber \\= & {} r\sqrt{5\left( \frac{b}{c}\right) +2\left( \frac{c}{b}\right) -6}. \end{aligned}$$

  (9.10)

  Let $\phi _1=\frac{c}{a}$ and $\phi _2=\frac{c}{b}$. If a, b, and c are selected within the allowable limits, then $\phi _1\ge \phi _2$. Substituting $\phi _1$ into (9.9) and $\phi _2$ into (9.10), we have

  $$\begin{aligned} \overline{AB}=r\sqrt{\frac{5}{\phi _1}+\phi _1-4} \end{aligned}$$

  (9.11)

  and

  $$\begin{aligned} \overline{BC}=r\sqrt{\frac{5}{\phi _2}+2\phi _2-6}. \end{aligned}$$

  (9.12)

  Evidently, $\overline{AB}\ge \overline{BC}$ (a typical test can be done using the Euclidean local weights $a=1$, $b=\sqrt{2}$, and $c=\sqrt{5}$).

• (f) $\overline{AB}\ge \overline{BC}$ implies that $g_{1m}\ge g_{2m}$, where $g_{1m}$ and $g_{2m}$ are the respective peaks for the curves $g_{1}$ and $g_{2}$. One strategy to minimize $g_{1m}$ is to push $\overline{AB}$ outward in the direction of $\vec {p}$ such that a triangle extended from $\triangle OAB$ is isosceles, or $c=\sqrt{5}a$ and $-g_1(0^{\circ })=g_{1m}$. Solving the equations gives $a_{\mathrm {opt}}=0.9865$ and $c_{\mathrm {opt}}=2.2059$. The value of b should be chosen such that the maximum RLog stays in the range $0\le g_1(\theta )\le g_{1m}$, and a natural choice is the Euclidean value $b=\sqrt{2}$.

1.2 $7\times 7$ chamfer mask

We use Fig. 7 to optimize the local weights in the $7\times 7$ chamfer mask. Following similar strategies as those used in the case of the $5\times 5$ mask, the steps are itemized below:

• (a) The derived lengths of $\vec {p}$ on $\overline{AB}$, $\overline{BC}$, $\overline{CD}$, and $\overline{DE}$ are, respectively,

  $$\begin{aligned} f_1(\theta )= & {} \frac{r\sin \theta _1}{a\sin (\theta +\theta _1)}= \frac{r\sin \theta _1}{a(\sin \theta \cos \theta _1+\cos \theta \sin \theta _1)}, \end{aligned}$$

  (9.13)
  $$\begin{aligned} f_2(\theta )= & {} \frac{r\sin \theta _2}{a\sin (\theta +\theta _2)}= \frac{r\sin \theta _2}{a(\sin \theta \cos \theta _2+\cos \theta \sin \theta _2)}, \end{aligned}$$

  (9.14)
  $$\begin{aligned} f_3(\theta )= & {} \frac{r\sin \theta _3}{a\sin (\theta +\theta _3)}=\frac{r\sin \theta _3}{a(\sin \theta \cos \theta _3+\cos \theta \sin \theta _3)},\nonumber \\ \end{aligned}$$

  (9.15)

  and

  $$\begin{aligned} f_4(\theta )=\frac{r\sin \theta _4}{a\sin (\theta +\theta _4)}=\frac{r\sin \theta _4}{a(\sin \theta \cos \theta _4+\cos \theta \sin \theta _4)}. \end{aligned}$$

  (9.16)

• (b) The trigonometric functions with respect to $\theta _i$ ($i=1,2,3,$ and 4) are

  $$\begin{aligned} \sin \theta _1= & {} \frac{a}{\sqrt{(d-3a)^2+a^2}}, \end{aligned}$$

  (9.17)
  $$\begin{aligned} \cos \theta _1= & {} \frac{d-3a}{\sqrt{(d-3a)^2+a^2}}, \end{aligned}$$

  (9.18)
  $$\begin{aligned} \sin \theta _2= & {} \frac{d-c}{\sqrt{(3c-2d)^2+(d-c)^2}}, \end{aligned}$$

  (9.19)
  $$\begin{aligned} \cos \theta _2= & {} \frac{3c-2d}{\sqrt{(3c-2d)^2+(d-c)^2}}, \end{aligned}$$

  (9.20)
  $$\begin{aligned} \sin \theta _3= & {} \frac{2c-e}{\sqrt{(2e-3c)^2+(2c-e)^2}}, \end{aligned}$$

  (9.21)
  $$\begin{aligned} \cos \theta _3= & {} \frac{2e-3c}{\sqrt{(2e-3c)^2+(2c-e)^2}}, \end{aligned}$$

  (9.22)
  $$\begin{aligned} \sin \theta _4= & {} \frac{e-2b}{\sqrt{(3b-e)^2+(e-2b)^2}}, \end{aligned}$$

  (9.23)

  and

  $$\begin{aligned} \cos \theta _4=\frac{3b-e}{\sqrt{(3b-e)^2+(e-2b)^2}}. \end{aligned}$$

  (9.24)

• (c) Substitutions of ${\sin \theta _{i}}'s$ and ${\cos \theta _{i}}'s$ into the respective equations for ${f_{i}}'s$ ($i=1,2,3$ and 4) yield

  $$\begin{aligned} f_1(\theta )= & {} \frac{r}{(d-3a)\sin \theta +a\cos \theta }, \end{aligned}$$

  (9.25)
  $$\begin{aligned} f_2(\theta )= & {} \frac{r}{(3c-2d)\sin \theta +(d-c)\cos \theta }, \end{aligned}$$

  (9.26)
  $$\begin{aligned} f_3(\theta )= & {} \frac{r}{(2e-3c)\sin \theta +(2c-e)\cos \theta }, \end{aligned}$$

  (9.27)

  and

  $$\begin{aligned} f_4(\theta )=\frac{r}{(3b-e)\sin \theta +(e-2b)\cos \theta }. \end{aligned}$$

  (9.28)

• (d) The corresponding RLog formulae are

  $$\begin{aligned} \overline{AB}:~g_1(\theta )= & {} \log \left( \frac{1}{r}f_1(\theta )\right) = -\log ((d-3a)\sin \theta \nonumber \\&+a\cos \theta ), \end{aligned}$$

  (9.29)
  $$\begin{aligned} \overline{BC}:~g_2(\theta )= & {} \log \left( \frac{1}{r}f_2(\theta )\right) = -\log ((3c-2d)\sin \theta \nonumber \\&+(d-c)\cos \theta ), \end{aligned}$$

  (9.30)
  $$\begin{aligned} \overline{CD}:~g_3(\theta )= & {} \log \left( \frac{1}{r}f_3(\theta )\right) = -\log ((2e-3c)\sin \theta \nonumber \\&+(2c-e)\cos \theta ), \end{aligned}$$

  (9.31)

  and

  $$\begin{aligned} \overline{DE}:~g_4(\theta )= & {} \log \left( \frac{1}{r}f_4(\theta )\right) =-\log ((3b-e)\sin \theta \nonumber \\&+(e-2b)\cos \theta ). \end{aligned}$$

  (9.32)

• (e) Comparing the RLog formulae, $g_1(\theta )$ contains the maximum possible error of $g_{1m}=-\frac{1}{2}\log ((d-3a)^2+a^2)$, suggesting that $\overline{AB}$ is the longest side.

• (f) Considering the optimality conditions for $\triangle OAB$, we solve the equations $d=\sqrt{10}a$ and $-g_1(0^{\circ })=g_{1m}$. Therefore, the optimal local weights for the $7\times 7$ chamfer mask are $a_{\mathrm {opt}}=0.9935$ and $d_{\mathrm {opt}}=3.1418$. The remaining non-redundant weights should be carefully selected on the condition that RLog on either error lobe stays within the bounds dictated by $g_{1m}$. And, an obvious selection is the Euclidean local weights $b=\sqrt{2}$, $c=\sqrt{5}$, and $e=\sqrt{13}$.