1 Introduction

Network design is among the most well-studied problems in the combinatorial optimization literature. A natural definition is as follows. We are given a graph consisting of a set of nodes and edges among them representing potential links. Each edge has an associated cost which corresponds to the cost for establishing the corresponding link. We are also given connectivity requirements as pairs of source-destination nodes. The objective is to compute a subgraph of the original graph of minimum total cost that satisfies the connectivity requirements. In other words, we seek to establish a network that satisfies the connectivity requirements at the minimum cost. This optimization problem is known as Minimum Steiner Forest and generalizes well-studied problems such as the Minimum Spanning Tree and Minimum Steiner Tree.

In this paper, we consider a game-theoretic variant of network design that was first considered in [2]. Instead of considering the connectivity requirements as a global goal, we assume that each connectivity requirement is desirable by a different player. The players participate in a non-cooperative game; each of them selects as her strategy a path from her source to the destination and is charged for part of the cost of the edges she uses. According to the fair cost sharing scheme we consider in the current paper, the cost of an edge is shared equally among the players using the edge. The social cost of an assignment (i.e., a snapshot of players’ strategies) is the cost of the edges contained in at least one path. An optimal assignment would contain a set of edges of minimum cost so that the connectivity requirements of the players are satisfied. Unfortunately, this does not necessarily mean that all players are satisfied with this assignment since a player may have an incentive to deviate from her path to another one so that her individual cost is smaller. Eventually, the players will reach a set of strategies (and a corresponding network) that satisfies their connectivity requirements and in which no player has any incentive to deviate to another path; such outcomes are known as Nash equilibria. Interestingly, even though the optimal solution is always a forest, Nash equilibria may contain cycles.

The non-optimality of the outcomes of network design games (which is typical when selfish behavior comes into play) leads to the following question that has been a main line of research in Algorithmic Game Theory: How is the system performance affected by selfish behavior? The notion of the price of anarchy (introduced in the seminal paper of Koutsoupias and Papadimitriou [8]; see also [10]) quantifies the deterioration of performance. In general terms, it is defined as the ratio of the social cost of the worst possible Nash equilibrium over the optimal cost. Hence, it is pessimistic in nature and (as its name suggests) provides a worst-case guarantee for conditions of total anarchy. Instead, the notion of the price of stability that was introduced in the paper of Anshelevich et al. [2] is optimistic in nature. It is defined as the ratio of the social cost of the best equilibrium over the optimal cost and essentially asks: What is the best one can hope for the system performance given that the players are selfish?

The aim of the current paper is to determine better lower bounds on the price of stability for network design games in an attempt to understand the effect of selfishness on the efficiency of outcomes in such games. We usually refer to network design games as multi-source network design games in order to capture the most general case in which players may have different sources. An interesting variant is when each player wishes to connect a particular common node, which we call the root, with her destination node; we refer to such network design games as multicast games. An interesting special case of multicast games is the class of broadcast games: in such games, there is a player for each non-root node of the network that has this node as her destination.

Related Work

The existence of Nash equilibria in network design games is guaranteed by a potential function argument. Rosenthal [11] defined a potential function over all assignments of a network design game so that the difference in the potential of two assignments that differ in the strategy of a single player equals the difference of the cost of that player in these assignments; hence, an assignment that locally minimizes the potential function is a Nash equilibrium. So, the price of stability is well-defined in network design games. Anshelevich et al. [2] considered network design games in directed graphs and proved that the price of stability is at most H n . Their proof considers a Nash equilibrium that can be reached from an optimal assignment when the players make arbitrary selfish moves. The main argument used is that the potential of the Nash equilibrium is strictly smaller than that of the optimal assignment and the proof follows due to the fact that the potential function of Rosenthal approximates the social cost of an assignment within a factor of at most H n . This approach suggests a general technique for bounding the price of stability and has been extended to other games as well; see [3, 5]. For directed graphs, the bound of H n was also proved to be tight [2]. Although the upper bound proof carries over to undirected network design games, the lower bound does not. The bound of H n is the only known upper bound for multi-source network design games in undirected graphs. Better upper bounds are known for single-source games. For broadcast games, Fiat et al. [7] proved an upper bound of O(loglogn) while Li [9] presented an upper bound of O(logn/loglogn) for multicast games. These bounds are not known to be tight either and, actually, the gap with the corresponding lower bounds is large. For single-source games, in the full version of [7] Fiat et al. present a lower bound of 12/7≈1.714; their construction uses a broadcast game. This was the best lower bound known for the multi-source case as well until the recent work of Christodoulou et al. [6] who presented an improved lower bound of 42/23≈1.826. Higher (i.e., super-constant) lower bounds are only known for weighted variants of network design games (see [1, 4]).

Our Results

In this paper, we present better lower bounds for general undirected network design games, as well as for the restricted variants of broadcast and multicast games. For the general case, we present a game that has price of stability at least 348/155≈2.245, improving the previously best known lower bound of [6]. Our proof uses a simple gadget as the main building block which is augmented by a recursive construction to our lower bound instance. The particular recursive construction of the game has two advantages. Essentially, the recursive construction blows up the price of stability of the gadget used as the main building block. Furthermore, recursion allows to handle successfully the technical difficulties in the analysis. We believe that our construction could be extended to use more complicated gadgets as building blocks that would probably lead to better lower bounds on the price of stability (at the expense of significantly more complicated proofs compared to our current one). For multicast games, we present a lower bound of 1.862. Our proof uses a game on a graph with a particular structure. For this game, we prove sufficient conditions on the edge costs of the graph so that a particular assignment is the unique Nash equilibrium. Then, the construction that yields the lower bound is the solution of a linear program which has the edge costs as variables, the sufficient conditions as constraints, an additional constraint that upper-bounds the optimal cost by 1, and its objective is to maximize the cost of the unique Nash equilibrium. The particular lower bound was obtained in a game with 100 players using the linear programming solver of Matlab. A slight variation of this construction yields our lower bound of 1.818 for broadcast games. In this case, we are able to obtain a more compact set of sufficient conditions so that there is a unique Nash equilibrium. As a result, we present a formal proof that the price of stability approaches 20/11≈1.818 when the number of players is large.

We remark that proving lower bounds on the price of stability is significantly more difficult for undirected network design games compared to their directed counterparts. This is due to the fact that edges are not constrained to be used in a single direction and, hence, the strategy space of each player is much larger. In order to prove high lower bounds, one must construct a game on an undirected graph in which any Nash equilibrium is much different than the optimal solution. Usually (this applies to all previous proofs as well as to the ones in the current paper), such lower bound constructions have a unique Nash equilibrium. Achieving simultaneously uniqueness (among many different possible assignments) and high cost of a Nash equilibrium is the most difficult part of our proofs.

Roadmap

The rest of the paper is structured as follows. We begin with preliminary definitions in Sect. 2. Section 3 is devoted to the proof of the lower bound for multi-source undirected network design games. Our lower bounds for broadcast and multicast games appear in Sect. 4. We conclude in Sect. 5.

2 Preliminaries

In an undirected network design game, we are given an undirected graph G=(V,E) in which each edge e∈E has a non-negative cost c e . There are n players; player i wishes to establish a connection between two nodes s i ,t i ∈V called the source and destination node of player i, respectively. The set of strategies available to player i consists of all paths connecting nodes s i and t i in G. We call an assignment any set of strategies σ, with one strategy per player. Given an assignment σ, let n e (σ) be the number of players using edge e in σ. Then, the cost of player i in σ is defined as \(\mbox{cost}_{i}(\sigma) = \sum_{e\in\sigma_{i}}\frac{c_{e}}{n_{e}(\sigma)}\), where σ i denotes the strategy of player i in σ. Let G(σ) be the subgraph of G which contains the edges of G that are used by at least one of the players in assignment σ. Given a subset of players P, we also denote by G(σ P ) the subgraph of G which contains the edges of G that are used by at least one of the players in P in assignment σ. The social cost of the assignment σ is simply the total cost of the edges in G(σ) which coincides with the sum of the costs of the players.

An assignment σ is called a Nash equilibrium if for any player i and for any other assignment σ′ that differs from σ only in the strategy of player i, it is cost i (σ)≤cost i (σ′). The price of stability of a network design game is defined as the ratio of the minimum social cost among all Nash equilibria over the optimal cost.

Network design games with s i =s for any player i are called multicast games. We refer to node s as the root node. Multicast games in which there is one player for any non-root node that has this node as destination are called broadcast games. We also use the term multi-source games to refer to the general class of undirected network design games and the term single-source games in order to refer to multicast and broadcast games.

In the following, we specifically consider network design games in which the cost of each edge is strictly positive. In such a game, an assignment σ is called proper if, for every pair of players i,j, the graph G(σ {i,j}) is acyclic. This definition implies that, in a proper assignment, all players follow simple paths and, furthermore, if two players i and j both contain two different nodes c 1 and c 2 in their strategies, then the subpaths they use in order to connect nodes c 1 and c 2 are identical. It can be easily seen that any Nash equilibrium is a proper assignment; for the sake of completeness, we include the proof of this statement here.

Claim 1

Any Nash equilibrium is a proper assignment.

Proof

Consider a network design game and a Nash equilibrium σ. We will show that σ is proper. Clearly, if there was a player i with a non-simple path as a strategy, she could improve her cost by short-cutting her path. Assume now that there are two players i and j whose strategies in σ include two nodes c 1 and c 2. Let C i (respectively, C j ) be the set of edges in the subpath in the strategy of player i (respectively, j) that connects nodes c 1 and c 2. We will show that C i =C j .

Assume for the sake of contradiction that \((C_{i}\setminus C_{j}) \cup(C_{j} \setminus C_{i})\not=\emptyset\). Without loss of generality, assume that \(\sum_{e\in C_{i}\setminus C_{j}}{\frac{c_{e}}{n_{e}(\sigma)}} \leq\sum_{e\in C_{j}\setminus C_{i}}{\frac{c_{e}}{n_{e}(\sigma)}}\) (the other case is completely symmetric). Consider the deviation of player j that replaces the edges of C j ∖C i with the edges of C i ∖C j and denote the new assignment by σ′. Note that n e (σ′)=n e (σ) for each edge \(e\in\sigma'_{j}\setminus (C_{i}\setminus C_{j})\) (i.e., for each edge e∈σ j ∖(C j ∖C i )) and n e (σ′)=n e (σ)+1 for each edge e∈C i ∖C j . Hence, the difference in the cost of player j in both assignments is

and, equivalently, cost j (σ)′<cost j (σ). This contradicts the fact that the assignment σ is a Nash equilibrium and the claim follows. □

3 The Lower Bound for Multi-Source Games

In this section, we prove the following theorem.

Theorem 2

For any δ>0, there exists an undirected network design game with price of stability at least 348/155−δ.

We will construct a network design game on a connected undirected graph so that there is a distinct player associated with each edge of the graph that wishes to connect the endpoints of the edge. The construction is such that there is a unique Nash equilibrium in which each player uses her direct edge.

The construction uses integer parameters k≥3 and t≥2. We start with the gadget construction depicted in Fig. 1a. We use the terms left and right gadget player for the players associated with the left and right gadget edge of a gadget, respectively. We also use the term floor players for the players associated with floor edges.

Fig. 1
figure 1

(a) The gadget used in the proof of Theorem 2. (b) The construction of a block under a ceiling edge (with k=3)

Full size image

Given an edge e, we build a block under this edge by putting k gadgets so that the leftmost node of the first gadget coincides with the left endpoint of e, the rightmost node of i-th gadget coincides with the leftmost node of the (i+1)-th gadget for i=1,…,k−1, and the rightmost node of the k-th gadget coincides with the right endpoint of e (see Fig. 1b). We refer to e as the ceiling edge of the block.

In order to define the cost of the edges in our construction, we use positive parameters x, y, z, w, and α (to be fixed in a while). If g denotes the cost of the ceiling edge, then the cost of the edges in each gadget of the block under it are defined as follows:

  • \(\frac{xg}{\alpha k^{2}}\) for each of the left floor edges,

  • \(\frac{(1-x-y)g}{\alpha k^{2}}\) for each of the middle floor edges,

  • \(\frac{yg}{\alpha k^{2}}\) for each of the right floor edges,

  • \(\frac{zg}{\alpha k}\) for the left gadget edge, and

  • \(\frac{wg}{\alpha k}\) for the right gadget edge.

So, the total cost of the floor edges of the block is g/α while the total cost of all edges of the block is g(1+z+w)/α.

Now, our construction starts with a roof edge of cost 1 (and an associated roof player) and a block under it. The roof edge has level t and the block under it has level t−1. We build blocks of level t−2 by building a block under each of the floor edges of the block of level t−1. We continue recursively and define all blocks down to level 1. Clearly, for j=1,…,t−1, the total cost of the floor edges of level j is gα j−t while the total cost of all edges of level j is g(1+z+w)α j−t.

We now fix the values of the parameters as follows. We set x=28/109, y=33/109, z=30/109−ϵ, w=35/109−ϵ, and α=63/218−ϵ, where ϵ is a negligibly small but strictly positive number. Hence, the total cost of the edges in the graph is

while the cost of the floor edges of level 1 is α 1−t and upper-bounds the optimal cost (since the floor edges of level one constitute a spanning tree of the whole graph). For any δ>0, we can set t and ϵ appropriately so that the ratio of the total cost of edges over the optimal cost is at least 348/155−δ.

In order to complete the proof of the theorem, it suffices to prove that the assignment in which each player uses her direct edge is the unique Nash equilibrium; the rest of this section is devoted to proving this claim. We begin with some definitions.

We will refer to the players associated to floor edges (respectively, gadget edges) at blocks of level j as the floor players of level j (respectively, the gadget players of level j). A floor player of level j follows a non-increasing strategy if she uses neither a gadget edge of her gadget nor any edge of level j′>j. A gadget player of level j follows a non-increasing strategy if she does not use any edge of level j′>j. In the opposite case, we say that the player follows an increasing strategy.

In an assignment, a player may use a floor edge or connect her endpoints by being routed through the block under the edge. In the latter case, we say that the player crosses the floor edge. We also say that a player is external to a gadget (respectively, external to a block) if she does not correspond to any edge of the gadget (respectively, block) and uses or crosses its edges.

Recall that our goal is to prove that no assignment besides the one in which each player uses her direct edge is a Nash equilibrium. In order to do so, by Claim 1, we have to consider only proper assignments. In a proper assignment, the sets of non-increasing strategies of the gadget players of a gadget can belong to one of the following types (see Fig. 2):

  • Type A: Both gadget players use their direct edges.

  • Type B: The left gadget player uses her direct edge and the right gadget player uses or crosses the middle and right floor edges.

  • Type C: Both gadget players use the left gadget edge. The right gadget player uses or crosses the left and right floor edges as well.

  • Type D: The right gadget player uses her direct edge and the left gadget player uses or crosses the left and middle floor edges.

  • Type E: Both gadget players use the right gadget edge. The left gadget player uses or crosses the left and right floor edges as well.

  • Type F: The left gadget player uses or crosses the left and middle floor edges and the right gadget player uses or crosses the middle and right floor edges.

Any other set of non-increasing strategies violates the fact that the assignment is proper. Indeed, one such example is the assignment in which the left gadget player uses or crosses the left and middle floor edges and the right gadget player uses or crosses the left and right floor edges. Here, the edges used by the left gadget player form a cycle together with the left gadget edge used by the right gadget player.

Fig. 2
figure 2

The six possible types for the players of a gadget that follow non-increasing strategies. The dashed lines denote the paths used by the left and the right gadget player. Only the gadget edges that are used by some player are shown

Full size image

We are ready to significantly restrict the structure of assignments we have to consider as candidates to be Nash equilibria.

Lemma 3

At any Nash equilibrium, all (non-roof) players follow non-increasing strategies. Furthermore, at each block:

  • either there are no external players and the gadget players have strategies of type A

  • or there are h>0 external players and each of them experiences cost more than g/h, where g is the cost of the ceiling edge of the block.

Proof

Consider a Nash equilibrium. We will prove the claim inductively (on the block level). We will first prove it for the blocks of level 1. In this case, there is no block under any floor edge and players do not cross the floor edges.

Consider a block of level 1 and assume that a floor player p follows an increasing strategy. This means that she uses a strategy that includes either a gadget edge of her gadget or an edge of level higher than 1. In both cases, our construction guarantees that player p should use the k−1 floor edges that connect the endpoints of her edge to the two closest nodes that are gadget edge endpoints. Furthermore, observe that neither a gadget player of the same gadget nor an external player to this gadget uses these floor edges (since this would imply that they also use the direct edge of player p and the assignment would not be proper). Similarly, the players associated to the k−1 floor edges use their direct edges as strategies. Hence, player p uses each of the k−1 floor edges together with one floor player. Since k≥3, this means that the cost she experiences at the k−1≥2 floor edges plus the non-zero cost she experiences at the other edges she uses is strictly larger than the cost of her direct edge and she would have an incentive to move to her direct edge. So, all floor players of the block follow non-increasing strategies.

Now, assume that a gadget player p follows an increasing strategy, i.e., her path contains the endpoints of her gadget. This means that there are no external players to the current block neither other gadget players within the current block that follow increasing strategies (any such player should connect the endpoints of the gadget of p and the assignment would not be proper). So far, we have proved that every player in the current block besides p follows a non-increasing strategy. Our next step is to prove that p cannot follow an increasing strategy either. In order to do so, we will first focus on a gadget of the current block whose players follow non-increasing strategies (the above argument implies that there are at least k−1 such gadgets) and reason about the strategies of the gadget players and the number of external players.

Let us focus on a gadget of the current block whose players follow non-decreasing strategies and assume that there are h≥0 external players; these can be players that are external to the block or a player from another gadget of the same block that follows an increasing strategy. In the inequalities below, we use the following easy claim.

Claim 4

Let ζ,η be positive integers. Then, \(\frac{1}{\zeta+h} \geq \frac{\eta}{(\zeta+\eta) h}\) for any integer h≥η.

We consider the six different cases for the strategies of the gadget players. If the strategies of the gadget players are of type A, then all the external players (if any) are routed either through the left gadget edge and the right floor edges of the gadget, or through the left floor edges and the right gadget edge, or through the left gadget edge, the middle floor edges, and the right gadget edge (in any other case, the strategy of the external player would form a cycle with the strategy of a gadget player; this would violate the fact that the assignment is proper). In the first subcase, the cost of each external player at the edges of the gadget is

In the second subcase, the cost of each external player is

In the third subcase, the cost of each external player is

If the strategies of the gadget players are of type B, all the external players are routed through the left gadget edge and the right floor edges. We will first show that h≥2. Indeed, if at most one external player is routed through the gadget, the cost of the right gadget player would be at least

i.e., this player would have an incentive to move and use her direct edge. So, since h≥2, the cost of each external player at the edges of the gadget is

If the strategies of the gadget players are of type C, all the external players are routed through the left gadget edge and the right floor edges. We will show again that h≥2. Indeed, if at most one external player is routed through the gadget, the cost of the right gadget player would be at least

i.e., this player would have an incentive to move. So, since h≥2, the cost of each external player at the edges of the gadget is

If the strategies of the gadget players are of type D, all the external players are routed through the left floor edges and the right gadget edge. We will show again that h≥2. Indeed, if at most one external player is routed through the gadget, the cost of the left gadget player would be at least

i.e., this player would have an incentive to move. So, since h≥2, the cost of each external player at the edges of the gadget is

If the strategies of the gadget players are of type E, then all the external players are routed through the left floor edges and the right gadget edge. We will show again that h≥2. Indeed, if at most one external player is routed through the gadget, the cost of the left gadget player would be at least

i.e., this player would have an incentive to move. So, since h≥2, the cost of each external player at the edges of the gadget is

If the strategies of the gadget players are of type F, then all the external players are routed through the floor edges. We will show that h>0 in this case. Indeed, if there were no external players that are routed through the gadget, the cost of the left gadget player would be

i.e., this player would have an incentive to move. So, the cost of each external player at the edges of the gadget is

Now, consider again the gadget player p for which we have assumed that she may follow an increasing strategy. As we observed above, player p is the only external player in each of the remaining k−1 gadgets of the current block. In each of these gadgets, the gadget players have strategies of types A or F; this follows since, in the above analysis, these are the only cases for which the number h of external players can be 1 and the gadget players do not have an incentive to deviate. Furthermore, our analysis yields that the cost player p experiences at the edges of the gadget is more than \(\frac {g}{k}\). Her total cost through the edges of the k−1≥2 gadgets different than her own one would be \(\frac{g(k-1)}{k} \geq\frac{g}{\alpha k}\max\{z,w\}\), i.e., she would have an incentive to move and use her direct edge instead. So, all gadget players of the block follow non-increasing strategies as well.

Now, assume that no external player is routed through the block. Then, by the above discussion, the only case in which the gadget players of a gadget do not have an incentive to move is when they follow strategies of type A. If one external player is routed through the block, then the gadget players follow strategies of type A or F and the cost experienced by the external player at each gadget is more than g/k, i.e., more than g in total. If h≥2 external players are routed through the block, then each of them experiences cost more than \(\frac {g}{k h}\) at each gadget, i.e., more than g/h in total.

We have completed the proof of the base of the induction. Now, assuming that the statement is true for blocks of levels up to j, we have to prove it for blocks of level j+1. The proof of the induction step is almost identical to the proof of the induction base. The only difference is that, now, a player may cross a floor edge in order to connect its endpoints. Then, when h players cross a floor edge, they are external to the block under the edge and (by the induction hypothesis) the cost they experience when crossing the edge is more than its cost over h (as opposed to exactly its cost over h which we had in the induction base). This inequality (instead of equality) does not affect any of the inequalities above and the proof of the induction step completes in the very same way. □

Lemma 5

At any Nash equilibrium, there are no external players at any block.

Proof

For the sake of contradiction, assume that this is not the case and consider a Nash equilibrium with external players at some block. Consider a block B of highest level that has some external player routed through it. We will first show that at most one player is routed through B. We distinguish between two cases:

  • Block B is the block of level t−1 under the roof edge. Since all players follow non-increasing strategies, the only player that may go through block B is the roof player.

  • The block B is at level j (with 1≤j<t−1). Let e be its ceiling edge; this is a floor edge of a gadget Γ at level j+1. By our assumption, Γ has no external players. Furthermore, by Lemma 3, the gadget players of Γ follow strategies of type A (i.e., their direct gadget edges) and any other player follows a non-increasing strategy. Hence, the only player that may cross edge e and go through block B is the floor player associated with edge e.

So, in both cases, exactly one external player is routed through block B. Furthermore, by Lemma 3, her cost at the edges of block B is more than the cost of e. Hence, this player has an incentive to move and use edge e instead. The lemma follows. □

By Lemmas 3 and 5 we conclude that the assignment in which every player uses her direct edge is the unique Nash equilibrium. This completes the proof of Theorem 2.

4 Lower Bounds for Single-Source Games

In this section, we present our lower bounds for multicast and broadcast games. We note that since all players have a common source node in such games, in any proper assignment the set of edges that are used by at least one player is a tree that is rooted at the source node and spans the destinations of all players. Also, any such tree defines in a unique way the strategies of the players in a proper assignment. So, when considering Nash equilibria in multicast or broadcast games, it suffices to restrict our attention to assignments defined by trees spanning the root node and the destination nodes of all players. We refer to them as multicast or broadcast trees depending on whether the game is a multicast or a broadcast game.

4.1 Multicast Games

Our lower bound for multicast games uses the graph M n depicted at the left part of Fig. 3. There are n players; player i wishes to connect node s to node t i . The cost of the edges is defined by the tuple C=(x 2,…,x n ,y 1,…,y n ,z 1,…,z n ) with positive entries. We denote by τ the multicast tree formed by the edges (s,t i ) for i=1,…,n. The next lemma provides a sufficient condition so that the assignment defined by tree τ is the unique Nash equilibrium of the multicast game on M n . Essentially, it provides sufficient conditions for the cost of the edges of M n such that, in any proper assignment different than τ, some player has an incentive to change her strategy.

Fig. 3
figure 3

The graphs M n (left) and B n (right)

Full size image

Lemma 6

The assignment defined by tree τ is the unique Nash equilibrium of the multicast game on graph M n if C is such that

  1. 1.

    for i=2,…,n and for k=1,…,i−1 it holds:

    $$z_k<\frac{z_i}{\min\{2i-2k,n-k\}+1}+\frac{y_i}{\min\{2i-2k,n-k\}}+\sum _{p=0}^{i-k-1}\frac{x_{i-p}}{i-k-p}+y_k, $$
  2. 2.

    and for i=1,…,n−1 and for j=i+1,…,n it holds

    $$z_j<\frac{z_i}{\min\{2j-2i,j\}}+\frac{y_i}{\min\{2j-2i,j\}-1}+\sum _{p=1}^{j-i}\frac{x_{i+p}}{j-i-p+1}+y_j. $$

Proof

Consider a proper assignment in which the edge (s,t q ) is used by more than one players and denote by left and right the leftmost and rightmost player that use it. Clearly, left≥1, right≤n, left≤q≤right and at least one of left and right is different than q. We will show that one of the players left and right has an incentive to change her strategy. We distinguish between two cases.

Case 1. left+right≤2q. Together with the inequality right≤n, this implies that right−left≤min{2q−2left,n−left}.

Since right≥q and one of left and right is different than q, it must be left<q in this case. So, player left uses the edge (s,t q ) together with some of the right−left players left+1,…,right, the edge (t q ,v q ) together with some of the right−left−1 players left+1,…,q−1,q+1,…,right, the edge (v q−p−1,v q−p ) together with some of the q−left−p−1 players left+1,…,q−p−1 for p=0,…,q−left−2, and the edges (v left ,v left+1) and (t left ,v left ) alone. Her cost is at least

i.e., player \(\sf left\) has an incentive to move and use the edge (s,t left ) instead. The second inequality follows by applying the condition 1 with i=q and k=left.

Case 2. left+right≥2q+1. Together with the inequality left≥1, this implies that right−left≤min{2right−2q,right}−1.

Since left≤q, it is right>q in this case. So, player right uses the edge (s,t q ) together with some of the right−left players left,left+1,…,right−1, the edge (t q ,v q ) together with some of the right−left−1 players left,…,q−1,q+1,…,right−1, the edge (v q+p−1,v q+p ) together with some of the right−q−p players q+p,…,right−1 for p=1,…,right−q−1, and the edges (v right−1,v right ) and (t right ,v right ) alone. Her cost is at least

i.e., player \(\sf right\) has an incentive to move and use the edge (s,t right ) instead. The second inequality follows by applying the condition 2 with i=q and j=right. □

Now, we can use Lemma 6 to obtain lower bounds on the price of stability of multicast games by solving the following linear program. The variables of the linear program are the edge costs of the tuple C. The objective is to maximize the cost \(\sum_{i=1}^{n}{z_{i}}\) of tree τ subject to the two sets of constraints in the statement of Lemma 6 and the additional constraint \(z_{1}+\sum_{i=2}^{n} x_{i} +\sum_{i=1}^{n} y_{i}\leq1\) which upper-bounds the optimal cost by 1 (observe that the left-hand side of this constraint is the cost of the multicast tree containing all edges of M n besides (s,t i ) for i=2,…,n). Then, the objective value of this linear program is a lower bound on the price of stability of the multicast game on M n for the particular values of the edge costs that correspond to the solution of the linear program. Table 1 contains the lower bounds on the price of stability obtained by using the linear programming solver of Matlab. Note that we have simulated the strict inequalities in the conditions of Lemma 6 by using standard inequalities and adding a constant of 10−6 on their left-hand side. The following statement summarizes our best observed lower bound.

Table 1 Lower bounds on the price of stability of the multicast and broadcast games on graphs M n and B n for specific values of n
Full size table

Theorem 7

There exists a multicast game with price of stability at least 1.862.

4.2 Broadcast Games

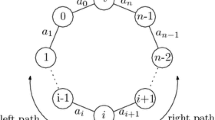
Our lower bound for broadcast games uses the graph B n depicted at the right part of Fig. 3. In this case, the cost of the edges is defined by the tuple C=(x 2,…,x n ,z 1,…,z n ) with positive entries. Again, there are n players; player i wishes to connect node s to node t i . Denote by τ the broadcast tree formed by the edges (s,t i ) for i=1,…,n.

Observe that the graph B n is obtained from M n by contracting the edges (t i ,v i ). Hence, any Nash equilibrium of the multicast game on graph M n with y i =0 for i=1,…,n corresponds to a Nash equilibrium of the broadcast game on graph B n of the same cost (and vice versa) while the cost of the optimal assignment is the same in both cases. So, we can apply the same technique we used above by further constraining the variable y i to be zero for i=1,…,n. In this way, we obtain the bounds on the price of stability shown in Table 1 for values of n up to 100.

Fortunately, we are able to define a much more compact set of conditions for C in order to guarantee that the assignment defined by τ is the unique Nash equilibrium of the broadcast game on B n . This is done in Lemma 8; then, for any n, we explicitly set the values of C and prove analytically our lower bound of 20/11 on the price of stability of broadcast games with many players (in Theorem 9).

Lemma 8

If C is such that

  1. 1.

    x i >z i−1−z i /3 for i=2,…,n−1,

  2. 2.

    x i+1>z i+1−z i /2 for i=1,…,n−1, and

  3. 3.

    x n >z n−1−z n /2,

then the assignment defined by tree τ is the unique Nash equilibrium of the broadcast game on graph B n .

Proof

Consider a proper assignment in which the edge (s,t q ) is used by more than one player and denote by left and right the number of players that use edge (s,t q ) that have indices smaller and larger than q, respectively. Since the assignment is proper, these players should be q−left,q−left+1,…,q+right. We will show that some of these players has an incentive to change her strategy. We distinguish between three cases:

Case 1. left=0 and right>0. In this case, player q+right uses edge (s,t q ) together with the right players q,q+1,…,q+right−1, edge (t q+i−1,t q+i ) together with the right−i players q+i,…,q+right−1 for i=1,…,right−1, and edge (t q+right−1,t q+right ) alone. Using condition 2, we have that the cost of player q+right is

(1)

i.e., player q+right has an incentive to change her strategy and use edge (s,t q+right ) instead.

Case 2. left>0 and right=0. In this case, player q−left uses edge (s,t q ) together with the left players q−left+1,…,q, edge (t q−i ,t q−i+1) together with the left−i players q−left+1,…,q−i for i=1,…,left−1, and edge (t q−left ,t q−left+1) alone. Observe that conditions 1 and 3 imply that x i >z i−1−z i /2 for i=2,…,n. Then, we have that the cost of player q−left is

i.e., player q−left has an incentive to change her strategy and use edge (s,t q−left ) instead.

Case 3. left>0 and right>0. In this case, player q+right uses edge (s,t q ) together with the left+right players q−left,…,q+right−1, edge (t q+i−1,t q+i ) together with the right−i players q+i,…,q+right−1 for i=1,…,right−1, and edge (t q+right−1,t q+right ) alone. Assume that player q+right has no incentive to change her strategy to (s,t q+right ), i.e., her cost is not larger than z q+right . Then, we can use (1) to obtain

which implies that right<left+1 and, hence, right≤left since left and right are integers.

Player q−left uses edge (s,t q ) together with the right+left players q−left+1,…,q+right, edge (t q−i ,t q−i+1) together with the left−i players q−left+1,…,q−i for i=1,…,left−1, and edge (t q−left ,t q−left+1) alone. Now assume that neither player q−left has an incentive to change her strategy to (s,t q−left ), i.e., her cost is not larger than z q−left . Then, using this fact and condition 2 (observe that \(q\not=n\) in this case), we obtain that

which implies that right>2left−1 and, hence, right≥2left since right and left are integers. Together with the inequality between right and left derived above we obtain that left=right=0 which contradicts our assumptions. Hence, one of the players q−left and q+right has an incentive to change her strategy. □

We are now ready to prove our lower bound for broadcast games.

Theorem 9

For any δ>0, there exists a broadcast game with price of stability at least 20/11−δ.

Proof

Consider the broadcast game on the graph B n in which C is defined as follows.

  • \(z_{n} = z_{n-1} = \frac{9}{5}\),

  • \(z_{i} = \frac{8}{5} (\frac{8}{9} )^{n-2-i}\), for i=1,…,n−2,

  • \(x_{n} = \frac{9}{10}+\epsilon\),

  • \(x_{i} = (\frac{8}{9} )^{n-1-i}+\epsilon\), for i=2,…,n−1,

where ϵ>0 is arbitrarily small.

It is easy to check that C satisfies the conditions of Lemma 8. Hence, the assignment defined by tree τ is the unique Nash equilibrium of the broadcast game on B n . Its cost is

In order to upper-bound the optimal cost, it suffices to consider the tree that uses edge (s,t 1) and edges (t i ,t i+1) for i=1,…,n−1. Its cost is at most

Now, given any δ>0, it is clear that we can set n sufficiently large and ϵ sufficiently small so that the ratio between the cost of the unique Nash equilibrium and the optimal cost is at least 20/11−δ. □

We remark that the graph B n has the same structure with the lower bound construction of [7] albeit with a different definition of the edge costs that yields the improved lower bound on the price of stability.

5 Conclusions and Open Problems

Of course, our work leaves open the major question of whether the price of stability in undirected design games grows with n or not. Following [6], it is tempting to conjecture that the price of stability is constant at least for broadcast and multicast games. Note that the game used in the proof of our lower bound for multi-soure network design games has a special structure. It is defined in a connected undirected graph in such a way that there is a distinct player associated with each edge that aims to connect the endpoints of the edge. We believe that studying this specific class of undirected network design games is of interest as well.