The remote set problem on lattices

Abstract

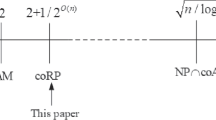
We initiate studying the Remote Set Problem (${\mathsf{RSP}}$) on lattices, which given a lattice asks to find a set of points containing a point which is far from the lattice. We show a polynomial-time deterministic algorithm that on rank n lattice ${\mathcal{L}}$ outputs a set of points, at least one of which is ${\sqrt{\log n / n} \cdot \rho(\mathcal{L})}$ -far from ${\mathcal{L}}$ , where ${\rho(\mathcal{L})}$ stands for the covering radius of ${\mathcal{L}}$ (i.e., the maximum possible distance of a point in space from ${\mathcal{L}}$). As an application, we show that the covering radius problem with approximation factor ${\sqrt{n / \log n}}$ lies in the complexity class ${\mathsf{NP}}$ , improving a result of Guruswami et al. (Comput Complex 14(2): 90–121, 2005) by a factor of ${\sqrt{\log n}}$ .

Our results apply to any ${\ell_p}$ norm for ${2 \leq p \leq \infty}$ with the same approximation factors (except a loss of ${\sqrt{\log \log n}}$ for ${p = \infty}$). In addition, we show that the output of our algorithm for ${\mathsf{RSP}}$ contains a point whose ${\ell_2}$ distance from ${\mathcal{L}}$ is at least ${(\log n/n)^{1/p} \cdot \rho^{(p)}(\mathcal{L})}$ , where ${\rho^{(p)}(\mathcal{L})}$ is the covering radius of ${\mathcal{L}}$ measured with respect to the ${\ell_p}$ norm. The proof technique involves a theorem on balancing vectors due to Banaszczyk (Random Struct Algorithms 12(4):351–360, 1998) and the “six standard deviations” theorem of Spencer (Trans Am Math Soc 289(2):679–706, 1985).