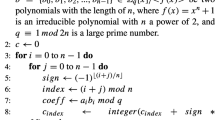A Masked Ring-LWE Implementation

Abstract

Lattice-based cryptography has been proposed as a postquantum public-key cryptosystem. In this paper, we present a masked ring-LWE decryption implementation resistant to first-order side-channel attacks. Our solution has the peculiarity that the entire computation is performed in the masked domain. This is achieved thanks to a new, bespoke masked decoder implementation. The output of the ring-LWE decryption are Boolean shares suitable for derivation of a symmetric key. We have implemented a hardware architecture of the masked ring-LWE processor on a Virtex-II FPGA, and have performed side channel analysis to confirm the soundness of our approach. The area of the protected architecture is around 2000 LUTs, a $20\,\%$ increase with respect to the unprotected architecture. The protected implementation takes 7478 cycles to compute, which is only a factor $\times 2.6$ larger than the unprotected implementation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Once the quantum computer is built, Shor’s algorithm will make most current cryptographic algorithms obsolete. In particular, public-key cryptosystems that rely on number-theoretic hardness assumptions such as integer factorization (RSA) or discrete logarithms, either in $\mathbb {Z}_p^*$ (Diffie-Hellman) or in elliptic curves over finite fields, will be insecure. On the bright side, there is an entire branch of postquantum cryptography that is believed to resist mathematical attacks running on quantum computers.

There are three main branches of postquantum cryptosystems: based on codes, on multivariate quadratic equations or on lattices [1]. Lattice-based cryptographic constructions, founded on the learning with errors (LWE) problem [21] and its ring variant known as ring-LWE problem [15], have become a versatile tool for designing asymmetric encryption schemes [15], digital signatures [8] and homomorphic encryption schemes [3, 9]. Several hardware and software implementations of such schemes have appeared in the literature. So far, the reported implementations have focused mainly on efficient implementation strategies, and very little research work has appeared in the area of side channel security of the lattice-based schemes.

It comes as no surprise that implementations of postquantum algorithms are vulnerable to side-channel attacks. Side-channel attacks, as introduced by Kocher [13], exploit timing, power consumption or the electromagnetic emanation from a device executing a cryptographic implementation to extract secrets, such as cryptographic keys. A particularly powerful side-channel technique is Differential Power Analysis (DPA), introduced by Kocher et al. [14]. In a typical DPA attack, the adversary measures the instantaneous power consumption of a device, places hypotheses on subkeys and applies statistical tests to confirm or reject the hypotheses. DPA attacks can be surprisingly easy to mount even with low-end equipment, and hence it is important to protect against them.

There are plenty of countermeasures against DPA. Most notably, masking [6, 12] is both a provably sound and popular in industry. Masking effectively randomizes the computation of the cryptographic algorithm by splitting each intermediate into several shares, in such a way that each share is independent from any secret. This property is preserved through the entire computation. Thus, observing any single intermediate (for example, by a side-channel, be it known or unknown) reveals nothing about the secret. However, there are not many masking schemes specifically designed for postquantum cryptography. In [4] Brenner et al. present a masked FPGA implementation of the post-quantum pseudo-random function SPRING.

In the rest of the paper, we focus on protecting the ring-LWE decryption operation against side-channel attacks with masking. The decryption algorithm is considerably exposed to DPA attacks since it repeatedly uses long-term private keys. In contrast, the encryption or key-generation procedures use ephemeral secrets only [24].

Our contribution. In this paper we present a very compact masked implementation of the ring-LWE decryption function. The masking countermeasure adds very limited overhead compared to other previous approaches, thanks to a bespoke probabilistic masked decoder designed specifically for our implementation. We implemented the design on a Virtex-II FPGA and tested the side-channel security with practical experiments that demonstrate the validity of our approach.

Organization. The paper is structured as follows: we provide a brief mathematical background of the ring-LWE encryption scheme in Sect. 2 and describe a high-level overview of the proposed masked ring-LWE decryption in Sect. 3. In the next section we construct the masked decoder and in Sect. 5 we show the experimental results. We analyze the error rates of the decryption operation in Sect. 6 and apply error correcting codes. We dedicate Sect. 7 for the side channel evaluation.

2 Preliminaries

Notation. The Latin letters r, $c_i$ indicate polynomials. When we want to explicitly access a coefficient of the polynomial we write r[i]. Multiplication of polynomials is written as $r*c_1$. Coefficient-wise multiplication is denoted as $r\cdot c_1$. The letter m denotes a string of bits, and q is an integer. Letters with prime $x'$ or double prime $x''$ represent shares of variable x. Depending on the context, these shares are split either arithmetically $x= x' + x'' \pmod q$ or Boolean $x=x' + x'' \pmod 2$. A polynomial r is shared into $(r',r'')$ by additively sharing each of its coefficients r[i] such that $r = r' + r''$.

Ring-LWE. For completeness, we give in this section a description of the three major algorithms of the ring-LWE public-key cryptosystem [15]: key-generation, encryption and decryption.

The ring-LWE encryption scheme works with polynomials in a ring $R_q=\mathbb {Z}_q[\mathbf {x}]/(f(x))$, where f(x) is an irreducible polynomial of degree n. During the key generation, encryption and decryption operations, polynomial arithmetic such as polynomial addition, subtraction and multiplication are performed. In addition, the key-generation and encryption operations require sampling of error polynomials from an error distribution (typically a discrete Gaussian.)

The ring-LWE encryption scheme is described in this way:

• In the key generation phase, two error polynomials $r_1$ and $r_2$ are sampled from the discrete Gaussian distribution. The secret key is the polynomial $r_2$ and the public key is the polynomial $p = r_1 - g * r_2$. After key generation, there is no use of the polynomial $r_1$. The polynomial g is globally known.

• In the encryption operation of a binary message vector m of length n, the message is first lifted to a ring element $\bar{m} \in R_q$ by multiplying the message bits by q / 2. The ciphertext is computed as a pair of polynomials $(c_1,c_2)$ where $c_1=g * e_1 + e_2$ and $c_2=p* e_1 + e_3 + \bar{m} \in R_q$. The encryption operation requires generation of three error polynomials $e_1$, $e_2$ and $e_3$.

• The decryption operation uses the private key $r_2$ to compute the message as $m = {\text {th}}(c_1 * r_2 + c_2)$. The decoding function ${\text {th}}$ is a simple threshold decoder that is applied coefficient-wise and is defined as

  $$\begin{aligned} {\text {th}}(x) = \left\{ \begin{array}{lrl} 0 &{} \ \text {if}\ x \in &{}(0,q/4) \cup (3q/4,q)\\ 1 &{} \ \text {if}\ x \in &{}(q/4,3q/4) \end{array} \right. \end{aligned}$$

  (1)

Efficiency improvements. To achieve an efficient implementation of the encryption scheme, the irreducible polynomial f(x) is taken as $x^n+1$ where n is a power of two, and the modulus q is chosen as a prime number satisfying $q \equiv 1 \mod 2n$ [18, 25]. In this setting, polynomial multiplications can be efficiently performed in $O(n\log n)$ time using the Number Theoretic Transform (NTT).

Following [25], we keep the ciphertext polynomials $c_1$ and $c_2$ in the NTT domain to reduce the computation cost of the decryption operation. The decryption operation thus computes the decrypted message as

$$\begin{aligned} m = {\text {th}}\big ({\text {INTT}}(\tilde{c}_1 \cdot \tilde{r}_2 +\tilde{c}_2)\big ). \end{aligned}$$

(2)

Here the symbol $\tilde{r}$ represents the NTT of a polynomial r, and ${\text {INTT}}(\cdot )$ represents the inverse NTT operation. The multiplication of $\tilde{c}_1 \cdot \tilde{r}_2$ is thus performed coefficient-wise (as well as the addition $\tilde{c}_1 \cdot \tilde{r}_2 + \tilde{c}_2$.) For convenience, we drop the tildes in the rest of the paper and work with $c_1$, $c_2$ and $r_2$ in the NTT domain. We furthermore refer to $\tilde{r}_2$ simply as r. (We recall that the INTT is a linear transformation applied to the n coefficients of $a=r \cdot c_1 + c_2$.) The decoding function ${\text {th}}$ applies a threshold function to each coefficient of a as defined in Eq. 1 to output n recovered message bits.

3 High-Level Overview

In this section, we give a high-level view of the masked ring-LWE implementation. The most natural way to split the computation of the decryption as Eq. 2 is to split the secret polynomial r additively into two shares $r'$ and $r''$ such that $r[i]=r'[i] + r''[i] \pmod q$ for all i. The n coefficients of $r'$ are chosen uniformly at random in $\mathbb {Z}_q$ in each execution of the decryption.

Fig. 1.

General data flow of the masked ring-LWE decryption. $r'$ and $r''$ are the arithmetic shares of the private key r; $c_1$ and $c_2$ are the input unmasked ciphertext; $m'$ and $m''$ are the Boolean shares of the recovered plaintext.

The bulk of the computation from Eq. 2 is amenable to this splitting, since by linearity of the multiplication and INTT operation, we have that ${\text {INTT}}(r\cdot c_2 + c_1) = {\text {INTT}}(r' \cdot c_2 + c_1) + {\text {INTT}}(r'' \cdot c_2)$. Thus, we can split almost the entire computation from Eq. 2 into two branches, as drawn in Fig. 1. The first branch computes on $r'$ to determine the polynomial

$$\begin{aligned} a'= {\text {INTT}}(r' \cdot c_2 + c_1) \end{aligned}$$

(3)

and the second branch operates on $r''$ to determine

$$\begin{aligned} a'' = {\text {INTT}}(r''\cdot c_2). \end{aligned}$$

(4)

The advantage of such a high-level masking is that the operations of Eqs. 3 and 4 can be performed on an arithmetic processor without any particular protection against DPA. (This is because any intermediate appearing in either branch is independent of the secret r. This situation is very similar to, for example, base point blinding in elliptic curve scalar multiplication.) We can reuse an existing ring-LWE processor for these operations, and leverage the numerous optimizations carried out for this block [18, 25].

The final threshold ${\text {th}}(\cdot )$ operation of Eq. 2 is obviously non-linear in the base field $\mathbb {F}_q$, and hence cannot be independently applied to each branch (Eqs. 3 and 4). There are generic approaches to mask arbitrary functions. For instance, in [4] an approach based on masked tables was used. However, these generic approaches are usually quite expensive in terms of area or randomness. In the following Sect. 4, we pursue another direction. We design a bespoke masked decoder that results in a very compact implementation.

4 Masked Decoder

In this section we describe a very compact, probabilistic masked decoder. In the sequel, a denotes a single coefficient and $(a',a'')$ its shares such that $a'+a''=a \pmod q$. The decoder computes the function ${\text {th}}(a)$ from the shares $(a',a'')$. We also drop the symbol $\pmod q$ when obvious.

First crack. The key idea of the efficient masked decoder is that we do not need to know the exact values of the shares $a'$ and $a''$ of a coefficient a in order to compute ${\text {th}}(a)$. For example, if $0<a'<q/4$ and $q/4<a''<q/2$ then $a = a'+a''$ is bounded by $q/4<a<3q/4$, and thus ${\text {th}}(a)=1$. That is, we learnt ${\text {th}}(a)$ from only a few most significant bits from $a'$ and $a''$. We can use this idea to substantially simplify the complexity of the masked ${\text {th}}$ function.

Fig. 2.

Idea for the masked decoder. Elements in $\mathbb {Z}_q$ are shown in a circle. Adding two elements translates into adding their respective angles. Left: case $0<a'<q/4$, $q/4 < a'' < q/2$, and therefore ${\text {th}}(a)=1$. Center and right: case $0<a'<q/4$, $0<a''<q/4$, which does not allow to infer ${\text {th}}(a)$.

4.1 Rules

Figure 2, left, illustrates the situation from the last paragraph. In this case, $0<a'<q/4$ and $q/4 < a'' < q/2$ so obviously a can range only from q / 4 to 3q / 4, and hence ${\text {th}}(a)=1$. Analogously to this rule, we can formulate 3 other rules:

• If $q/2<a'<3q/4$ and $3q/4<a''<q$ then $q/4<a<3q/4$ and thus ${\text {th}}(a) =1$.

• If $q/4<a'<q/2$ and $q/2<a''<3q/4$ then a belongs to $(0,q/4)\cup (3q/4,q)$ and thus ${\text {th}}(a) = 0$ (quadrants I and IV, left half of the circle).

• If $3q/4<a'<q$ and $0<a''<q/4$ then a belongs to $(0,q/4)\cup (3q/4,q)$ and thus ${\text {th}}(a) = 0$.

There are 4 other rules that result from interchanging $a'$ with $a''$ in the above expressions. (This follows straight from the symmetry of the additive splitting.) Essentially, with the only information of the quadrant of each share $a'$ and $a''$ we can, in half of the cases, deduce the output of ${\text {th}}(a)$. (For the explanation simplicity, we obviated what happens in the boundaries of the quadrant intervals. Similar conclusions hold when including them.)

What if no rule is hit? In roughly half of the cases, we can apply one of the 8 rules previously described to deduce the value of ${\text {th}}(a)$. However, in the other half of the cases, none of the rules applies. A representative case of this event is shown in Fig. 2, center and right. In both cases, $0<a'<q/4$ and $0<a''<q/4$. This situation is not covered by any of the 8 rules previously described. We see that in the center sub figure ${\text {th}}(a)=0$ while in the right sub figure ${\text {th}}(a)=1$, so in this case the quadrants of each share $a'$ and $a''$ do not allow us to infer ${\text {th}}(a)$.

The solution in this case is to refresh the splitting $(a',a'')$, that is, update $a'\leftarrow a'+\varDelta _1$ and $a'' \leftarrow a'' - \varDelta _1$ for certain $\varDelta _1$. (This refreshing naturally preserves the unshared value $a = a' + a''$.) After the refreshing, the 8 rules can be checked again. If still no rule applies, the process is repeated with a different refreshing value $\varDelta _i$. Note that in each iteration of the step, roughly half of the possible values of $(a', a'') \in \mathbb {Z}_q \times \mathbb {Z}_q$ are successfully decoded, and thus the amount of pairs $(a',a'')$ that do not get decoded shrinks exponentially with the number of iterations. In our implementation, $N=16$ iterations produces a satisfactory result. This will be studied in detail in Sect. 6.1.

Optimal cooked values for $\varDelta _i$. One can determine a sequence of $\varDelta _i$ values that maximizes the number of pairs successfully decoded after N iterations. We performed a first-order search for such a sequence of $\varDelta _i$ values. Each $\varDelta _i$ maximizes the number of successfully decoded pairs after $i-1$ iterations. See the extended version of this paper¹ for exemplary values of $\varDelta _i$.

Fig. 3.

The masked decoder.

Architecture. The hardware architecture for the masked decoder follows from the previous working principle description. Our implementation is shown in Fig. 3. From left to right, we see the first refreshing step by the constants $\varDelta _i$. The constants $\varDelta _i$ vary from iteration to iteration. After the refreshing step, the quadrant function is applied to each share $a',a''$. This quadrant function outputs x if a belongs to the x-th quadrant, and thus the output consists of 2 bits. These blocks are essentially 13-bit comparators, and thus relatively inexpensive in logic.² The subsequent rule checking on $(q',q'')$ is performed by a masked table lookup that is described in the following section. The whole process is repeated $N=16$ iterations, and this number of iterations stays fixed even if the decoding is successful after the few first iterations.

4.2 Masked Table Lookup

The final step in the masked decoder is a masked table lookup. This table implements the rules described in Sect. 4.1, and essentially maps the output of each quadrant $q'_i$ and $q''_i$ (2 bits each) after the i-the iteration ($i\in [1,N]$) to a (Boolean) masked output bit value $(m'_i,m''_i)$. In our specific implementation, we have other inputs: the result of the decoding from the previous iteration $(m'_{i-1}, m''_{i-1})$ and an extra randomness bit r (fresh at each of the N iterations for each of the n coefficients).

This is a well-studied problem that arises in other situations (for instance, when masking the sbox lookup in a typical block cipher) and there are plenty of approaches here to implement such masked table lookup. We opted for the approach of masked tables as in [26]. We set $m'_i \leftarrow r$ and we compute $m''_i \leftarrow f(r,q'_i,q''_i,m'_{i-1},m''_{i-1})$. The function f essentially bypasses the previous decoded value when no rule applies to $q'_i,q''_i$ by setting the output $m''_i$ to $r + m'_{i-1} + m''_{i-1}$ (refreshing the content of the output registers). If a rule applies to $q'_i, q''_i$, it sets the output $m''_i$ accordingly. By doing this, we can register always the output of this table and no control logic to enable such output register is needed (it is implicitly integrated into this masked table.) This is the reason why the table sees also the previous decoded value $m'_{i-1}$ and $m''_{i-1}$.

The usual precautions are applied when implementing f. For our target FPGA platform, we carefully split the 7-bit input to 1-bit output function f into a balanced tree of 4-bit input LUTs, in such a way that any intermediate input or output of LUTs does not leak in the first order. Note that here we are assuming that each LUT is an atomic operation. If stronger security guarantees are needed, other approaches to implement such function f should be followed. When implemented in an ASIC, it may be preferable to store this masked table in ROM (since the contents of the table are immutable and the size is small.)

The output of this table is (Boolean) masked, and thus no unmasked value lives within the implementation. This is suited for consumption of a masked AES module (say) after some preprocessing as will be detailed later. We stress that we use masked tables on the output of the quadrants. This is the key for our reduced area requirements, as will be explained in the next Sect. 5.

5 Implementation Results

We implemented the fully masked ring-LWE decryption system with the parameter set $(n,q,s)=(256,7681,11.32)$ first introduced in [11], corresponding to a medium-term security level. The target platform is a Xilinx Virtex-II xc2vp7 FPGA. The HDL files were synthesized within Xilinx ISE v8.2 with optimization settings set to balanced and KEEP HIERARCHY flag when appropriate to prevent optimization of security-critical components. We base our arithmetic processor on the design from [25].

5.1 Area

In our case, a single arithmetic coprocessor performs serially the computations of Eq. 3 and then that of Eq. 4. This incurs in a very slight area overhead (only the control microcode is slightly modified, plus the masked decoder), at the obvious cost of an increased execution time. In comparison to the unprotected version, our protected decryption scheme consumes more memory as now we store two shares $r'$ and $r''$ of the secret polynomial r, and the two output polynomials $a'$ and $a''$ from the two INTT operations.

In Table 1, we can see that the proposed masking of the ring-LWE architecture incurs an additional area overhead of only 301 LUTs and 129 FFs in comparison to the unprotected version. This additional area cost is mostly due to a pair of masked decoders. Due to its low area overhead, we chose to keep two masked decoders in parallel, decoding two coefficients simultaneously. (This nicely fits with the memory organization of the arithmetic coprocessor, since it fits two 13-bit coefficients in each memory word.) Thus, we use two addition and subtraction circuits for the refreshing with $\varDelta _i$ (accounting for 160 LUTs) and two masked tables (90 LUTs in total.)

We note that we could straightforward reduce the additional area cost by reusing the 13-bit addition and subtraction circuits present in the arithmetic coprocessor. Since during a decoding operation, the arithmetic coprocessor remains idle, reusing of the addition and subtraction circuits do not cause any increase in the cycle count. For simplicity, we did not implement this approach.

Table 1. Performance and Comparison on Xilinx Virtex-II xc2vp7 FPGA. Note that these results are not directly comparable with [25], since the latter were obtained from a more advanced Virtex-6 FPGA, which has 6-bit input LUTs and superior routing mechanisms in comparison to our target FPGA.

5.2 Cycle Count

The cycle count for our approach is decomposed in the computation of Eqs. 3 and 4 and the masked decoder. Equation 3 takes 2840 cycles (one unprotected ring-LWE decryption), Eq. 4 takes 2590 cycles, slightly less than Eq. 3 since there is no addition present in the second branch.

The two-way parallel masked decoder takes $\frac{1}{2} \times n \times N+\epsilon$ cycles to decode all the coefficients into message bits. In our case with $n=256$, $N=16$ the masked decoder takes 2048 cycles. Thus in total, a masked decryption operation requires 7478 cycles. The arithmetic coprocessor and the masked decoder run in constant time and constant flow.

5.3 Comparison with an Elliptic-Curve Cryptosystem

We compare our protected decryption scheme with the unprotected high-speed elliptic curve scalar multiplier architecture proposed by Rebeiro et al. in [20]. The architecture for the field $\text {GF}(2^{233})$ consumes $23\ 147$ LUTs and computes an unprotected scalar multiplication in 12.5 $\mu$s on a more advanced Virtex-4 FPGA. Thus the scalar multiplier has an area $\times$ time product of approximately $289\ 337$. Our protected ring-LWE decryption (for a similar security) achieves an area $\times$ time product of approximately $151\ 452$ on a Virtex-2 FPGA; thus achieving at least 1.9 times better figure of merit.

5.4 Trade-offs

The previous figures are subject to trade-offs. If smaller latency is desired instead of a compact implementation, two coprocessors can perform the two computations of Eqs. 3 and 4 in parallel. Trade-offs also apply to the masked decoder, and the parallelization could be extended easily to reduce latency in this stage. Since the BRAMs present in the Xilinx FPGAs support reading of multiple consecutive words, we could keep more pairs of masked decoders in parallel and reduce the number of cycles. Another alternative is to keep the masked decoder in pipeline with the polynomial arithmetic block. Such type of setting is suitable for systems where many decryption operations are performed in a chain. While the masked decoder works on the coefficients of a previous computation, the polynomial arithmetic unit processes new ciphertexts. Since the masked decoder is faster than the polynomial arithmetic unit, the cycle count of the masked decoder is not an overhead in such type of setting. But of course, in this situation we could not reuse the arithmetic circuitry of the arithmetic coprocessor for the refreshing operation of the masked decoder.

5.5 Maximum Frequency

We note that the arithmetic coprocessor is a very optimized unit with a complex pipeline organization. We thus insert two pipeline stages in the masked decoder to match the maximum frequency of the whole system to that of the arithmetic coprocessor. In this way, the design can run up to almost 100  MHz. The critical path is inside the arithmetic multiplier.

6 Discussion

6.1 Error Rates

Cryptosystems based on ring-LWE are inherently probabilistic. This means that there is a non-zero probability that the recovered plaintext after ring-LWE decryption is not exactly the plaintext before encryption. In our case, due to the probabilistic nature of our masked decoder approach, there is a second source of noise. Since the number of iterations of the masked decoder is finite, there are some pair values $(a',a'')$ that will not get decoded within the fixed finite number of iterations. In this section, we first explain the error rate of the probabilistic decoding in isolation, and then we switch to the global system error rate and point out strategies to mitigate it.

Errors due to the probabilistic decoding. In this section, we assume that the plaintext bit is 1 and the unmasked input a to the masked decoder is in (q / 4, 3q / 4). The additional error due to the probabilistic masked decoder is the probability $p_e$ that $(a',a'')$ does not get successfully decoded. Let us write $p_s = 1-p_e$.

This probability $p_s$ is influenced by two distributions. We have that

$$\begin{aligned} p_s = \sum \Pr [\text {successful decode}|a] \cdot \Pr [a] \end{aligned}$$

(5)

where the sum is taken over $a\in (q/4,3q/4)$. On the one hand, $\Pr [\text {successful decode}|a]$ is the probability that the decoder successfully decodes a. On the other, $\Pr [a]$ is the probability with which a takes various values in (q / 4, 3q / 4).

Fig. 4.

Left: empirical success distribution for the masked decoder. Right: Distribution of a when plaintext is 1.

The distribution of the decoder success probability $\Pr [\text {successful decode}|a]$ as a function of the unshared input value a to the decoder can be easily computed by averaging over all possible pairs $(a',a'')$ such that $a'+a''=a$. Since for any given value of a, its shares $a'$ or $a''$ are (individually) equiprobable, we compute $\Pr [\text {successful decode}|a]$ as $\Pr [\text {successful decode}|a] = \frac{1}{q}\sum _{a'+a''=a} \Pr [\text {successful decode of }(a',a'')]$.

The distribution $\Pr [\text {successful decode}|a]$ is shown in Fig. 4, left. We see that the decoder performs best when $a\approx q{/}2$, in which case all possible inputs get decoded correctly. Only when the input value a approaches q / 4 or 3q / 4, the performance degrades. When using a larger number of iterations $N=16$ this effect is less pronounced when compared to $N=2$ iterations, as Fig. 4 shows.

On the other hand, it is easy to see that not all unshared inputs a to the decoder are equally likely. By the construction of the ring-LWE decryption function, the unshared input to the decoder a is either centered around q / 2 (resp. 0) when the message bit is 1 (resp. 0). This distribution $\Pr [a]$ is plotted in Fig. 4, right.

These two observations combined produce a nice interaction between the prior distribution $\Pr [a]$ of a (given by the ring-LWE decryption) and the success distribution of the masked decoder $\Pr [\text {successful decode}|a]$ as in Eq. 5. Namely, values of a that are difficult to decode (those with low $\Pr [\text {successful decode}|a]$) are quite unlikely to appear as input to the masked decoder (their $\Pr [a]$ is also low). This positive interaction keeps the global error rate of the system quite low. This is precisely quantified in the next paragraph.

Fig. 5.

Global error rates with the probabilistic decoder.

Fig. 6.

Evolution of the ratio $p_g / p_\text {baseline}$ as the number of iterations N grows.

Global error rate and number of iterations. We performed simulations to estimate the global error rate and determine the required number of iterations N in our design. Over $10^6$ bits, the average error per bit using a deterministic decoder was $p_\text {baseline}=3.634375 \times 10^{-5}$. This is a baseline error intrinsic to the ring-LWE construction. When we plug in the probabilistic decoder, the global, end-to-end, error rate per bit $p_g$ increases. (We have $p_g = p_\text {baseline}+p_e$.) In Fig. 5, we can find the global error rate for different values of the number of iterations N of the decoding. At $N=3$, for instance, the error rate is $p_g= 1.7844 \times 10 ^{-3}$, which is $\approx 49$ times larger than $p_\text {baseline}$. As already hinted, the error rate quickly decreases with N (roughly exponentially, as can be see in Fig. 6). In our design, we set $N=16$ (we iterate 16 times per coefficient) as a balanced tradeoff between cycle count and error rate. The impact of the masked probabilistic decoder on the global error rate is quite low, adding less than $20\,\%$ to the intrinsic error rate when compared to a deterministic decoder, as it can be see in Fig. 5.

6.2 Comparison with Other Decoding Strategies

We are only aware of a similar masked decoder, the one presented in [4]. There the authors resort to a generic masking method, namely masked tables, to perform the decoding. Translating the ideas of [4] in our context, we would need two tables of $2^{13}$ bits (one of them random). For a smaller group $\mathbb {Z}_d$ with $d=257$ the authors report an utilization of 1331 slices on a Virtex 6 FPGA. While the results in slices are not directly comparable with ours, we point out that the size of the masked table following the approach of [4] grows linearly in the group size q, while for our solution the size of the masked table stays constant (independent of q), and the quadrant blocks grow only logarithmically in q. The cycle count, however, is larger in our solution. The critical observation of our masked decoder is that we can compress the input coefficient shares $a'$ and $a''$ to a mere two bit per share (the output of each quadrant) and then perform the decoding based on the information of the two quadrants (4 bits.)

6.3 Post-Processing

Albeit the computation from Eq. (2) is commonly referred as the “ring-LWE decryption”, the decryption process should include a post-processing on the recovered message m. This post-processing consists of error correction and padding verification.

Linear codes with masking. One approach to deal with the probabilistic nature of the ring-LWE decryption system is to use forward error correcting codes (FEC). The message prior to encryption is encoded using a FEC and the resulting composite is ring-LWE encrypted. The output of the ring-LWE decryption should be corrected for errors, preferably in the masked domain. For syndrome decoding of linear codes, this can easily be done by masking the syndrome table.

Padding schemes. As presented, the ring-LWE system is malleable. CCA security can be achieved with a padding mechanism. The Fujisaki-Okamoto [10] padding scheme is known to work with ring-LWE [17]. This padding scheme makes use of standard symmetric cryptographic constructions whose masked implementations are well studied. We point out that key-encapsulation mechanisms may result in a more compact and simpler implementation.

6.4 Extension to Higher-Order Security

We point out that the approach laid out in Sect. 3 scales quite well with the security order. To achieve security at level $d+1$, one would need to split the computation of Eq. 2 into d branches analogously to Eq. 3. The masked decoder can follow the same principles with the appropriate modifications. The complexity of this decoder obviously grows. Generic approaches to perform this computation have been discussed in [2, 7, 22].

7 Evaluation

For the purposes of a side-channel evaluation, we implemented the full design on a SASEBO G board. The design was clocked at 18.75 MHz and the power consumption was sampled at 500 MS/s. This platform is very low noise.

We provide a very advantageous setting for the adversary: we assume that the evaluator knows the details about the implementation (for example, pipeline stages). In addition, we assume that while guessing a subkey, the adversary knows the rest of the key. These assumptions allow to comfortably place predictions on intermediates arbitrarily deep into the computation. While this may represent a very powerful attacker and somewhat unrealistic, the algebraic structure of such cryptosystem may help the attacker to predict deep intermediates with relatively low effort. We refer the reader to the extended version of this paper for an attack on half-masked ring-LWE decryption that uses these ideas. This stresses the necessity of masking the decoding function entirely.

The evaluation methodology to test if the masking is sound is as follows. We first proceed with first-order key-recovery attacks when the randomness source (PRNG) is switched off. We demonstrate that in that situation the attacks are successful, indicating that the setup and procedure is sound. Then we switch on the PRNG and repeat the attacks. If the masking is sound, the first-order attacks shall not succeed. In addition, we perform second-order attacks to confirm that the previous first-order analyses were carried out with enough traces.

We test 4 different points which covers all the relevant parts of the computation. The targets are the first 13-bit coefficient of $r'\cdot c_1 + c_2$, the first 13-bit coefficient of $r''\cdot c_1$, the first input coefficient to the shared decoder and the first output bit. We modeled the power consumption of a register as the Hamming distance between two consecutive values held in the register, and used Pearson’s correlation coefficient to compare predictions with measurements [5].

Fig. 7.

PRNG off. On top, black, one power consumption trace. The different computational stages can be distinguished: first branch, second branch and decoding. Next, in blue, the correlation trace for the value $r'[0]\cdot c_1[0] + c_2[0]$. The correlation achieves a maximum value of $\rho = 0.25$. Below, in red, correlation for $r''\cdot c_1$ (max $\rho \approx 0.3$); in green: correlation for the input of the masked decoder $a'[0]$. At the bottom: correlation with one message bit $m'[0]$ (Color figure online).

7.1 PRNG Off

We first begin the experiments when the PRNG is off. That is, the sharing of r into $r'$ and $r''$ on each execution is deterministic. This would not happen in practice, as an active PRNG would randomize the representation of r in each execution. In our setting, this would mean that the masking is switched off.

Fig. 8.

PRNG off. Evolution of the correlation coefficient as the number of traces increases for the intermediates $r'[0]\cdot c_1[0] + c_2[0]$ (left) and $r''[0]\cdot c_1[0]$ (right). Correct subkey guess in red, all other guesses in green. A 99.99 % confidence interval for $\rho = 0$ is plotted in black discontinuous line. We can see that starting from hundred measurements the attacks are successful (Color figure online).

In Fig. 7 we draw the result of correlating against the 4 intermediates with $10\ 000$ traces. On top, we draw a mean trace for orientation. The correlation values are, from top to bottom, 0.25, 0.3, 0.27 and 0.21, respectively. This means that the attacks are successful, and confirms the soundness of our setting. In Fig. 8 we can see the evolution of the correlation coefficient as the number of traces increases for the first two intermediates. We can see that starting from hundred traces the attack is successful. Similar behavior was observed for other intermediates.

Fig. 9.

Analogous to Fig. 8, but with PRNG on. The correct subkey is no longer identifiable. This is expected and means that the masking is effective.

7.2 PRNG On

In Fig. 9 we draw the result of the previous analysis when the masks are switched on. This corresponds to the situation that an adversary would face in reality. We can see that the correct key guess is no longer distinguishable, even when using $10\ 000$ traces. We repeated the same experiments for other intermediates and other intermediate positions with identical results.

7.3 Second-Order Attacks

To confirm that we used enough traces in our previous analyses, we perform here second-order attacks on the masked implementation with the PRNG on. We will focus on the masked decoder. In Fig. 10 we draw on top a mean curve in the region of $7\ 400$ to $7\ 700$ cycles, corresponding to the end of the masked decoding. We target one output bit of the decoding: m[254].

Fig. 10.

Correlation traces for intermediates within the shared decoder. On top, a power measurement trace showing the last 15 decodings. Below, correlation traces. The first two (masks and masked values) assume that the adversary knows the masks. The third one, in light blue, is a first-order attack without knowing the attack, and is unsuccessful. In contrast, the second-order attack against the same intermediate is successful, as the traces in magenta and yellow show (Color figure online).

In Fig. 10 we first begin by correlating against masks and masked values. This is a test scenario, since for this attack we need to know the masks, something that would not happen in a real deployment. Correlation with masks or masked value yield high correlation as expected ($\rho = 0.32$ and $\rho = 0.34$, respectively). In contrast, when correlating against the unshared value (in light blue), the correlation coefficient does not traverse the confidence interval for $\rho = 0$. This indicates that the masking is effective. We can repeat the same attack against centered and squared traces [6, 19]. This is effectively a second-order attack, and is expected to work. It is shown in magenta in Fig. 10, and we can see that the attack succeeds. Using the centered absolute value to pre-process traces also works as expected, as shown in yellow.

Fig. 11.

Left: correlation as the number of traces increases for the first-order attack (PRNG on), around clock cycle 7560. Right: correlation for the second-order attack with masks on. The attack begins to be successful with $2\ 000$ measurements.

Fig. 12.

Crosscorrelation trace. The x and y axes represent time, flowing from the upper left hand side corner to the lower right. The entire figure spans 7500 cycles (as Fig. 7). It is possible to distinguish the two branch computations (including its components) and the decoding. Colors enhanced to improve contrast (Color figure online).

In Fig. 11 we can see the evolution as a function of the number of traces. We can see that starting from ${\approx }2000$ measurements this second-order attack is successful. This confirms that the first-order attacks of Sect. 7.2 were carried out with enough traces, since a second-order attack is already successful starting from ${\approx }2000$ measurements.

We remark that the relatively low number of traces required for the second-order attack is due to the very friendly scenario for the evaluator. The platform is low noise and no other countermeasure except than masking was implemented. In practice, masking needs a source of noise to be effective, and consequently the higher-order attacks would be harder to mount, requiring more traces [6] and more computation [23].

7.4 Horizontal DPA Attacks

During the decoder operation, the input coefficients are refreshed $N-1=15$ times with publicly known offsets $\varDelta _i$. The device thus handles consecutively the values $a'$, $a'+\varDelta _1$, ..., $a'+\varDelta _1 + \ldots + \varDelta _{15}$. This may enable a horizontal DPA attack [16] during the operation: the adversary may collect a single trace, split it into 16 chunks and then perform a DPA on these 16 chunks to recover the mask $a'$. Once the masks from all traces are discovered, a first-order, vertical DPA applies (Fig. 12).

There are two factors that mitigate this threat. First, we note the adversary is given a very limited number of traces to recover each mask (namely, $N=16$). Secondly, this attack can be easily prevented by shuffling the public coefficients $\varDelta _i$. This randomizes the order of execution of each refreshing with $\varDelta _i$, and thus the exposure to horizontal DPA attacks is minimized.

8 Conclusion

In this paper we described a practical side-channel protected implementation of the lattice-based ring-LWE asymmetric decryption. Our solution is based on the sound principles of masking and incurs in a manageable overhead (in cycles and area). A key component of our solution is a bespoke masked decoder. Our implementation performs the entire ring-LWE decryption computation in the masked domain.