Keywords

1 Introduction

A grid consists of several tiles/pixels. A step is moving from one pixel to another, neighbor one. Each step has a positive length depending on the two pixels and their relative positions. The distance of two pixels of the grid is measured by the length of the minimal path between them. A disk of a grid is a set of pixels such that their distance from a fixed pixel, say P is not greater than a given value. In most of the cases P is considered to be the origin of grid.

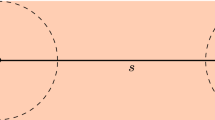
The shape of a disk can be defined as follows. Assume that the pixels of the grid are symmetric and have a center point. Then the shape of the disk is the shape of the convex hull of the center points of the pixels which are the elements of the grid. It is well known that the shape of the disk is always an octagon on the square grid based on the usual two neighborhood [1, 2]. There is a wide variety of shapes of the disks on the triangular grid [8, 12]. On Fig. 1 we show an example.

The pixels of a grid are identified by integer coordinates depending on the type of the grid, e.g., each pixel has its 2 or 3 coordinates which uniquely identify the pixels, in the square and the triangular grids, respectively. These coordinates can be considered as the coordinates of the center point of the pixel. The disk is determined by some inequalities and equations. One inequality restricts the total distance. There are grids where the coordinates must also satisfy some conditions. For example, the sum of the coordinates can be either 0 or 1 in the case of the triangular grid. Finally, the path from the origin to the pixel must be described as well. These constraints are satisfied by many values including even non-integer ones. The problem which is the main topic of this paper is, how can be these constraint used to determine the convex hull of the integer points satisfying the constraints. It is a general problem in integer programming (optimization).

2 The Triangular Grid

Fig. 1.
figure 1

A part of the triangular grid with the symmetric coordinate system, an example to (the convex hull of) a disk and a pixel (X) with its various neighbors (right left corner).

Full size image

The triangular grid is a complete, non-overlapping coverage of the plane by regular triangles [9, 10]. Each pixel of the grid can be addressed by an integer coordinate triplet having zero or one sum. These two types of vectors differentiate the two types of the orientations of the pixels of the grid. Zero sum vectors address the even pixels (they have shape \(\bigtriangleup \) in this paper), while one sum triplets address the odd pixels (their shape is \(\bigtriangledown \)). As Fig. 1 shows, the coordinate axes have angle \(120^\circ \) pairwise. The set of pixels where one of the coordinate values is fixed, is called a lane and it is orthogonal to the axis with fixed value. For example, the pixels of the top of the Fig. 1 belong to the lane \(y=-4\). This symmetric coordinate system captures well the well-known neighborhood relations [3] of the grid (Fig. 1, right). Formally, the points (i.e., pixels) \(p=(p(1),p(2),p(3))\) and \(q=(q(1),q(2),q(3))\) of the triangular grid are

  • m-neighbors (\(m=1,2,3\)), if

    1. (i)

      \(\vert p(i)-q(i)\vert \le 1\), for \(i=1, 2, 3\), and

    2. (ii)

      \(\vert p(1)-q(1)\vert + \vert p(2)-q(2)\vert + \vert p(3)-q(3)\vert \le m.\)

  • strict m-neighbors, if there is an equality in (ii) for the value of m.

Let \(p=(p(1),p(2),p(3))\) and \(q=(q(1),q(2),q(3))\) be two points of the triangular grid. A finite sequence of points of the form \(p=p_0,p_1,\dots ,p_m=q\), where \(p_{i-1}, p_i \) are 3-neighbor points for \(1\le i\le m\), is called a path from p to q. The term k-step will be used to abbreviate the sentence ‘step to a strict k-neighbor point’ (\(k\in \{1,2,3\}\)).

There are three types of steps in the problem which are called according to their length 1-step, 2-step, and 3-step. We use the notation given in Table 1 for various possible k-steps.

Table 1. 1-steps, 2-steps, and 3-steps on the triangular grid.
Full size table

In this paper without loss of generality, we can deal with shortest paths from the origin (0, 0, 0) to point (x, y, z).

Chamfer distances on the triangular grid were investigated in [11] based on various weights for the 3 types of steps on the grid.

3 Chamfer Distances

Using the 3 types of neighbors there could be various paths from a point p to a point q in the triangular grid. Let the weights for the various steps be fixed as a, b, c for 1-, 2-, and 3-steps, respectively, with the condition \(c\ge b \ge a >0\). Then, the sum of the weights of the steps of a path is considered as a weighted path. The chamfer distance (or, in another term, the weighted distance) of two points is the weight of the weighted shortest path between them, i.e., the minimal value among weights of the paths between the points: \(d((x_1,y_1,z_1),(x_2,y_2,z_2);a,b,c)\). In [11] it is proven, that this distance function satisfies the metric conditions: it is positive definite, symmetric and the triangle inequality holds.

Let the chamfer ball, disk(r) be the set of pixels (x, y, z) for which the weighted distance between the origin and (x, y, z) is at most r, formally,

$$\begin{aligned} disk(r)=\{(x,y,z)~|~d((0,0,0),(x,y,z);a,b,c)\le r \}. \end{aligned}$$

Chamfer distances are discussed for some other grid in [13]. They are connected to the Frobenius problem of three variables [4, 13].

4 Integer Hull and Chvátal Cuts

Let m and n be two positive integers, A an \(m\times n\) matrix and b an m-dimensional vector. The set \(P=\{ x\mid Ax\le b\}\) is a polyhedron in the n-dimensional space. The integer hull of P is the convex hull of its integer points, i.e. the set \(int(P)=conv(P\cap Z^n)\), where \(Z^n\) is the lattice of n-dimensional integer vectors.

The set int(P) is not necessarily a polyhedral set [5]. However, it is a polyhedral set in many cases including the case when P is bounded or A and b have rational elements [7]. It means that the disks are always polygons.

The set int(P) can be determined by an iterative procedure. The key tool of the algorithm is the Chvátal cut. Assume that \(\lambda \in \left( \mathbb R^{\ge 0}\right) ^{m}\) is an m-dimensional vector such that the product \(\lambda ^TA\) is an integer vector. Then all integer vector x of P must satisfy the inequality

$$\begin{aligned} \lambda ^TAx\le \left\lfloor \lambda ^Tb\right\rfloor , \end{aligned}$$
(1)

where the usual floor function \(\left\lfloor \cdot \right\rfloor \) is used. If \(\lambda ^Tb\ne \left\lfloor \lambda ^Tb\right\rfloor \) then (1) is not an algebraic consequence of the original inequalities defining P. This inequality is the Chvátal cut which can be added to other inequalities without cutting any integer point from P. Further details of the method can be obtained from [14]. What is important here is that for there are finitely many significantly different Chvátal cuts of every inequality system. One iteration is to generate all of them. When the inequality system is enlarged by the generated inequalities, the procedure can be repeated. The integer hull is obtained after finitely many iterations.

The Chvátal rank of an inequality is the number of the iteration in which it was generated. The rank of the inequalities defining P is 0. The rank of the inequalities generated by rank 0 inequalities is 1, etc. In this paper, only inequalities having rank 1 are investigated. In one iteration the number of Chvátal cuts could be even exponential on the number of original equations (Chap. 23 in [14]), therefore their analysis gives already becomes very time consuming and also gives some nice results. The Chvátal cuts are analyzed systematically only in few papers. [6] discusses the Chvátal cuts of the knapsack polytope of rank 1.

5 Linear Programming Model

There are several methods to describe a chamfer disk. A new approach is discussed in this paper. The polygon of a disk for a given radius r consists of the feasible solutions of an integer programming problem. It means that the coordinate vectors must satisfy certain linear inequalities and must have integer components. The size of the model, i.e. number of rows and columns, is fixed. What is changing is only the right-hand side. The theory of linear programming gives a complete description of the potential optimal solutions. The form of the disks can be one of the elements of a finite set according to our empirical observation. Thus it seems possible to give a complete structural description of the disks by uncovering the integer hull of the feasible sets of the related LP problems. The structural description eliminate the necessity of any algorithm.

A 1-step changes one coordinate by 1 unit. A 2-step changes two coordinates into the opposite direction by 1 unit. Finally, a 3-step changes all coordinates by 1 unit, however the direction of the three changes are not the same. Thus, the matrix of the steps is specified in Table 1. Let \(u_i\), \(v_i\) and \(w_i\) (for \(i=1,\dots ,6\)) are the numbers of various steps. The disk constraint is given in the following form:

$$\begin{aligned} au_1+\cdots +au_6+bv_1+\cdots +bv_6+cw_1+\cdots +cw_6\,\le \,r, \end{aligned}$$

where \(c\ge b \ge a >0\). It should be note here that the triangular grid is not a lattice, therefore the steps of a path are usually not free to permute. However, when a multiset of steps is specified corresponding to a path connecting the origin to another pixel, then because of the constraint on the sum of coordinate values, there exists always a path on the grid which built up by those steps if the sum of the coordinate changes is equal to 0 or 1.

Now, we are ready to continue to show other constraints. All step variables are non-negative:

$$\begin{aligned} u_1,\dots ,u_6,v_1,\dots ,v_6,w_1,\dots ,w_6\,\ge \,0. \end{aligned}$$

If a point \((x,y,z)^T\) is reached from the origin by the steps, then the step numbers satisfy the equation system

$$\begin{aligned} u_1-u_4+v_1+v_2-v_4-v_5+w_1+w_2-w_3-w_4-w_5+w_6= & {} x,\\ u_2-u_5-v_1+v_3+v_4-v_6+w_1-w_2+w_3-w_4+w_5-w_6= & {} y,\\ u_3-u_6-v_2-v_3+v_5+v_6-w_1+w_2+w_3+w_4-w_5-w_6= & {} z. \end{aligned}$$

The sum of the coordinates x, y, and z are between 0 and 1:

$$\begin{aligned} x+y+z\le & {} 1,\\ x+y+z\ge & {} 0. \end{aligned}$$

The polyhedral set is defined by the system of constraints shown in Table 2, where the index of the (in)equality is used in further analysis as is indicated there. Using the same index set, the multipliers of the inequalities of the original constraint set are denoted by \(\lambda _0,\ldots ,\lambda _{23}\), i.e., they are the elements of vector \(\lambda \).

The facet defining inequalities concern to the coordinates of the points only, i.e. to the variables x, y, and z. It is assumed that the facet-defining inequality of the disk is given in the form

$$\begin{aligned} ex+fy+gz\,\le \,h \end{aligned}$$
(2)
Table 2. The inequalities defining the disk polytope, RHS stands for Right-Hand Side.
Full size table

with \(e,f,g,h \in \mathbb Z\). The rank of the defining inequalities is 0 by definition. If (2) is not among the defining inequalities of the disk polytope, then its Chvátal rank is 1 only if multipliers \(\lambda _0,\ldots ,\lambda _{23}\) can be chosen such that \(\lambda _0,\ldots ,\lambda _{18},\lambda _{22},\lambda _{23}\) are nonnegative, and the coefficients on the left-hand side of the generated inequality are e, f, g, 0, ..., 0, while the right-hand side is less than \(h+1\). If there are several options that can be employed to generate the left-hand side, then the preferred choice is that which gives the minimal right-hand side result. This observation leads to the following linear programming model:

$$\begin{aligned} \min \, r\lambda _0+\lambda _{22}&\nonumber \\ -\lambda _{19}+\lambda _{22}-\lambda _{23}= & {} e \end{aligned}$$
(3)
$$\begin{aligned} -\lambda _{20}+\lambda _{22}-\lambda _{23}= & {} f \end{aligned}$$
(4)
$$\begin{aligned} -\lambda _{21}+\lambda _{22}-\lambda _{23}= & {} g \end{aligned}$$
(5)
$$\begin{aligned} a\lambda _0-\lambda _1+\lambda _{19}= & {} 0 \end{aligned}$$
(6)
$$\begin{aligned} \vdots \nonumber \\ a\lambda _0-\lambda _6-\lambda _{21}= & {} 0 \end{aligned}$$
(7)
$$\begin{aligned} b\lambda _0-\lambda _7+\lambda _{19}-\lambda _{20}= & {} 0 \end{aligned}$$
(8)
$$\begin{aligned} \vdots \nonumber \\ b\lambda _0-\lambda _{12}-\lambda _{20}+\lambda _{21}= & {} 0 \end{aligned}$$
(9)
$$\begin{aligned} c\lambda _0-\lambda _{13}+\lambda _{19}+\lambda _{20}-\lambda _{21}= & {} 0 \end{aligned}$$
(10)
$$\begin{aligned} \vdots \nonumber \\ c\lambda _0-\lambda _{18}+\lambda _{19}-\lambda _{20}-\lambda _{21}= & {} 0 \end{aligned}$$
(11)
$$\begin{aligned} \lambda _0, \ldots \lambda _{18}, \lambda _{22}, \lambda _{23}\ge & {} 0. \end{aligned}$$
(12)

6 Construction of Chvátal Cuts

In general, a cut (1) is not necessarily facet defining cut as even stronger cuts might be generated in farther iterations. In this section, some cuts of rank 1 are generated.

The next lemma goes independently of the fact that we are using the triangular grid, that is, we do not take into account about the constraints \(i=22\), 23, we set their weights \(\lambda _{22}=\lambda _{23}=0\).

Lemma 1

Chvátal rank of (2) is 1 if

$$r\cdot \max \left\{ \max \limits _{i\in \{e,f,g\}}\left\{ \frac{|i|}{a}\right\} ; \max \limits _{i,j\in \{e,f,g\}}\left\{ \frac{|i-j|}{b}\right\} ; M_3 \right\} < h+1,$$

where \(M_3 = \max \limits _{i,j,k\in \{e,f,g\}}\left\{ \frac{|i-j-k|}{c};\frac{|i+j-k|}{c}\right\} \).

Proof

If \(\lambda _{22}=\lambda _{23}=0\), then we must minimize \(\lambda _0\) for the best RHS.

In this case from (3), (4), and (5) we get, that \(\lambda _{19}=-e\), \(\lambda _{20}=-f\), and \(\lambda _{21}=-g\).

The minimal value of \(\lambda _0\) for the Eqs. (6) and (7) is

$$\begin{aligned} \frac{\max \{|e|,|f|,|g|\}}{a}=\max \limits _{i\in \{e,f,g\}}\left\{ \frac{|i|}{a}\right\} \le \lambda _0, \end{aligned}$$

because \(\lambda _i\)’s are nonnegative for \(i=1,\dots ,6\).

Similarly, the minimal value of \(\lambda _0\) for the Eqs. (8) and (9) is

$$\begin{aligned} \frac{\max \{|e-f|,|e-g|,|f-g|\}}{b}=\max \limits _{i,j\in \{e,f,g\}}\left\{ \frac{|i-j|}{b}\right\} \le \lambda _0, \end{aligned}$$

because \(\lambda _i\)’s are nonnegative for \(i=7,\dots ,12\).

Finally, the minimal value of \(\lambda _0\) for the Eqs. (10) and (11) is

$$\frac{\max \{|e+f-g|,|e-f+g|,|-e+f+g|\}}{c}= M_3 \le \lambda _0,$$

because \(\lambda _i\)’s are nonnegative for \(i=13,\dots ,18\).    \(\square \)

Corollary 1

If \(2a\le b\), \(3a\le c\) and

$$\begin{aligned} r\cdot \max \limits _{i\in \{e,f,g\}}\left\{ \frac{|i|}{a}\right\} \le h+1, \end{aligned}$$

then the Chvátal rank of (2) is 1.

Theorem 1

Chvátal rank of the inequality \(x\le k\) is 1 if and only if

$$\begin{aligned} \frac{r+a}{2a}<k+1&\;\hbox {if}\;&2a\le b \;\hbox {and}\; 3a\le c,\\ \frac{r+b-a}{b}< k+1&\;\hbox {if}\;&b\le 2a \;\hbox {and}\; 2b\le a+c,\\ \frac{2r+c-a}{c+a} < k+1&\;\hbox {if}\;&c\le 3a \;\hbox {and}\; a+c\le 2b. \end{aligned}$$

Proof

In this case, let \(e=1\), \(f=g=0\) in (2). We need to minimize \(r\lambda _0+\lambda _{22}\), where (3)–(12) hold. Only (3)–(5) contain \(\lambda _{23}\) and always in the form \(\lambda _{22}-\lambda _{23}\) not counting (12). It means that because of minimizing \(\lambda _{22}\) we need to choose \(\lambda _{23}=0\), because \(\lambda _{22}\) is nonnegative. Let us denote \(\lambda _{22}=s\). Thus from (3) we get, that \(\lambda _{19}=s-1\) (it may be negative). From (4) and (5) we get, that \(\lambda _{20}=\lambda _{21}=s\).

Then the minimal value for \(\lambda _0\) satisfies (6) and (7) is the following:

$$\begin{aligned} \frac{\max \{s,-s,s-1,1-s\}}{a}=\max \left\{ \frac{s}{a},\frac{1-s}{a}\right\} \le \lambda _0. \end{aligned}$$
(13)

The minimal value for \(\lambda _0\) satisfies (8)–(9) is

$$\begin{aligned} \frac{\max \{s-s,s-(s-1),(s-1)-s\}}{b}=\frac{1}{b}\le \lambda _0. \end{aligned}$$
(14)

Finally, the minimal value for \(\lambda _0\) satisfies (10)–(11) is

$$\begin{aligned} \frac{\max \{s-s-(s-1),s-s+(s-1),-s-s+(s-1),s+s-(s-1)\}}{c}= \end{aligned}$$
$$\begin{aligned} =\frac{s+1}{c}\le \lambda _0. \end{aligned}$$
(15)

Then from (13)–(15) we get

$$\begin{aligned} \max \left\{ \frac{s}{a},\frac{1-s}{a},\frac{1}{b},\frac{s+1}{c}\right\} \le \lambda _0. \end{aligned}$$

It means that to minimize \(r\lambda _0+s\) we need to minimize the following in s:

$$\begin{aligned} \max \left\{ \frac{rs}{a}+s,\frac{r(1-s)}{a}+s,\frac{r}{b}+s,\frac{r(s+1)}{c}+s\right\} . \end{aligned}$$

There are four functions of s in the above maximum, let us denote them by \(f_1(s), \dots , f_4(s)\).

If \(r<a\), then our disk contains only the origin. We can assume that \(a\le r\). In this case \(f_2(s)\) is decreasing, but other three functions are increasing. If \(s=0\), then the value of the second function is greater than the others: \(f_2(0)=\frac{r}{a}\ge f_i(0)\), where \(i=1,3,4\), because we assumed that \(a\le b\le c\).

The minimal value of the maximum of the above functions is obtained when the decreasing one (\(f_2(s)\)) has the same value as one of the increasing functions (we say that the decreasing function and one of the increasing functions are intersecting each other).

Case 1. The intersection of \(f_1(s)\) and \(f_2(s)\) is \(s=\frac{1}{2}\). In this case the value of the functions is

$$\begin{aligned} f_1\left( \frac{1}{2}\right) =f_2\left( \frac{1}{2}\right) =\frac{r+a}{2a}. \end{aligned}$$

It is maximal for all \(f_i\) in \(s=\frac{1}{2}\) if \(f_1(s)=f_2(s)\ge f_3(s)\), thus

$$\begin{aligned} \frac{r}{2a}+\frac{1}{2}\ge \frac{r}{b}+\frac{1}{2}, \end{aligned}$$

and this holds if \(2a\le b\). \(f_1(s)=f_2(s)\ge f_4(s)\) means that

$$\begin{aligned} \frac{r}{2a}+\frac{1}{2}\ge \frac{\frac{3}{2}r}{c}+\frac{1}{2}, \end{aligned}$$

and this holds if \(3a\le c\).

Case 2. The intersection of \(f_2(s)\) and \(f_3(s)\) is \(s=\frac{b-a}{b}\) from \(\frac{1-s}{a}=\frac{1}{b}.\) In this case the value of the functions is

$$\begin{aligned} f_2\left( \frac{b-a}{b}\right) =f_3\left( \frac{b-a}{b}\right) =\frac{r+b-a}{b}. \end{aligned}$$

It is maximal for all \(f_i\) in \(s=\frac{b-a}{b}\) if \(f_2(s)=f_3(s)\ge f_1(s)\), thus

$$\begin{aligned} \frac{r}{b}+\frac{b-a}{b}\ge \frac{r(b-a)}{ba}+\frac{b-a}{b}, \end{aligned}$$

and this holds if \(b\le 2a\). \(f_2(s)=f_3(s)\ge f_4(s)\) means that

$$\begin{aligned} \frac{r}{b}+\frac{b-a}{b}\ge \frac{r(2b-a)}{bc}+\frac{b-a}{b}, \end{aligned}$$

and this holds if \(2b\le a+c\).

Case 3. The intersection of \(f_2(s)\) and \(f_4(s)\) is \(s=\frac{c-a}{c+a}\) from \(\frac{1-s}{a}=\frac{s+1}{c}.\) In this case the value of the functions is

$$\begin{aligned} f_2\left( \frac{c-a}{c+a}\right) =f_4\left( \frac{c-a}{c+a}\right) =\frac{2r+c-a}{c+a}. \end{aligned}$$

It is maximal for all \(f_i\) in \(s=\frac{c-a}{c+a}\) if \(f_2(s)=f_4(s)\ge f_1(s)\), thus

$$\begin{aligned} \frac{2r}{c+a}+\frac{c-a}{c+a}\ge \frac{r(c-a)}{a(c+a)}+\frac{c-a}{c+a}, \end{aligned}$$

and this holds if \(c\le 3a\). \(f_2(s)=f_4(s)\ge f_3(s)\) means that

$$\begin{aligned} \frac{2r}{c+a}+\frac{c-a}{c+a}\ge \frac{r}{b}+\frac{c-a}{c+a}, \end{aligned}$$

and this holds if \(a+c\le 2b\).    \(\square \)

The conditions of the above three cases contain all possibilities. If \(2a\le b\) and \(3a\le c\), then this is Case 1. If \(b\le 2a\) and \(3a\le c\), then \(2b\le 4a\le a+c\), thus this subcase is part of Case 2. If \(2a\le b\) and \(c\le 3a\), then \(c+a\le 4a\le 2b\), thus this subcase is part of Case 3. If \(b\le 2a\) and \(c\le 3a\), then \(a+c\le 2b\) or \(2b\le a+c\) is possible, thus one part of this subcase belongs to Case 2, another part of this subcase belongs to Case 3. Further we will refer to these cases as we have described them here.

Theorem 2

Chvátal rank of the inequality \(-x\le l\) is 1 if and only if

$$\begin{aligned} \frac{r}{2a}< l+1&\;\hbox {if}\;&2a\le b \;\hbox {and}\; 3a\le c,\\ \frac{r}{b}< l+1&\;\hbox {if}\;&b\le 2a \;\hbox {and}\; 2b\le a+c,\\ \frac{2r}{c+a} < l+1&\;\hbox {if}\;&c\le 3a \;\hbox {and}\; a+c\le 2b. \end{aligned}$$

The proof follows the same idea as the previous one with \(e=-1\), \(f=g=0\) in (2).

7 Facet-Defining Inequalities

Theorem 3

The above mentioned inequalities \(x\le k\) and \(-x\le l\) are facet-defining in Case 1 and in Case 2.

Proof

Case \(2a\le b\) and \(3a\le c\). This case belongs to Case 1 of the above two Theorems. It is in [11] that the distance function between (0, 0, 0) and (x, y, z) is \(d(a,b,c)=a(|x|+|y|+|z|)\). If we want to create the point of the disk, which has minimal or maximal value in x, we need to solve the following problem:

$$\begin{aligned} \min (\hbox {or} \max ) x&\nonumber \\ d(a,b,c)\le & {} r \end{aligned}$$
(16)
$$\begin{aligned} x+y+z\le & {} 1\\ -x-y-z\le & {} 0\\ x,y,z\in & {} \mathbb Z \end{aligned}$$

If \(x+y+z=0\), then the maximal value of |x| can be equal to \(\frac{|x|+|y|+|z|}{2}\). In this case \(2|x|=|x|+|y|+|z|\le \frac{r}{a}\) and it means that \(-x\le \left\lfloor \frac{r}{2a}\right\rfloor \) is a facet-defining equation.

If \(x+y+z=1\), then the maximal value of x can be equal to \(\frac{|x|+|y|+|z|+1}{2}\). In this case \(2x-1=|x|+|y|+|z|\le \frac{r}{a}\) and \(x\le \left\lfloor \frac{r+a}{2a}\right\rfloor \) is a facet-defining equation.

Case \(b\le 2a\) and \(3a\le c\). In this case \(2b\le a+c\), and this case belongs to Case 2 of the above two Theorems. The distance function between (0, 0, 0) and (x, y, z) is in [11]:

$$d(a,b,c)=\left\{ \begin{array}{ll} b\frac{|x|+|y|+|z|}{2}, &{} \hbox {if}\;x+y+z=0; \\ a+b\frac{|x|+|y|+|z|-1}{2}, &{} \hbox {if}\;x+y+z=1. \end{array} \right. $$

If \(x+y+z=0\), then from (16) and from the maximal value of |x| we get that \(2|x|=|x|+|y|+|z|\le \frac{2r}{b}\) and it means that \(-x\le \left\lfloor \frac{r}{b}\right\rfloor \) is a facet-defining equation.

If \(x+y+z=1\), then from (16) and from the maximal value of x we get that \(2x-1=|x|+|y|+|z|\le \frac{2r-2a+b}{b}\) and \(x\le \left\lfloor \frac{r+b-a}{b}\right\rfloor \) is a facet-defining equation.

Case \(b\le 2a\), \(c\le 3a\) and \(a+b\le c\). In this case \(2b\le a+c\), and this case belongs to Case 2. In this case function d is the same as in the previous case, i.e., our statements hold.

Case \(b\le 2a\), \(c\le 3a\), \(c\le a+b\) and \(2b\le a+c\). This case belongs to Case 2, too. If \(x+y+z=0\), then function d is the same as in the previous case. If \(x+y+z=1\) and we want to maximize the value of |x|, then x is positive and y and z are negative. In this case [11] uses the same distance function as in the previous case. There is a third distance function in [11] in the case of \(x+y+z=1\) for the subcase a negative and two positive coordinates, but in this subcase the value of |x| is not maximal.

Case \(b\le 2a\), \(c\le 3a\), \(c<a+b\) and \(a+c\le 2b\) and Case \(2a\le b\) and \(c\le 3a\).

These cases belong to Case 3.    \(\square \)

The result of the theorem can give at most 6 of the sides of the chamfer disk, that is, actually, the embedded hexagon of the disk.

Example. The inequalities provided by the theorem can be both facet defining and non-facet defining in Case 3. If \(a=4\), \(b=7\), \(c=8\) and \(r=30\) (see Fig. 1), then this case belongs to Case 3.

(a) In this case the Chvátal rank of the inequality of \(-x\le l\) is 1 if and only if \(\left\lfloor \frac{60}{12}\right\rfloor =5\le l\). Let v(i) be the sorted coordinate values of (x, y, z) in a non-increasing way by their absolute values, i.e., \(|v(3)|\le |v(2)|\le |v(1)|\). The distance function between (0, 0, 0) and (x, y, z) is in [11]:

$$\begin{aligned} {} d(a,b,c)=|v(1)|\frac{b}{2}+|v(2)|\frac{b}{2}+|v(3)|(a+c-\frac{3}{2}b), \end{aligned}$$
(17)

if \(x+y+z=0\). In this case \(a+c-\frac{3}{2}b\le \frac{b}{2}\), thus the value of d(a, b, c) is minimal for a given x if |v(3)| is close to |v(2)|, i.e., if x is even, then \(|v(2)|=|v(3)|=\frac{|x|}{2}\); and if x is odd, then \(|v(2)|=|v(3)|+1=\frac{|x|+1}{2}\). For example if \((x,y,z)=(-5,3,2)\), then \(v(1)=-5\), \(v(2)=3\), \(v(3)=2\), and in this case \(d(4,7,8)=31\), thus there is no point with \(x=-5\) for this distance function to satisfy \(d(.)\le r\).

If \(x+y+z=1\), then the distance function between (0, 0, 0) and (x, y, z) is different from (17). If \(x+y+z=1\) and \(x=-5\), then by decreasing one of the positive coordinates by 1, the new point has the same x value and the distance of the new point from (0, 0, 0) is less than the distance of the original one, thus there is no point with \(x=-5\) for the distance functions of case \(x+y+z=1\) to satisfy \(d(.)\le r\). It means that the disk of the value \(r=30\) has no point with \(x=-5\), i.e., \(-x\le 5\) is not facet-defining.

(b) The Chvátal rank of the inequality of \(x\le 5\) is 1. If \((x,y,z)=(5,-1,-3)\), then \(d(4,7,8)=30\) based on [11], thus \(x\le 5\) is a facet-defining equation.

(c) \((5,-1,-3)\) and \((4,1,-4)\) are points of the disk, the inequality \(x-z\le 8\) holds for these pixels of the disk. The Chvátal rank of this inequality is 1 if \(h=8\) in Lemma 1, thus \(x-z\le 8\) is a facet-defining equation with Chvátal rank of 1.

The disk of Fig. 1 has 12 facet-defining equation: there are three 1-ranked inequalities similar to \(x\le 5\); six 1-ranked inequalities similar to \(x-z\le 8\); and three not 1-ranked inequalities similar to \(-x\le 4\).

A further analysis of 1-ranked conditions is planned. We believe that we will find connection between the chamfer radius of the disk and the Eucledian radius by using the theory of 1-ranked conditions.