Abstract
Low-frequency gyrotropic dynamics (100 MHz range) in clusters of interacting magnetic vortex state dots are considered. The clusters consist of 3 or 4 laterally placed cylindrical ferromagnetic dots on a dielectric substrate in the form of equilateral triangles or squares. The interdot dynamical magnetostatic interactions are considered in the form of explicit multipole decompositions on the inverse dot center-to-center distance. The eigenfrequencies of collective magnetic vortex oscillations are calculated analytically and compared with the results of recent experiments conducted on clusters of permalloy dots.
Export citation and abstract BibTeX RIS
Patterned magnetic films in the form of regular arrays of small flat particles (dots) with different shapes are considered as artificial magnetic nanostructures, which are actively investigated nowadays. The isolated ferromagnetic dots reveal discrete spin excitation spectra due to geometrical confinement.1) The interdot coupling (pure magnetostatic, if the ferromagnetic dots are put on a dielectric substrate) leads to collective spin excitation spectra of the dot lattices (magnonic crystals) or dot clusters. The standard Bloch approach along with the periodic Born–von Karman boundary conditions2) can be applied to describe the eigenfunctions and eigenfrequencies of magnonic crystals within momentum representation introducing a quasi-continuous Bloch wave vector.3) However, the excitation spectra of small clusters consisting of N magnetostatically coupled dots (typically, N ≤ 9) can be considered only in the coordinate representation.4,5) It was found6) that these spectra are analogous to the lattice vibration spectra of N-atomic molecules bound with dipolar interactions.
The lateral arrays of soft magnetic dots with submicron and micron in-plane sizes attract extra attention owing to the presence of a vortex (topological soliton) magnetization configuration in their ground states.7) The vortices are characterized by in-plane curling magnetization in the main dot area and a small vortex core with the perpendicular magnetization bearing a topological charge. The vortex core excited by an external magnetic field or a spin-polarized electric current can oscillate in the 100 MHz–1 GHz range (gyrotropic modes) providing a small frequency linewidth and a relatively high microwave power output.8) The vortex oscillators coupled to each other are now under intensive investigation as promising candidates for spin-torque nano-oscillators emitting microwaves or transferring the microwave signals in magnonic crystals.9) One of the unresolved problems is the synchronization of several coupled nano-oscillators to increase essentially the generated microwave power. Recently, clusters of the coupled vortex state dots have been proposed as efficient bipolar junction transistors.10) The need of close packing of such magnetic dots to increase interdot magnetostatic interactions leads to the necessity of considering the collective vortex dynamics in dot pairs and clusters. The simplest case of vortex gyrotropic excitation in a dot pair was considered theoretically in Refs. 4 and 5.
The effect of the interdot interaction on the ferromagnetic resonance spectra of closely packed rectangular lattices of ferromagnetic dots was explored for the first time by Kakazei et al.11) A series of experimental and theoretical papers on the coupled magnetic vortex dynamics in lateral nanostructures have been published recently. Two-dimensional (2D) arrays, chains, and clusters of the circular and square (rectangular) dots were investigated theoretically12) and by different experimental techniques, such as broadband ferromagnetic resonance,13–16) Brillouin light scattering,17) and time-resolved X-ray imaging.18–20) In this letter, we present an analytical approach to the problem of excitation spectra of coupled magnetic vortex dots if the number of dots is more than 2 and they form a cluster. The collective eigenfrequencies are explicitly calculated for triangular (N = 3) and square (N = 4) dot clusters, and their dependence on interdot separation is represented via analytic expressions for magnetostatic coupling integrals.
For the consideration of magnetization dynamics in coupled vortex dot arrays, we use a theoretical approach based on the Landau–Lifshitz (LL) equation of magnetization (M) motion, 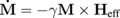 , where
, where  , w being the magnetic energy density. It is convenient to rewrite the LL equation of motion of dot magnetizations,
, w being the magnetic energy density. It is convenient to rewrite the LL equation of motion of dot magnetizations, 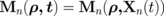 , in the form of Thiele equations of motion21) for the vortex core positions
, in the form of Thiele equations of motion21) for the vortex core positions 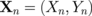 in the n-th dot via the complex variables
in the n-th dot via the complex variables 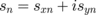 ,
, 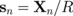 :
:

where 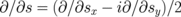 ,
,  ,
,  , and
, and 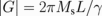 are the z-projection and absolute value of the gyrovector of the n-th dot in the array, L is the dot thickness, R is the dot radius,
are the z-projection and absolute value of the gyrovector of the n-th dot in the array, L is the dot thickness, R is the dot radius, 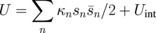 is the total magnetic energy of the vortex dot array,
is the total magnetic energy of the vortex dot array, 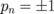 is the vortex core polarization, and κn is the stiffness coefficient22) of the n-th dot. The dots are assumed to be sufficiently thin (L < 50 nm). Therefore, the dependence of the dot magnetization on the thickness coordinate (z) can be neglected. We are interested in finding eigenfrequencies of the coupled vortex state dots in the positions described by the in-plane vector
is the vortex core polarization, and κn is the stiffness coefficient22) of the n-th dot. The dots are assumed to be sufficiently thin (L < 50 nm). Therefore, the dependence of the dot magnetization on the thickness coordinate (z) can be neglected. We are interested in finding eigenfrequencies of the coupled vortex state dots in the positions described by the in-plane vector 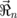 ; therefore, the damping term is not included in Eq. (1).
; therefore, the damping term is not included in Eq. (1).
Equation (1) using the interaction energy calculated in Ref. 12,
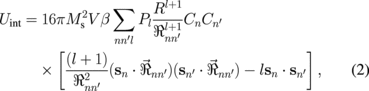
where 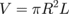 is the dot volume,
is the dot volume, 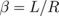 , Pl are the coefficients of multipole decomposition,
, Pl are the coefficients of multipole decomposition, 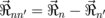 , and
, and 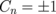 are the vortex chiralities,7) can be applied to consider the coupled vortex dynamics in small dot clusters consisting of cylindrical dots
are the vortex chiralities,7) can be applied to consider the coupled vortex dynamics in small dot clusters consisting of cylindrical dots 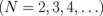 . Equation (2) is obtained from the multipole decomposition of the dot pair interaction energy. The dot multipole moments
. Equation (2) is obtained from the multipole decomposition of the dot pair interaction energy. The dot multipole moments 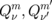 (
(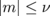 , the index
, the index 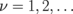 ) are not zero only for odd
) are not zero only for odd 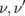 ; therefore, the index
; therefore, the index 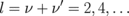 is even.12) The anisotropic interdot interaction (2) breaks the circular dot symmetry, and the eigenmodes correspond to elliptical vortex core trajectories.5)
is even.12) The anisotropic interdot interaction (2) breaks the circular dot symmetry, and the eigenmodes correspond to elliptical vortex core trajectories.5)
The system of the coupled Thiele equations of motion (1) after conducting the Fourier transform 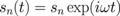 is reduced to pairs of conjugated equations (κn = κ for identical dots),
is reduced to pairs of conjugated equations (κn = κ for identical dots),
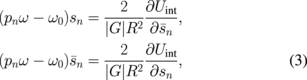
where 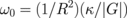 .
.
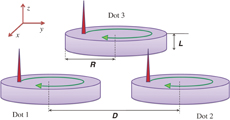
The problem is reduced to the calculation of the interdot interaction energy Uint accounting for the geometry of the dot clusters. We consider the clusters with the numbers of identical dots, i.e., N = 3 [the dots are placed in the vertexes of the equilateral triangle in the xOy plane (Fig. 1)] and N = 4 (the dots are placed in the vertexes of a square).
Fig. 1. Cluster of three magnetic vortex state cylindrical dots. The dot radius is R, the thickness is L, and the center-to-center interdot distance is D.
Download figure:
Standard image High-resolution imageThe vortex chiralities do not change the fine structure of the excitation spectra keeping the values of the eigenfrequencies; they change only the symmetry of the eigenmodes belonging to each eigenfrequency.23) The set of vortex core polarizations for the dot array, {pn}, is of principal importance for calculations of the eigenfrequencies. Therefore, the excitation spectrum is determined by the choice of a particular {pn} set. In the cluster of N dots, the number of eigenfrequencies is N; however, the number of nonequivalent sets of core polarizations is essentially smaller than 2N. The core polarizations can be easily controlled by applying and releasing a perpendicular bias magnetic field. No simple means exist to control the chirality of the circular dots. Fortunately, in the case of linear vortex dynamics, the vortex chiralities can be excluded from the equations of motion using the relation 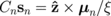 ,7) where
,7) where 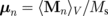 is the n-th dot volume average magnetization, and the model-dependent parameter ξ is on the order of 1 (ξ = 2/3 for the two-vortex model of the displaced vortex7)). The interdot interacting energy
is the n-th dot volume average magnetization, and the model-dependent parameter ξ is on the order of 1 (ξ = 2/3 for the two-vortex model of the displaced vortex7)). The interdot interacting energy
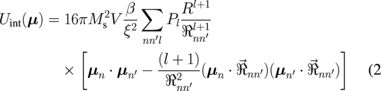
allows writing the equations of motion of the dot average magnetization (μn) in the form similar to the LL equation (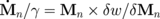 ) as
) as
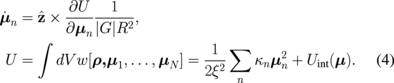
The eigenmodes of the linear Eq. (4) in terms of μn do not depend on the vortex chiralities. If one only wants to recalculate the eigenmodes to elementary motions of the vortex core coordinates (Sn) in each dot, then one needs to specify the set of chiralities (Cn). In many practical cases, the μn representation is sufficient because it allows us to determine which eigenmodes can be excited by the in-plane magnetic field of a given direction (the total mode dynamical magnetization should not be zero in that direction) and what their relative intensities are.
Let us consider first the cluster of N = 3 dots placed in the vertexes of the equilateral triangle. Applying the equations of motion (3) with the interdot interaction energy given by Eq. (2), we can calculate the eigenfrequencies analytically. We need to find the eigenvalues and the eigenvectors of the dynamical matrix corresponding to the system of equations of motion (3), which can be written in the standard form  . The nondiagonal components of the matrix
. The nondiagonal components of the matrix 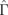 are determined by the interdot magnetostatic coupling, and the vector
are determined by the interdot magnetostatic coupling, and the vector 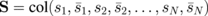 is composed of dot variables
is composed of dot variables 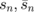 . The matrix elements of
. The matrix elements of  and the frequency ω are normalized to the gyrotropic frequency of the isolated dot, ω0, which is
and the frequency ω are normalized to the gyrotropic frequency of the isolated dot, ω0, which is 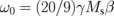 for the dot aspect ratio β = L/R ≪ 1. The secular equation for the eigenfrequencies,
for the dot aspect ratio β = L/R ≪ 1. The secular equation for the eigenfrequencies, 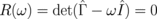 , is cubic with respect to ω2:
, is cubic with respect to ω2:
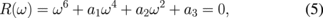
where the coefficients are: 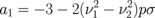 ,
, 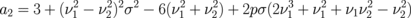 ,
, 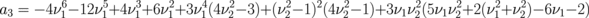 ,
, 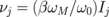 ,
,  ,
, 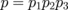 , and
, and 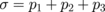 .
.
The interdot coupling integrals [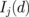 ] are (
] are (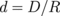 )
)
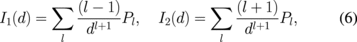
where
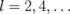 and we considered that, for the dot cluster, all interdot center-to-center distances are equal, namely,
and we considered that, for the dot cluster, all interdot center-to-center distances are equal, namely, 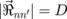 .
.
The expressions for the eigenfrequencies are complicated. Therefore, we present these eigenfrequencies in the limit of weak interdot coupling, 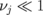 (the coupling energy is typically lower than 10% of the in-dot magnetic energy). The eigenfrequencies are functions of two combinations of vortex core polarizations, p and σ. Thus, we have two different cases of vortex motion: all polarizations are parallel (p = +1 or p = − 1, σ = ±3), all cores move counterclockwise (σ = +3) or clockwise (σ = −3), and two polarizations are parallel, one is antiparallel to them (
(the coupling energy is typically lower than 10% of the in-dot magnetic energy). The eigenfrequencies are functions of two combinations of vortex core polarizations, p and σ. Thus, we have two different cases of vortex motion: all polarizations are parallel (p = +1 or p = − 1, σ = ±3), all cores move counterclockwise (σ = +3) or clockwise (σ = −3), and two polarizations are parallel, one is antiparallel to them (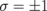 ,
, 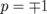 ). The parameters p and σ are related by the equation
). The parameters p and σ are related by the equation 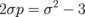 . There are two sets of three eigenfrequencies of the dot cluster, and these sets depend on σ2. The values ±σ correspond to the same eigenfrequencies; therefore, we can choose σ > 0 and distinguish the eigenfrequency sets using the parameter p = ±1. In the case of p = +1, the vortex eigenfrequencies are
. There are two sets of three eigenfrequencies of the dot cluster, and these sets depend on σ2. The values ±σ correspond to the same eigenfrequencies; therefore, we can choose σ > 0 and distinguish the eigenfrequency sets using the parameter p = ±1. In the case of p = +1, the vortex eigenfrequencies are
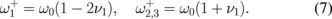
It is easy to calculate the coupling integrals [Ij(d)] defined by Eq. (6). The parameters (Pl) of the integrals in the multipole decomposition (6) are model-dependent. For the two-vortex model of the displaced vortex core, we obtain  ,
, 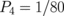 ,
, 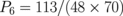 , ..., see Ref. 12. The term with l = 2 corresponds to dipole–dipole, that with l = 4 corresponds to dipole–octupole, and that with l = 6 corresponds to octupole–octupole and dipole–triacontedipole interdot magnetostatic coupling of the dot multipole moments. The l = 2 term is the main term in the multipole decomposition (6) at large and moderate d > 2.5; however, for
, ..., see Ref. 12. The term with l = 2 corresponds to dipole–dipole, that with l = 4 corresponds to dipole–octupole, and that with l = 6 corresponds to octupole–octupole and dipole–triacontedipole interdot magnetostatic coupling of the dot multipole moments. The l = 2 term is the main term in the multipole decomposition (6) at large and moderate d > 2.5; however, for 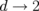 , the high-order multipole terms are important.
, the high-order multipole terms are important.
In the case of p = −1, the vortex eigenfrequencies are
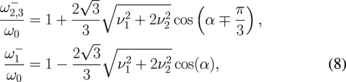
where the angle α is determined by the expression 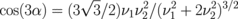 .
.
To calculate the eigenfrequencies of the cluster consisting of N = 4 dots, we introduced 4 coupling integrals, corresponding to the interaction of the x- and y-components of the dynamical magnetizations (μn) of the dots located on the square side and square diagonal,  and
and 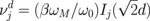 , respectively. The secular equation
, respectively. The secular equation 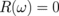 is complicated. However, for physically interesting cases of aligned vortex core polarizations (all pn = +1 or −1) and checkerboard ordering of the polarizations (p1 = p3 = +1, p2 = p4 = −1, the cluster ground state), it reduces to bilinear and biquadratic equations and has a simple solution. By using the smallness of the coupling parameters
is complicated. However, for physically interesting cases of aligned vortex core polarizations (all pn = +1 or −1) and checkerboard ordering of the polarizations (p1 = p3 = +1, p2 = p4 = −1, the cluster ground state), it reduces to bilinear and biquadratic equations and has a simple solution. By using the smallness of the coupling parameters 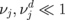 , the eigenfrequencies can be written for pn = +1 as
, the eigenfrequencies can be written for pn = +1 as
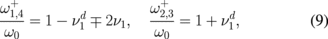
and for p1 = p3 = +1 and p2 = p4 = −1 as
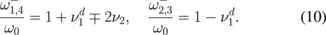
All the eigenfrequencies (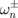 ) increase with the number n and satisfy the equation
) increase with the number n and satisfy the equation 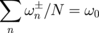 . The frequency splitting between the gyrotropic eigenfrequencies is determined by the parameter νj. In the limit of thin dots, β ≪ 1,
. The frequency splitting between the gyrotropic eigenfrequencies is determined by the parameter νj. In the limit of thin dots, β ≪ 1, 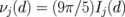 depends only on the interdot distance d, i.e., the frequency splitting in thin dots in relative units depends only on d, whereas in absolute units (MHz), the splitting is also proportional to β. We explicitly obtain
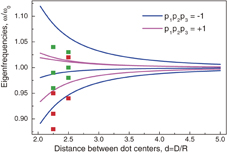
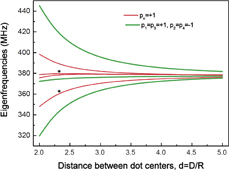
depends only on the interdot distance d, i.e., the frequency splitting in thin dots in relative units depends only on d, whereas in absolute units (MHz), the splitting is also proportional to β. We explicitly obtain 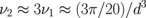 within the dipole–dipole approximation. The calculated eigenfrequencies of the dot clusters with different sets of {pn} are shown in Figs. 2 and 3. The degenerated gyrotropic frequency ω0 splits into several eigenfrequencies (fine structure of the spectra) owing to the interdot interaction, and the splitting increases with decreasing lateral distance d between the dot centers. The frequency splitting is essentially larger in the case of unaligned vortex core polarization of dots forming a cluster. For the N = 3 cluster (p = −1), the lowest
within the dipole–dipole approximation. The calculated eigenfrequencies of the dot clusters with different sets of {pn} are shown in Figs. 2 and 3. The degenerated gyrotropic frequency ω0 splits into several eigenfrequencies (fine structure of the spectra) owing to the interdot interaction, and the splitting increases with decreasing lateral distance d between the dot centers. The frequency splitting is essentially larger in the case of unaligned vortex core polarization of dots forming a cluster. For the N = 3 cluster (p = −1), the lowest 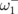 and highest
and highest 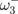 eigenfrequencies determine the total frequency splitting. For the N = 4 dot cluster, the spectrum consists of two double-degenerated frequencies (
eigenfrequencies determine the total frequency splitting. For the N = 4 dot cluster, the spectrum consists of two double-degenerated frequencies (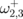 ) and two frequency doublets (
) and two frequency doublets (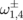 ). There is a degenerated frequency (
). There is a degenerated frequency (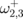 ) for 3- and 4-dot clusters, which splits only in the limit of touching dots,
) for 3- and 4-dot clusters, which splits only in the limit of touching dots, 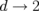 , when nonlinear coupling terms become important in the eigenfrequency decompositions (7) and (9). The eigenfrequency
, when nonlinear coupling terms become important in the eigenfrequency decompositions (7) and (9). The eigenfrequency 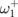 is essentially lower than
is essentially lower than 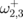 and decreases with decreasing d for N = 3 and 4. The eigenfrequency
and decreases with decreasing d for N = 3 and 4. The eigenfrequency 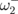 (N = 3) and the double-degenerated frequency
(N = 3) and the double-degenerated frequency 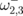 (N = 4) depend very weakly on the interdot separation. Owing to the relation
(N = 4) depend very weakly on the interdot separation. Owing to the relation 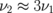 , the overall frequency splitting of the initially degenerated frequency ω0 of the 4-dot cluster is essentially larger for
, the overall frequency splitting of the initially degenerated frequency ω0 of the 4-dot cluster is essentially larger for 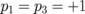 and
and 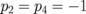 . The frequency spectra of the N = 3 and 4 clusters are similar in the case of antiparallel vortex core polarization.
. The frequency spectra of the N = 3 and 4 clusters are similar in the case of antiparallel vortex core polarization.
Fig. 2. Gyrotropic eigenfrequencies of three vortex dot clusters (N = 3). The dot centers form an equilateral triangle; the symbols correspond to the frequencies measured in Ref. 19 by PEEM. Red (green) symbols: the excitation field is directed parallel (perpendicular) to the triangle base.
Download figure:
Standard image High-resolution imageFig. 3. Gyrotropic eigenfrequencies of four vortex dot clusters (N = 4). The dot centers form a square [aligned and chessboard vortex core polarizations (pn)], Ms = 630 G, β = 0.1. Different vortex core polarizations (pn) are marked. Stars mark the frequency spread measured by broadband ferromagnetic resonance in Ref. 14.
Download figure:
Standard image High-resolution imageIn the recent experiment by Wang et al.,19) the excitation frequencies of the triangle permalloy (NiFe alloy) vortex dot clusters were measured by time-resolved photoemission electron microscopy (PEEM) imaging. The dot thickness L was 30 nm, the radius R was 2 µm (β = 0.015, ω0/2π = 71 MHz), and the dot center-to-center distance D was 4.5–5.0 µm (d = 2.25–2.50). The relatively large bandwidths of the splitted eigenfrequencies, 0.16ω0 for d = 2.25 and 0.09ω0 for d = 2.50, indicate that the vortex core polarizations in the dot clusters are antiparallel (p = −1). The results of the experiments are compared with those of the calculations using Eqs. (5) and (6) in Fig. 2. The agreement is good, especially considering that the accuracy in the frequency measurements would be about 10% if only two periods of dot magnetization oscillations after excitation by an in-plane field pulse were detected. This initial stage of vortex motion in each dot was fitted using a sinusoidal function with only one dominating frequency, which does not generally match any of the dot cluster eigenfrequencies.19) The dominating frequencies are shown in Fig. 2 by symbols. The dominating frequencies are close to the frequency of the maximum of the function of intensity,  , versus the frequency ω for a given excitation field direction. The eigenmode with the lowest eigenfrequency
, versus the frequency ω for a given excitation field direction. The eigenmode with the lowest eigenfrequency 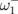 [see Eq. (8)] having the maximal average magnetization along the field is excited by the field pulse directed parallel to the triangle base. On the other hand, the eigenmode with the eigenfrequency
[see Eq. (8)] having the maximal average magnetization along the field is excited by the field pulse directed parallel to the triangle base. On the other hand, the eigenmode with the eigenfrequency 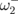 is excited by the field pulse directed perpendicularly to the triangle base, i.e., the red (green) squares in Fig. 2 are just three different estimations of the eigenfrequency
is excited by the field pulse directed perpendicularly to the triangle base, i.e., the red (green) squares in Fig. 2 are just three different estimations of the eigenfrequency 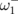 (
(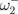 ) in the PEEM experiment.19)
) in the PEEM experiment.19)
In the study by Vogel et al.,14) the vortex frequencies were measured for different sizes of dot arrays using the broadband ferromagnetic resonance and varying the interdot distance d from 2.15 to 4.12.14) The resonance linewidth is larger than the frequency splitting, and the fine structure of the spectra is not resolved. Therefore, it is reasonable to introduce a frequency spread due to the interdot coupling as the difference in resonance linewidth between the interacting and isolated dots (β = 0.1, ω0/2π = 378 MHz). For 2 × 2 circular dot arrays (N = 4 clusters), the measured frequency spread was approximately 20 MHz for d = 2.32. This spread is around the frequency of 372 MHz corresponding to the resonance signal intensity maximum. The results of the ferromagnetic resonance experiments14) are compared with those of calculations using Eqs. (9) and (10) for the N = 4 cluster in Fig. 3. We calculated the maximum frequency spreads of 41 MHz (d/R = 2.15) and 30 MHz (d/R = 2.32) for the same core polarization, and 102 MHz (d/R = 2.15) and 77 MHz (d/R = 2.32) for the chessboard ordering of the vortex core polarizations. Considering that the vortex core polarization set {pn} was not especially prepared/controlled, the agreement with the experiment14) is quite good. Most probably, the core polarizations of the square dot clusters measured in Ref. 14 are aligned (all pn = +1 or −1).
Very recently, Haenze et al.20) have measured coupled vortex modes for the N = 9 dot cluster by scanning transmission X-ray microscopy. For such a large cluster, there are approximately 100 nonequivalent configurations of the vortex core polarizations ({pn}), and nine, in general, different eigenfrequencies. However, it was shown directly that a stripe pattern consisting of columns (rows) of alternative core polarizations was established in the cluster that essentially simplifies the description of the dynamics. For larger dot clusters (N > 9) of square/rectangular shape, the coordinate approach is very complicated, and we can use the momentum representation12) with the discrete wave vector k, where its components kx and ky are chosen within the first Brillouin zone 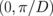 . The eigenfrequencies are then determined using Eq. (23) of Ref. 12 as
. The eigenfrequencies are then determined using Eq. (23) of Ref. 12 as 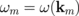 . The choice of the discrete values of km and the corresponding standing waves of the dot magnetization
. The choice of the discrete values of km and the corresponding standing waves of the dot magnetization 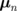 oscillations as a function of the set of {pn} is beyond the scope of this study and will be considered elsewhere.
oscillations as a function of the set of {pn} is beyond the scope of this study and will be considered elsewhere.
In summary, the low-frequency gyrotropic dynamics in clusters of 3 or 4 laterally placed magnetic vortex state cylindrical dots were considered. The eigenfrequencies of collective vortex oscillations were calculated analytically and compared with the results of recent broadband ferromagnetic resonance and X-ray imaging experiments. The fine structures of the spectra of N = 3 and 4 dot clusters are similar. The splitting of the degenerated gyrotropic frequency of isolated dots was determined by interdot coupling integrals, which are expressed explicitly in the form of multipole decomposition. The fine structure of the dot spectra can be tuned by changing the vortex core polarizations by an external magnetic field. The spread of the collective mode frequencies is approximately 3 times larger for the antiparallel vortex core polarization than for the aligned case. The accuracy of the current experimental techniques is insufficient to clearly detect the fine structure of the spectra of the cluster-forming coupled vortex dots (the frequency splitting is about 10–30 MHz). This can be a research subject in the near future.
Acknowledgments
K.G. acknowledges support from IKERBASQUE (the Basque Foundation for Science). This work was partially supported by Spanish MINECO Grant No. FIS2010-20979-C02-01. O.S. acknowledges financial support from the University of the Basque Country UPV/EHU.