Abstract

Keywords

Fast Fourier Transform (FFT), Multi-Assets, Finite and Infinite Dimension of Assets, Economic Recession, Volatility Change, European Options

Share and Cite:

1. Introduction

In the history of options valuation, the work of Black-Scholes [1] (1973) cannot be forgotten no matter the shortcomings we may find in their work such as the issue of constant values assumed by the volatility and interest rates. Divers financial assets are traded in financial market. Some are risky assets while some are riskfree. Multi-asset options generally are a set of options whose pay-offs are governed by more than one underlying assets. A typical example of multi-asset option is a basket option. Basket option is based on two or more underlying assets or stocks. There is European type basket call or put option whereby the overall value of a basket of assets plays the role of the price of the underlying asset in single-asset European. Likewise, we have American style basket options as well. Other types of multi-assets options include: spread option, exchange options, Quanto options, Rainbow options, etc. Various types of multi-asset options could be described based on their payoff function. Beom, J. K. et al. (2013) [2] presents a simple numerical approach for American put options valuation.

The focus of most researchers is limited to two dimensions in the valuation of multi-asset options. Some authors such as Yuwei Chen [3] gave their formulation in terms of Black Scholes Partial Differential Equation (PDE) and considered numerical method for obtaining the prices. The authors, Carol Alexander et al., (2009) [4] did not relent in their effort as they presented an analytic approximation for Multi-asset Options Pricing but their approach was different from the one we gave here. In recent time, an existence result of solutions for a multi-dimensional stochastic control problem with singular state constraint was presented by Ulrich Horst and Xiaonyu Xia, (2018) [5]. The problem at hand is not centered on the specialty of the type of multi-asset but how to handle the nature of multi-assets amidst other conditional forces of uncertainty and dimensional challenges in the valuation process. According to Yuwei Chen [3] , most multi-asset European options and all American options have no analytical formula giving their prices, therefore, numerical methods are employed to approximate such prices.

We consider challenges of uncertainty posed by instability of economic factors on the payoff of assets. The keen economic factor to us is recession. We consider volatility variation imposed on options prices during economic recession which we termed economic recession induced volatility in addition to other volatility uncertainties of options price from other sources. Fast Fourier Transform algorithm is used in our formulation. Many authors have worked on Fourier transform of some options valuation such as ([6] [7] [8] [9]) among others. We gave a framework for extending Carr & Madan [6] Fast Fourier Transform approach of valuating an option on a single underlying asset to valuation of multi-assets options. Our major contribution is seen in valuation of multi-assets option in both finite and infinite dimensions and incorporation of economic recession factor on the volatility of assets during the state of economic recession.

The rest part of this paper is organized as follows. In Section 2, we gave preliminaries on Fast Fourier Transform. Section 3 is the Main result, which consists of subsections Fast Fourier Transform of multi-assets in finite dimension and Fast Fourier Transform of multi-assets in infinite dimension. Section 4 is the application on three assets in 3-dimensional case while Section 5 shows Numerical results on multi-assets in 3-dimensions. The last section is the conclusion part.

2. Preliminaries

2.1. Some Definitions on Fourier Transform

Definition 1: Let $f:R\to R$ be a real-value function for $x\in R$, then the Fourier transform of f is defined as

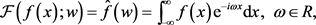(1)

where $i=\sqrt{-1}$ and $\omega$ is a parameter. We can recover $f\left(x\right)$ from $f\left(\omega \right)$ by the inverse Fourier transform.

Definition 2: The inverse Fourier transform of the real valued function $f\left(x\right)$ is defined by

${\mathcal{F}}^{-1}\left(\hat{f}\left(\omega \right);x\right)=f\left(x\right)=\frac{1}{2\text{π}}{\displaystyle {\int }_{-\infty }^{\infty }\hat{f}\left(w\right){\text{e}}^{i\omega x}\text{d}\omega },x\in R$ (2)

which belongs to L²-spaces.

Some certain axioms on Fourier transform exist in literature. Among such axioms are: convolution axiom, Translation axiom, Linearity axiom, Differentiation axiom, Symmetric axiom etc.

2.2. Some Axioms of Fourier Transform

· Convolution axiom: This property is considered very crucial as convolution of functions is mapped into multiplication in Fourier space.

Let $f,g\in L^2$ -space.

Then their convolution is defined by

$\left(f\star g\right)\left(x\right)={\displaystyle {\int }_{-\infty }^{\infty }f\left(x-y\right)g\left(y\right)\text{d}y}={\displaystyle {\int }_{-\infty }^{\infty }f\left(y\right)g\left(x-y\right)\text{d}y}$ (3)

The Fourier transform of the convolution of the functions f and g with convolution operator $\star$ is given by

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }\left[f\left(x-y\right)g\left(y\right)\text{d}y\right]{\text{e}}^{-i\omega x}\text{d}x}=\hat{f}\left(\omega \right)\hat{g}\left(\omega \right)$ (4)

The proof of Equation (4) is given in what follows.

Proof:

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }\left[{\displaystyle {\int }_{-\infty }^{\infty }f\left(x-y\right)g\left(y\right)\text{d}y}\right]{\text{e}}^{-i\omega x}\text{d}x}$ (5)

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }\left[{\displaystyle {\int }_{-\infty }^{\infty }f\left(x-y\right)g\left(y\right){\text{e}}^{-i\omega x}\text{d}y}\right]\text{d}x}$ (6)

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }\left[{\displaystyle {\int }_{-\infty }^{\infty }f\left(x-y\right)g\left(y\right){\text{e}}^{-i\omega x}\text{d}x}\right]\text{d}y}$ (7)

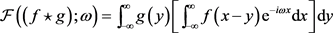(8)

To this end, one will have

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }g\left(y\right){\text{e}}^{-i\omega y}\left[{\displaystyle {\int }_{-\infty }^{\infty }f\left(\zeta \right){\text{e}}^{-i\omega \left(\zeta +y\right)}\text{d}\zeta }\right]\text{d}y}$ (9)

$\mathcal{F}\left(\left(f\star g\right);\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }g\left(y\right){\text{e}}^{-i\omega \left(y\right)}\left[{\displaystyle {\int }_{-\infty }^{\infty }f\left(\zeta \right){\text{e}}^{-i\omega \zeta }\text{d}\zeta }\right]\text{d}y}$ (10)

$\mathcal{F}\left(\left(f\star g\right);\omega \right)=\hat{f}\left(\omega \right){\displaystyle {\int }_{-\infty }^{\infty }g\left(y\right){\text{e}}^{-i\omega y}\text{d}y}$ (11)

$\mathcal{F}\left(\left(f\star g\right);\omega \right)=\hat{f}\left(\omega \right)\hat{g}\left(\omega \right).$ (12)

Similarly,

$\mathcal{F}\left(fg;\omega \right)=\mathcal{F}\left(f\left(x;\omega \right)\right)\star \mathcal{F}\left(g\left(x;\omega \right)\right)$ (13)

$\mathcal{F}\left(fg;\omega \right)={\displaystyle {\int }_{-\infty }^{\infty }f\left(x\right){\text{e}}^{-i\omega x}\text{d}x}\star {\displaystyle {\int }_{-\infty }^{\infty }g\left(x\right){\text{e}}^{-i\omega x}\text{d}x}$ (14)

$\mathcal{F}\left(fg;\omega \right)=\hat{f}\left(\omega \right)\star \hat{g}\left(\omega \right).$ (15)

The notion of Fourier transform is related to characteristic function in the following sense.

Definition 3: Suppose $P\left(x\right)$ is a probability distribution function with $x\in R$ . Then a characteristic function $\varphi \left(\omega \right),\omega \in IR$ is defined as the Fourier transform of $P\left(x\right)$ by

$\mathcal{F}\left(P\left(x\right);\omega \right)\equiv \hat{\varphi }\left(\omega \right)\equiv {\displaystyle {\int }_{-\infty }^{\infty }P\left(x\right){\text{e}}^{i\omega x}\text{d}\omega }=\mathbb{E}\left[{\text{e}}^{i\omega x}\right]$ (16)

One can recover the probability distribution function $P\left(x\right)$ by taking the inverse Fourier transform of the characteristics function just as the definition of inverse Fourier transform presented in Equation (2).

This is given by

$P\left(x\right)={\mathcal{F}}^{-1}\left(\hat{\varphi }\left(\omega \right)\right)=\frac{1}{2\text{π}}{\displaystyle {\int }_{-\infty }^{\infty }\hat{\varphi }\left(\omega \right){\text{e}}^{-i\omega x}\text{d}\omega }$ (17)

The reader can see the reference ([10]) and other standard texts on Fourier transform for more information.

There are available models for predicting economic recession probabilities especially on US recession (See [11]). The application of probability theory is found useful in such estimation [12]. Philip et al. [13] gave an intuition in predicting price dynamics in the presence of economic recession via recurrence relation technique and further presented a simple model showing the future of an economy under the exposure of recession if strong strategies and policies were not put in place to revive the economy. Fabio, Fornari and Antonio, Mele in (2009) [14] showed some connections between Financial Volatility and Economic Activity.

In sequel, we examine uncertainty on options value pose by recession on the volatility parameter of an option.

Assumption: Supposed that there are two sources of volatility variation on the assets. These are classified into economic recession induced volatility, $v^{rec}$, and the usual volatility from other sources, $v^{*}$, all assumed to be stochastic in nature. The volatility of the options is then given by

$V\left(t\right)=\{\begin{array}{ll}{v}^{rec}+v^{*},\hfill & \text{iftheeconomyisinrecession};\hfill \\ v^{*},\hfill & \text{ifeconomyisrecessionfree}.\hfill \end{array}$ (18)

where $v^{rec}$ is economy recession induced volatility in the stock market which arises due to information flow from the recessed Economy while $v^{*}$ is the volatility in the market from other sources. The study of parameters uncertainties in some financial models has received attention in the past few years. Two of those authors are [15] and [16]. Unfortunantely, many authors are yet to consider uncertaianties parameters that focus on economic recession in most Financial models use especially in derivative pricing. This present research is believed to stand out in that regards as it is hoped that more attention of authors will be drawn to economic recession and its effects in options pricing.

3. The Main Result

1) The Fast Fourier Transform (FFT) algorithm goes thus.

2) First get the characteristic function of the distribution. 2. Derive an analytic expression for the Fourier Transform of the modified options price wrt the characteristic function.

3) Find the Fourier inversion of the pricing function.

4) Perform Discrete Fourier transform in both step 2 and 3 above and apply Trapezoidal rule.

5) Choose uniform grid size for the computation of the FFT in step 4.

6) Make choices on the values assumed by other parameters such as N, the decay rate ( $\alpha$ ), etc. for optimality purpose.

3.1. Fast Fourier Transform of Multi-Assets in Finite Dimension

Consider an n-factor underlying asset $S_j,j=1,2,\cdots ,n$ . The payoff function $H\left(S,K\right)$ of the options at maturity time on the given underlying multi-assets is defined as

$H\left(S,K\right)=\underset{j=1}{\overset{n}{{\displaystyle \prod }}}\left(c{\left(S_j-K_j\right)}^{+}\right).$ (19)

$H\left(S,K\right)=\left(c{\left(S_1-K_1\right)}^{+}\cdot c{\left(S_2-K_2\right)}^{+}\cdot c{\left(S_3-K_3\right)}^{+}\cdots c{\left(S_n-K_n\right)}^{+}\right)$ (20)

where the $S_j$ and $K_j$ are respectively asset and strike prices.

The

${\left(S_j-K_j\right)}^{+}=\left(\text{max}\left(S_j-K_j,0\right),\text{foreach}j=1,2,\cdots ,n\right)$

The parameter c is a control switch between call or put options. If c as defined in the Equations (19) and (20) is −1, then one has put option and if $c=+1$, one has call option.

Let $k_j,s_j|j=1,2,\cdots ,n$ be logarithm of the strikes $K_j$ and assets $S_j$ prices respectively. Then, the option values computation in n-dimension is given by

$\begin{array}{l}{V}_T\left(k_1,k_2,\cdots ,k_n\right)\\ =E^{\mathcal{Q}}\left({\text{e}}^{-rT}{\left(S_1\left(T\right)-K_1\left(T\right)\right)}^{+}\cdot {\left(S_2\left(T\right)-K_2\left(T\right)\right)}^{+}\cdots {\left(S_n\left(T\right)-K_n\left(T\right)\right)}^{+}\right)\end{array}$ (21)

where $\mathcal{Q}$ is taken to be risk neutral measure while $q_T$ is the joint density function of each $s_j\left(T\right),j=1,2,\cdots ,n$ .

The integral representation of Equation (21) is given as

$\begin{array}{l}{V}_T\left(k_1,k_2,\cdots ,k_n\right)\\ ={\displaystyle {\int }_{k_1}^{\infty }{\displaystyle {\int }_{k_2}^{\infty }\cdots }}{\displaystyle {\int }_{k_n}^{\infty }{\text{e}}^{-rT}\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\cdots \left({\text{e}}^{s_n}-{\text{e}}^{k_n}\right)}\\ \times q_T\left(s_1,s_2,\cdots ,s_n\right)\text{d}{s}_n\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (22)

We gave the characteristic function corresponding to the joint density as

$\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\phi \left(u_1,u_2,\cdots ,u_n\right)=E^{\mathcal{Q}}\left({\text{e}}^{{\displaystyle \sum i{u}_j{s}_j\left(T\right)}}\right)$ (23)

$\phi \left(u_1,u_2,\cdots ,u_n\right)={\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{i{u}_1{s}_1+i{u}_2{s}_2+\cdots +i{u}_n{s}_n}{q}_T\left(s_1,s_2,\cdots ,s_n\right)\text{d}{s}_n\cdots \text{d}{s}_2\text{d}{s}_1}.$ (24)

In order to ensure the square integrability of the right hand side of the Equation (22), we take its product and a decaying term $\alpha$ over $k_j$ .

This we expressed as

$c_T\left(k_1{k}_2,\cdots ,k_n\right)={\text{e}}^{{\alpha }_1{k}_1+{\alpha }_2{k}_2+\cdots +{\alpha }_n{k}_n}\times V_T\left(k_1,k_2,\cdots ,k_n\right),{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n>0.$ (25)

For the call option, the Fourier transform of the modified option prices is given by

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_n\right)\\ ={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }\cdots }}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{i\left(u_1{k}_1+u_2{k}_2+\cdots +u_n{k}_n\right)}{c}_T\left(k_1,k_2,\cdots ,k_n\right)\text{d}{k}_n\cdots \text{d}{k}_2\text{d}{k}_1}\end{array}$ (26)

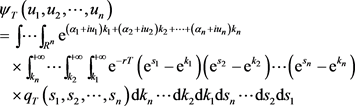(27)

This is further simplified as follows

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_n\right)\\ ={\displaystyle \int \cdots }{\displaystyle {\int }_{\text{}\text{}{R}^n}{\text{e}}^{-rT}{q}_T\left(s_1,s_2,\cdots ,s_n\right)}\\ \times {\displaystyle {\int }_{\infty }^{s^n}\cdots }{\displaystyle {\int }_{\infty }^{s^2}{\displaystyle {\int }_{\infty }^{s^1}{\text{e}}^{-rT}\left(\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\cdots \left({\text{e}}^{s_n}-{\text{e}}^{k_n}\right)\right)}}\\ \times {\text{e}}^{\left({\alpha }_1+i{u}_1\right)k_1+\left({\alpha }_2+i{u}_2\right)k_2+\cdots +\left({\alpha }_n+i{u}_n\right)k_n}\text{d}{k}_n\cdots \text{d}{k}_2\text{d}{k}_1\text{d}{s}_n\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (28)

which reduces to

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_n\right)\\ ={\displaystyle \int \cdots }{\displaystyle {\int }_{\text{}\text{}{R}^n}{\text{e}}^{-rT}{q}_T\left(s_1,s_2,\cdots ,s_n\right)}\\ \times \left(\frac{\left({\text{e}}^{\left(1+{\alpha }_1+i{u}_1\right)s_1+\left(1+{\alpha }_2+i{u}_2\right)s_2+\cdots +\left(1+{\alpha }_n+i{u}_n\right)s_n}\right)}{\left({\alpha }_1+i{u}_1\right)\left(1+{\alpha }_1+i{u}_1\right)\left({\alpha }_2+i{u}_2\right)\left(1+{\alpha }_2+i{u}_2\right)\cdots \left({\alpha }_n+i{u}_n\right)\left(1+{\alpha }_n+i{u}_n\right)}\right)\text{d}{s}_n\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (29)

For a known characteristic function or a calculated affine characteristic function ${\phi }_T$ of a given process, it is possible to derive an analytic close form formula for ${\Psi }_T\left(u_1,u_2,\cdots ,u_n\right)$ which is the Fourier transform of the multi-assets.

Applying definition (2), we expressed the Fourier transform of (21) through (28)-(29) as

$\begin{array}{l}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}{V}_T\left(k_1,k_2,\cdots ,k_n\right)\\ =\frac{{\text{e}}^{-\left({\alpha }_1{k}_1+{\alpha }_2{k}_2+\cdots +{\alpha }_n{k}_n\right)}}{{\left(2\text{π}\right)}^n}\underset{n\text{-tuple}}{\underset{︸}{{\displaystyle {\int }_{-\infty }^{\infty }\cdots }{\displaystyle {\int }_{-\infty }^{\infty }}}}{\text{e}}^{-i\left(u_1{k}_1+u_2{k}_2+\cdots +u_n{k}_n\right)}{\psi }_T\left(u_1,u_2,\cdots ,u_n\right)\text{d}{u}_k\cdots \text{d}{u}_2\text{d}{u}_1.\end{array}$ (30)

Rewriting the integrals in series form using trapezoidal rule, equation (30) is transformed to

(31)

where

, while $h_j,j=1,2,\cdots ,n$ denote integration steps here

For a single asset, Fast Fourier Transform (FFT) equation is defined in the form of

$H\left(k\right)=\underset{j=1}{\overset{N-1}{{\displaystyle \sum }}}{\text{e}}^{-i\frac{2\text{π}}{N}\left(j-1\right)\left(k-1\right)}{y}_j,1\le k\le N.$ (32)

Therefore, in the light of Equation (32), we gave an n-dimension version of $y_j,j=1,2,\cdots ,n$, such that in an effort to capture the imaginary part of the complex form of $y_j$, which is inclusive in Fourier transform, we have

${\xi }_j|j=1,2,\cdots ,n:=\underset{m_1=1}{\overset{N_1-1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_1-1}{{\displaystyle \sum }}}\cdots \underset{m_n=1}{\overset{N_1-1}{{\displaystyle \sum }}}{\text{e}}^{-i\left(\frac{2\text{π}}{N_1}{j}_1{m}_1+\frac{2\text{π}}{N_2}{j}_2{m}_2+\cdots +\frac{2\text{π}}{N_n}{j}_n{m}_n\right)}{y}_j,j=1,2,\cdots ,n$ (33)

where $m_1=1,2,\cdots ,N_1-1;m_2=1,2,\cdots ,N_2-1$ respectively.

The integration steps $h_j,j=1,2,\cdots ,n$, in (31) is uniformly chosen such that

$h_1=\frac{u_{1,m_1}}{\left(m_1-\frac{N}{2}\right)},h_2=\frac{u_{2,m_2}}{\left(m_2-\frac{N}{2}\right)},\cdots ,h_n=\frac{u_{n,m_n}}{\left(m_n-\frac{N}{2}\right)}$

Considering a uniform grid size of $N\times N$ array and set.

The size of the uniform spacing $\zeta$ between the N values of vector k with respect to the integration steps $h_j,j=1,2,\cdots ,n$ and Equation (33) has the following relation

${\zeta }_1{h}_1={\zeta }_2{h}_2=\cdots ={\zeta }_n{h}_n=\frac{\text{2π}}{N}$ (34)

The options prices $V_T$ over log strikes from Equation (31) is now given as

$\begin{array}{l}{V}_T\left(k_{1,p_1},k_{2,p_2},\cdots ,k_{n,p_n}\right)\\ \approx \frac{{\text{e}}^{-\left({\alpha }_1{k}_{1,p_1}+{\alpha }_2{k}_{2,p_2}+\cdots +{\alpha }_n{k}_{n,p_n}\right)}}{{\left(2\text{π}\right)}^n}\Omega \left(k_{1,p_1},k_{2,p_2},\cdots ,k_{n,p_n}\right)\underset{j=1}{\overset{n}{{\displaystyle \prod }}}{h}_j,\\ \text{for}0\le p_1,p_2,\cdots ,p_n\le N-1.\end{array}$ (35)

where

$\begin{array}{l}\Omega \left(k_{1,p_1},k_{2,p_2},\cdots ,k_{n,p_n}\right)\\ =\underset{m_1=1}{\overset{N_1-1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_1-1}{{\displaystyle \sum }}}\cdots \underset{m_n=1}{\overset{N_1-1}{{\displaystyle \sum }}}{\text{e}}^{-\frac{\text{2π}}{N}\left(\left(m_1-\frac{N}{2}\right)\left(p_1-\frac{N}{2}\right)+\left(m_2-\frac{N}{2}\right)\left(p_2-\frac{N}{2}\right)+\cdots +\left(m_n-\frac{N}{2}\right)\left(p_n-\frac{N}{2}\right)\right)}{\psi }_T\left(u_1,u_2,\cdots ,u_n\right)\end{array}$

Remarks:

1) The Equation (35) above is fast Fourier transform formula which can be adopted to calculate the value of European call option prices on finite -dimensional underlying multi-assets.

2) The corresponding European put option value can be obtained if we set the control parameter $c=-1$ in the Equations (19)-(20) such that the sign attached to the log strikes and log assets changes in Equation (21) follow the same procedure through to arrive at (35). Alternatively, the put values can be obtained via put-call parity.

3.2. Fast Fourier Transform of Multi-Assets in an Infinite Dimension

Following similar algorithm presented in finite dimensional case, the above formulation can be extended to an infinite dimension as follows.

The payoff function $H\left(S,K\right)$ of the options at maturity time on the given underlying multi-assets in an infinite dimension is given as

$H\left(S,K\right)=\underset{j=1}{\overset{\infty }{{\displaystyle \prod }}}\left(c\left(S_j-K_j\right)\right)$ (36)

$\begin{array}{l}H\left(S,K\right)\\ =\left(c{\left(S_1-K_1\right)}^{+}\cdot c{\left(S_2-K_2\right)}^{+}\cdot c{\left(S_3-K_3\right)}^{+}\cdots c{\left(S_n-K_n\right)}^{+}\cdot c{\left(S_{n+1}-K_{n+1}\right)}^{+}\cdots \right)\end{array}$ (37)

where the $S_j$ and $K_j$ are respectively asset and strike prices. The parameter c is a control in switching between call or put options as discussed earlier.

Let $k_j,s_j|j=1,2,\cdots ,n,n+1,\cdots$ be logarithm of the strikes $K_j$ and assets $S_j$ prices respectively. Then, the option values computation in infinite-dimension is given by

$\begin{array}{l}{V}_T\left(k_1,k_2,\cdots ,k_{n+1},\cdots \right)\\ =E^{\mathcal{Q}}\left({\text{e}}^{-rT}{\left(S_{1_T}-K_{1_T}\right)}^{+}\cdot {\left(S_{2_T}-K_{2_T}\right)}^{+}\cdots {\left(S_{n_T}-K_{n_T}\right)}^{+}\cdot {\left(S_{n+1_T}-K_{n+1_T}\right)}^{+}\cdots \right)\end{array}$ (38)

where $\mathcal{Q}$ still remain as risk neutral measure and $q_T$ is the joint density function for each

$s_j\left(T\right),j=1,2,\cdots ,n,n+1,\cdots$

The characteristic function corresponding to the joint density is given as

$\begin{array}{l}\phi \left(u_1,u_2,\cdots ,u_{n+1},\cdots \right)\\ ={\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{i{u}_1{s}_1+i{u}_2{s}_2+\cdots +i{u}_{n+1}{s}_{n+1}+\cdots }{q}_T\left(s_1,s_2,\cdots ,s_{n+1},\cdots \right)\text{d}{s}_{n+1}\cdots \text{d}{s}_2\text{d}{s}_1}.\end{array}$

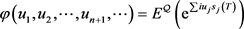
The Fourier transform of the modified call option prices is given by

$\begin{array}{l}\phi \left(u_1,u_2,\cdots ,u_{n+1},\cdots \right)\\ ={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }\cdots }}{\displaystyle {\int }_{-\infty }^{\infty }}{\text{e}}^{i\left(u_1{k}_1+u_2{k}_2+\cdots +u_{n+1}{k}_{n+1}+\cdots \right)}{c}_T\left(k_1,k_2,\cdots ,k_{n+1},\cdots \right)\text{d}{k}_{n+1}\cdots \text{d}{k}_2\text{d}{k}_1\end{array}$ (39)

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_{n+1},\cdots \right)\\ ={\displaystyle \int \cdots }{\displaystyle {\int }_{I{R}^n}{\text{e}}^{\left({\alpha }_1+i{u}_1\right)k_1+\left({\alpha }_2+i{u}_2\right)k_2+\cdots +\left({\alpha }_{n+1}+i{u}_{n+1}\right)k_{n+1}+\cdots }}\\ \times {\displaystyle {\int }_{k_{n+1}}^{+\infty }\cdots }{\displaystyle {\int }_{k_2}^{+\infty }{\displaystyle {\int }_{k_1}^{+\infty }{\text{e}}^{-rT}\left(\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\cdots \left({\text{e}}^{s_{n+1}}-{\text{e}}^{k_{n+1}}\right)\cdots \right)}}\\ \times q_T\left(s_1,s_2,\cdots ,s_{n+1},\cdots \right)\text{d}{k}_{n+1}\cdots \text{d}{k}_2\text{d}{k}_1\text{d}{s}_{n+1}\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (40)

Further simplification yields

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_{n+1},\cdots \right)\\ ={\displaystyle \int \cdots }{\displaystyle \int {\text{e}}^{-rT}{q}_T\left(s_1,s_2,\cdots ,s_{n+1},\cdots \right)}\\ \times {\displaystyle {\int }_{\infty }^{s^2}{\displaystyle {\int }_{\infty }^{s^1}{\text{e}}^{-rT}\left(\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\cdots \left({\text{e}}^{s_{n+1}}-{\text{e}}^{k_{n+1}}\right)\cdots \right)}}\\ \times {\text{e}}^{\left({\alpha }_1+i{u}_1\right)k_1+\left({\alpha }_2+i{u}_2\right)k_2+\cdots +\left({\alpha }_{n+1}+i{u}_{n+1}\right)k_{n+1}+\cdots }\text{d}{k}_{n+1}\cdots \text{d}{k}_2\text{d}{k}_1\text{d}{s}_{n+1}\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (41)

which reduces to

$\begin{array}{l}{\psi }_T\left(u_1,u_2,\cdots ,u_{n+1},\cdots \right)\\ ={\displaystyle \int \cdots }{\displaystyle {\int }_{R^{\infty }}{\text{e}}^{-rT}{q}_T\left(s_1,s_2,\cdots ,s_{n+1},\cdots \right)}\\ \times \left(\frac{\left({\text{e}}^{\left(1+{\alpha }_1+i{u}_1\right)s_1+\left(1+{\alpha }_2+i{u}_2\right)s_2+\cdots +\left(1+{\alpha }_{n+1}+i{u}_{n+1}\right)s_{n+1}+\cdots }\right)}{\left({\alpha }_1+i{u}_1\right)\left(1+{\alpha }_1+i{u}_1\right)\left({\alpha }_2+i{u}_2\right)\left(1+{\alpha }_2+i{u}_2\right)\cdots \left({\alpha }_{n+1}+i{u}_{n+1}\right)\left(1+{\alpha }_{n+1}+i{u}_{n+1}\right)\cdots }\right)\cdots \text{d}{s}_{n+1}\cdots \text{d}{s}_2\text{d}{s}_1\end{array}$ (42)

Expressing the integrals in discrete Fourier transform and using trapezoidal rule, we have

$\begin{array}{l}{V}_T\left(k_1,k_2,\cdots ,k_{n+1},\cdots \right)=\frac{{\text{e}}^{-\left({\alpha }_1{k}_1+{\alpha }_2{k}_2+\cdots +{\alpha }_{n+1}{k}_{n+1}+\cdots \right)}}{{\left(\text{2π}\right)}^{n+\nu }}\\ \times \underset{m_1=1}{\overset{N_1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_2}{{\displaystyle \sum }}}\cdots \underset{m_{\infty }}{\overset{N_{\infty }}{{\displaystyle \sum }}}{\text{e}}^{-i\left(u_{1,m_1}{k}_1+u_{2,m_2}{k}_2+\cdots \right)}{\psi }_T\left(u_{1,m_1},u_{2,m_2},\cdots ,u_{n+1,m_{n+1}}\cdots \right)\underset{j=1}{\overset{\infty }{{\displaystyle \prod }}}{h}_j\end{array}$ (43)

where

$\underset{j=1}{\overset{\infty }{{\displaystyle \prod }}}{h}_j=h_1{h}_2\cdots h_{n+1}\cdots$, while $h_j$, $j=1,2,\cdots ,n+1,\cdots$ denote integration steps here and $\nu$ is a very large integer.

The options prices $V_T$ over log strikes $k=\log K$ are finally given as

$\begin{array}{l}{V}_T\left(k_{1,p_1},k_{2,p_2}\cdots ,k_{n+1,p_{n+1}},\cdots \right)\\ \approx \frac{{\text{e}}^{-\left({\alpha }_1{k}_{1,p_1}+{\alpha }_2{k}_{2,p_2}+\cdots +{\alpha }_{n+1}{k}_{n+1,p_{n+1}}+\cdots \right)}}{{\left(\text{2π}\right)}^{n+\nu }}\Omega \left(k_{1,p_1},k_{2,p_2},\cdots ,k_{n,p_n}\right)\underset{j=1}{\overset{\infty }{{\displaystyle \prod }}}{h}_j\end{array}$ (44)

where $0\le p_1,p_2,\cdots ,p_{n+1},\cdots \le N-1$ and

$\begin{array}{l}\Omega \left(k_{1,p_1},k_{2,p_2},\cdots ,k_{n+1,p_{n+1}},\cdots \right)\\ =\underset{m_1=1}{\overset{N_1-1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_1-1}{{\displaystyle \sum }}}\cdots \underset{m_{n+1}=1}{\overset{N_1-1}{{\displaystyle \sum }}}\cdots {\text{e}}^{-\frac{\text{2π}}{N}\left(\left(m_1-\frac{N}{2}\right)\left(p_1-\frac{N}{2}\right)+\left(m_2-\frac{N}{2}\right)\left(p_2-\frac{N}{2}\right)+\cdots +\left(m_{n+1}-\frac{N}{2}\right)\left(p_{n+1}-\frac{N}{2}\right)\right)}\\ \times {\psi }_T\left(u_1,u_2,\cdots ,u_{n+1}\cdots \right)\end{array}$

We acknowledge Carr & Madan (1999) [6] for providing a fast Fourier Transform framework on single underlying asset which we extended to multi-assets in both finite dimension and infinite dimension in this paper.

4. Application on Three Assets in 3-Dimensional Case

Let $S_j|j=1,2,3$ be three underlying assets and strike prices $K_j|j=1,2,3$ respectively. The payoff function is defined in the light of Equation (20) as

$H\left(S,K\right)=\left(c{\left(S_1-K_1\right)}^{+}\cdot c{\left(S_2-K_2\right)}^{+}\cdot c{\left(S_3-K_3\right)}^{+}\right)$, $c=+1$ for call option. (45)

where the $S_j$ and $K_j$ are respectively asset and strike prices.

The option values computation in 3-dimension is given by

$\begin{array}{l}{V}_T\left(k_1,k_2,k_3\right)\\ =E^{\mathcal{Q}}\left({\text{e}}^{-rT}{\left(S_1\left(T\right)-K_1\left(T\right)\right)}^{+}\cdot {\left(S_2\left(T\right)-K_2\left(T\right)\right)}^{+}\cdot {\left(S_3\left(T\right)-K_3\left(T\right)\right)}^{+}\right)\end{array}$ (46)

where $\mathcal{Q}$ is a risk neutral measure and $q_T$ is the joint density function of each $s_j\left(T\right),j=1,2,3$ .

The integral representation of Equation (46) is given as

$\begin{array}{l}{V}_T\left(k_1,k_2,k_3\right)\\ ={\displaystyle {\int }_{k_1}^{\infty }{\displaystyle {\int }_{k_2}^{\infty }{\displaystyle {\int }_{k_3}^{\infty }{\text{e}}^{-rT}\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\left({\text{e}}^{s_3}-{\text{e}}^{k_3}\right)q_T\left(s_1,s_2,s_3\right)\text{d}{s}_3\text{d}{s}_2\text{d}{s}_1}}}.\end{array}$ (47)

The characteristic function corresponding to the joint density is given by

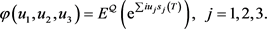(48)

$\phi \left(u_1,u_2,u_3\right)={\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{i{u}_1{s}_1+i{u}_2{s}_2+i{u}_3{s}_3}{q}_T\left(s_1,s_2,s_3\right)\text{d}{s}_3\text{d}{s}_2\text{d}{s}_1}.$ (49)

Multiplying the right side of Equation (47) and decaying term say $\alpha$ over $k_1,k_2,k_3$ so as to have square integrable of the right side of (47).

We expressed the result as

$c_T\left(k_1,k_2,k_3\right)={\text{e}}^{{\alpha }_1{k}_1+{\alpha }_2{k}_2+{\alpha }_3{k}_3}\times V_T\left(k_1,k_2,k_3\right),{\alpha }_1,{\alpha }_2,{\alpha }_3>0.$ (50)

For the call option, the Fourier transform of the modified option prices is given by

${\psi }_T\left(u_1,u_2,u_3\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{i\left(u_1{k}_1+u_2{k}_2+u_3{k}_3\right)}{c}_T\left(k_1,k_2,k_3\right)\text{d}{k}_3\text{d}{k}_2\text{d}{k}_1}}}$ (51)

$\begin{array}{c}{\psi }_T\left(u_1,u_2,u_3\right)={\displaystyle {\int }_{I{R}^3}{\text{e}}^{\left({\alpha }_1+i{u}_1\right)k_1+\left({\alpha }_2+i{u}_2\right)k_2+\left({\alpha }_3+i{u}_3\right)k_3}}\\ \times {\displaystyle {\int }_{k_3}^{+\infty }{\displaystyle {\int }_{k_2}^{+\infty }{\displaystyle {\int }_{k_1}^{+\infty }{\text{e}}^{-rT}\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\left({\text{e}}^{s_3}-{\text{e}}^{k_3}\right)}}}\\ \times q_T\left(s_1,s_2,s_3\right)\text{d}{k}_3\text{d}{k}_2\text{d}{k}_1\text{d}{s}_3\text{d}{s}_2\text{d}{s}_1\end{array}$ (52)

Further simplification yields

$\begin{array}{c}{\psi }_T\left(u_1,u_2,u_3\right)={\displaystyle {\int }_{I{R}^3}{\text{e}}^{-rT}{q}_T\left(s_1,s_2,s_3\right)}\\ \times {\displaystyle {\int }_{\infty }^{s^3}{\displaystyle {\int }_{\infty }^{s^2}{\displaystyle {\int }_{\infty }^{s^1}{\text{e}}^{-rT}\left(\left({\text{e}}^{s_1}-{\text{e}}^{k_1}\right)\left({\text{e}}^{s_2}-{\text{e}}^{k_2}\right)\left({\text{e}}^{s_3}-{\text{e}}^{k_3}\right)\right)}}}\\ \times {\text{e}}^{\left({\alpha }_1+i{u}_1\right)k_1+\left({\alpha }_2+i{u}_2\right)k_2+\left({\alpha }_3+i{u}_3\right)k_3}\text{d}{k}_3\text{d}{k}_2\text{d}{k}_1\text{d}{s}_3\text{d}{s}_2\text{d}{s}_1\end{array}$ (53)

which reduces to

$\begin{array}{l}{\psi }_T\left(u_1,u_2,u_3\right)={\displaystyle {\int }_{I{R}^3}{\text{e}}^{-rT}{q}_T\left(s_1,s_2,s_3\right)}\\ \times \left[\frac{\left({\text{e}}^{\left(1+{\alpha }_1+i{u}_1\right)s_1+\left(1+{\alpha }_2+i{u}_2\right)s_2+\left(1+{\alpha }_3+i{u}_3\right)s_3}\right)}{\left({\alpha }_1+i{u}_1\right)\left(1+{\alpha }_1+i{u}_1\right)\left({\alpha }_2+i{u}_2\right)\left(1+{\alpha }_2+i{u}_2\right)\left({\alpha }_3+i{u}_3\right)\left(1+{\alpha }_3+i{u}_3\right)}\right]\text{d}{s}_3\text{d}{s}_2\text{d}{s}_1\end{array}$ (54)

Consider a known characteristic function ${\phi }_T$ for the distributions, an analytical close form formula for ${\Psi }_T\left(u_1,u_2,u_3\right)$ which is the Fourier transform of the 3-dimensional multi-assets is given by

$\begin{array}{l}{V}_T\left(k_1,k_2,k_3\right)\\ =\frac{{\text{e}}^{-\left({\alpha }_1{k}_1+{\alpha }_2{k}_2+{\alpha }_3{k}_3\right)}}{{\left(\text{2π}\right)}^3}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-i\left(u_1{k}_1+u_2{k}_2+u_3{k}_3\right)}{\psi }_T\left(u_1,u_2,u_3\right)\text{d}{u}_3\text{d}{u}_2\text{d}{u}_1}}}.\end{array}$ (55)

Rewriting the integrals in series form using trapezoidal rule, equation (55) is transformed to

$\begin{array}{l}{V}_T\left(k_1,k_2,k_3\right)\\ =\frac{{\text{e}}^{-\left({\alpha }_1{k}_1+{\alpha }_2{k}_2+{\alpha }_3{k}_3\right)}}{{\left(2\text{π}\right)}^3}\underset{\Omega \left(k_1,k_2,k_3\right)}{\underset{︸}{\underset{m_1=1}{\overset{N_1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_2}{{\displaystyle \sum }}}\underset{m_3=1}{\overset{N_3}{{\displaystyle \sum }}}{\text{e}}^{-i\left(u_{1,m_1}{k}_1+u_{2,m_2}{k}_2\right)}{\psi }_T\left(u_{1,m_1},u_{2,m_2},u_{3,m_3}\right)}}{h}_3{h}_2{h}_1\end{array}$ (56)

where $h_1{h}_2{h}_3$, is the product of the integration steps.

The general form of Fast Fourier Transform (FFT) equation for a single asset has been given in the form

$H\left(k\right)=\underset{j=1}{\overset{N-1}{{\displaystyle \sum }}}{\text{e}}^{-i\frac{2\text{π}}{N}\left(j-1\right)\left(k-1\right)}{y}_j,1\le k\le N.$ (57)

Whence, 3-dimensional version of $y_j,j=1,2,3$, in (57) so as to capture the imaginary part of the complex form of $y_j$, we have

${\xi }_j|j=1,2,3:=\underset{m_1=1}{\overset{N_1-1}{{\displaystyle \sum }}}\underset{m_2=1}{\overset{N_1-1}{{\displaystyle \sum }}}\underset{m_3=1}{\overset{N_1-1}{{\displaystyle \sum }}}{\text{e}}^{-i\left(\frac{\text{2π}}{N_1}{j}_1{m}_1+\frac{\text{2π}}{N_2}{j}_2{m}_2+\frac{\text{2π}}{N_3}{j}_3{m}_3\right)}{y}_j,j=1,2,3.$ (58)

where $m_1=1,2,\cdots ,N_1-1;m_2=1,2,\cdots ,N_2-1;m_3=1,2,\cdots ,N_2-1$, respectively.

The integration steps $h_j,j=1,2,3$, in (56) is uniformly chosen such that

$h_1=\frac{u_{1,m_1}}{\left(m_1-\frac{N}{2}\right)},h_2=\frac{u_{2,m_2}}{\left(m_2-\frac{N}{2}\right)},h_3=\frac{u_{3,m_3}}{\left(m_3-\frac{N}{2}\right)}$

Considering a uniform grid size of $N\times N$ array and set.

The size of the uniform spacing $\zeta$ between the N values of vector k with respect to the integration steps $h_j,j=1,2,3$ and Equation (58) has the following relation

${\zeta }_1{h}_1={\zeta }_2{h}_2={\zeta }_3{h}_3=\frac{\text{2π}}{N}$ (59)

The options prices $V_T$ over log strikes from Equation (56) is given by

$\begin{array}{l}{V}_T\left(k_{1,p_1},k_{2,p_2},k_{3,p_3}\right)\\ \approx \frac{{\text{e}}^{-\left({\alpha }_1{k}_{1,p_1}+{\alpha }_2{k}_{2,p_2}+{\alpha }_3{k}_{3,p_3}\right)}}{{\left(\text{2π}\right)}^3}\Omega \left(k_{1,p_1},k_{2,p_2},k_{3,p_3}\right)h_1{h}_2{h}_3,\\ \text{for}0\le p_1,p_2,p_3\le N-1.\end{array}$ (60)