Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T17:13:29.169Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure Discrete Spectrum for One-dimensional Substitution Systems of Pisot Type

Published online by Cambridge University Press:  20 November 2018

V. F. Sirvent  and
B. Solomyak
V. F. Sirvent
Affiliation:
Departamento de Matemáticas Universidad Simón Bolívar Apartado 89000 Caracas 1086-A Venezuela, e-mail: vsirvent@usb.ve
B. Solomyak
Affiliation:
Box 354350 Department of Mathematics University of Washington Seattle, Washington 98195 U.S.A., e-mail: solomyak@math.washington.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider two dynamical systems associated with a substitution of Pisot type: the usual $\mathbb{Z}$-action on a sequence space, and the 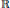$\mathbb{R}$-action, which can be defined as a tiling dynamical system or as a suspension flow. We describe procedures for checking when these systems have pure discrete spectrum (the “balanced pairs algorithm” and the “overlap algorithm”) and study the relation between them. In particular, we show that pure discrete spectrum for the 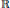$\mathbb{R}$-action implies pure discrete spectrum for the $\mathbb{Z}$-action, and obtain a partial result in the other direction. As a corollary, we prove pure discrete spectrum for every 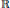$\mathbb{R}$-action associated with a two-symbol substitution of Pisot type (this is conjectured for an arbitrary number of symbols).

Keywords

37A3052C2337B10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 697 - 710
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Arnoux, P. and Ito, S., Pisot substitutions and Rauzy fractals. Bull. Belg. Math. Soc. Simon Stevin 8 (2001), 181–207.Google Scholar
[2] Barge, M. and Diamond, B., Coincidence for substitutions of Pisot type. 2001, preprint.Google Scholar
[3] Canterini, V. and Siegel, A., Geometric representation of substitutions of Pisot type. Trans. Amer. Math. Soc. 353 (2001), 5121–5144.Google Scholar
[4] Dekking, F. M., The spectrum of dynamical systems arising from substitutions of constant length. Z. Wahrsch. Verw. Gebiete 41 (1978), 221–239.Google Scholar
[5] Dworkin, S., Spectral theory and X-ray diffraction. J. Math. Phys. 34 (1993), 2965–2967.Google Scholar
[6] Ferenczi, S., Mauduit, C. and Nogueira, A., Substitution dynamical systems: algebraic characterization of eigenvalues. Ann. Sci. École Norm. Sup. 29 (1996), 519–533.Google Scholar
[7] Frougny, C. and Solomyak, B., Finite beta-expansions. Ergodic Theory Dynamical Systems 12 (1992), 713–723.Google Scholar
[8] Hof, A., Diffraction by aperiodic structures. In: The Mathematics of Long-Range Aperiodic Order, (ed. R. V. Moody), Kluwer, 1997, 239–268.Google Scholar
[9] Hollander, M., Linear numeration systems, finite β-expansions, and discrete spectrum for substitution dynamical systems. Ph.D. Thesis, University of Washington, 1996.Google Scholar
[10] Hollander, M. and Solomyak, B., Two-symbol Pisot substitutions have pure discrete spectrum. 2001, preprint.Google Scholar
[11] Host, B., Valeurs propres de systèmes dynamiques définis par de substitutions de longueur variable. Ergodic Theory Dynamical Systems 6 (1986), 529–540.Google Scholar
[12] Host, B., Représentation géométrique des substitutions sur 2 lettres. Unpublished manuscript, 1992.Google Scholar
[13] Lee, J.-Y., Moody, R. V. and Solomyak, B., Diffraction and Multi-dimensional Substitution Systems. 2001, preprint.Google Scholar
[14] Lind, D. and Marcus, B., Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
[15] Livshits, A. N., On the spectra of adic transformations of Markov compacta. Russian Math. Surveys 42 (1987), 222–223.Google Scholar
[16] Livshits, A. N., Some examples of adic transformations and substitutions. Selecta Math. Soviet. 11 (1992), 83–104.Google Scholar
[17] Michel, P., Coincidence values and spectra of substitutions. Z.Wahrsch. Verw. Gebiete 42 (1978), 205–227.Google Scholar
[18] Queffélec, M., Substitution Dynamical Systems.Spectral Analysis. Lecture Notes in Math. 1294, Springer-Verlag, Berlin, 1987.Google Scholar
[19] Radin, C., Space tilings and substitutions. Geom. Dedicata 55 (1995), 257–264.Google Scholar
[20] Radin, C. and Wolff, M., Space tilings and local isomorphism. Geom. Dedicata 42 (1992), 355–360.Google Scholar
[21] Rauzy, G., Nombres algébriques et substitutions. Bull. Soc. Math. France 110 (1982), 147–178.Google Scholar
[22] Siegel, A., Chapter 7: Spectral theory and geometric representation of substitutions. In: Substitutions in Dynamics, Arithmetics and Combinatorics, 199–252, (eds. V. Berthé, S. Ferenczi, C. Mauduit and A. Siegel), Lecture Notes in Math., Springer, to appear.Google Scholar
[23] Siegel, A., Répresentation des systèmes dynamiques substitutifs non unimodulaires. Ergodic Theory Dynamical Systems, to appear.Google Scholar
[24] Sirvent, V. F., Modelos geométricos asociados a substituciones. Trabajo de ascenso, Universidad Sim ón Bolívar, 1998.Google Scholar
[25] Sirvent, V. F. and Wang, Y., Self-affine tiling via substitution dynamical systems and Rauzy fractals. Pacific J. Math., to appear.Google Scholar
[26] Solomyak, B., On the spectral theory of adic transformations. Adv. Soviet Math. 9 (1992), 217–230.Google Scholar
[27] Solomyak, B., Dynamics of self-similar tilings. Ergodic Theory Dynamical Systems 17 (1997), 695–738. Corrections, ibid. 19(1999), 1685.Google Scholar
[28] Walters, P., An Introduction to Ergodic Theory. Springer Graduates Texts in Math., Springer-Verlag, New York, 1982.Google Scholar