Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T00:59:11.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonself-adjoint Semicrossed Products by Abelian Semigroups

Published online by Cambridge University Press:  20 November 2018

Adam Hanley Fuller
Adam Hanley Fuller*
Affiliation:
Department of Pure Mathematics, University of Waterloo, WaterlooON N2L 3G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 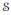$S$ be the semigroup 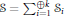$S=\sum\nolimits_{i=1}^{\oplus k}{{{S}_{i}}}$, where for each 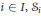$i\in I,{{S}_{i}}$ is a countable subsemigroup of the additive semigroup 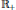${{\mathbb{R}}_{+}}$ containing 0. We consider representations of 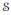$S$ as contractions 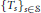${{\left\{ {{T}_{s}} \right\}}_{s\in S}}$ on a Hilbert space with the Nica-covariance property: 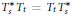$T_{s}^{*}{{T}_{t}}={{T}_{t}}T_{s}^{*}$ whenever 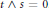$t\wedge s=0$. We show that all such representations have a unique minimal isometric Nica-covariant dilation.

This result is used to help analyse the nonself-adjoint semicrossed product algebras formed from Nica-covariant representations of the action of 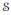$S$ on an operator algebra 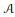$\mathcal{A}$ by completely contractive endomorphisms. We conclude by calculating the 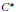${{C}^{*}}$-envelope of the isometric nonself-adjoint semicrossed product algebra (in the sense of Kakariadis and Katsoulis).

Keywords

47L5547A2047L65semicrossed productcrossed productC*-envelopedilations
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 768 - 782
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Arveson, W. B., Operator algebras and measure preserving automorphisms. Acta Math. 118(1967), 95–109. http://dx.doi.org/10.1007/BF02392478 Google Scholar
[2] Arveson, W. B., Subalgebras of C*-algebras. Acta Math. 123(1969), 141–224. http://dx.doi.org/10.1007/BF02392388 Google Scholar
[3] Arveson, W. B., Subalgebras of C*-algebras. II. Acta Math. 128(1972), 271–308. http://dx.doi.org/10.1007/BF02392166 Google Scholar
[4] Davidson, K. R. and Katsoulis, E. G., Semicrossed products of simple C*-algebras. Math. Ann. 342(2008), 515–525. http://dx.doi.org/10.1007/s00208-008-0244-1 Google Scholar
[5] Davidson, K. R., Dilating covariant representations of the non-commutative disc algebras. J. Funct. Anal. 259(2010), 817–831. http://dx.doi.org/10.1016/j.jfa.2010.04.005 Google Scholar
[6] Davidson, K. R., Biholomorphisms of the unit ball of Cn and semicrossed products. In: Operator theory live, Theta Ser. Adv. Math. 12, Theta, Bucharest, 2010, 69–80.Google Scholar
[7] Davidson, K. R., Semicrossed products of the disc algebra. Proc. Amer. Math. Soc., to appear. http://dx.doi.org/10.1090/S0002-9939-2012-11348-6Google Scholar
[8] Davidson, K. R., Dilation theory, commutant lifting and semicrossed products. Doc. Math. 16(2011), 781–868.Google Scholar
[9] Dritschel, M. and McCullough, S., Boundary representations of families of representations of operator algebras and spaces. J. Operator Theory 53(2005), 159–197.Google Scholar
[10] Duncan, B. L., C*-envelopes of universal free products and semicrossed products for multivariable dynamics. Indiana Univ. Math. J. 57(2008), 1781–1788. http://dx.doi.org/10.1512/iumj.2008.57.3273Google Scholar
[11] Duncan, B. L. and Peters, J. R., Operator algebras and representations from commuting semigroup actions. Preprint, arxiv:1008.2244v1. Google Scholar
[12] Fowler, N. J., Discrete product systems of Hilbert bimodules. Pacific J. Math. 204(2002), 335–375. http://dx.doi.org/10.2140/pjm.2002.204.335 Google Scholar
[13] Hamana, M., Injective envelopes of operator systems. Publ. Res. Inst. Math. Sci. 15(1979), 773–785. http://dx.doi.org/10.2977/prims/1195187876 Google Scholar
[14] Kakariadis, E. T. A., Semicrossed products of C*-algebras and their C*-envelopes. Preprint, arxiv:1102.2252v2. Google Scholar
[15] Kakariadis, E. T. A. and Katsoulis, E. G., Semicrossed products of operator algebras and their C*-envelopes. J. Funct. Anal. 262(2012), 3108–3124. http://dx.doi.org/10.1016/j.jfa.2012.01.002 Google Scholar
[16] Laca, M., From endomorphisms to automorphisms and back: dilations and full corners. J. London Math. Soc. (2) 61(2000), 893–904. http://dx.doi.org/10.1112/S0024610799008492 Google Scholar
[17] Laca, M. and Raeburn, I., Semigroup crossed products and the Toeplitz algebras of nonabelian groups. J. Funct. Anal. 139(1996), 415–440. http://dx.doi.org/10.1006/jfan.1996.0091 Google Scholar
[18] Ling, K. and Muhly, P. S., An automorphic form of Ando's theorem. Integral Equations Operator Theory 12(1989), 424–434. http://dx.doi.org/10.1007/BF01235741 Google Scholar
[19] McAsey, M., Muhly, P. S. and Saito, K., Nonselfadjoint crossed products (invariant subspaces and maximality). Trans. Amer. Math. Soc. 248(1979), 38–409. http://dx.doi.org/10.1090/S0002-9947-1979-0522266-3 Google Scholar
[20] Mlak, W., Unitary dilations in case of ordered groups. Ann. Polon. Math. 17(1966), 321–328.Google Scholar
[21] Muhly, P. and Solel, B., An algebraic characterization of boundary representations. In: Nonselfadjoint Operator Algebras, Operator Theory, and Related Topics, Birkhäuser Verlag, Basel, 1998, 189–196.Google Scholar
[22] Murphy, G. J., Crossed products of C*-algebras by endomorphisms. Integral Equations Operator Theory 24(1996), 298–319. http://dx.doi.org/10.1007/BF01204603Google Scholar
[23] Nica, A., C*-algebras generated by isometries and Wiener–Hopf operators. J. Operator Theory 27(1992), 17–52.Google Scholar
[24] Paulsen, V. I., Completely bounded maps and operator algebras. Cambridge Stud. Adv. Math. 78, Cambridge University Press, Cambridge, 2002.Google Scholar
[25] Pedersen, G. K., C*-algebras and their automorphism groups. London Math. Soc. Monogr. 14, Academic Press, Inc., London–New York, 1979.Google Scholar
[26] Peters, J., Semicrossed products of C*-algebras. J. Funct. Anal. 59(1984), 498–534. http://dx.doi.org/10.1016/0022-1236(84)90063-6 Google Scholar
[27] Shalit, O. M., Dilation theorems for contractive semigroups. arxiv:1004.0723v1. Google Scholar
[28] Shalit, O. M., Representing a product system representation as a contractive semigroup and applications to regular isometric dilations. Canad. Math. Bull. 53(2010), 550–563. http://dx.doi.org/10.4153/CMB-2010-060-8 Google Scholar
[29] Solel, B., Representations of product systems over semigroups and dilations of commuting CP maps. J. Funct. Anal. 235(2006), 593–618. http://dx.doi.org/10.1016/j.jfa.2005.11.014 Google Scholar
[30] Solel, B., Regular dilations of representations of product systems. Math. Proc. R. Ir. Acad. 108(2008), 89–110. http://dx.doi.org/10.3318/PRIA.2008.108.1.89 Google Scholar
[31] Sz.-Nagy, B., Foias, C., Bercovici, H., and Kérchy, L., Harmonic analysis of operators on Hilbert space. Universitext. Springer, New York, 2010.Google Scholar
[32] Timotin, D., Regular dilations and models for multicontractions. Indiana Univ. Math. J. 47(1998), 671–684.Google Scholar
[33] Varopoulos, N. Th., On an inequality of von Neumann and an application of the metric theory of tensor products to operators theory. J. Funct. Anal. 16(1974), 83–100. http://dx.doi.org/10.1016/0022-1236(74)90071-8 Google Scholar