Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T10:22:07.222Z Has data issue: false hasContentIssue false
  • English
  • Français

Type Decomposition and the Rectangular AFD Property for W*-TRO’s

Published online by Cambridge University Press:  20 November 2018

Zhong-Jin Ruan
Zhong-Jin Ruan*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, U.S.A. e-mail: ruan@math.uiuc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the type decomposition and the rectangular 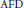$\text{AFD}$ property for 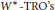${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$. Like von Neumann algebras, every 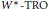${{W}^{*}}-\text{TRO}$ can be uniquely decomposed into the direct sum of 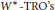${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of 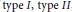$\text{type}\,I,\,\text{type}\,II$, and 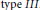$\text{type}\,III$. 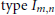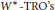We may further consider ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of $\text{type}\,{{I}_{m,n}}$ with cardinal numbers $m$ and $n$, and consider ${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$ of 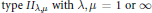$type\,I{{I}_{\lambda ,\mu }}\,\text{with}\,\lambda ,\,\mu \,=\,1\,\text{or}\,\infty $. It is shown that every separable stable 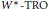${{W}^{*}}-\text{TRO}$ (which includes $\text{type}\,{{I}_{\infty ,\infty }}$, 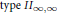$\text{type}\,I{{I}_{\infty ,\infty }}$ and 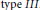$\text{type}\,III$) is 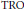$\text{TRO}$-isomorphic to a von Neumann algebra. We also introduce the rectangular version of the approximately finite dimensional property for 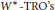${{W}^{*}}-\text{TRO }\!\!'\!\!\text{ s}$. One of our major results is to show that a separable 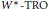${{W}^{*}}-\text{TRO}$ is injective if and only if it is rectangularly approximately finite dimensional. As a consequence of this result, we show that a dual operator space is injective if and only if its operator predual is a rigid rectangular 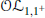$\mathcal{O}{{\mathcal{L}}_{1,{{1}^{+}}}}$ space (equivalently, a rectangular 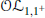$\mathcal{O}{{\mathcal{L}}_{1,{{1}^{+}}}}$ space).

Keywords

46L0746L0846L89
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 4 , 01 August 2004 , pp. 843 - 870
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Blecher, D., A new approach to Hilbert C*-modules. Math. Ann. 307(1997), 253–290.Google Scholar
[2] Blecher, D., A generalization of Hilbert modules. J. Funct. Anal. 136(1996), 365–421.Google Scholar
[3] Blecher, D., On selfdual Hilbert modules. Fields Institute Communications 13(1997), 65–80.Google Scholar
[4] Choi, M.-D. and Effros, E., Injectivity and operator spaces. J. Funct. Anal. 24(1977), 156–209.Google Scholar
[5] Connes, A., Classification of injective factors. Ann. of Math. 104(1976), 73–115.Google Scholar
[6] Dixmier, J., Les algèbres d’opérateurs dans l’espace hilbertien (algèbres de von Neumann). 2ième éd. Gauthier-Villars Éditeur, Paris, 1969.Google Scholar
[7] Effros, E., Ozawa, N. and Ruan, Z-J., On injectivity and nuclearity for operator spaces. Duke Math. J. 110(2001), 489–521.Google Scholar
[8] Effros, E. and Ruan, Z-J., spaces. Contemporary Math. 228(1998), 51–77.Google Scholar
[9] Effros, E. and Ruan, Z-J., Operator Spaces. London Mathematical Society Monographs 23, Oxford University Press, New York, 2000.Google Scholar
[10] Elliott, G. A. and Woods, E. J., The equivalence of various definitions for a properly infinite von Neumann algebra to be approximately finite dimensional. Proc. Amer. Math. Soc. 60(1976), 175–178.Google Scholar
[11] Exel, R., Twisted partial actions: A classification on regular C*-algebraic bundles. Proc. LondonMath. Soc. 74(1997), 417–443.Google Scholar
[12] Ghoussoub, N., Godefroy, G., Maurey, B. and Schachermayer, W., Some topological and geometric structures in Banach spaces. Mem. Amer. Math. Soc. 70(1987).Google Scholar
[13] Haagerup, U., A new proof of the equivalence of injectivity and hyperfiniteness for factors on a separable Hilbert space. J. Funct. Anal. 62(1985), 160–201.Google Scholar
[14] Hamana, M., Injective envelope of dynamical systems. Pitman Res. Notes Math. Ser. 271(1992), 69–77.Google Scholar
[15] Hamana, M., Triple envelopes and Šilov boundaries of operator spaces. Math. J. Toyama Univ. 22(1999), 77–93.Google Scholar
[16] Harris, L., A generalization of C*-algebras. Proc. LondonMath. Soc. 42(1981), 331–361.Google Scholar
[17] Junge, M., Nielsen, N., Ruan, Z-J. and Xu, Q., spaces–the local structure of non-commutative Lp spaces. Adv. Math. to appear.Google Scholar
[18] Kadison, R. and Ringrose, J., Fundamentals of the Theory of Operator Algebras, Vol. I and II. Academic Press, New York, 1983 and 1986.Google Scholar
[19] Kaplansky, I., Modules over operator algebras. Amer. J. Math. 75(1953), 839–858.Google Scholar
[20] Kaur, M. and Ruan, Z-J., Local properties of ternary rings of operators and their linking C*-algebras. J. Funct. Anal. 195(2002), 262–305.Google Scholar
[21] Kirchberg, E., On restricted perturbations in inverse images and a description of normalizer algebras in C*-algebras. J. Funct. Anal. 129(1995), 1–34.Google Scholar
[22] Kye, S-H and Ruan, Z-J., On local lifting property for operator spaces. J. Funct. Anal. 168(1999), 355–379.Google Scholar
[23] Lance, E. C., Hilbert C*-modules, A toolkit for operator algebraists. London Mathematical Society Lecture Note Series 210, Cambridge University Press, Cambridge, 1995.Google Scholar
[24] Murray, F. J. and von Neumann, J., On rings of operators, IV. Ann. of Math. 44(1943), 716–808.Google Scholar
[25] Ng, P-W. and Ozawa, N., A characterization of completely 1-complemented subspaces of non-commutative L 1 -spaces. Pacific J. Math. 205(2002), 171–195.Google Scholar
[26] Paschke, W., Inner product modules over B*-algebras. Trans. Amer. Math. Soc. 182(1973), 443–468.Google Scholar
[27] Paulsen, V., Completely Bounded Maps and Dilations. Pitman Research Notes Math. Ser. 146(1986).Google Scholar
[28] Pisier, G., An introduction to the theory of operator spaces. London Mathematical Society Lecture Note Series 294, Cambridge University Press, Cambridge, 2003.Google Scholar
[29] Pisier, G. and Xu, Q., Non-commutative martingale inequalities. Comm. Math. Physics, 189(1997), 667–698.Google Scholar
[30] Rieffel, M., Induced representations of C*-algebras. Adv. in Math. 13(1974), 176–257.Google Scholar
[31] Rieffel, M., Morita equivalence for C*-algebras and W*-algebras. J. Pure and Appl. Alg. 5(1974), 51–96.Google Scholar
[32] Ruan, Z-J., On matricially normed spaces associated with operator algebras. Ph.D thesis, UCLA, 1987.Google Scholar
[33] Ruan, Z-J., Injectivity of operator spaces. Trans. Amer. Math. Soc. 315(1989), 89–104.Google Scholar
[34] Smith, R., Finite dimensional injective operator spaces. Proc. Amer. Math. Soc. 128(2000), 3461–3462.Google Scholar
[35] Takesaki, M., Theory of operator algebras, I. Springer-Verlag, New York, 1979.Google Scholar
[36] Takesaki, M., Theory of operator algebras, III. Encyclopedia of Mathematical Sciences, 127, Springer-Verlag, Berlin, 2003.Google Scholar
[37] Wittstock, G., Extensions of completely bounded C*-module homomorphisms. Monogr. Stud. Math. 18(1983), 238–250.Google Scholar
[38] Youngson, M. A., Completely contractive projections on C*-algebras. Quart. J. Math. Oxford Ser. 34(1983), 507–511.Google Scholar
[39] Zettl, H., A characterization of ternary rings of operators. Adv. in Math. 48(1983), 117–143.Google Scholar