Abstract
The impulsive heating events and their corresponding nonlinear dynamics remain one of the most obscure physical processes in solar atmospheric physics. The complicacy of these processes together with limited observations have greatly hampered our understanding of them. Here, we present, for the first time, an unambiguous example of a nonlinear acoustic wave in a closed coronal loop or loop segment, which appeared as a fast propagating ultra-hot disturbance cohesively in an indistinguishable corona loop with a highly evolving emission intensity profile. Based on the theory of propagating nonlinear waves, we argue that this type of observation can provide further information for the disturbance during its propagation. With this information, we conclude that the propagating nonlinear disturbance can quickly heat the corona through the rarefaction wave, and the disturbance-induced magnetic reconnection should not happen in our observation. Besides, a convenient criterion has also been deduced for the existence of the disturbance-induced reconnection mechanism. All of this provides us with a new insight into the accompanying nonlinear dynamics of solar impulsive heating events, which can not only shed light on problems including coronal heating and the fast formation of hot coronal loops, but also show us a very novel and prospective seismology scheme for the diagnosis of coronal plasma properties.
Export citation and abstract BibTeX RIS
1. Introduction
One of the main scientific objectives of the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) is to investigate the physical nature of the fast and drastic variations of the extreme ultra-violet (EUV) spectral irradiance in the solar atmosphere, which have been widely accepted as important sources of disturbance for the space weather (Groth et al. 2000; Knipp 2005; Schwenn et al. 2005; Schrijver & Siscoe 2010; Chen 2011). The understanding of the physical nature of these fast and drastic EUV spectral variations is important not only in the context of solar atmospheric physics but also in magnetized plasma physics, in examining the heating mechanism of stellar atmosphere and forecasting the space weather near the Earth (Aschwanden 2005, 2019; Colak & Qahwaji 2009; Priest 2014). However, the process has been long hampered by the physical complicacy of the phenomena and the difficulty of inversing physical properties of the corona from limited spectral observations (Aschwanden 2005; Reale et al. 2011; Cheng et al. 2012; Huang et al. 2014; Reale 2014; Gou et al. 2015; Cargill et al. 2016; Li et al. 2018b, 2018d, 2019; Wang et al. 2018; Yuan et al. 2019).
The observational detection of various types of wave phenomena provides us with an alternative option for the determination of unknown parameters of the corona (Uchida 1970; Aschwanden 1987; Aschwanden et al. 1999; Nakariakov & Verwichte 2005; De Moortel & Brady 2007; Roberts 2008; Liu et al. 2012; Guo et al. 2015; Jain et al. 2015; Thackray & Jain 2017; Goddard et al. 2018; Li et al. 2018a, 2018c; Pascoe et al. 2018; Zhang et al. 2018; Anfinogentov & Nakariakov 2019; Shen et al. 2019a; Zheng et al. 2019). However, most of the reported cases are interpreted as linear waves (Roberts et al. 1984; Nakariakov & Verwichte 2005; Yuan & Van Doorsselaere 2016; Li & Liu 2018). The propagating nonlinear disturbances with the corresponding nonlinear dynamics are rarely reported in spite of their important role in the impulsive heating of events (Nakariakov & Verwichte 2005; Attrill et al. 2007; Priest 2014; Shen et al. 2018, 2019a; Liu et al. 2019; Mohan et al. 2019). Here, we present, for the first time, a clear observation of a fast propagating ultra-hot disturbance captured by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board SDO in a limbic coronal loop, which is unambiguously identified as a fast propagating nonlinear acoustic wave and is also shown to provide reliable physical information that can significantly improve our knowledge of the corresponding coronal nonlinear dynamics of the widely observed impulsive heating event.
2. Observation and Methods
2.1. SDO/AIA Data
The AIA provides continuous full-disk images of the solar atmosphere in seven EUV pass-bands ranging from 94 to 335 Å with a temporal resolution of 12 s and a spatial resolution of 0
6. The analyzed sequences began at 05:30 UT on 2017 September 9. The data has been prepared to level 1.5 by the standard AIA preparing routine "aia_prep.pro" included in the SolarSoftWare (SSW) system, and a log transformation has been carried out for the visualization. The log transformation is carried just for image visualization, and all spectral analyses are based on the original data.
The presented propagating disturbance occurred upon the active region numbered as NOAA 12673 by the National Oceanic and Atmospheric Administration (NOAA) Space Weather Prediction Center near the western limb of the Sun (see Figure 1). To observe the dynamic progress of the present event, subregions including the considered active region were extracted and an animation (see Figure 1) about the subregions was created. It shows that the propagating disturbance was induced by a jet flow following an impulsive heating event in the northern foot of the investigated loop. The dynamic properties of the jet flow are estimated mainly from the AIA 304 Å observation. In addition, it also shows that the propagating disturbance appeared only in the two EUV pass-bands, i.e., 94 and 131 Å whose thermal respond profiles exclusively possess respond peaks near 107relative to the other AIA EUV pass-bands. The observations from all EUV pass-bands of AIA that assisted with their thermal responses are used to study the propagating disturbance of interest. The differential emission measure (DEM; Cheng et al. 2012) analysis and the propagating features of the disturbance are used to provide information of disturbed and undisturbed plasma, which can not only reveal the coronal heating mechanism behind the propagating nonlinear acoustic wave, but also provide a convenient criterion for the magnetic reconnection induced by a nonlinear acoustic wave. The scenario may not even happen in the present case.
Figure 1. Overview and closeup view of active region NOAA 12673. Left: synthetic full-disk solar image with 211, 193, and 171 Å data shown in its red, green, and blue channels, respectively. Right: a closeup view of the considered active region with the trajectory of the propagating disturbance is marked by the white curve and colored arrows in AIA 94 Å closeup image. An animation created from AIA EUV coronal observation is available. The animated images show the temporal evolution of the propagating ultra-hot disturbance. The propagating disturbance is marked as a series of colored arrows in AIA 94 and 131 Å panels. The animation runs from 05:30 to 06:27 UT.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution image2.2. DEM Analysis
The DEM curves are computed based on six AIA EUV pass-bands (the optically thick passband of 304 Å is excluded) by using the "xrt_dem_iterative2.pro" routine in the SSW system. The routine carries a Levenberg–Marquardt least-squares fitting to obtain DEM curves from a set of spectral data points and introduced to compute the DEM curve based on AIA observation by Cheng et al. (2012). Similar to Cheng's approach, we also used 100 Monte Carlo realizations to reduce uncertainty.
2.3. Extraction of the Disturbance's Intensity Profile
There are several horizontal bright ribbons in the time–distance diagrams (Figure 3) along the trajectory of the propagating disturbance, and they are background structures that intersect with the considered trajectory. Thus, the intensity profiles shown in Figure 6 were extracted from a detrending time–distance diagram to reduce the effect of the background structures. The detrending time–distance diagram was obtained by removing a 40 pixel boxcar smoothed background from the original time–distance diagram.
3. Results
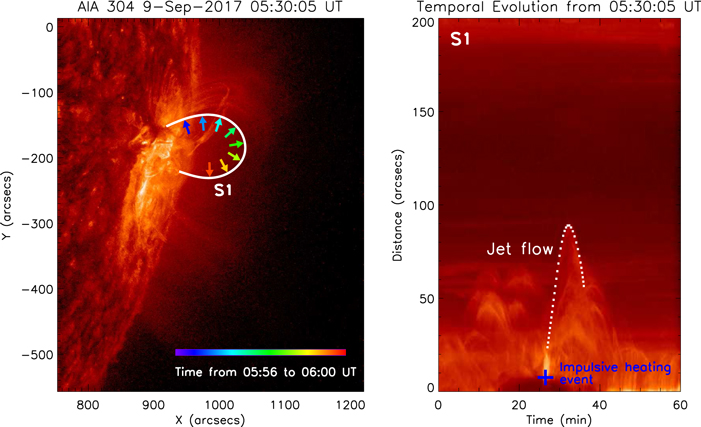
The considered disturbance propagated cohesively in a closed coronal loop that is well plying up the preexisting loop system. The coronal loop was blended with the dispersed bright corona at the seven AIA EUV pass-bands before the appearance of the disturbance (see Figure 1), and then was outlined by the propagating disturbance obviously at the AIA 94 and 131 Å bandpass. The data from a 5 pixel wide slit along the coronal loop (S1 in Figure 2) was extracted, averaged in the width direction, and stacked chronologically to form time–distance diagrams. From the AIA 304 Å time–distance diagram (right panel in Figure 2), which is often used to study materials with lower temperature (about 105±0.5 k) in the solar atmosphere (Li et al. 2018b, 2018c; Shen et al. 2019b), we can see there are several jet flows during the investigated time interval. Based on the temporal and spatial correspondences between the propagating disturbance and these jet flows, it can be easily confirmed that (1) the propagating disturbance is accompanied by the jet flow with the highest apex among all these presented jet flows, and (2) both the propagating disturbance and its corresponding jet flow are initialized in response to an impulsive heating event at the northern foot of the coronal loop (marked as a blue plus sign in Figure 2's right panel). Within this work, we primarily focused on the propagating disturbance.
Figure 2. Temporal evolution of cooler plasma. Left: AIA 304 Å image showing material with lower temperature above active region NOAA 12673, where (as in Figure 1) their trajectory (S1) of the propagating disturbance is marked by a white curve and a set of colored arrows with the color denoting the time order. Right: the AIA 304 Å time–distance diagram of S1 showing the temporal evolution of low temperature plasma (ranging in 105±0.5 k), in which the jet flow and impulsive heating site are indicated by the white dotted curve and the blue plus sign.
Download figure:
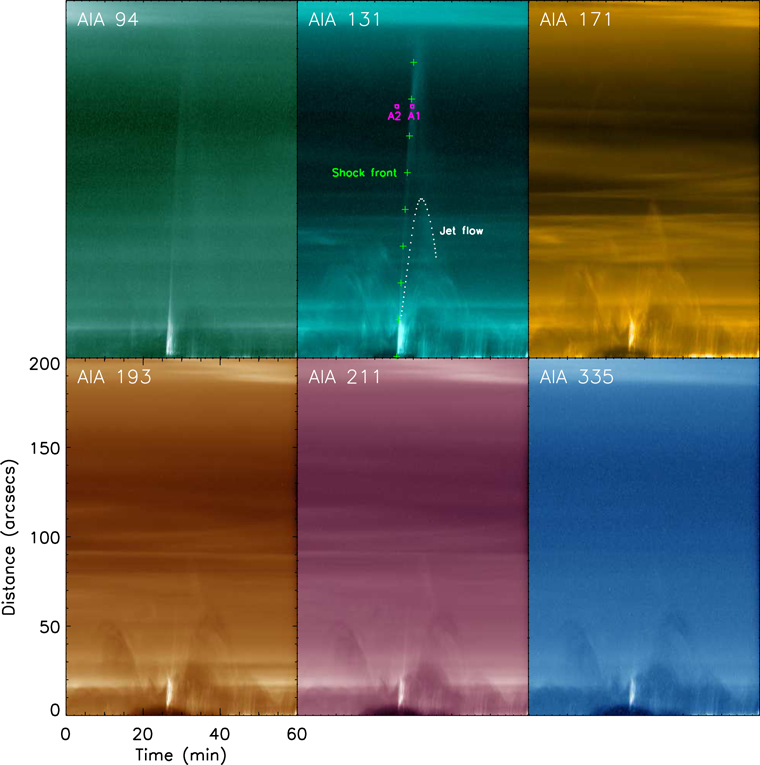
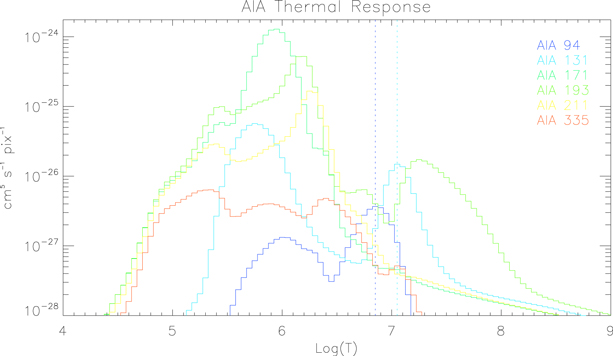
Standard image High-resolution imageOne striking feature of the propagating disturbance is that it only appeared at AIA 94 and 131 Å bandpasses in an indistinguishable loop among all AIA coronal observations (see Figure 3). This strongly suggests that the propagating disturbance should have a characteristic temperature near the shared and exclusive respond peak (near 107 k, indicated by vertical lines in Figure 4) of 94 and 131 Å bandpasses. Moreover, it also suggests from the disturbance appeared in an indistinguishable coronal loop that the undisturbed region of this propagating disturbance should have a typical characteristic temperature (about 106 k) of ordinary background corona over active regions (Aschwanden 2005; Reale 2014). In order to confirm the conjecture, we extracted two types of regions (taking A1 and A2 in Figure 3 as representatives), which respectively correspond to the undisturbed and disturbed regions, for the DEM analysis (Cheng et al. 2012). The result of the DEM analysis, as shown in Figure 5, is consistent with our conjecture. The mean DEM curve of 100 MC solutions at the disturbed region shows double crests with one peaked at 2.0 × 106 K and the other peaked at 1.6 × 107 K. While the mean DEM curve of 100 MC solutions at the undisturbed region shows only one crest peaked in 2.0 × 106 K. We notice that there is a very slight increase near 107 K in the mean DEM curve of the undisturbed region, which should be influenced by the neighboring high temperature loop of the selected region, even though we have selected a relatively pure region for the investigation. Nevertheless, one can be sure that there is a mass of significant ultra-hot material appearing in the considered region after the passage of the disturbance. This strongly indicates that the disturbed plasma is significantly different from its undisturbed state, and the present propagating disturbance should be a distinctly nonlinear wave (Priest 2014).
Figure 3. Time–distance diagrams of S1 at six AIA EUV bandpasses showing temporal evolution of the propagating disturbance, where the front of the disturbance is indicated by the green plus signs and the accompanying jet flow of the disturbance (see Figure 2) is overplotted as the white dotted line in the AIA 131 Å panel. The two subregions of A1 and A2 are selected for further analysis, representing disturbed and undisturbed regions, respectively.
Download figure:
Standard image High-resolution image
Figure 4. AIA thermal response profiles for six AIA coronal bandpasses. The exclusive and neighboring peaks of 94 and 131 Å are indicated by two vertical dotted lines.
Download figure:
Standard image High-resolution image
Figure 5. DEM curves of subregions marked in Figure 3 (A1 on the top and A2 on the bottom), where solutions of 100 MC realizations and their average are plotted as the black solid lines and the green solid lines, respectively.
Download figure:
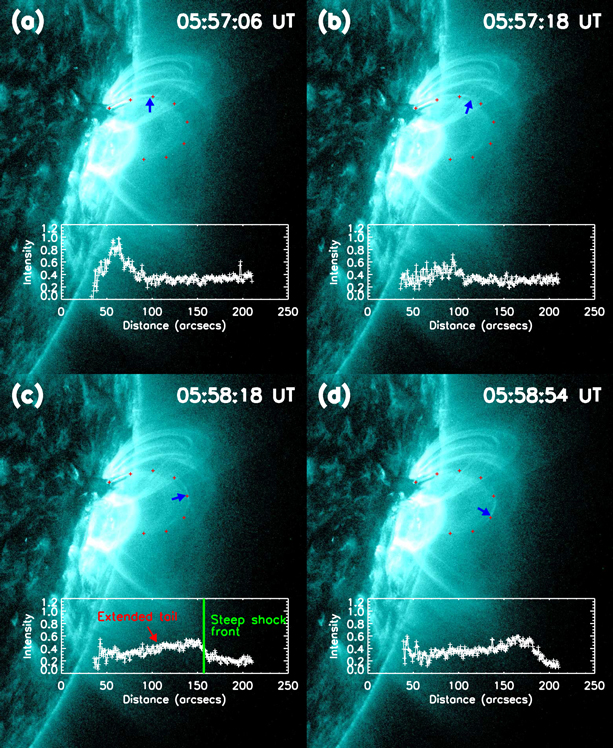
Standard image High-resolution imageBesides the distinct feature in temperature, the temporal evolution of the 131 Å intensity profile along the propagating direction of the disturbance provides good support for the nonlinear conjecture too. It can be seen clearly from the 131 Å time–distance diagram (shown in Figure 3) that the disturbance appeared as a narrow strip with two sharp edges at the beginning, and then its tail was gradually extending and smoothing when its front was still sharp during its propagation. A closed-up view of this phenomenon is shown in Figure 6. This result is greatly consistent with the classical picture of propagating nonlinear acoustic wave that shows a sharp wave front (i.e., shock front) tightly followed by a gradually expanding and smoothing trail corresponding to the rarefaction wave (Priest 2014).
Figure 6. Temporal evolution of the AIA 131 Å intensity profile along S1 overlying the bottom region of corresponding AIA 131 Å images as a series of white plus signs. On the background images, S1 and the front of the disturbance are marked in AIA images as a series of red plus signs and blue arrows. In panel (C), the steep shock front and the extended tail of the disturbance are indicated by the red arrow and the green vertical line, respectively. Note that all intensity profiles are uniformly normalized by the maximum and minimum values of the four sets of data.
Download figure:
Standard image High-resolution imageMoreover, the propagating speed of the disturbance is also investigated and the result supports the nonlinear conjecture again. The disturbance propagated with a very fast and nearly constant projected velocity estimated as 652 ± 15 km s−1 from an average of 10 measurements. The velocity is very unusual for an optics observable propagating disturbance along the closed magnetic line in the dispersed bright corona. It significantly exceeds the situ acoustic velocity of the typical dispersed corona (≈150 km s−1 for 106 k). As we all know, a nonlinear wave, i.e., a shock wave, could appear when the propagating velocity of the disturbance is significantly larger than the acoustic velocity of the medium where it propagates (Nakariakov & Verwichte 2005; Salas 2007; Priest 2014). Note that the possibilities of fast modes in the linear regime, such as the classical Alfvén wave or torsional Alfvén wave and the fast kink or sausage waves in the flux tube, have been pre-excluded because they cannot disturbed the plasma, especially for its thermal properties, so significantly in situations where the linear approximation is permitted (Aschwanden 1987; Priest 2014; Yuan & Van Doorsselaere 2016).
Finally, it should also be worth noting that the disturbance propagates cohesively in a coronal loop and does not show any significant lateral leakage. As for a point-exciting, directionally propagating, and highly nonlinear wave, possibilities of modes strongly coupling to the magnetic field, such as the derivative Alfvén series, the well-known sausage modes and the like, can be ruled out, because they all have distinct lateral leakage due to the ponder-motive force caused by the significant magnetic changes carried by them (Thurgood & McLaughlin 2013; Shestov et al. 2017; Verwichte et al. 2017), as a result of which they usually manifest as one or trains of gradually expanding arc-like wave fronts perpendicular to their directions of propagation (Thurgood & McLaughlin 2013; Shen et al. 2018). Theoretically, the only mode that can meet both requirements on the propagating direction and disturbance scale is the nonlinear acoustic wave in a regime of low β magnetized plasma, such as a typical EUV bright solar corona, where the magnetic field is strong enough to keep the propagating disturbance from leaking laterally. We, therefore, conclude that the observed directionally propagating disturbance is most likely a typical nonlinear acoustic wave on the basis that it was unambiguously confirmed as a significantly nonlinear one.
4. Discussion
4.1. The Nonlinear Waves in the Solar Corona
Since they can not only act as good energy transmitters and atmospheric perturbators in the corona, but also provide a wealth of physical information about their excitation source and propagating medium, propagating disturbances have been a great attraction in the corona to solar physicists for many years (Uchida 1970; Aschwanden 1987, 2019; Nakariakov & Verwichte 2005; Priest 2014; Reale 2014). According to their physical characteristics, the scientific significance of studying propagating disturbances primarily lies in two aspects. The first is that the propagating disturbance itself is one of important forms of energy transmission, which can transmit energy through the solar atmosphere and perturb the medium where it propagates (Attrill et al. 2007; Priest 2014; Shen et al. 2018, 2019a; Liu et al. 2019). The second is that the physical information it carries may make it a potential diagnostic tool for solar atmospheric parameters (Uchida 1970; Aschwanden 1987, 2019; Nakariakov & Verwichte 2005; Shen et al. 2018).
Generally, propagating disturbances caused by point-exciting sources can be classified into two categories in magnetized plasma on account of the existence of the magnetic field, i.e., the directional one and the non-directional one, depending on the propagating direction of the disturbance (Nakariakov & Verwichte 2005; Priest 2014; Aschwanden 2019). Within these two categories, the strictly directional propagating disturbance refers to that propagating cohesively in one direction, mostly the direction of the magnetic field, which is believed to penetrate longer distance, and thus have more significance of coronal seismology (Aschwanden 1987; Nakariakov & Verwichte 2005; Roberts 2008; Priest 2014). As for the strictly directional propagating disturbances, there are types of them that have been discovered (Roberts et al. 1984; Aschwanden 1987; Roberts 2008; Priest 2014). However, both them are under the linear regime. Theoretically, many impulsive heating events can effectively disturb their surroundings on the order of magnitude far beyond the undisturbed value and then excite nonlinear propagating disturbances (i.e., nonlinear waves). Those nonlinear waves usually possess more energy and more destructibility, but are more complex and often mixed with other associated phenomena (Priest 2014; Aschwanden 2019). Therefore, many present studies have focused on the linear propagating disturbance. For details about the physical nature of those impulsive heating induced nonlinear propagating disturbances, what specific effects they have on their propagating medium, and what physical information they can provide, there is still no satisfactory answer (Aschwanden 1987, 2019; Nakariakov & Verwichte 2005).
4.2. The Present Propagating Disturbance
In this study, we present a clear observation of an ultra-hot directionally propagating disturbance at two high temperature AIA EUV pass-bands (94 and 131 Å) that propagates with a fast and constant velocity of 652 ± 15 km s−1 cohesively in typical dispersed active corona (or an indistinguishable dispersed coronal loop in other words), which is really unusual from the existing cases of directionally propagating disturbances and is most likely to be a full new mode, i.e., the nonlinear acoustic wave that is well grounded by the classical MHD theory but has been long overlooked due to the lack of clear observational evidence (Priest 2014). There are indeed cases of directionally propagating disturbances reported and even some of them were also suspected as the nonlinear propagating disturbances, but both of them show the propagating disturbances and their host coronal loops in the same passband (Liu et al. 2012; Hou et al. 2018; Shen et al. 2018, 2019a). With respect to those suspected nonlinear propagating disturbances, we would like to propose that the observational emission intensity and its corresponding physical properties do not have a linear relationship, but a complex relationship. Significant variation of special passband emission intensity, therefore, does not have to mean a significant variation of plasma's physical properties, and can hardly be a reliable criterion for nonlinear wave. In classical nonlinear wave theory, the nonlinear wave is that for which propagating disturbance quantities are comparable or even much larger than the undisturbed quantities (Priest 2014). Hence, we suggest that it is more likely to be nonlinear for cases whose disturbances appear in an indistinguishable dispersed corona or in a coronal loop at a different passband. In order to obtain a further convincing judgment, three in-depth quantitative analyses have also been carried out for the present event. They are the DEM analysis on the disturbed and undisturbed regions, the evolutionary analysis on the spatial distribution of disturbance emission intensity, and the theoretical analysis on the disturbance propagating velocity, respectively. The results of these three analyses, as shown in the last section, are both consistent with a nonlinear acoustic wave conjecture; we, therefore, have reasons to believe that the present case should be the most unambiguous instance of the propagating nonlinear acoustic wave at the current stage, which naturally indicates that a nonlinear acoustic wave can indeed be excited by the impulsive heating event and freely propagate in the upper solar atmosphere, which is consistent with and further confirms the widely accepted low β approximation of plasma for the typical EUV bright corona.
4.3. Potential Implications of the Present Case
The present case can not only show us a good example of the propagating nonlinear acoustic wave, but also provide us with a good opportunity to study the nonlinear physical process in detail. Within this study, we suggest at least three aspects deserving comment.
4.3.1. Criteria for the Propagating Nonlinear Acoustic Mode
First of all, based on the observational characteristics of our case, four criteria emerge for the identification of the propagating nonlinear acoustic mode: (1) the disturbance propagates directionally along a definite trajectory without significant lateral leakage, (2) the propagating disturbance and it host appear in different pass-bands that have significantly different characteristic temperatures, (3) its spatial profile (i.e., waveform) of emission intensity at a special passband should be evolving rapidly and a typical image is a shock wave following with a gradually elongating rarefaction wave, and (4) its propagating velocity is most likely significantly greater than the acoustic velocity of its host. We also caution that these criteria may not be sufficient when used alone, but make a lot of sense when combined together.
4.3.2. Implications of the Nonlinear Coronal Seismology
Although the nonlinear waves are more complex, they are subject to more restrictions, which means more information. As for a nonlinear acoustic wave, plasma parameters (e.g., temperature, pressure, and density) can be restricted by the well-known Rankine–Hugoniot conditions (Rankine 1869; Hugoniot 1887; Salas 2007; Priest 2014), which can theoretically provide three limiting equations and can significantly reduce the free parameters of physical states between two sides of the jump. These conditions, when used in our case where the disturbance is propagating along the magnetic field line in the tenuous corona with a significantly larger deviation from its propagating medium, show a brighter prospect. Since the magnetic field decouples from MHD equations for one-dimensional hydrodynamics of the plasma along magnetic field lines, the physical states between two sides of a hydrodynamic shock front can be described as the well-known Rankine–Hugoniot conditions. For a inertial reference frame where the undisturbed gas is still, the Rankine–Hugoniot conditions can be written as
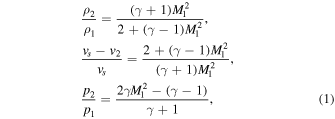
where, ρ1, ρ2, p1, p2, and v2 indicate densities of undisturbed and disturbed plasma, thermal pressures of undisturbed and disturbed plasma, and the fluid velocity of disturbed plasma, respectively. vs and γ indicate the shock velocity and the ratio of specific heats (usually taken as 5/3 for coronal plasma). M1 indicates the ratio of shock velocity vs to in situ acoustic velocity, i.e., 
, of the undisturbed plasma. Dividing the bottom equation by the top equation of Rankine–Hugoniot conditions, we obtain that
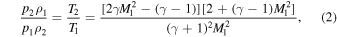
where T1 and T2 (i.e., Tp of propagating disturbance) indicate temperature of undisturbed and disturbed plasma. When substituting the disturbance temperature from the DEM analysis and its propagating velocity into this equation, we can easily obtain that the estimated temperature ahead of the disturbance is 1.4 × 107 k and M1 is 1.1. This suggests that the observed disturbance should be a mild nonlinear acoustic wave propagating in an evacuated hot loop. However, the result is strongly in conflict with the clear change of emission in AIA 94 and 131 Å bandpasses, which implies that the density of hot plasma should have a significant change during the passage of the disturbance, but the density ratio of ρ2/ρ1 is given as 1.1 for M1 = 1.1 by according to the Rankine–Hugoniot conditions. Besides, the result is also inconsistent with the highly evolving emission intensity profile. In addition, a filling process of an evacuated hot loop cannot explain the observation because the process should show a dispersed front and a prolonging body extending to the photosphere without a clear tail (Reale 2014), which is distinctly different with the observation. Beyond that, the evacuated hot loop, if in existence, should be very unstable and tend to fill up quickly (Reale 2014), which is also in conflict with the fact that the undisturbed loop shows few changes for a relatively long period before the passage of the disturbance. We, thus, suggest that this may be caused by the inaccurate temperature obtained from the DEM analysis for the limited observation, especially when considering that the observation of the hotter region (T > 107 k) is less than the region where the temperature ranges from 105 to 107 k (see the Figure 4).
On the other side, it is reasonable that the loop might be a dispersed EUV bright corona, whose temperature is also obtained from the DEM analysis and is 1.6 × 106 k. When substituting this as T1 into Equation (2), we can obtain a different T2 that is 7.6 × 106 and a distinct M1 that is 3.1, which is obviously more consistent with the present observation. We, therefore, would like to believe that this may be the more likely solution. While, we have to admit that there is a certain deviation on the disturbance temperatures estimated from the DEM analysis and this scheme (about 0.3 in the logarithmic scale), it should be acknowledged that this is reasonable at the current level of observation, especially when considering the relatively large systematic error of the DEM analysis and the considerable broadening of the crests on DEM curves. Nevertheless, this provides us with a quantitative comparison of two schemes.
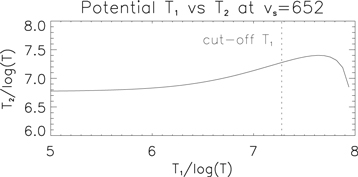
Moreover, couples (as shown in Figure 7) of potential T1 and T2 can be obtained from Equation (2) with only the observed propagating velocity of the disturbance, which is directly measured and shows small uncertainty. Since the disturbance cannot propagate slower than the acoustic velocity of its medium, there is a cutoff T1 (see the vertical dashed line in Figure 7), in which the disturbance propagates in the acoustic velocity of its medium. From the potential curve of T1 versus T2, we can see that the dependency of T2 gradually weakens with decreasing T1, because the propagating velocity of a drastic nonlinear acoustic wave mainly depends on the temperature of its disturbed plasma, which may provide us with a prospective way to estimate the disturbance temperature with less information according to a simplified version of Equation (2) for disturbances that propagate in a significant nonlinear acoustic mode. The simplified equation is T2 = 
where c gradually decreases its dependence on M1 as M1 increases, e.g., c = 17.8 ± 4.4 for 
. This also indicates that the disturbance temperature is more likely less than 107 k, which is also closer to both response peaks of the 94 and 131 Å bandpasses. Here, we would also like to note that since a distinct change in any thermal parameters of plasma manifest a large M1, this should be a more flexible scheme and could be used in a broader situation.
Figure 7. Potential T1 vs. T2 for the observed propagating velocity of disturbance, where the cutoff T1 is plotted as the vertical dashed line, in which the disturbance propagates in the acoustic velocity of the undisturbed plasma.
Download figure:
Standard image High-resolution image
Furthermore, it is worth noting that the temporal evolution of the disturbance's peak temperature could be estimated according to 
for a relatively uniform undisturbed region in both linear and nonlinear modes, where the subscripts of 1 and 2 indicate values in different moments during the propagation of the disturbance. This may be used to study the temporal evolution of temperature during the propagation of a disturbance. We also notice that the projection effect is ignored for this estimation and such neglect should be justified in the present case, because the propagating front did not show a significant curved trajectory in the time–distance diagrams (see Figure 3), which would occur when the projection effect has a significant influence on the projected velocity as a result of the curvature of the magnetic line itself.
4.3.3. Implications on the Coronal Nonlinear Dynamics
Based on the mentioned deduction, two critical implications of the coronal nonlinear dynamics behind the propagating disturbance can also be obtained from the present observation.
The first implication is that the peak temperature of the disturbance should change slightly (less than 5% when considering the undisturbed region has a similar temperature that is reasonable for a typical dispersed EUV bright coronal loop) during the observation based on the deduction that the change of peak temperature is proportional to the change of the propagating velocity for the propagating nonlinear acoustic wave, and due to the negligible variation of the disturbance's propagating velocity during the observation. On account of the implication, a long-standing scenario of coronal heating mechanism is excluded in the present case. The scenario is the disturbance-induced magnetic reconnection as a secondary coronal heating source (Attrill et al. 2007). It is excluded because the peak temperature of the disturbance did not significantly increase during the observation that obviously contradicts the secondary energy release process in the disturbance-induced magnetic reconnection scenario. It should be mentioned that the conclusion is mainly for the present case and it does not negate the possibilities of the scenario on the other cases. As for other cases, we also propose that a significant increase of the propagating velocity of the propagating nonlinear acoustic wave should imply the existence of an additional heating mechanism, such as the disturbance-induced magnetic reconnection.
The other implication indicates a new detail of coronal heating processes caused by the coronal nonlinear dynamics. It indicates that the rarefaction wave behind the shock front should play a crucial role in the heating of its propagating medium, which, to be specific, can fast heat the plasma by continuously prolonging the disturbed region during the propagation of the disturbance. This further provides a fast formation mechanism for the widely observed high temperature coronal loops that appear immediately after impulsive heating events.
Finally, it should be mention that these implications, as new discoveries on the nonlinear dynamics for plasma in an extreme condition, should provide clues to not only the present situation but also any situation where the nonlinear acoustic wave may be involved.
In summary, we report a clear observation of a fast propagating ultra-hot disturbance cohesively in the indistinguishable corona above the active region NOAA 12673 captured by the SDO/AIA. Thanks to the continuous, multiband, and high quality data set of AIA, both radiative, spatial, and temporal observational features of the propagating disturbance have been analyzed in detail. The results consistently indicate that the present propagating disturbance should be a typical instance of the nonlinear acoustic wave and provide us in turn with four valuable criteria for the nonlinear acoustic wave. Based on the observation, a theoretical analysis has also been carried out. From the analysis, we find a novel seismology scheme for the nonlinear acoustic wave, which implies a very prospective way to diagnose the temperature of the disturbed gas from the propagating velocity of a nonlinear acoustic wave with only a weak dependence on other parameters. By using the scheme in the present observation, two critical implications on the nonlinear dynamics behind the propagating disturbance have also been obtained. All of these provide a new insight into the accompanying nonlinear physical dynamics of impulsive heating events in solar atmosphere, which significantly advances our knowledge of the nonlinear dynamics of the solar atmosphere and sheds light on questions with respect to nonlinear dynamics of plasma in extreme space conditions that would be of interest to a broader astronomical audience.
The authors are greatly indebted the anonymous referee for constructive comments. We are grateful for the observation provided by the SDO, which is a mission for NASAs Living With a Star (LWS) Program. This work is supported by grants from the National Scientific Foundation of China (NSFC 11903016, 41674170, 41974197, 41874204, and 41804163) and by Excellent Team of Spectrum Technology and Application of Henan Province (grant No. 18024123007).