Determining the Nanoflare Heating Frequency of an X-Ray Bright Point Observed by MaGIXS

Understanding the heating of the nonflaring solar corona is an active topic of research in heliophysics. It is well accepted that magnetic fields are mainly responsible for coronal heating. The photospheric driver randomly moves the footpoints of the magnetic field lines and either generates waves or the quasi-static buildup of magnetic energy, depending on the timescale of motion (Klimchuk 2006). Heating by the dissipation of the magnetic energy (e.g., Parker 1988) is termed DC heating, while the dissipation of waves (e.g., Alfvén 1947) is known as the AC heating mechanism. Both the AC and DC heating mechanisms can lead to impulsive heating events, termed nanoflares (Klimchuk 2015). The magnitude and frequency of these nanoflares determine whether they can adequately satisfy the coronal heating budget. Thus, it is of great importance to study the nanoflares and determine their frequency to validate their role in coronal heating. According to the occurrence frequency, the nanoflares are primarily classified into two different categories: high-frequency (HF) nanoflares and low-frequency (LF) nanoflares. HF nanoflares are when the cooling timescale is short compared to the time between two successive heating events. The plasma could not cool enough in between the events, and in this case, the plasma would be heated quasi-steadily. On the other hand, for the LF nanoflare heating, the plasma would be cooled significantly before successive events. Determining the properties of the nanoflares from the observations would significantly constrain the properties of the heating mechanism.

Due to the small, faint, and transient nature of the nanoflares, their direct observation by current-generation instruments is limited by several factors, including inadequate instrumental spatial resolution, cadence, and spectral information. To infer and validate the nanoflare heating scenario, in the absence of direct observations, researchers have often used different plasma diagnostics, e.g., the emission measure (EM) distribution (Reale et al. 2009; Testa et al. 2011; Tripathi et al. 2011; Warren et al. 2011, 2012; Winebarger et al. 2011; Testa & Reale 2012; Brosius et al. 2014; Caspi et al. 2015; Del Zanna et al. 2015; Ishikawa et al. 2017), the variability of the footpoint emission (Testa et al. 2013, 2014), and time-lag analysis (Viall & Klimchuk 2012, 2017). The EM distribution, which indicates the amount of emitting plasma at different temperatures, is a useful diagnostic for parameterizing the frequency of energy deposition. Several observational and theoretical studies (e.g., Carole 1976; Cargill 1994; Cargill & Klimchuk 2004; Warren et al. 2012) have suggested that EM has a peak at an average plasma temperature (for active regions, or ARs, 3-4 MK) along with cool and hot components.

For a better understanding of the frequency and observable properties of nanoflare heating, several earlier studies have compared the observed intensities, EM distribution, and/or other observable quantities with the simulated nanoflare-heated plasma. For example, Barnes et al. (2019, 2021) compared the EM distributions and time lags of simulated nanoflare-heated plasma of ARs with the observed distribution derived from extreme-ultraviolet (EUV) observations by the Atmospheric Imaging Assembly (AIA: Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012). Their study suggests that HF nanoflares dominate the core of the AR. Warren et al. (2020) compare the modeled EM of an AR with the derived EM from EUV observations of the High-resolution Coronal Imager (Hi-C) sounding rocket experiment. They also found that HF heating provides the best match to the observed EM. Recently, Mondal et al. (2023) studied the average nanoflare frequency for heating coronal X-ray-bright points (XBPs) by comparing the simulated EM distribution with the observed distribution. For an accurate estimation of the observed EM distribution at higher temperatures, they combine the EUV observations of SDO/AIA with the moderate-energy-resolution disk-integrated X-ray spectra observed by the Solar X-ray Monitor (XSM: Mithun et al. 2020a, 2020b; Mondal et al. 2021; Vadawale et al. 2021) on board Chandrayaan-2. They found a good match of the observed EM distribution at coronal temperatures with the simulated distribution of nanoflare-heated plasma. These nanoflares had multiple frequencies, and their energy distribution followed a power-law slope close to −2.5. However, as XSM provides the disk-integrated spectrum, it is not efficient for deriving the EM distribution for a single coronal feature (e.g., a single AR or XBP). Studying the heating frequency in great detail for a single AR or XBP requires sensitive spatially resolved spectroscopic observations in EUV and X-ray energies.

The Marshall Grazing Incidence X-ray Spectrometer (MaGIXS: Champey et al. 2022) is primarily designed for diagnostics of the coronal heating frequency for ARs (see Section 2). MaGIXS is a sounding rocket mission whose first successful flight was carried out on 2021 July 30. In this work, we study the heating frequency of an XBP that MaGIXS observed.

We have derived the loop structures of the XBP using the linear force-free (LFF) extrapolation of the photospheric line-of-sight (LOS) magnetogram observed by the Helioseismic and Magnetic Imager (HMI: Scherrer et al. 2012) on board SDO. The emission of these XBP loops is simulated using the HYDrodynamics and RADiation (HYDRAD) ¹²  code (Bradshaw & Mason 2003; Bradshaw & Cargill 2013; Bradshaw 2024) for nanoflare heating, whose frequencies and magnitudes are estimated from the loop parameters (e.g., lengths and magnetic field strengths). Here, we consider that nanoflares originated from the dissipation of magnetic energy stored within the loop. From the simulated outputs, we calculate the EM distributions and generate synthetic images of the XBP. These synthetic images are compared with the MaGIXS observation as well as the nearest available EUV and X-ray images observed by SDO/AIA and the X-Ray Telescope (XRT: Golub et al. 2007) on board Hinode (Kosugi et al. 2007).

Our goal here is to study whether nanoflare heating can explain the observed emission properties of the XBP and to investigate the importance of the MaGIXS, AIA, and XRT observations in determining the frequency of nanoflare heating. The rest of the paper is organized as follows. Section 2 describes the MaGIXS, AIA, XRT, and HMI observations of the XBP. Section 3 describes the simulation setup. The results are shown and discussed in Section 4, and Section 5 provides a brief summary of the work.

MaGIXS is a grazing incidence widefield slot imaging spectrometer, consisting of a Wolter-I telescope, a slot, a grating spectrometer, a CCD camera, and a slit-jaw context imager. Its field of view (FOV) is restricted by the slot that is 12' wide and 33' long (Champey et al. 2022). The unique design of MaGIXS is optimized to capture a spectral and spatial overlappogram of a solar AR in the soft X-ray wavelength range from ∼8 to 30 Å(0.4–1.5 keV). Spectral measurements in this energy range are well suited to diagnosing the heating of ARs (Athiray et al. 2019). The first successful rocket flight of MaGIXS on 2021 July 30 at 18:20 UT was targeted to observe two ARs (12846 and 12849) in the northern and southern solar hemispheres. However, due to the internal vignetting, the effective FOV observed was 92 × 25' on the solar disk, sampling two XBPs (XBP-1 and XBP-2) and a portion of the AR (AR 12849; see Savage et al. 2023 for the details of the MaGIXS observation). It recorded 296 s of imaging spectroscopic observations with a cadence of 2 s. For this analysis, we utilized MaGIXS Level 2 data products, which are spectrally pure images of the XBPs (see Table 3 of Savage et al. 2023 and the text for a description of the data processing).

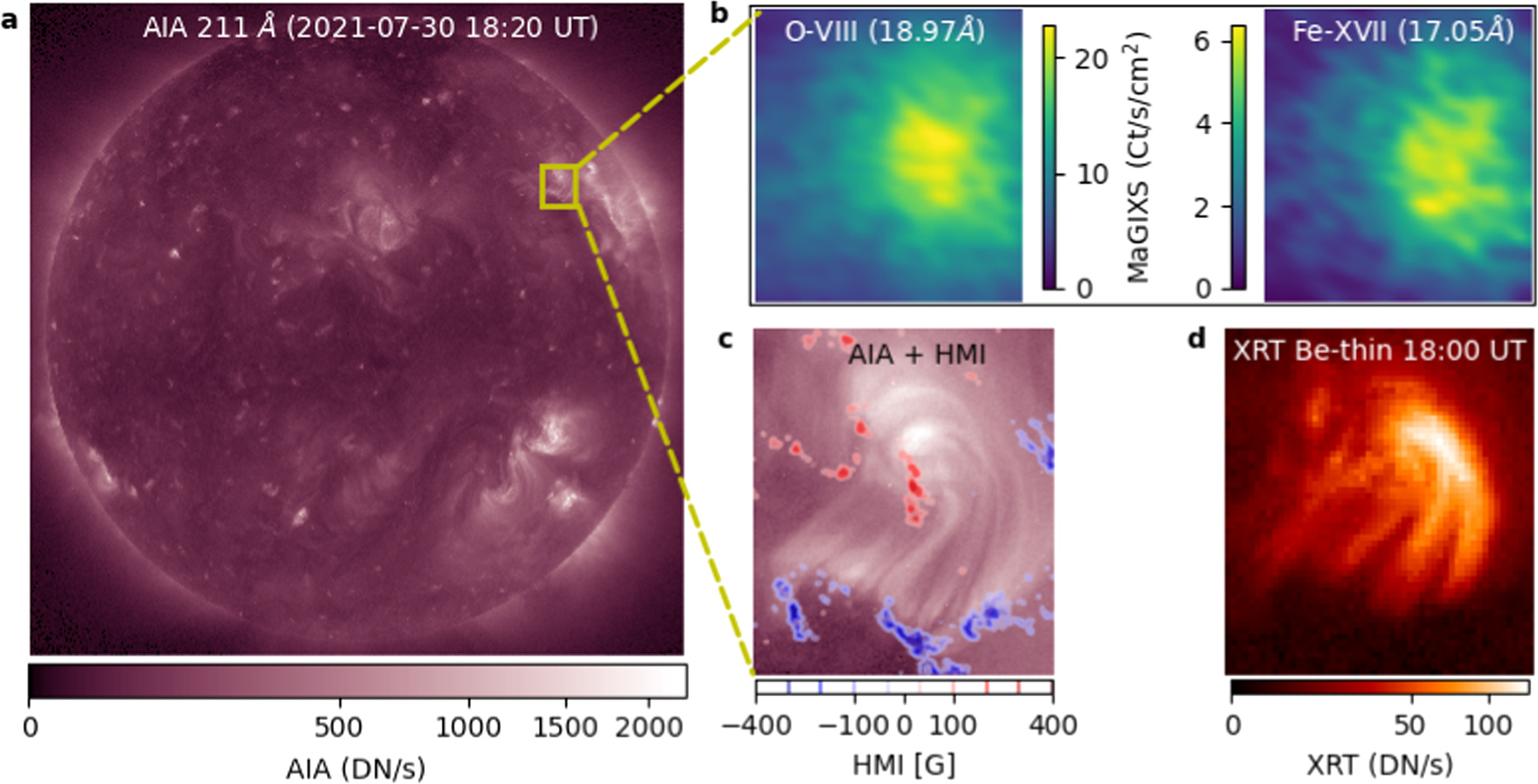
In the present study, we have concentrated on the study of XBP-1, to understand its heating frequency by comparing the observations with the simulated emissions from the hydrodynamic model. The location of XBP-1 on the full-disk image taken by the AIA/SDO 211 Å passband is shown in Figure 1(a) (yellow box). Figure 1(b) shows the spectrally pure maps of O viii and Fe xvii at 18.97 Å and 17.05 Å, derived from the MaGIXS observations as described in Savage et al. (2023). Each pixel of these images has a plate scale of 28 × 28, where, as in Savage et al. (2023), the spectrally pure maps are shown with a plate scale of 84 × 28. Along with MaGIXS, we have used the concurrent observations of this XBP in the EUV wavelength as observed by AIA/SDO. The Level 1 AIA data were downloaded from the Joint Science Operations Center and processed to Level 1.5 using the standard procedure in SunPy (The SunPy Community et al. 2020; Mumford et al. 2022). We also used the synoptic X-ray images for this XBP observed by Hinode/XRT at the closest available time to the MaGIXS observation, which was 20 minutes before. Panels (c) and (d) show the zoomed-in view of XBP-1 observed by the AIA 211 Å and XRT Be thin passbands, respectively. The red and blue contours in panel (c) represent the positive and negative polarities of the LOS photospheric magnetogram observed by SDO/HMI. To model the XBP-1 emission, we need to know the coronal loop structures associated with this XBP. For this, we have extrapolated the observed photospheric magnetogram, as described in Section 3.1.

Zoom In Zoom Out Reset image size

XBP-1 is associated with the bipolar magnetic field region and consists of loop structures, as visible in the EUV and X-ray images of AIA and XRT. Most of the X-ray emission is associated with these looplike structures. Field-aligned hydrodynamic simulations are often used to simulate the emission of the plasma confined within these loops. Here we have modeled the X-ray and EUV emission of the XBP-1 loops using the HYDRAD code. The HYDRAD code is described in detail in Bradshaw & Mason (2003) and Bradshaw & Cargill (2013). By accounting for the field-aligned gravitational acceleration and taking into account the bulk transport, thermal conduction, viscous interactions, gravitational energy, Coulomb collisions, and optically thick radiation in the lower atmosphere transitioning to optically thin radiation in the overlying atmosphere, HYDRAD is able to solve the time-dependent equations for the evolution of mass, energy, and momentum for multifluid plasma (electrons and ions) in a given magnetic geometry. HYDRAD can simulate the plasma response along the field-aligned direction for a given input heating profile and return the time evolution of temperature and density as a function of loop length. Here we employ the multispecies approach of HYDRAD, where electrons and ions are treated as separate fluids. Also we consider the plasma to be in equilibrium ionization and the loops to have a constant cross section.

We have derived the loop structures associated with XBP-1 from the LFF extrapolation of the high-resolution full-disk photospheric magnetograms observed by HMI/SDO, as discussed in Section 3.1. These loops are simulated with HYDRAD using heating profiles that depend on the length and field strength, as described in Section 3.2.

3.1. Magnetic Field Model

Using the locations of XBP-1, we have identified its counterpart on the full-disk LOS HMI magnetogram, which is associated with a bipolar region. Considering these bipoles as a lower boundary, we can extrapolate the field lines up to a height. However, as this region is located away from the disk center at a solar latitude and longitude of ∼50° and 30°, respectively, the extrapolated loops might have a significant projection effect on the disk plane. Thus, using the reproject_to functionality of the SunPy Map object, we have reprojected the HMI magnetogram to an observer LOS at 50° latitude and 30° longitude. Figure 2(a) shows the reprojected magnetogram. From this magnetogram, we have extrapolated the field lines up to a height of 500 HMI pixels (∼180 Mm). For this purpose, we have used the LFF extrapolation code, j_b_lff.pro (Nakagawa & Raadu 1972; Seehafer 1978), available within the SolarSoftWare (SSW) package (Freeland & Handy 1998). Using the three-dimensional extrapolated magnetic field data, we have traced field lines through the volume corresponding to XBP-1 following the streamline tracing method. For the streamline tracing, we have chosen the seed points (through which the field lines pass) randomly within the region of XBP-1 where the absolute field strength is more than 20 G at the base. A force-free parameter, α = −0.05 in our LLF model, provides a better match of the extrapolated loops with the observed emission in the AIA passbands. We have traced 300 loops, which is sufficient to represent the ensemble of the whole XBP-1 region in visual inspections. Projections of the extrapolated field lines onto the magnetogram are shown in Figure 2(b). Note that these field lines are projected with respect to a different observer LOS than those of the AIA and XRT images shown in Figure 1. Thus, to compare with the morphology of the observed AIA and XRT images, we have re-oriented the 3D extrapolated loops toward the Sun–Earth LOS by rotating them with same latitude (50°) and longitude (30°) and then taking a projection, as shown in Figure 2(c). The loop morphology now closely matches the AIA and XRT images. Figures 2(d) and (e) show the distribution of all the extrapolated loop lengths and the length-averaged magnetic field (〈B〉) distribution (see Equations (3) and (4) of Mondal et al. 2023 for details). The loop length distribution has a peak near 100 Mm and the average magnetic field is found to vary inversely with loop length, similar to an AR, as obtained by Mandrini et al. (2000). The 〈B〉 ∝ L⁻¹ relation is overplotted by a black line in Figure 2(e) as a reference.

Zoom In Zoom Out Reset image size

3.2. Heating Profile

To simulate the coronal loops, we assume the loops are in hydrostatic equilibrium at the beginning (t = 0 s), by setting boundary conditions for the footpoints' temperature and density. Once we provide the boundary values, HYDRAD calculates the initial temperature and density profiles along the loops. We have chosen a footpoint temperature of 20,000 K, as it seems reasonable to consider an isothermal chromosphere in the absence of any detailed knowledge (Bradshaw & Mason 2003). The footpoint density is chosen such that the coronal loop average temperature remains at a value close to 0.5 MK (see the Appendix for details), which is a reasonable lower boundary condition in the absence of any external heating.

We consider that the loops are continuously heated by nanoflares (Parker 1988; Klimchuk 2015), which can occur with the release of stored magnetic energy that derives from slow photospheric driving. To derive the energy and occurrence frequency of these nanoflares, we employ the approach of Mondal et al. (2023). Here we will briefly describe it.

We define the nanoflare heating in terms of a series of symmetric triangular profiles having a duration (τ) of 100 s, similar to previous studies (e.g., Klimchuk et al. 2008; Cargill et al. 2012b; Barnes et al. 2016). The peak heating rate of a nanoflare is randomly chosen between the minimum (H₀ ^min) and maximum (H₀ ^max) values associated with a loop. The maximum energy density is considered to be equal to the stored magnetic energy, due to the misalignment of the loop from vertical. If θ is the tilt of the magnetic field from vertical, then the H₀ ^max associated with the ith loop would be

$$\begin{eqnarray}&&{H}_{{0}_{i}}^{\max }=\displaystyle \frac{1}{\tau }\displaystyle \frac{{\left(\tan (\theta )\langle B{\rangle }_{i}\right)}^{2}}{8\pi }(\mathrm{erg}\,{\mathrm{cm}}^{-3}\,{{\rm{s}}}^{-1}).\end{eqnarray} \tag{ 1 }$$

We consider H^min ₀ as 1% of H^max ₀. Here, θ is known as the Parker angle and it has been found that to satisfy the observed coronal heating energy requirement, the value of $\tan (\theta )=c$ should be in the range of 0.2–0.3 (Parker 1988; Klimchuk 2015).

Because the free energy associated with a stressed loop is released during an impulsive event, releasing larger energy naturally creates a longer delay in accumulating enough energy to be released by the following event. Taking this key consequence, we assume that the delay time between two successive events is proportional to the energy of the first event. The delay time between the (l − 1)th and lth event will be

$$\begin{eqnarray}&&{d}_{i}^{l}=\displaystyle \frac{\tau L}{{F}_{i}}\times {H}_{i}^{l-1}.\end{eqnarray} \tag{ 2 }$$

Here, F_i is the Poynting flux associated with the ith loop by the photospheric driver.

Mondal et al. (2023) estimated F by two different methods. In the first method, they assumed that all the loops associated with all the XBPs have the same average Poynting flux, which is calculated from the observed differential emission measure (DEM), and in the second method, they considered a different Poynting flux for each loop derived from the expression of the Poynting flux by the photospheric driver (Klimchuk 2006). Here we have used the modified expression for the Poynting flux, considering the scenario of expanding loops with coronal height (Mondal et al. 2023):

$$\begin{eqnarray}&&F=-\displaystyle \frac{1}{4\pi }{V}_{h}\tan (\theta ){B}^{\mathrm{base}}\langle B\rangle .\end{eqnarray} \tag{ 3 }$$

Here, V_h is the horizontal speed of the flow that drives the field, 〈B〉 is the average field strength along the loop, and B^base is the magnetic field at the coronal base. Figure 3 shows the estimated heating profiles for three loops taken from the extrapolated distribution, as shown in Figure 2. Figures 3(a) and (b) show the heating profiles associated with V_h = 1.5 km s⁻¹ and V_h = 0.5 km s⁻¹, respectively, with a similar value of c = 0.2. Loops with a longer length and lower magnetic field strength produce more HF nanoflares compared with the loops with a shorter length and higher magnetic field strength.

Zoom In Zoom Out Reset image size

3.3. Simulation Runs and Outputs

Once we get the loop lengths and heating profiles for all the loops, we run the HYDRAD code for individual loops in a parallel computing environment using the Pydrad ¹³ (Barnes et al. 2023) interface. For each loop, we consider 5 Mm as the chromospheric height from each loop's footpoints. The location of each nanoflare event within a loop is determined from the Poisson probability by considering the expected location at the loop top with a significantly larger scale length (which determines how the heat will spread along the loop) in order to prevent localized heating. We simulate the evolution of the loops for a duration of 10,000 s and store the evolution of temperature and density for spatial grids of width 0.3 Mm (similar to HMI resolution) at a cadence of 25 s. Using these temperatures and densities for the last 1000 s of evolution, we calculate the time-averaged DEM for each grid point by considering an LOS plasma depth equal to the grid spacing (dl) along the loops. Note that assuming an LOS plasma depth equal to the grid spacing is a correct assumption for the dl almost parallel to the observer LOS, but this may not be appropriate for the portions of the loops, mostly at higher height, where dl is almost perpendicular to the observer LOS. Here, we use an LOS depth of ∼0.3 Mm (= dl) for the DEM calculation. According to the Hi-C observations (e.g., Peter et al. 2013), the smallest loops can have a diameter of 0.2 Mm, while the larger one could be 1.5 Mm. Thus, depending on the actual loop diameter, the loop-top emission might be slightly overpredicted/underpredicted. However, due to the lesser plasma density at the loop top, this would not affect the average DEM (∝ n² dl) significantly. We create the DEM in the temperature range of logT = 5.6–logT = 7.0 with δ(logT) = 0.1.

Using the DEM values and the projected coordinates of the loop grids (Section 3.1) on the HMI magnetogram, we have created DEM maps for all the loops associated with XBP-1. Folding this DEM map with the temperature response functions of the different passbands of AIA, XRT, and MaGIXS, we generate synthetic images of XBP-1 associated with each passband for the observation exposure time. Also, we apply Poisson statistics to the pixel counts. The AIA and XRT temperature responses (R_i ) are generated using the standard routine available in the SSW package, by applying passband degradation correction at the time of the observation. As our DEM maps are at the resolution of the HMI plate scales, the obtained R_i for AIA and XRT are converted to HMI plate scale. Also, we have applied a cross-calibration factor of 2 for XRT responses, as suggested by earlier studies (Schmelz et al. 2015; Wright et al. 2017; Athiray et al. 2020). The temperature responses of the different ions observed by MaGIXS are generated by multiplying the estimated contribution functions from CHIANTI (Dere et al. 1997; Del Zanna et al. 2021) with the MaGIXS effective area. For all the instruments, we have used coronal abundances (Feldman 1992).

As the simulated DEM maps are at HMI resolution, the synthetic images have the same HMI resolution of 05. To compare the synthetic images with the observation, they are rebinned with the instrument plate scale and then convolved with the instrument point-spread function (PSF). Plate scales of 06, 2'', and 28 are used for AIA, XRT, and MaGIXS. We used the scipy.ndimage.gaussian_filter (Virtanen et al. 2020) method for Gaussian PSFs with FWHMs of 12 for AIA, 2'' for XRT, and 30'' for MaGIXS (similar to the actual PSFs).

We repeat the simulation and create synthetic images for different heating parameters (c and V_h ) that determine the heating profile. Depending on the observation and the coronal energy losses, the values of V_h and c are chosen in the range of 0.5–2.0 km s⁻¹ and 0.2–0.3 (Klimchuk 2015). Figure 4(a) shows composite distributions of the peak heating rates of nanoflares for all the loops associated with different combinations of heating parameters. All the combinations of the heating rate frequency naturally follow a power law with the heating rate. Figure 4(b) shows distributions of the delay time between successive heating events for all the combinations of heating parameters. Combining Equations (1), (2), and (3), the delay time is proportional to c and inversely proportional to V_h . Thus, in Figure 4(b), increasing c represents more LF events (larger delay time) compared to HF events. On the other hand, increasing V_h results in more HF events (lower delay time) compared to LF events. Changing the heating parameters will change the Poynting flux associated with the loops, which determines the effective heating. The distributions of the average Poynting flux associated with all the loops are shown in Figure 4(c). The Poynting flux is proportional to V_h and c (Equation 3), causing an increase in flux with the increase of either V_h or c.

Zoom In Zoom Out Reset image size

In this study, we have performed hydrodynamic simulations of an XBP, observed by MaGIXS, to understand the nanoflare heating properties to maintain the heating of the XBP to the coronal temperature (>1 MK). Simulations are run for different combinations of heating parameters, and for each of them, the AIA, MaGIXS, and XRT images are synthesized as described in Section 3.3. The spatially averaged intensities at the different passbands of MaGIXS, AIA, and XRT are then compared with the average observed intensity. The top panel of Figure 5 shows the comparison of all combinations of heating parameters as a function of instrument passbands plotted on the abscissa. The black solid line represents the observed intensities, whereas the colored circles represent the synthetic intensities associated with the different heating parameters. The absolute values of synthetic intensity could deviate from the observed intensity due to various factors, e.g., the choice of the number of loops associated with the XBP, but the intensities should be off by a consistent ratio for all the passbands. Thus our intention is not to compare the absolute values of the observed and predicted intensities; rather, we compare the ratios between the predicted and the observed intensities for all the passbands. The ratio of predicted to observed intensities is shown in the bottom panel of Figure 5.

Zoom In Zoom Out Reset image size

We expect a similar ratio for all the passbands for a set of heating parameters that can explain the observation. To quantify how these ratios deviate from each other for a set of heating parameters, we derived the standard deviation (σ) from their mean value. A smaller value of σ indicates less deviation of the ratios from their mean and vice versa. The comparison of σ for the different instrument passbands as discussed above would be more appropriate if the cross-calibration factors among the instruments were well known, but these are currently limited and are being planned for the upcoming MaGIXS-2 flight (Athiray & Winebarger 2024). Therefore, here we compare the σ for different instruments separately. Figure 6 shows the σ values for MaGIXS, AIA, and XRT. The Y-axis represents σ and the X-axis shows the heating parameters. We found that σ is converging (gray shaded region) toward a minimum value for both XRT and MaGIXS, indicating a better match between the predicted and observed intensities, whereas for AIA, σ is less variable for the different heating parameters, indicating that using only the AIA passbands provides less sensitivity to determining the heating parameters and hence the heating frequency. In the present study, most of the AIA passbands are sensitive to the cool/warm (around or below 1 MK) plasma, which is the reason for the AIA passbands being less sensitive to the heating parameters, as discussed later in this section.

Zoom In Zoom Out Reset image size

Table 1 summarizes the values of the heating parameters for which both MaGIXS and XRT show converging σ. The range of the average Poynting flux associated with converging σ is 3.0 × 10⁵ erg cm⁻² s⁻¹ to 4.0 × 10⁵ erg cm⁻² s⁻¹, which is similar to the average Poynting flux of coronal XBPs derived by Mondal et al. (2023) during the minimum of solar cycle 24. This Poynting flux is more than 1 order of magnitude smaller than that of ARs (∼10⁷ erg cm⁻² s⁻¹), as predicted by Withbroe & Noyes (1977), which is expected, considering the less magnetic activity of the XBPs.

Table 1. Heating Parameters That Explain the Observations

c = $\tan (\theta )$	Vh	Average Delay	Average Flux
	(km s–1)	(s)	(105 erg cm−2 s−1)
0.25	1.0	2700	3.0
0.20	1.5	1600	3.8
0.30	1.0	2900	4.1

Download table as:  ASCIITypeset image

The average delay times between the nanoflares are in the range of 1500–3000 s. This time range is smaller than the average cooling times (on the order of 10⁴ s) of the loops according to the formula given by Cargill (2014), assuming similar equation parameters as those used by Barnes et al. (2021). This suggests that the heating is dominated by HF nanoflares, which is further supported by the fact that MaGIXS did not observe very hot (>5 MK) plasma for this XBP (Savage et al. 2023).

Figure 7 shows the representative comparison of the observed and simulated images for the heating parameters, c = 0.2 and V_h = 1.5 km s^–1, in different passbands of AIA, MaGIXS, and XRT. As we are not comparing the absolute intensities, the images are normalized with their maximum pixel values.

Zoom In Zoom Out Reset image size

The overall emission morphology of the XBP in the synthetic AIA images closely matches the observed images, except in a few places, such as the bright, cool (approximately 1 MK) structure in the bottom right of the observed 171 Å and 131 Å passbands. A closer inspection of this bright structure reveals its association with different sets of coronal loops that are not present in our magnetic model. Also, the observed images have diffuse background emissions, which are not present in our magnetic model and hence in the simulated emission. Due to the poor spatial resolution of MaGIXS, the loop structure of the XBP is not present in either the observed or predicted images, but they show brightening at similar locations. However, the synthetic O xiii image shows a slightly more elongated brightening in the y-direction than in the observed one. The emission morphologies in the XRT synthetic images are slightly different than the observed emission. We think this might be due to the fact that the XRT observed images are 20 minutes earlier than the synthetic images, and at that time the magnetic field morphology was slightly different. In addition, we observed that the synthetic image in the MaGIXS Fe xviii passband does not predict a significant emission indicating the absence of hot (>5 MK) plasma, which is consistent with the observations, as discussed by Savage et al. (2023). Also, the synthetic EM-weighted temperature of the XBP for c = 0.2 and V_h = 1.5 km s⁻¹ is found to be around 2 MK, which is similar to the predicted temperature from the MaGIXS observations.

Figure 8 showcases how the emission morphology varies with the heating parameters in the XRT Be thin filter. It is clearly visible that the synthetic emission morphology in the XRT Be thin filter is strongly dependent on the heating parameters, and we found similar results for the passbands sensitive to high temperature. This means that the heating parameters are very sensitive to matching the high-temperature emission. A similar conclusion can be drawn by looking into the ratios of the spatially averaged synthetic and observed intensities, as shown in the bottom panel of Figure 5. The ratios associated with different heating parameters show larger spreads for the passbands that exhibit high-temperature sensitivity. For instance, Fe xvii and Ne ix, whose peak emissivity temperatures (T_max) occur at log T = 6.75 and 6.6, show large spreads (∼0.5–6) in ratios; O viii, with T_max at log T = 6.5, exhibits a lesser spread (∼0.5–2.5) in ratios; and the cooler MaGIXS passbands O vii and N vii, with T_max at log T = 6.3, clearly show ratios varying < 2. A similar trend is also clearly observed with the AIA passbands. Having lesser sensitivity of the hot plasma in the AIA passbands, they show a lesser variation in the intensity ratios.

Zoom In Zoom Out Reset image size

In this study, we have established a methodology to study the nanoflare heating frequency in coronal structures. This would be useful for studying the capabilities and requirements of the upcoming instruments to diagnose the heating frequency. In the upcoming flight of MaGIXS, if it observes the hot (>5 MK) ARs, where LF events are expected to occur, a similar analysis would be very useful to separate the contribution of HF and LF nanoflares for coronal heating budgets.

Our formulation of the nanoflare heating profile in the present study is based on the dissipation of magnetic energy. In future, a similar methodology could be useful for studying the contribution of wave heating, by adopting the wave-heating scenario in the model, such as described by Reep et al. (2018).

We have studied the nanoflare heating frequency of an XBP observed during the the first successful flight of MaGIXS, along with the nearest available observations from SDO/AIA and Hinode/XRT. We compared the observed emission of this XBP with the simulated emission. The 1D hydrodynamic simulation code HYDRAD is used to simulate the XBP loops. The geometric properties of the loops are derived from the LFF field extrapolation of the observed photospheric magnetogram by SDO/HMI. The loops are assumed to be heated by random nanoflare events, depending on their length and magnetic field strength. The simulated emission in all instruments closely matches the nanoflare heating model, with the average Poynting flux in the range of 3.0 × 10⁵ to 4.0 × 10⁵ erg cm⁻² s⁻¹. The average delay time between the nanoflares is found to be 1500–3000 s, which is likely smaller than the average cooling time of the loops, suggesting the heating is dominated by HF nanoflares. Also, we have investigated the sensitivity of the MaGIXS, XRT, and AIA passbands to diagnosing nanoflare frequency. We found that in our method, where we compare the average intensities of the observed and synthetic images, the XRT and MaGIXS passbands are sensitive enough to diagnose the average nanoflare heating frequency, whereas AIA is the least sensitive.

We acknowledge the Marshall Grazing Incidence X-ray Spectrometer (MaGIXS) instrument team for making the data available through the 2014 NASA Heliophysics Technology and Instrument Development for Science (HTIDS) Low Cost Access to Space (LCAS) program, funded via grant NNM15AA15C. MSFC/NASA led the mission, with partners including the Smithsonian Astrophysical Observatory, the University of Central Lancashire, and the Massachusetts Institute of Technology. MaGIXS was launched from the White Sands Missile Range on 2021 July 30. The research of B.M. was supported by an appointment to the NASA Postdoctoral Program at the NASA Marshall Space Flight Center, administered by Oak Ridge Associated Universities, under contract with NASA. G.D.Z. and H.E.M. acknowledge the support of STFC. P.T. was supported on this work by NASA contract NNM07AB07C (Hinode/XRT) to the Smithsonian Astrophysical Observatory. We also acknowledge the helpful comments from an anonymous reviewer.

Facility: SDO (AIA, HMI) - Solar Dynamics Observatory, Hinode (XRT) - Hinode (Solar-B), MaGIXS -

Software: Astropy (Astropy Collaboration et al. 2018), IPython (Perez & Granger 2007), matplotlib (Hunter 2007), NumPy (Harris et al. 2020), scipy (Virtanen et al. 2020), SunPy (The SunPy Community et al. 2020), SolarSoftware (Freeland & Handy 1998).

The initial conditions are the initial temperature and density profiles along the loop length at t = 0 s, which HYDRAD evolves with time, subject to some external driver. More information on configuring the initial conditions can be found in the HYDRAD user manual. ¹⁴ At the beginning, we consider the loops to be in hydrostatic equilibrium, which ensures that at later time (t > 0 s) the evolution is only due to the external driver. Taking into account a few simplified assumptions in hydrostatic equilibrium (see Equation (9) in Reale 2010), we can write

$$\begin{eqnarray}&&P\approx \displaystyle \frac{1}{L}{\left(\displaystyle \frac{{T}_{\max }}{1.4\times {10}^{3}}\right)}^{3}.\end{eqnarray} \tag{ A1 }$$

Here, P is the uniform pressure throughout the loop of length L and T_max is the maximum temperature.

We want to keep the loop (above the chromosphere) with an average temperature (T_avg), e.g., 0.5 MK, which is a reasonably lower value. Following Cargill et al. (2012a), we can write

$$\begin{eqnarray}&&{T}_{\mathrm{avg}}\approx 0.9\times {T}_{\max }.\end{eqnarray} \tag{ A2 }$$

Also, from the ideal gas law,

$$\begin{eqnarray}&&P={nkT}.\end{eqnarray} \tag{ A3 }$$

Combining Equations (A1)–(A3), the footpoint density would be

$$\begin{eqnarray}&&{n}_{\mathrm{base}}=\displaystyle \frac{{P}_{\mathrm{base}}}{{{kT}}_{\mathrm{base}}}.\end{eqnarray} \tag{ A4 }$$

Following Bradshaw & Mason (2003), a footpoint temperature of 20,000 K is physically reasonable to treat a stratified, isothermal chromosphere (where the scale height is constant), in the absence of detailed knowledge and a thorough treatment. Note that the chromospheric density is important; if it is too low, then a very strong nanoflare could essentially ablate the entire mass content of the chromosphere into the corona, emptying it out and causing the transition region (basically, a thermal conduction front) to hit the edge of the computational domain, which is not desirable. A denser chromosphere can be obtained by choosing a lower isothermal temperature (e.g., 10,000 K instead of 20,000 K).

Consider L = 60 Mm. Then, from Equation (A4), to maintain an average temperature of 0.5 MK throughout the coronal portion of the loop, the footpoint density n_base ≈ 4 × 10⁹ cm⁻³. Once we know the footpoint density and temperature and provide them to HYDRAD, the code will calculate the initial temperature and density profile along the loop, as shown in Figure A1.

Zoom In Zoom Out Reset image size