Power Anisotropy, Dispersion Signature and Turbulence Diffusion Region in the 3D Wavenumber Domain of Space Plasma Turbulence

Plasma turbulence is ubiquitous in most space environments, including the solar wind (SW) (Alexandrova et al. 2013; Bruno & Carbone 2013) and the magnetosheath (Sahraoui et al. 2003; Huang et al. 2014; Sahraoui et al. 2020). Investigations of turbulence are necessary to understand the acceleration, heating, and transport of space plasmas (Schekochihin et al. 2009; Howes et al. 2011). Turbulence exhibits an anisotropic distribution of fluctuation energy in wavenumber ( k ) space, i.e., a (power) spectral anisotropy (Horbury et al. 2012; Oughton et al. 2015; Narita 2018). This kind of anisotropy is typically characterized by weaker and stronger power levels when sampled along the parallel and perpendicular directions relative to the background magnetic field, respectively. In earlier studies, the "Maltese-cross" pattern of the magnetic correlation function at 1 au shows that turbulence exhibits features of a "Slab+2D" configuration (Matthaeus et al. 1990), which consists of parallel waves and perpendicular structures. As an alternative, the Critical Balance (CB) theory proposed by Goldreich & Sridhar (1995) assumes that the magnitudes of the linear (e.g., Alfvén) timescale τ_A and of the nonlinear timescale τ_NL are comparable, leading to a balance between the effects of wave propagation and nonlinear interaction. Applying CB theory to Alfvén waves yields scaling indices of the power spectral density (PSD) of −2 in the parallel direction and −5/3 in the perpendicular direction, which are in agreement with the observed dependence of PSD indices on the sampling direction relative to the local background magnetic field (θ_VB) in single-point time series analyses of the the SW (Horbury et al. 2008).

The observation of the scaling anisotropy at magnetohydrodynamics (MHD) scales is to some degree sensitive to the determination of the background magnetic field direction. However, power anisotropy still exists throughout the inertial range (Wu et al. 2020). Anisotropy also exists in the kinetic range (Leamon et al. 1998; Sahraoui et al. 2010b). Involving appropriate kinetic wave modes in critically balanced cascade models permits the prediction of the scaling anisotropy at kinetic scales. Ideally, a critically balanced kinetic Alfvén wave (KAW) cascade would satisfy ${k}_{\parallel }\propto {k}_{\perp }^{1/3}$ (Cho & Lazarian 2004; Chen et al. 2010). Spectral anisotropy of turbulence is also found in the magnetosheath (Alexandrova et al. 2008; He et al. 2011c). A recent statistical survey conducted by Wang et al. (2020) has found a scale-dependent 3D anisotropy pattern of the structure function down to electron scales, with the relation ${l}_{\parallel }\propto {l}_{\perp }^{0.72}$ for the parallel and the perpendicular correlation lengths with respect to the local mean magnetic field (Chen et al. 2012). The observational scaling cannot be explained by the theory based on KAWs with CB, which predicts ${l}_{\parallel }\propto {l}_{\perp }^{1/3}$ (equivalent to ${k}_{\parallel }\propto {k}_{\perp }^{1/3}$), and calls for further investigation into intermittency and alternative turbulence mechanisms.

The scale-dependent statistics of the local-mean-field coordinate system can potentially interfere with the scale-dependent statistics of the fluctuations (e.g., second-order structure function). This complication could affect the interpretation of statistical results (Oughton & Matthaeus 2020). Therefore, we adopt the global mean magnetic field, and take the average over a short time interval to minimize the influence of the background field variation on the fluctuations themselves. The coexistence of different wave modes at kinetic scales complicates the study of small-scale plasma turbulence furthermore (He et al. 2011a, 2011b; Podesta 2012; He et al. 2015; Zhu et al. 2019).

Nevertheless, when dealing with data offered by only one spacecraft, as the spatial and temporal variations are entangled, it is impossible to define the full four-dimensional (4D) PSD directly. This problem is a key driver for multi-spacecraft missions like Cluster II (Escoubet et al. 2001) and the Magnetospheric Multiscale mission (MMS) (Burch et al. 2016), and advanced multi-spacecraft analysis techniques, including the k-filtering technique (also called the wave telescope technique) we apply in this work. It was proposed by Capon (1969), and introduced to space physics by Dunlop et al. (1988), Neubauer & Glassmeier (1990), and Pinçon & Lefeuvre (1991). As a generalized minimum variance analysis, it gives an estimation of the four-dimensional PSD(ω, k ) based on a Fourier transformation so that time variations and spatial variations are separated. Cluster II is the first mission that has offered applicable data sets for this technique (Glassmeier et al. 2001; Sahraoui et al. 2003). Sahraoui et al. (2006) investigated an event dominated by mirror-mode turbulence with strong power anisotropy, starting their investigation into turbulence with this technique.

Narita et al. (2010a) presented the first 4D PSD for measurements of the turbulent magnetic field, which paved the way for our methodology presented in this article. In this method, the smallest separation between the spacecraft defines the smallest scales of the turbulence that can be resolved. Besides the magnetic field, Cluster II also enables the study of multidimensional PSDs of plasma density (Roberts et al. 2017), and the possibility to study ion-velocity measurements, as was preliminarily discussed by Narita et al. (2010b). The MMS mission provides high-resolution data sets and smaller satellite separations down to the electron scale for this technique. Narita et al. (2016) presented a comprehensive case study of turbulence based on MMS observations, including the wave mode, dispersion relation, and propagating direction of waves. Besides the magnetic field, Narita et al. (2010b) also proposed that other measurements be used for multidimensional studies, and Roberts et al. (2019) were the first to apply k-filtering to the electron density data from Cluster II. However, k-filtering analyses of the turbulent fluctuation of electric field are rare. A series of inspiring works argued in favor of including the electric field in this type of study to acquire additional information about the polarization of the fluctuations (Tjulin et al. 2005, 2007, 2008). After Tjulin, however, we can hardly find any applications involving the electric field.

The fluctuating electric field and its PSD play important roles in plasma turbulence. According to Faraday's law, bifurcation of the PSDs of electric fluctuations and magnetic fluctuations is a signature of dispersion at kinetic scales, which was used by Bale et al. (2005) to support the notion that turbulence has a KAW nature at sub-ion scales. The electric field is often used, together with the current density, to estimate the energy-transfer rate between bulk flows and fields as J · E or ${\boldsymbol{J}}\cdot {\boldsymbol{E}}^{\prime}$, where ${\boldsymbol{E}}^{\prime}$ is the electric field in the ion-flow reference frame (Zenitani et al. 2011; He et al. 2019; Bandyopadhyay et al. 2020; Duan et al. 2020; Matthaeus 2021). Additionally, by computing ${\boldsymbol{E}}^{\prime} ={\boldsymbol{E}}+{{\boldsymbol{v}}}_{{\rm{i}}}\times {\boldsymbol{B}}$ and using $| \delta {\boldsymbol{E}}^{\prime} | /| \delta {\boldsymbol{E}}|$ as a metric, where δ E denotes the fluctuation of the electric field (Chen et al. 2011), it is possible to determine the plasma demagnetization in magnetic reconnection events (Hesse et al. 1999; Birn & Priest 2007; Lu et al. 2010). This metric has been adopted by Duan et al. (2018) for the computation of energy transfer in plasma waves based on linear kinetic theory to illustrate the diffusion of magnetic flux relative to the flow of plasma in wavenumber space, which becomes significant when approaching kinetic scales. He et al. (2020) further proposed the concept of turbulent ion and electron diffusion regions (T-IDR and T-EDR, respectively) based on the observed ratio $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{{\rm{i}}/{\rm{e}},\mathrm{local}}^{{\prime} })/\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{{\rm{i}},\mathrm{global}})$ as a reasonable alternative to $| \delta {\boldsymbol{E}}^{\prime} | /| \delta {\boldsymbol{E}}|$. In He et al. (2020), δ E _i,global is defined as δ E _i,global = E _sc + 〈 v _i〉 × B , where the subscript "sc" indicates the electric field is measured in the spacecraft frame and the angle brackets mean averaging over the whole interval. $\delta {{\boldsymbol{E}}}_{{\rm{i}}/{\rm{e}},\mathrm{local}}^{{\prime} }$ is defined as $\delta {{\boldsymbol{E}}}_{{\rm{i}}/{\rm{e}},\mathrm{local}}^{{\prime} }={{\boldsymbol{E}}}_{\mathrm{sc}}+{{\boldsymbol{v}}}_{{\rm{i}}/{\rm{e}}}\times {\boldsymbol{B}}$, where the subscript "i/e" means "ion/electron". In conclusion, the spectrum of the fluctuating electric field is related to basic features and mechanisms of plasma turbulence, especially at sub-ion scales. Reliable electric PSDs are necessary for investigations of this topic.

Based on the considerations above, we apply the k-filtering technique to a case study of plasma turbulence in the magnetosheath, using measurements from MMS. We compute PSDs from the high-resolution magnetic and electric field signals, i.e., PSD(δ B ( k )) and $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} }({\boldsymbol{k}}))$, respectively. We compare these two PSDs to attain the dispersion signature in 3D wavenumber space. We compute the PSD of the electric field in the local ion-flow frame, $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} })$, and in the global (averaged) ion-flow frame, $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} })$. By calculating the ratio $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} })/\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} })$, we identify the T-IDR in 3D wavenumber space. In Section 2, we introduce our data set and methodology. We present our PSDs of the magnetic and electric field fluctuations, and discuss the dispersion signature, in Section 3. The T-IDR is shown and discussed in Section 4. In Section 5, we present a summary and our conclusions.

2.1. The K-filtering Technique and the Doppler Effect

Here we briefly review the k-filtering technique (Paschmann & Schwartz 2000). We use the original form of the technique, which consists of three main steps. First we apply a Fourier transformation to the signals, and then combine the resulting Fourier images into a vector, A (ω, r _i ), e.g., when we choose the magnetic field signals:

$$\begin{eqnarray}&&{\boldsymbol{A}}(\omega ,{{\boldsymbol{r}}}_{i})=\left[\begin{array}{c}{A}_{x}(\omega ,{{\boldsymbol{r}}}_{i})\\ {A}_{y}(\omega ,{{\boldsymbol{r}}}_{i})\\ {A}_{z}(\omega ,{{\boldsymbol{r}}}_{i})\end{array}\right],\end{eqnarray} \tag{ 1 }$$

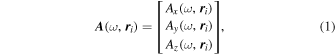
where the signal A can be a combination of vector components ( E , B or [ B , E ]^T ), or scalars (∣ B ∣, n, T, etc). Then we combine A (ω, r _i ) from the four different satellites together as ${[{\boldsymbol{A}}(\omega ,{{\boldsymbol{r}}}_{1}),{\boldsymbol{A}}(\omega ,{{\boldsymbol{r}}}_{2}),{\boldsymbol{A}}(\omega ,{{\boldsymbol{r}}}_{3}),{\boldsymbol{A}}(\omega ,{{\boldsymbol{r}}}_{4})]}^{T}$ (abbreviated as A (ω) with r _i omitted), and introduce the covariance matrix:

$$\begin{eqnarray}&&{{\mathsf{M}}}_{A}(\omega )=E\left[{\boldsymbol{A}}(\omega ){{\boldsymbol{A}}}^{\dagger }(\omega )\right],\end{eqnarray} \tag{ 2 }$$

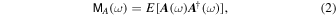
where E denotes the mathematical expectation and the dagger mark denotes the Hermitian conjugate. Assuming that the process is temporally ergodic, we approximate the expectation value as

$$\begin{eqnarray}&&{{\mathsf{M}}}_{A}(\omega )=\displaystyle \frac{1}{Q}\sum _{q=1}^{Q}{{\boldsymbol{A}}}^{q}(\omega ){{\boldsymbol{A}}}^{q\dagger }(\omega ),\end{eqnarray} \tag{ 3 }$$

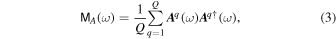
where Q is the number of the data segments (Paschmann & Schwartz 2000). These segments can overlap so that we apply a sliding window average. This kind of averaging reduces the presence of sporadic fluctuations (e.g., spikes) and thus reinforces the stationarity assumption assumed in the method (Motschmann et al. 1996; Tjulin et al. 2005). In our work, we set the length of every window as 2048 points and the sliding step as 512 points. We carry out an experiment by shifting the start point of the windows and find that the result stays relatively stable. To avoid inaccuracies due to the edge effect when applying the Fourier transform (Rezeau et al. 1999), we apply a Hamming window to every segment (Harris 1978). The matrix M _A needs to be guaranteed invertible (Tjulin et al. 2005). Therefore, we manually add noise, which is 0.1% of the wave amplitude at every frequency, to the diagonal elements of M _A .

We introduce the steering (wave-propagating) matrix H( k ), where I denotes the identity matrix:

$$\begin{eqnarray}&&{\mathsf{H}}({\boldsymbol{k}})=\left[\begin{array}{c}{\mathsf{I}}{{\rm{e}}}^{-{\rm{i}}{\boldsymbol{k}}\cdot {{\boldsymbol{r}}}_{1}}\\ {\mathsf{I}}{{\rm{e}}}^{-{\rm{i}}{\boldsymbol{k}}\cdot {{\boldsymbol{r}}}_{2}}\\ \vdots \\ {\mathsf{I}}{{\rm{e}}}^{-{\rm{i}}{\boldsymbol{k}}\cdot {{\boldsymbol{r}}}_{N}}\end{array}\right].\end{eqnarray} \tag{ 4 }$$

Using the Lagrange multiplier technique (Paschmann & Schwartz 2000), we obtain for the estimation of PSD the following expression:

$$\begin{eqnarray}&&\mathrm{PSD}(\omega ,{\boldsymbol{k}})=\mathrm{Tr}\left\{{\left[{{\mathsf{H}}}^{\dagger }({\boldsymbol{k}}){{\mathsf{M}}}_{A}^{-1}(\omega ){\mathsf{H}}({\boldsymbol{k}})\right]}^{-1}\right\}.\end{eqnarray} \tag{ 5 }$$

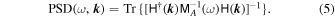
Previous studies remind us of several limitations of this technique (Sahraoui et al. 2010a). The technique is based on the assumption of weak stationarity of the turbulent fluctuations (Matthaeus & Goldstein 1982). Moreover, the geometric configuration of the spacecraft constellation determines the first Brillouin zone where the estimation is reliable. Due to the spatial aliasing effect, fluctuations separated by Δk = 2n π/d in k space cannot be distinguished. The maximum wavenumber k_max resolved in this technique is π/d, where d is the appropriate (averaged) separation of spacecraft in the constellation. This wavenumber k_max corresponds to a wavelength of λ = 2d. A configuration of the constellation close to a regular tetrahedron maximizes the Brillouin zone volume and reduces angular aliasing, which would otherwise create fake power anisotropy (Narita & Glassmeier 2009). Empirically given by Sahraoui et al. (2010a) to guarantee accurate positions of power peaks, the minimum resolved wavenumber k_min corresponds to ∼π/5d.

When estimating the PSD for magnetic fluctuations, it is necessary to add a divergence-free constraint, i.e., ∇ · B = 0 or its Fourier transformed form k · B = 0 (Motschmann et al. 1996; Tjulin et al. 2005). Applying this constraint requires the introduction of the matrix C(ω, k ), which is defined as

$$\begin{eqnarray}&&{\mathsf{C}}(\omega ,{\boldsymbol{k}})={\mathsf{I}}+\displaystyle \frac{{\boldsymbol{k}}{{\boldsymbol{k}}}^{\dagger }}{| {\boldsymbol{k}}{| }^{2}}.\end{eqnarray} \tag{ 6 }$$

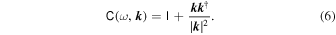
Then the PSD estimation is replaced by

$$\begin{eqnarray}&&{\mathrm{PSD}}_{{\boldsymbol{B}}}(\omega ,{\boldsymbol{k}})=\mathrm{Tr}\left\{{\left[{{\mathsf{C}}}^{\dagger }(\omega ,{\boldsymbol{k}}){{\mathsf{H}}}^{\dagger }({\boldsymbol{k}}){{\mathsf{M}}}_{A}^{-1}(\omega ){\mathsf{H}}({\boldsymbol{k}}){\mathsf{C}}(\omega ,{\boldsymbol{k}})\right]}^{-1}\right\}.\end{eqnarray} \tag{ 7 }$$

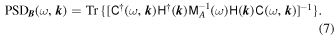
Due to the Doppler effect, there is a shift between the frequency of fluctuations measured in the spacecraft frame (ω_sc) and the frequency in the reference frame defined by the plasma flow (ω_pl). In order to compare with theoretical predictions and eliminate the Doppler shift, we reconstruct PSD(ω_pl, k ) from the direct result PSD(ω_sc, k ). Using the Doppler relation ω_pl = ω_sc − k · v , we map the value of PSD(ω_sc, k ) directly to the corresponding PSD(ω_pl, k ). In this work, we use the time-averaged ion bulk velocity V _0,i for the calculation of the Doppler shift. As the relation ω_pl = ω_sc − k · v corresponds to oblique planes in the 4D (ω_sc, k ) space if ω_pl is set, the reconstruction method can be symbolized like cutting 4D bread into slices with an oblique knife. In the computation, independent variables are discrete, so linear interpolation is employed here. When ω_pl is linked with negative ω_sc, we use the equality

$$\begin{eqnarray}&&{\rm{P}}{\rm{S}}{\rm{D}}({\omega },{\boldsymbol{k}})={\rm{P}}{\rm{S}}{\rm{D}}(-{\omega },-{\boldsymbol{k}}).\end{eqnarray} \tag{ 8 }$$

A visual description of this procedure is included in the Appendix.

It is beneficial to mention the multipoint signal resonator (MSR) technique (Choi et al. 1993; Narita et al. 2010b) and why we do not use it here. The MSR technique helps reduce noise in the wavevector analysis by multiplying a matrix that automatically adjusts the diagonal terms. However, the assumption of MSR that the data contain a finite number of wave signals and noise may not be satisfied when analyzing a turbulent event. The power index n in Equation (42) of Narita et al. (2010b) introduces the effect that the power ratio of two waves may alternate, which we want to avoid when comparing power spectra as in our work.

2.2. Data Set for Analysis

The observations analyzed are from MMS from 09:24:11 to 09:25:07 on 2015 October 16, when the satellites were located in the magnetosheath close to the dusk magnetopause, at a distance of 11.9 R_E from Earth. The same event has been reported by Chen & Boldyrev (2017) as an event with wavevector anisotropy and kinetic Alfvén nature in the sub-ion range, but we neglect the last 17 s because the background magnetic field B ₀ rotated by about 10° then. The magnetic field data come from the Fluxgate Magnetometer (FGM) instrument (Russell et al. 2016). The electric field is measured by the Spin-plane Double Probe instrument (SDP) (Lindqvist et al. 2016) and the Axial Double Probe instrument (ADP) (Ergun et al. 2016). The probe-to-probe distance of SDP is about ∼120 m, and the distance is ∼30 m for ADP, which are both much shorter than the length scale of the electric fluctuations of concern (Goodrich et al. 2018). The quality of the electric field data is also checked by private communication with the MMS electric field team. We use data from the Fast Plasma Investigation (FPI) instrument, which provides the density, bulk velocity, and temperature of the ions (Pollock et al. 2016). The time cadences of the magnetic field and electric field measurements are 128 Hz and 8192 Hz, respectively.

The time series of the event is shown in Figure 1, with all the variables in the geocentric Solar ecliptic (GSE) coordinate system. This system has the x-axis toward the Sun and the z-axis perpendicular to the plane of Earth's orbit around the Sun (pointing northward). Some key parameters are listed in Table 1. The Alfvén speed exceeds the average ion flow velocity, which potentially causes a violation of the assumptions underlying Taylor's hypothesis, although, the k-filtering techniques does not depend on Taylor's hypothesis. The fluctuation level of the ion bulk velocity is small, which would minimize the Doppler effect broadening (Narita 2014).

Zoom In Zoom Out Reset image size

Table 1. Key Parameters of the Event

Variable Name	Value
B0, magnitude of the background magnetic field	38.8 nT
V0,i, average ion velocity	187 km s−1
VA, Alfvén speed	229 km s−1
ni, number density of ions	14.9 cm−3
ne, number density of electrons	13.3 cm−3
Ti, temperature of ions	208 eV
Te, temperature of electrons	23 eV
βi, plasma beta of ions	0.86
βe, plasma beta of electrons	0.096
di, ion inertial length	59 km a
ρi, ion thermal gyroradius	54 km
davg, average separation of satellites	14.4 km

Note.

^a We distinguish two kinds of units: distance divided by angle (e.g., km/rad) and linear distance (e.g., km).

Download table as:  ASCIITypeset image

As the time cadences of the magnetic field, electric field, and ion-velocity measurements are different, we interpolate the ion-velocity data and subsample the electric data to the magnetic field epochs of one single spacecraft. The magnetic field measurements from the four MMS spacecraft are also selected to be on the same timeline. The sampling rate of the velocity gives f_max = 6.7 Hz, and f_min is set to be 0.48 Hz, because signals with frequencies lower than f_min correspond to scales that are too large for the k-filtering method.

We point out that the ion velocity has the lowest sampling frequency and a noise level that cannot be ignored (Gershman et al. 2018; Scudder 2020). As a result, some residual electric fluctuations are not compensated for by the convection electric field (− V _i × B ), which we use to calculate the electric fluctuations in the local ion-flow frame. To evaluate further if the measurements are appropriate for analysis, 1D PSDs of the measured magnetic, electric, and ion-velocity fluctuations are also presented in Figure 1 (panels (h) and (i)), with the frequency ranges marked out. Here f_di and f_ρi are defined as f_di = V_0,i/2π d_i and f_ρi = V_0,i/2π ρ_i, respectively. The factor of $\sin ({\theta }_{{BV}})$, where θ_BV denotes the angle between the background magnetic field and the bulk flow, is about 0.81 in our case, and is not included in the calculation of f_di and f_ρi, since its value does not affect much the positions of f_di and f_ρi in Figures 1(h) and (i). The power of the electric fluctuations is normalized by the Alfvén speed. The maximum frequency (f_max) is below the Nyquist frequencies of both the magnetic and electric field measurements.

The steep power spectrum of the ion-velocity fluctuations is consistent with the expectation of KAW fluctuations (e.g., Zhao et al. 2014). Compared with the electric and magnetic fields, the spectrum of ion-velocity fluctuations is smaller and steeper, which indicates that the associated convection electric field fluctuations at higher frequencies are low. The contribution of ion velocities to the fluctuations of the convective electric field becomes negligible with decreasing scale (He et al. 2020). It follows that the interpolation of the ion velocity to a higher frequency (beyond its Nyquist frequency) to compute the electric field spectra is justified. We further describe this issue with a quantitative estimation in Section 4. The timescale corresponding to the crossing of the constellation by the flow corresponds to 10 Hz, which also adds constraints to the resolved data in our analysis but is not of primary concern (Bandyopadhyay et al. 2018).

The analyzed time interval fulfills the conditions for the application of the k-filtering method. The satellites almost formed a regular tetrahedron with elongation = 0.09 and planarity = 0.17 (Robert et al. 1998). The average separation of the satellites, d_avg, sets a ${k}_{\max }\sim 0.21\,{\mathrm{km}}^{-1}$, consistent with ${k}_{\max }{d}_{{\rm{i}}}\sim 12$, ${k}_{\min }\sim 0.04\,{\mathrm{km}}^{-1}$, and ${k}_{\min }{d}_{{\rm{i}}}\sim 2.4$. According to Sahraoui et al. (2010a), the relative uncertainty of the wavevector Δk/k is less than 10% if we have a relative random error of satellite separation of 5%. The standard variation of the satellite separation d_ij within the time interval is generally 2% of d_ij , where i and j denote the two satellites. Therefore, we adopt the relative uncertainty of k, i.e., Δk/k, as less than 10%. We rotate the reference frame so that ${{\boldsymbol{B}}}_{0}\,={B}_{0}{\hat{e}}_{\parallel }$, and set ${\hat{e}}_{\perp 1}$ and ${\hat{e}}_{\perp 2}$ along x_GSE × B ₀ and ${{\boldsymbol{B}}}_{0}\times {\hat{e}}_{\perp 1}$, respectively. Figures 2(a)–(f) show the reduced 2D power spectra of the magnetic and the electric fields, marked as P _B (k_i , k_j ) and ${P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}({k}_{i},{k}_{j})$, where k_i and k_j are any two different wavenumber components of k_∥, k_⊥1, and k_⊥2. It is calculated by integrating the 4D PSD over ω_pl and the other component of k , for example:

$$\begin{eqnarray}&&P({k}_{\parallel },{k}_{\perp 1})=\iint \mathrm{PSD}({\omega }_{\mathrm{pl}},{\boldsymbol{k}}){\mathrm{dk}}_{\perp 2}{\rm{d}}{\omega }_{\mathrm{pl}}.\end{eqnarray} \tag{ 9 }$$

We note that ${k}_{\min }{d}_{{\rm{i}}}$ marks a region within the PSDs where the uncertainty of the method is too large (e.g., Sahraoui et al. 2010a). For completeness, we retain the results in these regions but indicate by a circle where the uncertainty of the method becomes too large. Similar regions are also present in Figure 3. In these panels, we find a spectral anisotropy in the wavenumber space for both the magnetic and electric fluctuations. To compare the anisotropy levels, we fix the space between adjacent contour levels in all these six contours. The magnetic spectrum is more elongated with more contour levels in the k _⊥ direction, suggesting that it is more anisotropic than the electric spectrum.

For a quantitative comparison of the anisotropy, we adopt the metric introduced by Shebalin et al. (1983):

$$\begin{eqnarray}&&{\theta }_{S}\equiv {\tan }^{-1}\sqrt{\displaystyle \frac{{\sum }_{{\boldsymbol{k}}}{k}_{\parallel }^{2}| S({\boldsymbol{k}}){| }^{2}}{{\sum }_{{\boldsymbol{k}}}({k}_{\perp 1}^{2}+{k}_{\perp 2}^{2})| S({\boldsymbol{k}}){| }^{2}}}.\end{eqnarray} \tag{ 10 }$$

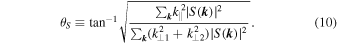
Here S( k ) is the spectral amplitude of a fluctuation in wavenumber space after the frequency integration of PSD(ω, k ), given as

$$\begin{eqnarray}&&| S({\boldsymbol{k}}){| }^{2}=\int \mathrm{PSD}({\omega }_{\mathrm{pl}},{\boldsymbol{k}}){\rm{d}}{\omega }_{\mathrm{pl}}.\end{eqnarray} \tag{ 11 }$$

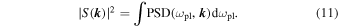
Only wavenumbers within $\left[{k}_{\min },{k}_{\max }\right]$ are included in Equation (10). By definition, small θ_S (approaching 0°) and large θ_S (approaching 90°) correspond to opposite anisotropies dominated by perpendicular and parallel wavevectors, respectively. We obtain θ _B = 25.3° and ${\theta }_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}=31.9^\circ$. We estimate the uncertainty of θ_S by applying the uncertainty propagation principle, i.e.:

$$\begin{eqnarray}&&{\varepsilon }_{f({x}_{1},{x}_{2},\ldots )}=\sqrt{\sum _{i}{\left(\displaystyle \frac{\partial f}{\partial {x}_{i}}{\varepsilon }_{{x}_{i}}\right)}^{2}},\end{eqnarray} \tag{ 12 }$$

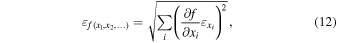
to Equation (10), where ε denotes the uncertainty of the subscript variable and f is a function of a set of x_i . According to Equation (10), we consider θ_S as fas a function of ∣S( k )∣² . In the calculation, we use Δk/k = 10% mentioned above as the initial uncertainty and estimate the uncertainty of ∣S( k )∣² empirically. We shift k by as much as 10% and check how much ∣S( k )∣² changes, which we find is always less than 30% of ∣S( k )∣², so we set the relative uncertainty of ∣S( k )∣² to 30%. Taking these together, we determine the relative uncertainty of θ_S as 5% for both the electric and the magnetic fluctuations, so that we confirm quantitatively a difference in the anisotropy levels.

Figure 2 shows the first 3D image of the bifurcation between PSD _B and ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$. Panels (a) and (d) give an indication of a non-axisymmetry in the power distribution, showing elongated power distributions. This pattern of P(k_⊥1, k_⊥2) reflects that in this event with a relatively short time interval, the kinetic waves have limited directions of k _⊥, which do not distribute evenly in the whole range of the azimuthal angle.

We compute the ${P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}/{P}_{{\boldsymbol{B}}}$ ratio and normalize it to the Alfvén speed, which is presented in Figures 2(g)–(i). The ratio is well below unity at small k (large scales), and increases to values greater than unity when ∣ k ∣ increases along the direction perpendicular to B ₀, where the fluctuation energy concentrates. The ratio increases even more steeply along the directions not perpendicular to B ₀. It exceeds 10 at ∣ k d_i∣ = 10 when k_∥ ≫ k_⊥.

Zoom In Zoom Out Reset image size

We further compute the ratio of $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} })$ to $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} })$ to measure the demagnetization and the diffusion of ions. These two PSDs are computed from the electric fields in the local ion-flow frame, ${{\boldsymbol{E}}}_{\mathrm{local}\ \ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} }={{\boldsymbol{E}}}_{\mathrm{sc}}+{{\boldsymbol{v}}}_{{\rm{i}}}\times {\boldsymbol{B}}$, and in the global ion-flow frame, ${{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} }={{\boldsymbol{E}}}_{\mathrm{sc}}+\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle \times {\boldsymbol{B}}$, where the angle brackets mean averaging over the whole interval.

As mentioned in Section 2, the fewer sampling points of the ion bulk velocity than the electric field and noise may affect the result of ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\mathrm{local}{{\boldsymbol{v}}}_{i}}^{{\prime} }}({\omega }_{\mathrm{pl}},{\boldsymbol{k}})$. In order to examine whether the measurement uncertainties have a significant effect on the power spectra, we conduct the following experiment. We generate random noise of the ion bulk velocity according to the measurement uncertainties given by the instrument team. Then, we add the noise to the time series of the ion bulk velocity and calculate the corresponding electric field ${{\boldsymbol{E}}}_{\mathrm{local}{{\boldsymbol{v}}}_{i}^{* }}^{{\prime} }$ in the local ion-flow frame with the modified ion velocity ${{\boldsymbol{v}}}_{{\rm{i}}}^{* }$. After that, we calculate ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\mathrm{local}{{\boldsymbol{v}}}_{i}^{* }}^{{\prime} }}({\omega }_{\mathrm{pl}},{\boldsymbol{k}})$ and compare it to ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\mathrm{local}{{\boldsymbol{v}}}_{i}}^{{\prime} }}({\omega }_{\mathrm{pl}},{\boldsymbol{k}})$. We find they are similar with only some slight differences, which do not affect the main features of the reconstructed PSDs. Therefore, we confirm that the fewer sampling points and the uncertainties of the ion bulk velocity measurement do not significantly affect the power spectra.

Figure 3 shows the ratio after appropriate integrations. We note here that the uncertainty of the PSD gradually grows with increasing wavenumber, and due to the division operation, the resulted ratios may have relatively large uncertainty at small scales so that they are less reliable. As the figure shows, the ratio is lower in regions close to quasi-perpendicular wavevectors than near quasi-parallel wavevectors. In panel (a), the region with a low ratio (less than 1) covers a large range of the parameter space. In panel (b), the low ratio range reaches k_⊥2 d_i > 5, and unlike the PSD, it is far less symmetric in k_⊥2.

Zoom In Zoom Out Reset image size

Using the New Hampshire Dispersion relation Solver (NHDS) (Verscharen & Chandran 2018) based on linear Vlasov–Maxwell theory, we calculate ratios of the fluctuations δ B , δ E , δ v _i, and δ v _e of the eigenmodes belonging to the Alfvén-mode branch under the same plasma conditions as measured (see Table 1). Figure 4 is derived from the output of NHDS. It is not easy to reach the very small scales and find the corresponding solutions based on NHDS, therefore we limit the wavenumber range to see the trend with respect to θ_kB. Figure 4(a) shows the modeled distribution of $| \delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} }| /| \delta {\boldsymbol{E}}|$ in wavenumber space in the plasma frame, which is considered equivalent to the square root of ${P}_{{{\boldsymbol{E}}}_{\mathrm{local}\,{{\boldsymbol{v}}}_{i}}^{{\prime} }}/{P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$. The ratio $| \delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} }| /| \delta {\boldsymbol{E}}|$ stays below 1.0 when k_∥ d_i < 0.5 and k_⊥ d_i < 1.0. It exceeds unity at smaller scales. A sharp edge near θ_kB = 30° is visible in panel (a), which separates the high and low ratios at small and large θ_kB, respectively. Another ridge-like boundary between the low and high ratios is also found at θ_kB = 70° when kd_i ≳ 2.5.

Figure 4(b) displays the normalized magnetic helicity σ_m . We also see an edge at θ_kB ∼ 30° in this panel corresponding to σ_m = 0. The normalized magnetic helicity σ_m is negative (positive) at θ_kB < 30° (θ_kB > 30°). The positive σ_m at large θ_kB is an evident feature of KAWs, which is distinguished from the negative σ_m at small θ_kB characteristic for ion cyclotron waves (ICWs).

Zoom In Zoom Out Reset image size

According to the linear-theory predictions in Figure 4(a), in the ICW regime, the metric of diffusion, ${P}_{{{\boldsymbol{E}}}_{\mathrm{local}{{\boldsymbol{v}}}_{i}}^{{\prime} }}/{P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$, exceeds 1.0 significantly. For ICWs at ion scales, the fluctuating electric field δ E can be approximated as −δ v _e × B ₀, since the electrons are still frozen-in with the magnetic fields. Therefore, the electric field in the local ion-flow frame can be approximated as $\delta {\boldsymbol{E}}^{\prime} \sim (-\delta {{\boldsymbol{v}}}_{{\rm{e}}}+\delta {{\boldsymbol{v}}}_{{\rm{i}}})\times {{\boldsymbol{B}}}_{0}$. On the other hand, we know that ∣δ v _i∣ > ∣δ v _e∣ and ∣δ v _i − δ v _e∣ > ∣δ v _e∣ for ICWs, which means that ions are the primary current carrier of the wave-current density, according to linear plasma wave theory. Therefore, we anticipate that $| \delta {\boldsymbol{E}}^{\prime} | \gt | \delta {\boldsymbol{E}}|$ for ICWs if they are indeed present. Comparing to this theoretical prediction, we observe that our k-filtering results do not show such a high ratio of the ion diffusion metric at quasi-parallel wavenumbers. This finding suggests that ICWs are not detectable in our measurement interval. Given the observed plasma conditions, ICWs are likely to be strongly damped at the wavenumbers we consider.

We employ another software package of plasma wave solver, Plasma Kinetics Unified Eigenmode Solution (PKUES) (He et al. 2021), which is modified and developed from the dispersion relation solver "Plasma Dispersion Relation Kinetics" (PDRK; Xie & Xiao 2016), to calculate the growth/damping rate of the ICW mode at larger wavenumbers under the observed plasma conditions and find the ICW mode has indeed a significantly increasing damping rate with increasing wavenumber. However, the diagnosis of the ICW damping process is beyond the scope of this work.

Figure 4(c) is the modeled distribution of ∣δ E ∣/∣δ B ∣, normalized to the Alfvén speed V_A. It can be compared with Figures 2(g)–(i). They are generally consistent at quasi-perpendicular wavevectors, but this similarity diminishes at small θ_kB where the theoretical distribution corresponding to ICWs does not find a counterpart in our k-filtering result. As the polarization (i.e., the imaginary part of the complex components) of the electric fields cannot be determined by k-filtering, we cannot tell exactly what the full wave-mode composition of our measurement interval is and cannot fully explain the distribution. It is possible that waves with a strong electrostatic component (e.g., quasi-parallel ion acoustic waves) may contribute to the corresponding power distribution. Due to the temporal aliasing in the frequency domain, electrostatic waves at smaller scales may also contribute to the electric spectrum (Graham et al. 2018), which is beyond the scope of our work. Nevertheless, our comparison of the dispersion properties measured by ∣δ E ∣/∣δ B ∣ reveals the dominant modes in our time interval as quasi-perpendicular KAWs.

For a case study of turbulence in the terrestrial magnetosheath, we compute the 4D PSDs of the turbulent magnetic and electric fields, recalculate the frequency in the plasma frame from its counterpart in the spacecraft frame, and reconstruct the PSDs with the frequency in the plasma frame. Both PSD _B and ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$ show typical anisotropy in the 2D (k_∥, k_⊥) plane, but ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$ is less anisotropic. We also find some degree of non-axisymmetry in the (k_⊥1, k_⊥2) plane, which agrees with Roberts et al. (2019). Such non-axisymmetry with elongation of the PSD may result from oblique KAWs at various k _⊥ being concentrated within a finite range of angles. The non-axisymmetry may also originate from a sampling effect (Turner et al. 2011, 2012). As discussed by Turner, the fact that only perturbations within $\left[-{\omega }_{\max },{\omega }_{\max }\right]$ can be detected by the spacecraft makes us miss wavevectors outside the frequency interval. As a consequence, the fluctuation component perpendicular to both B ₀ and V ₀ is weaker than the other component in the plane perpendicular to B ₀, according to the theoretical prediction for sampling an assumed axisymmetric distribution (Turner et al. 2011). However, it is still challenging to know whether there is, and the actual level of, non-axisymmetry.

We evaluate the bifurcation between PSD _B and ${\mathrm{PSD}}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{i}\rangle }^{{\prime} }}$ through $\displaystyle \frac{1}{{V}_{{\rm{A}}}^{2}}\displaystyle \frac{{P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} }}}{{P}_{{\boldsymbol{B}}}}$ usually considered as an indicator for dispersion in turbulence. We find in the quasi-perpendicular direction where the fluctuation energy concentrates, that the bifurcation agrees with the prediction for KAWs according to linear Vlasov–Maxwell theory. Apart from these features, the observation of $\displaystyle \frac{1}{{V}_{{\rm{A}}}^{2}}\displaystyle \frac{{P}_{{{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} }}}{{P}_{{\boldsymbol{B}}}}$ cannot be solely explained by the theoretical prediction based on the Alfvén wave branch alone.

For the first time, we compute the ratio between $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\mathrm{local}\ {{\boldsymbol{v}}}_{{\rm{i}}}}^{{\prime} })$ in the local ion bulk flow frame and $\mathrm{PSD}(\delta {{\boldsymbol{E}}}_{\langle {{\boldsymbol{v}}}_{{\rm{i}}}\rangle }^{{\prime} })$ in the global ion bulk flow frame. We compute the electric field power ratio to identify the ion demagnetization in wavenumber space at kinetic scales and compare it with the prediction of ion demagnetization in the Alfvén wave branch as calculated by NHDS. The ratio of the event exhibits anisotropy and asymmetry of wavevectors.

Considering the strengths of this method as described above, we anticipate that the k-filtering technique will become a powerful technique for the comprehensive investigation of diffusion physics in turbulence. Nevertheless, there are still open questions about the interval, e.g., the existence of other wave modes, the presence of intermittent structures like Alfvénic vortices (Wang et al. 2019; Chaston et al. 2020), or solitary waves (Alexandrova et al. 2006), for instance, the signal spike near 09:24:50. Although the k-filtering technique has shown considerable capability, it suffers from limitations and errors, as mentioned above. Especially spatial aliasing is a central issue, the challenge of which has been theoretically discussed by Narita & Glassmeier (2009). The spatial aliasing effect prevents us from quantifying the distribution of PSDs in (ω, k ) and quantitatively comparing the reduced PSDs with those obtained directly from Fourier/wavelet transformations of the time sequences. The limitation of this method to around (or even less than) one decade in wavevector space is another weakness of this technique, which prevents the simultaneous analysis of different plasma scales. A more flexible constellation with more than four satellites would be a prospect to be anticipated (Klein et al. 2019; Dai et al. 2020; Zhang et al. 2021).

The k-filtering technique also has the potential to study turbulence properties concerning phase spectra, e.g., magnetic helicity (Narita & Glassmeier 2009), although it needs effort and care to extract accurate phase information from the off-diagonal elements of M _A . We expect further application to studying the spectra of energy conversion rate using the fluctuations of the electric field and current density.

The authors are grateful to the teams of the MMS spacecraft for providing the data. The authors from China are supported by NSFC (41874200, 42174194, 42150105, and 42204166), by CNSA (D020301 and D050106), and by National Key R&D Program of China (2021YFA0718600). D.V. is supported by the STFC Ernest Rutherford Fellowship ST/P003826/1 and STFC Consolidated Grants ST/S000240/1 and ST/W001004/1. We sincerely thank Dr. Olga Alexandrova for the discussion with us at the vEGU meeting 2021. We sincerely thank Dr. Daniel Graham from the MMS electric field team for the confirmation of the availability of the electric field data.

Data availability: The original data is provided by NASA Coordinated Data Analysis Web (CDAWeb). For need of the analyzed data please contact the author.

We illustrate the effect of the Doppler shift in Figure 5, which imitates the presentation of Figure 9 in the paper of Narita et al. (2010a). Panel(a) is a slice cut from the PSD_B (ω_sc, k ) at k_x = 0.0043 rad km⁻¹ and k_z = 0.0087 rad km⁻¹. After the Doppler shift correction, the shape of the slice changes from a rectangle to a parallelogram, which is shown in panel (b). For a proper integration, we require a box-shaped PSD_B (ω_pl, k ), so we reserve the distribution in the red rectangle in panel (b) and append the gray patch from its mirror counterpart using Equation (8). Panel (c) shows the resultant slice with frequencies in the plasma frame. The 4D PSD_B (ω_pl, k ) is an ensemble of all the slices like this one.

Zoom In Zoom Out Reset image size