Abstract
The Large High Altitude Air Shower Observatory (LHAASO) detected 12 gamma-ray sources above 100 TeV, which are the possible origins of Galactic cosmic-rays. We summarize the neutrino measurements by IceCube and ANTARES in the vicinity of LHAASO sources to constrain the contribution of hadronic gamma-rays in these sources. We find that the current observations constrain hadronic gamma-rays to contribute no more than ∼60% of the gamma-rays from the Crab Nebula. Gamma-rays from two LHAASO sources, LHAASO J1825−1326 and LHAASO J1907+0626, are dominated by leptonic components up to ∼200 TeV, under the hypotheses in the analysis by IceCube. The uncertainties of the constraint on the hadronic gamma-ray emission are discussed. We also constrain the total 100 TeV gamma-ray emission from TeV pulsar wind nebulae by relying on the remarkable sensitivity of LHAASO at that energy.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Cosmic-rays extending to energies of several PeV are believed to originate from Galactic sources called PeVatrons. It is hard to localize PeVatrons with only cosmic-ray observations because charged cosmic-rays below several PeV are deflected frequently by the magnetic field while traveling in the Galaxy. Fortunately, PeV cosmic-rays produce high-energy (>100 TeV) gamma-rays and neutrinos in collisions with the baryon background through hadronuclear (pp) interactions or with the radiation background through photohadronic (pγ) interactions. Those gamma-rays and neutrinos are good tracers of PeVatrons, as both of them travel in a straight line after escaping from the sources.
Gamma-rays can be produced through the hadronic process (pp or pγ) and/or leptonic process (inverse Compton scattering). The production mechanisms of the observed gamma-rays are usually unclear. However, compared with TeV gamma-rays, the production of ≳100 TeV gamma-rays via inverse Compton scattering suffers from more stringent Klein–Nishina suppression. The sources with ∼100 TeV emission have more chances of being cosmic-ray PeVatrons (e.g., HESS Collaboration et al. 2016; Albert et al. 2020a; Tibet ASγ Collaboration et al. 2021).
The Large High Altitude Air Shower Observatory (LHAASO) is a hybrid extensive air shower array for cosmic-ray and gamma-ray studies. Relying on the unprecedented sensitivity to gamma-rays of around hundreds of TeV, the Kilometer Square Array (KM2A) of LHAASO detected 12 gamma-ray sources above 100 TeV (Cao et al. 2021). They also observed PeV gamma-rays from the direction of the Cygnus region and Crab Nebula (The LHAASO Collaboration et al. 2021). These LHAASO gamma-ray sources provide us with a group of target sources for finding cosmic-ray PeVatrons. We should look for neutrino signals from these sources to pin down the answer.
The IceCube neutrino observatory is a cubic-kilometer array in deep ice at the South Pole and is currently the most sensitive detector for neutrinos from TeV to PeV. IceCube has carried out some approaches to search for neutrino sources from known Galactic sources but only gives upper limits for the flux. First, in the Source List Search (SLS), they select some known astrophysical sources to be Neutrino Source Candidates (NSCs) and search for neutrino signals from them individually (e.g., Aartsen et al. 2019). The signals are not significant enough. Second, because stacking may help enhance the signal-to-noise ratio and discover weak signals, IceCube also tries to search for neutrinos over some catalogs of known sources, i.e., a Stacked Source Search (SSS; e.g., Aartsen et al. 2020a). Still, only upper limits have been given to the neutrino flux so far. However, as neutrinos are produced together with gamma-rays in hadronic interactions, one can derive the upper limits of the hadronic gamma-ray flux from that of the neutrino flux, and hence constrain the contribution of the hadronic process.
With the goal of identifying Galactic cosmic-ray Pevatrons from the LHAASO-detected 100 TeV sources, in this work we use the neutrino measurements of NSCs in the vicinity of LHAASO sources and constrain the hadronic contributions to gamma-ray emissions. In Section 2, we introduce the neutrino source searches used in this paper and the criteria for selecting the NSCs. In Section 3, we show the method to derive the upper limits on the hadronic gamma-ray flux. In Section 4, we compare the gamma-ray observations with the upper limits of the hadronic gamma-ray flux. In Section 5, we discuss previous works and evaluate the uncertainties in the analyses. We finally give conclusions in Section 6.
2. Source Selection
IceCube uses track-like neutrino events to measure the astrophysical neutrino flux from NSCs. The median location errors of these neutrinos range from 0 25 (above PeV) to 1° (sub-TeV; Aartsen et al. 2020a), while most LHAASO sources represent diffuse structures with angular extensions as large as 1° except for the Crab Nebula and LHAASO J2108+5157 (Cao et al. 2021). Astrophysical neutrinos from the directions of LHAASO sources probably have the same origins as those of gamma-rays.
25 (above PeV) to 1° (sub-TeV; Aartsen et al. 2020a), while most LHAASO sources represent diffuse structures with angular extensions as large as 1° except for the Crab Nebula and LHAASO J2108+5157 (Cao et al. 2021). Astrophysical neutrinos from the directions of LHAASO sources probably have the same origins as those of gamma-rays.
We select the NSCs within 1° from the measured center of a LHAASO source (see Table 1). The NSCs are taken from three SLSs: the 10 yr search (Aartsen et al. 2020a), the 8 yr search (Aartsen et al. 2019), and the combined search by ANTARES and IceCube (Albert et al. 2020b). The upper limits of the neutrino flux given by SLSs depend on the hypotheses on spectral shapes (usually assumed as a single power law) and the point-source hypothesis. We also choose the NSCs from two SSSs: the TeV Pulsar Wind Nebulae (PWNe) search (Aartsen et al. 2020b) and the Galactic catalog searches (Aartsen et al. 2017b) including five catalogs (one Milagro catalog, one HAWC catalog, and three supernova remnant (SNR) catalogs). The upper limits given by SSSs depend on not only the spectral shapes and assumed source extensions, but also the weighting factors of neutrino flux from individual sources in that specific catalog. The weighting factor is the fraction of neutrino flux from individual sources and depends on the weighting scheme used. The details on the weighting schemes are explained in Appendix A.
Table 1. Neutrino Source Candidates within 1° Away from the Measured Center of Each LHAASO Source
| LHAASO Source | Neutrino Source | Distance | Angular Distance | Extension |
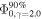
|
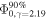
|
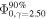
|
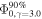
| Neutrino Source Search |
|---|---|---|---|---|---|---|---|---|---|
| Candidate | (kpc) | (deg) | (deg) | (10−17 TeV−1 cm−2 s−1) | |||||
| LHAASO J0534+2202 | Crab Nebula | 2.0 (a) | 0.08 | PS | 3.7 | ⋯ | ⋯ | 0.76 | 10 yr (d) |
| 0.08 | PS | 4.74 | ⋯ | ⋯ | ⋯ | 8 yr (e) | |||
| 0.08 | PS | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe (g) | |||
| 0.06 | PS | ⋯ | ⋯ | 117 | ⋯ | SNR with PWN (h) | |||
| LHAASO J1825−1326 | HESS J1826−130 | 4.0 (a) | 0.44 | PS | 13 | ⋯ | 25 | ⋯ | ANTARES & IceCube (f) |
| HESS J1825−137 | 3.9 (a) | 0.39 | 0.461 | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe | |
| 1HWC J1825−133 | 3.9 (a) | 0.21 | 0.5 | ⋯ | ⋯ | 0.948 | ⋯ | HAWC Hotspots (h) | |
| LHAASO J1839−0545 | HESS J1841−055 | ⋯ | 0.34 | PS | 4.8 | ⋯ | ⋯ | 3.28 | 10 yr |
| 1HWC J1838−060 | ⋯ | 0.43 | 0.5 | ⋯ | ⋯ | 0.948 | ⋯ | HAWC Hotspots | |
| LHAASO J1843−0338 | HESS J1843−033 | ⋯ | 0.35 | PS | 2.5 | ⋯ | ⋯ | 1.09 | 10 yr |
| 1HWC J1844−031c | ⋯ | 0.60 | 0.5 | ⋯ | ⋯ | 0.948 | ⋯ | HAWC Hotspots | |
| 1HWC J1842−046c | ⋯ | 0.98 | 0.5 | ⋯ | ⋯ | 0.948 | ⋯ | HAWC Hotspots | |
| LHAASO J1849−0003 | HESS J1849−000 | 7 (a) | 0.09 | PS | 2.2 | ⋯ | ⋯ | 1.01 | 10 yr |
| IGR J18490−0000 | 7 (a) | 0.11 | 0.09 | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe | |
| LHAASO J1908+0621 | MGRO J1908+06 | ⋯ | 0.21 | PS | 5.7 | ⋯ | ⋯ | 2.11 | 10 yr |
| 0.10 | PS | 7.62 | ⋯ | ⋯ | ⋯ | 8 yr | |||
| 0.49 | 1.3 | ⋯ | ⋯ | 3.98 | ⋯ | Milagro Six (h) | |||
| 1HWC J1907+062c | ⋯ | 0.29 | 0.5 | ⋯ | ⋯ | 0.948 | ⋯ | HAWC Hotspots | |
| LHAASO J2018+3651 | MGRO J2019+37 | ⋯ | 0.09 | PS | 4.0 | ⋯ | ⋯ | 0.69 | 10 yr |
| 0.38 | PS | 4.54 | ⋯ | ⋯ | ⋯ | 8 yr | |||
| 0.08 | 0.75 | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe | |||
| 0.16 | 0.64 | ⋯ | ⋯ | 3.98 | ⋯ | Milagro Six | |||
| LHAASO J2032+4102 | 2HWC J2031+415 | 1.8 (a) | 0.47 | PS | 9.2 | ⋯ | ⋯ | 1.42 | 10 yr |
| Cyg OB2 | 1.5 (b) | 0.18 | PS | 7.64 | ⋯ | ⋯ | ⋯ | 8 yr | |
| Cyg X-3 | 7.4 (c) | 0.10 | PS | 8.20 | ⋯ | ⋯ | ⋯ | 8 yr | |
| MGRO J2031+41 | ⋯ | 0.39 | 1.5 | ⋯ | ⋯ | 3.98 | ⋯ | Milagro Six | |
| TeV J2032+4130 | 1.8 (a) | 0.46 | 0.158 | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe | |
| LHAASO J2226+6057 | Boomerang | 0.8 (a) | 0.30 | 0.22 | 10.7 | 11.8 | 10.7 | ⋯ | TeV PWNe |
Note. Column 3 shows the distances between the candidates and Earth, which are derived from (a) TeVCat (http://tevcat2.uchicago.edu); (b) Mel'Nik & Dambis (2009); (c) McCollough et al. (2016). Column 4 shows the angular distances between the candidates and LHAASO sources. Column 5 shows the extensions of neutrino source candidates considered in the neutrino source searches. Columns 6–9 show the 90% C.L. upper limits of neutrino flux parameterized as  . The coordinates, extensions, and neutrino flux of neutrino source candidates are derived from SLSs: (d) the 10 yr point-source search (Aartsen et al. 2020a), (e) the 8 yr point-source search (Aartsen et al. 2019), (f) the ANTARES and IceCube combined search (Albert et al. 2020b) and SSSs: (g) the TeV PWNe search (Aartsen et al. 2020b), (h) the Galactic catalog searches (Aartsen et al. 2017b). The upper limits for E−3 spectrum in the 10 yr search are taken from Figure 3 of Aartsen et al. (2020a). The data point of the specific source in Figure 3 can be identified with the source decl. and local pretrial p-value in Table 3 of Aartsen et al. (2020a). The lower p-value indicates the higher upper limit for the sources with similar decl. angles. As for TeV PWNe search, only the upper limits for the inverse age-weighting scheme are displayed.
. The coordinates, extensions, and neutrino flux of neutrino source candidates are derived from SLSs: (d) the 10 yr point-source search (Aartsen et al. 2020a), (e) the 8 yr point-source search (Aartsen et al. 2019), (f) the ANTARES and IceCube combined search (Albert et al. 2020b) and SSSs: (g) the TeV PWNe search (Aartsen et al. 2020b), (h) the Galactic catalog searches (Aartsen et al. 2017b). The upper limits for E−3 spectrum in the 10 yr search are taken from Figure 3 of Aartsen et al. (2020a). The data point of the specific source in Figure 3 can be identified with the source decl. and local pretrial p-value in Table 3 of Aartsen et al. (2020a). The lower p-value indicates the higher upper limit for the sources with similar decl. angles. As for TeV PWNe search, only the upper limits for the inverse age-weighting scheme are displayed.
Download table as: ASCIITypeset image
Nine LHAASO sources have NSCs in the neighborhood. In order to compare the gamma-ray emission with neutrino emission in the range of TeV to PeV, we utilize previous TeV gamma-ray measurements of the certain NSCs to obtain the energy spectra at lower energies. The details about the TeV gamma-ray observations of the NSCs are described in Appendix B.
3. Method
In hadronuclear scenarios, the differential flux of gamma-rays and neutrinos ( ) are related as
) are related as
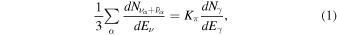
where α represents the neutrino flavor, Eγ
= 2Eν
, and Kπ
≃ 2 is the number ratio of charged to neutral pions. For a  spectrum, the upper limit on the hadronic gamma-ray flux at 100 TeV can be expressed as
spectrum, the upper limit on the hadronic gamma-ray flux at 100 TeV can be expressed as

where  is the 90% upper limit of neutrino flux.
is the 90% upper limit of neutrino flux.
Gamma-rays are partially absorbed during the propagation through the interstellar radiation field (ISRF) and cosmic microwave background (CMB) due to pair productions (γ γ → e+ e−). Such absorption is considered in the conversion of the neutrino upper limit into the gamma-ray upper limit, if the distance to the NSC is available. The ISRF energy density is taken from Popescu et al. (2017). Gamma-ray absorption around the source is not considered.
4. Results
The constraints on the hadronic gamma-ray emissions derived from SLSs are shown in Figure 1. If there is more than one NSCs associated with the LHAASO source, we only show the upper limit derived from the NSC closest to the center. The upper limit for the E−2 spectrum is generally consistent with or higher than the observed gamma-ray flux around 100 TeV in each panel. The upper limits for E−3 and E−2.5 are also generally consistent with the observed gamma-ray flux from 10 to 100 TeV but much higher at the energies below 10 TeV (see panels (b), (c), (d), (f), and (g)). We also show in the figure the energy range corresponding to where 90% of the signal neutrino events will be concentrated in. This energy range is determined by the assumed neutrino spectrum, as well as the effective area of the neutrino detector. The gamma-ray absorption due to ISRF and CMB is not significant around 100 TeV.
Figure 1. Comparison between the gamma-ray flux by LHAASO observations and the upper limits of the hadronic gamma-ray flux derived from SLSs. The gray lines present the 90% upper limits of the hadronic gamma-ray flux, where the dark parts mark the central 90% energy ranges according to neutrino observations. The solid, dotted–dashed, and dashed lines correspond to E−2.0, E−2.5, and E−3.0 neutrino spectra, respectively. The blue symbols are LHAASO observations (Cao et al. 2021; The LHAASO Collaboration et al. 2021). Other symbols and shaded areas are the gamma-ray measurements of (a) the Crab Nebula by Tibet ASγ (Amenomori et al. 2019), H.E.S.S. (Aharonian et al. 2006), and MAGIC (Albert et al. 2008); (b) HESS J1826−130 (H.E.S.S. Collaboration et al. 2020), HESS J1825−137 (H.E.S.S. Collaboration et al. 2019), eHWC J1825−134 (Abeysekara et al. 2020); (c) HESS J1841−055 (Aharonian et al. 2008); (d) HESS J1843−033 and HESS J1844−030 (H.E.S.S. Collaboration et al. 2018), and 2HWC J1844−032 (Abeysekara et al. 2017); (e) HESS J1849−000 (H.E.S.S. Collaboration et al. 2018); (f) HESS J1908+063 (Aharonian et al. 2009) and eHWC J1907+063 (Abeysekara et al. 2020); (g) VER J2019+368 (Abeysekara et al. 2018), and eHWC J2019+368 (Abeysekara et al. 2020); (h) Cyg X-3 (Sinitsyna & Sinitsyna 2020), TeV J2032+4130 (Aliu et al. 2014), MGRO J2031+41 (Abdo et al. 2007, 2009), and 2HWC J2031+415 (Abeysekara et al. 2017). The gamma-ray absorption due to ISRF and CMB is considered if the distance is available.
Download figure:
Standard image High-resolution imageThe constraints on the hadronic gamma-ray emissions derived from SSSs are shown in Figure 2. The hadronic gamma-ray flux from individual sources in the catalog should be lower than the upper limit derived from stacking the neutrino flux. The upper limit given by the HAWC catalog sets strong constraints on LHAASO J1825−1326 (panel (b)) and LHAASO J1908+0621 (panel (f)) above 100 TeV. The leptonic component is even dominant around 200 TeV. For the TeV PWNe, only the upper limits for inverse age weighting are shown because they are lower than those for the other weighting schemes and give stronger constraints on the hadronic gamma-rays (Aartsen et al. 2020b). The constraints above are reliable when the hypotheses in SSSs are consistent with the real case. In the HAWC catalog search, the sources are assumed to be 0 5 extended, and the neutrino flux following an E−2.5 spectrum is assumed to be proportional to the gamma-ray flux at the pivot energy for each source. The assumption on the neutrino flux ratio brings a large uncertainty to the upper limit estimate (see Section 5.2).
5 extended, and the neutrino flux following an E−2.5 spectrum is assumed to be proportional to the gamma-ray flux at the pivot energy for each source. The assumption on the neutrino flux ratio brings a large uncertainty to the upper limit estimate (see Section 5.2).
Figure 2. Comparison between the gamma-ray flux from the LHAASO observations and the upper limits of the hadronic gamma-ray flux derived from SSSs. Lines show the 90% upper limits of the hadronic gamma-ray flux, where the dark parts mark the central 90% energy ranges according to neutrino observations. The solid, dotted, dotted–dashed, and dashed lines correspond to E−2.0, E−2.19, E−2.5, and E−3.0 neutrino spectra, respectively. The colors of lines represent different source catalogs: black lines correspond to the TeV PWNe catalog (inverse age weighting), red lines to the catalog of SNRs with associated PWNe, green lines to the HAWC catalog, and purple lines to the Milagro catalog. The symbols in panel (i) are the gamma-ray flux from G106+2.7 observed by VERITAS (Acciari et al. 2009) and Tibet ASγ (Tibet ASγ Collaboration et al. 2021), MRGO C4 (Abdo et al. 2007, 2009), and LHAASO J2227+6057 (Cao et al. 2021). The symbols and shaded areas in other panels are the same as those in Figure 1.
Download figure:
Standard image High-resolution imageWe further estimate the cumulative gamma-ray flux from TeV PWNe with LHAASO observations and compare it to the upper limits given by the TeV PWNe search in the Figure 3. In the TeV PWNe search, Aartsen et al. (2020b) compared the differential upper limits for different weightings with the cumulative gamma-ray flux extrapolated from TeV observations to constrain the hadronic component from TeV to 100 TeV. Six of these PWNe are associated with LHAASO sources, while seven of them are not detected but in the sky declination band ( ) where data were taken by LHAASO-KM2A. With the observations at 100 TeV, we correct the extrapolated gamma-ray spectrum as the black solid line in Figure 3 (details in Appendix C). The cumulative gamma-ray flux at 100 TeV is 26% lower than the extrapolated value (gray dashed line) but still consistent within the uncertainty (gray shaded area).
) where data were taken by LHAASO-KM2A. With the observations at 100 TeV, we correct the extrapolated gamma-ray spectrum as the black solid line in Figure 3 (details in Appendix C). The cumulative gamma-ray flux at 100 TeV is 26% lower than the extrapolated value (gray dashed line) but still consistent within the uncertainty (gray shaded area).
Figure 3. The cumulative gamma-ray flux from TeV PWNe compared with the upper limits of hadronic gamma-ray flux. There are 35 PWNe in the catalog. The cumulative gamma-ray flux from all PWNe (black solid line) is 26% lower than the cumulative gamma-ray flux extrapolated from low energies before the LHAASO measurement (gray dashed line). The light-gray shaded area indicates the uncertainty of the extrapolated spectrum. Colored lines show the upper limits on the hadronic gamma-ray emission for four weighting schemes (Aartsen et al. 2020b).
Download figure:
Standard image High-resolution image5. Discussion
5.1. Comparison with Previous Works
We compare the neutrino spectrum model of the Crab Nebula in Kappes et al. (2007) with the neutrino observation results in the 10 yr search. First of all, the upper limit on neutrino flux (with a certain spectral shape)  is related to the upper limit on the signal event number n90 as
is related to the upper limit on the signal event number n90 as
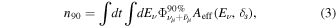
where Aeff is the effective area for neutrinos from the direction of the source (Eν is the neutrino energy and δs is the decl. of the source). The effective area is available in the IceCube muon-track data from 2008 to 2018 (IceCube Collaboration et al. 2021).
In the 7 yr search, one has n90 = 7.0 and 21.2 for the spectra of E−2 and E−3, respectively (Aartsen et al. 2017a). The two values both decrease in the 10 yr search (Aartsen et al. 2020a; n90 = 5.8 and 20.4, respectively). Note that the local pretrial p-value for the Crab Nebula is larger in the 10 yr search (from 0.34 in the 7 yr search to 0.49), indicating it is more background like. Therefore, we assume that n90 using the Kappes model decreases between the two searches. For the Kappes model, a value of n90 = 20.5 is derived from the 7 yr limit (Aartsen et al. 2017a) with Equation (3), which can be considered as the upper limit for 10 yr search, and hence results in a flux limit (red line in Figure 4) using Equations (3) and (1).
Figure 4. The best-fit gamma-ray spectrum Φγ
(black line) of the Crab Nebula and the upper limit of hadronic gamma-ray flux  (red line). The dark part of red line shows the central 90% energy range of signal events.
(red line). The dark part of red line shows the central 90% energy range of signal events.
Download figure:
Standard image High-resolution imageWe fit the gamma-ray observations with a log-parabola model  (black line in Figure 4). The number of hadronic gamma-rays in the central 90% energy range contributes
(black line in Figure 4). The number of hadronic gamma-rays in the central 90% energy range contributes  to the total gamma-rays at most, while the energy of hadronic gamma-rays contributes 62% ± 4% at most. Thus, the current observations suggest that the hadronic contribution cannot account for the bulk of the gamma-ray emission from the Crab Nebula.
to the total gamma-rays at most, while the energy of hadronic gamma-rays contributes 62% ± 4% at most. Thus, the current observations suggest that the hadronic contribution cannot account for the bulk of the gamma-ray emission from the Crab Nebula.
Furthermore, there have been many discussion in the literature on the hadronic gamma-ray and neutrino emission from potential Galactic PeVatrons and the Galactic plane, say, for PWNe (e.g., Amato et al. 2003), SNRs (e.g., Mandelartz & Becker Tjus 2015), young massive star clusters (YMCs; e.g., Anchordoqui et al. 2007), and diffuse Galactic gamma-ray and neutrino emission (Ahlers & Murase 2014; Neronov et al. 2014). Some TeV gamma-ray sources have been well studied to evaluate their probability of being PeVatrons, like the Cygnus Region (e.g., Anchordoqui et al. 2007), MGRO J2019+37 (e.g., Beacom & Kistler 2007), and MGRO J1908+06 (e.g., Halzen et al. 2017). However, the LHAASO-detected 100 TeV sources provide a group of sample sources for candidate PeVatrons. The high sensitivity of LHAASO at the 100 TeV range also helps to put stringent constraints on the PeVatron models. A wide range of parameter space in the Crab Nebula model by Amato et al. (2003) can be constrained by LHAASO observations at 100 TeV.
5.2. Uncertainties in the Analysis
The upper limit on the hadronic gamma-ray flux depends on the hypothesis of source extension. As the signals are not that significant over the background, the upper limit ratio for the extended-source (ES) hypothesis can be approximated as  , where
, where  is the upper limit for the point-source (PS) hypothesis, ΩES is the angular size of the extended source, and ΩPSF is the angular size of the point-spread function. The angular size is defined as
is the upper limit for the point-source (PS) hypothesis, ΩES is the angular size of the extended source, and ΩPSF is the angular size of the point-spread function. The angular size is defined as  and
and  , where σs
is the source extension and σIC = 0
, where σs
is the source extension and σIC = 0 64 is given by Halzen et al. (2017). Three LHAASO sources (LHAASO J1825−1326, LHAASO J1908+0621, and LHAASO J2226+6057) have extension measurements with a Gaussian template. They are 0
64 is given by Halzen et al. (2017). Three LHAASO sources (LHAASO J1825−1326, LHAASO J1908+0621, and LHAASO J2226+6057) have extension measurements with a Gaussian template. They are 0 30, 0
30, 0 58, and 0
58, and 0 36, respectively (Cao et al. 2021). If their neutrino counterparts have the same extensions, their upper limits will be 10%, 35%, and 15% higher in comparison with the PS hypothesis. The upper limits given by SLSs will be harder to constrain than the hadronic component for extended sources (panels (b)–(h) of Figure 1), while source extensions have been considered in SSSs (e.g., HAWC sources in the Galactic catalog searches are assumed to be 0
36, respectively (Cao et al. 2021). If their neutrino counterparts have the same extensions, their upper limits will be 10%, 35%, and 15% higher in comparison with the PS hypothesis. The upper limits given by SLSs will be harder to constrain than the hadronic component for extended sources (panels (b)–(h) of Figure 1), while source extensions have been considered in SSSs (e.g., HAWC sources in the Galactic catalog searches are assumed to be 0 5 extended).
5 extended).
The upper limit on the hadronic gamma-ray flux also relies on the hypothesis of the spectral shapes. A Bayesian analysis of the IceCube muon-track data from 2008 to 2018 is carried out to test the impact of spectral shapes on the upper limits (T. -Q. Huang & Z. Li 2021, in preparation). The hadronic component is assumed to follow the best-fit gamma-ray spectrum with a scaling factor. Five LHAASO sources are tested: LHAASO J0534+2202 (Crab Nebula), LHAASO J1825–1326, LHAASO J1908+0621, LHAASO J2018+3651, and LHAASO J2226+6057. Only the hadronic gamma-ray component of the Crab Nebula is well constrained to be no more than 70% of the total gamma-ray flux. As for the other sources, the upper limits on the hadronic gamma-ray flux are higher than the flux observed.
The weighting schemes used in the SSSs strongly influence the upper limit estimate. In the TeV PWNe search, the upper limit for the equal weighting is around 3 times that for the gamma-ray flux weighting (see the right panel of Figure 3). In the stacking search for neutrinos from active galactic nucleus and starburst galaxies, the upper limits for the equal weighting vary from 0.9 to 6.1 times the upper limits for the gamma-ray flux weighting when changing source samples. In the HAWC catalog search, the neutrino flux from each source is assumed to be proportional to the gamma-ray flux at the pivot energy. If the upper limits derived from the HAWC catalog search (green lines in Figure 2) increase by a factor of 6, we cannot simply use the upper limit on the stacking neutrino flux to constrain the hadronic gamma-ray flux from LHAASO J1908+0621 and LHAASO J1825−1326.
Kappes et al. (2007) approximate the neutrino and gamma-ray relation as Φν (E) = (0.694 − 0.16γ)Φγ (E), especially for the primary proton spectrum being E−γ (1.8 < γ < 3.0) with a high-energy exponential cutoff. If using this approximation, our upper limits on the hadronic gamma-ray flux will be increased by 34% (17%) for the E−2 (E−3) spectrum.
The radiation background around LHAASO sources also influences the constraints on the hadronic gamma-ray component. The gamma-ray sources associated with young massive stars may have a denser infrared background compared with the ISRF. The higher optical depths around 100 TeV induce the lower upper limits on the hadronic gamma-ray flux observed. In the photon-rich environment, pγ interactions should also be considered in addition to pp interactions.
6. Conclusions
We adopt the neutrino observation results in the directions within 1° from LHAASO sources and transform the neutrino upper limits into those of the hadronic gamma-ray flux. The upper limits derived from the SLSs are marginally consistent with the gamma-ray flux for most LHAASO sources and cannot constrain the hadronic contributions stringently. The upper limits derived from the SSSs set strong constraints on the hadronic components above 100 TeV. These constraints depend not only on the hypotheses of the spectral shapes and source extensions but also on the weighting schemes.
The main conclusions of this paper are summarized below:
(i) The hadronic gamma-ray component contributes no more than 62% for the Crab Nebula.
(ii) LHAASO J1825−1326 and LHAASO J1908+0621 are leptonic dominant up to 200 TeV, following the assumption that each source in the HAWC catalog has an intrinsic extension of ≲0 5 and follows an E−2.5 spectrum with the neutrino flux proportional to its gamma-ray flux at the pivot energy.
5 and follows an E−2.5 spectrum with the neutrino flux proportional to its gamma-ray flux at the pivot energy.
(iii) The cumulative gamma-ray flux from TeV PWNe is lower by 26% at 100 TeV than the extrapolation from low energies before the LHAASO measurement, leaving more room for hadronic-dominated emission.
The constraints on the hadronic gamma-ray flux will be stronger as the neutrino statistics increase in the following 10 yr. For IceCube, the time evolution of the 5σ discovery potential is close to 1/T (T is the observation time; Aartsen et al. 2017a). We take the discovery potential in the 10 yr point-source search as the baseline, corresponding to the data from 2008 to 2018. IceCube will be able to discover that the point-like neutrino source is two times fainter by 2028. If the intrinsic gamma-ray spectrum of LHAASO J1849−0003 follows E−2 up to PeV, neutrino observations with sensitivity two times better will offer more clues to determine the origins of these high-energy gamma-rays.
A stacking search for astrophysical neutrinos from the 12 LHAASO sources, which will increase the significance of signals and constrain the hadronic component more strictly, is required. As for the LHAASO sources in the southern sky (δ < −5°), the joint search of IceCube and ANTARES will improve the sensitivity by a factor of ∼2 compared to both individual analyses (Albert et al. 2020b). The instrumental volume of the high-energy neutrino detectors will be three times larger when KM3NeT/ARCA (two blocks; Adrián-Martínez et al. 2016) and Baikal-GVD (15 clusters; Safronov et al. 2021) fully operate in the next 5–10 yr.
We thank Qinrui Liu, Jon Dumm, and Ruo-Yu Liu for useful discussions. This work is supported by the Natural Science Foundation of China (Nos. 11773003, U1931201) and the China Manned Space Project (CMS-CSST-2021-B11).
Appendix A: Weighting Schemes
The TeV PWNe search gave the upper limits for the stacking neutrino flux from 35 identified TeV PWNe under four weighting schemes (Aartsen et al. 2020b). Neutrino flux from each source in the catalog is assumed to be the same in the equal weighting, proportional to the gamma-ray flux at 1 TeV in the gamma-ray flux weighting, proportional to the inverse age of the pulsar in the inverse age weighting, and proportional to the pulsar frequency in the frequency weighting.
The Galactic catalog searches gave the upper limit of the stacking neutrino flux over five Galactic catalogs (Aartsen et al.2017b). In the Milagro catalog, the neutrino flux from each source is assumed to follow the model of Kappes et al. (2009). In the HAWC catalog, the neutrino flux from each source is assumed to be proportional to the gamma-ray flux at the pivot energy. In the other three SNR catalogs, the neutrino flux from each source is assumed to be equal.
Appendix B: TeV Gamma-Ray Observations
LHAASO J1825−1326—We take the gamma-ray spectrum of eHWC J1825−134 instead of that of 1HWC J1825−133 because 1HWC J1825−133 is reported as 2HWC J1825−134 in the 2HWC catalog (Abeysekara et al. 2017), while 2HWC J1825−134 is only 0 07 from eHWC J1825−134 (>56 TeV) (Abeysekara et al. 2020). The flux data points of HESS J1826−130 are raised by a factor of 2.37 from the original values if we consider a 2D Gaussian intrinsic extension of 0
07 from eHWC J1825−134 (>56 TeV) (Abeysekara et al. 2020). The flux data points of HESS J1826−130 are raised by a factor of 2.37 from the original values if we consider a 2D Gaussian intrinsic extension of 0 21 with the integration region of 0
21 with the integration region of 0 22 (H.E.S.S. Collaboration et al. 2020).
22 (H.E.S.S. Collaboration et al. 2020).
LHAASO J1839−0545—We only take the spectrum of HESS J1841−055 because 1HWC J1838−060 overlaps with the extension of HESS J1841−055, and its differential flux normalization is compatible with the previous measurements of HESS J1841−055 (Abeysekara et al. 2016). The flux data points of HESS J1841−055 are raised by a factor of 1.14 based on its intrinsic extension of 0 41 (0
41 (0 25) along the major (minor) axis and the integration region of 0
25) along the major (minor) axis and the integration region of 0 7 (Aharonian et al. 2008).
7 (Aharonian et al. 2008).
LHAASO J1843−0338—We take the observation of 2HWC J1844−032 because 1HWC J1844−031c is reported as 2HWC J1844−032 in the 2HWC gamma-ray catalog (Abeysekara et al. 2017).
LHAASO J1849−0003—We only take the spectrum of HESS J1849−000 because HESS J1849−000 is in spatial coincidence with IGR J18490−0000 (Terrier et al. 2008).
LHAASO J1908+0621—We take the spectrum of eHWC J1907+063. 1HWC J1907+062c is reported as 2HWC J1908+063 (Abeysekara et al. 2017), while 2HWC J1908+063 is a point source only 0 17 from eHWC J1907+063 (>56 TeV) (Abeysekara et al. 2020). The flux data points of HESS J1908+063 are raised by a factor of 2.39 for its intrinsic extension of 0
17 from eHWC J1907+063 (>56 TeV) (Abeysekara et al. 2020). The flux data points of HESS J1908+063 are raised by a factor of 2.39 for its intrinsic extension of 0 34 and the integration region of 0.5° (Aharonian et al. 2009).
34 and the integration region of 0.5° (Aharonian et al. 2009).
LHAASO J2018+3651—We take the spectrum of VER J2019+368 because it constitutes the bulk of the emission of MGRO J2019+37 (Abeysekara et al. 2018). The flux data points of VER J2019+368 are raised by a factor of 2.53 based on its intrinsic extension of 0 34 (0
34 (0 14) along the major (minor) axis and the integration region of 0
14) along the major (minor) axis and the integration region of 0 23. We also use the observation of eHWC J2019+368 because its angular distance to LHAASO J2018+3651 is only 0
23. We also use the observation of eHWC J2019+368 because its angular distance to LHAASO J2018+3651 is only 0 17, and it also has 100 TeV measurements Abeysekara et al. (2020).
17, and it also has 100 TeV measurements Abeysekara et al. (2020).
LHAASO J2032+4102—The energy spectrum of TeV J2032+4130 is raised by a factor of 1.72 based on its intrinsic extensions of  along the major (minor) axis with an integration region of
along the major (minor) axis with an integration region of  (Aliu et al. 2014).
(Aliu et al. 2014).
LHAASO J2226+6057—The VERITAS flux data points of G106.3+2.7 are raised by a factor of 1.59 based on its intrinsic extension of 0 27 (0
27 (0 18) along the major (minor) axis with an integration region of 0
18) along the major (minor) axis with an integration region of 0 32 (Acciari et al. 2009).
32 (Acciari et al. 2009).
For the NSCs not mentioned above, we simply take their gamma-ray measurements without adjustments.
Appendix C: Gamma-Ray Flux from TeV PWNe
There are six PWNe associated with LHAASO sources. We fit the gamma-ray spectra of these sources from TeV to sub-PeV. The best spectral fits are selected among the single power-law (PL) model  , the exponential cutoff power-law (ECPL) model
, the exponential cutoff power-law (ECPL) model  , and the log-parabola (LOGP) model
, and the log-parabola (LOGP) model  based on the corrected Akaike Information Criterion (AICC
; Hurvich & Tsai 1991). Both the gamma-ray measurements of the identified PWNe and the associated LHAASO sources are used in the fitting except for HESS J1825–137. The observations by LHAASO are not considered for HESS J1825–137 because HESS J1825–137 is just one of three sources composing the gamma-ray hotspot, and the gamma-ray flux at 100 TeV is not dominated by this PWN (Albert et al. 2021). The best-fit parameters are shown in Table C1 (rows 1–6).
based on the corrected Akaike Information Criterion (AICC
; Hurvich & Tsai 1991). Both the gamma-ray measurements of the identified PWNe and the associated LHAASO sources are used in the fitting except for HESS J1825–137. The observations by LHAASO are not considered for HESS J1825–137 because HESS J1825–137 is just one of three sources composing the gamma-ray hotspot, and the gamma-ray flux at 100 TeV is not dominated by this PWN (Albert et al. 2021). The best-fit parameters are shown in Table C1 (rows 1–6).
Table C1. The Gamma-Ray Spectral Parameters of the TeV PWNe Constrained by LHAASO's Observation
| PWN | γ1 | γ2 | Ec | Model | Distance |
|---|---|---|---|---|---|
| (TeV) | (kpc) | ||||
| Crab Nebula | 2.86 | 0.20 | ⋯ | LOGP | 2.0 |
| HESS J1825−137 | 2.42 | ⋯ | 31 | ECPL | 3.9 |
| IGR J18490−0000 | 1.99 | ⋯ | ⋯ | PL | 7.0 |
| MGRO J2019+37 | 2.19 | 0.81 | ⋯ | LOGP | 24.8 a |
| TeV J2032+4130 | 2.07 | ⋯ | 78 | ECPL | 1.8 |
| Boomerang | 2.28 | 0.35 | ⋯ | LOGP | 0.8 |
| CTA1 | 2.2 | ⋯ | 214 | ECPL | 1.4 |
| Geminga | 2.23 | ⋯ | 74 | ECPL | 0.25 |
| 2HWC J0700+143 | 2.17 | ⋯ | 196 | ECPL | 17.2 a |
| HESS J1831−098 | 2.1 | ⋯ | 188 | ECPL | 30.9 a |
| HESS J1837−069 | 2.54 | ⋯ | 80 | ECPL | 6.6 |
| MAGIC J1857.2+0263 | 2.2 | ⋯ | 119 | ECPL | 29.7 a |
Notes. Rows 1–6: The best-fit spectral parameters for the PWNe associated with LHAASO sources. Rows 7–12: The upper limits of the cutoff energy Ec for the PWNe in the region where data were taken but not discovered by LHAASO-KM2A. These parameters are corrected for interstellar absorption.
a The distance to the source at the border of ISRF given by Popescu et al. (2017).Download table as: ASCIITypeset image
There are seven PWNe in the of region −15° < δ < 75° (δ is decl. angle) where data were taken but not discovered by the KM2A half-array. The upper limit on the gamma-ray flux is 1.1 × 10−13 TeV cm−2 s−1 between 100 and 178 TeV (Cao et al. 2021). We fit the upper limit of the energy flux at the 100–178 TeV bin with the ECPL model, following the spectral index used in the TeV PWNe search (Aartsen et al. 2020b). The best-fit cutoff energies are also the upper limits of the cutoff energies Ec . The best-fit Ec is negative for SNR G054.1+00.3, so we just follow its spectrum in the TeV PWNe search. The upper limits of Ec for the other six sources are shown in Table C1 (rows 7–13).
The correction for the interstellar absorption is necessary for the 12 PWNe in Table C1. The distances to eight PWNe are available from TeVCat. 3 As for the other four PWNe, we place them at the border of the ISRF model (a cylinder with radius 24 kpc and half-height 10 kpc) given by Popescu et al. (2017) to get the maximum absorption to gamma-rays around 100 TeV so that we can get a conservative upper limit on the gamma-ray flux from these PWNe before absorption. The formula to calculate the gamma-ray opacity follows the equations in Section 3 of Moskalenko et al. (2006). This upper limit also holds when the gamma-rays from LHAASO sources are not from the PWNe, but from the associated SNRs or YMCs (e.g., Aharonian et al. 2019; Ge et al. 2021).
As for the other 22 PWNe outside the region where data were taken, we simply use the same spectra in the TeV PWNe search (Aartsen et al. 2020b). The sum of gamma-ray spectra obtained above is shown as the black solid line in Figure 3.







