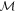Abstract
The observational value of the velocity dispersion, 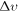 , is missing in the dark matter (DM) puzzle. Nonzero or nonthermal DM velocities can drastically influence large-scale structure and the 21 cm temperature at the epoch of the cosmic dawn, as well as the estimation of DM physical parameters, such as mass and interaction couplings. To study the phenomenology of
, is missing in the dark matter (DM) puzzle. Nonzero or nonthermal DM velocities can drastically influence large-scale structure and the 21 cm temperature at the epoch of the cosmic dawn, as well as the estimation of DM physical parameters, such as mass and interaction couplings. To study the phenomenology of 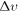 , we model the evolution of DM in terms of a simplistic and generic Boltzmann-like momentum distribution. Using cosmological data from the cosmic microwave background, baryonic acoustic oscillations, and red luminous galaxies, we constrain the DM velocity dispersion for a broad range of masses,
, we model the evolution of DM in terms of a simplistic and generic Boltzmann-like momentum distribution. Using cosmological data from the cosmic microwave background, baryonic acoustic oscillations, and red luminous galaxies, we constrain the DM velocity dispersion for a broad range of masses, 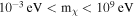 , finding
, finding 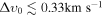 (99% CL). Including the Experiment to Detect the Global Epoch of Reionization Signature (EDGES) T21 measurements, we extend our study to constrain the baryon–DM interaction in the range of DM velocities allowed by our analysis. As a consequence, we present new bounds on two electromagnetic models of DM, namely minicharged particles (MCPs) and the electric dipole moment (EDM). For MCPs, the parameter region that is consistent with EDGES and independent bounds on cosmological and stellar physics is very small, pointing to the subelectronvolt mass regime of DM. A window in the MeV–GeV may still be compatible with these bounds for MCP models without a hidden photon. But the EDM parameter region consistent with EDGES is excluded by Big Bang nucleosynthesis and collider physics.
(99% CL). Including the Experiment to Detect the Global Epoch of Reionization Signature (EDGES) T21 measurements, we extend our study to constrain the baryon–DM interaction in the range of DM velocities allowed by our analysis. As a consequence, we present new bounds on two electromagnetic models of DM, namely minicharged particles (MCPs) and the electric dipole moment (EDM). For MCPs, the parameter region that is consistent with EDGES and independent bounds on cosmological and stellar physics is very small, pointing to the subelectronvolt mass regime of DM. A window in the MeV–GeV may still be compatible with these bounds for MCP models without a hidden photon. But the EDM parameter region consistent with EDGES is excluded by Big Bang nucleosynthesis and collider physics.
Export citation and abstract BibTeX RIS
1. Introduction
Within the current cosmological paradigm, where dark matter (DM) dominates the mass content of the universe, the nature of the DM particles plays a key role in shaping the linear matter power spectrum (MPS) and the angular power spectrum of the cosmic microwave background (CMB) anisotropies. Since the earliest works on the topic, the empirical evidence has favored collisionless DM particles, whose velocity dispersion in the early universe is so small that perturbations of galaxy size or larger are not damped by free streaming; i.e., the particles are cold (Peebles 1982; Blumenthal et al. 1984; Davis et al. 1985). The cold DM scenario is actually fully consistent with current CMB and large-scale structure (LSS) data (see, e.g., Ade et al. 2016a; Aghanim et al. 2018). However, at small scales, this scenario seems to face issues, especially related to the abundance and properties of dwarf galaxies (for a recent review, see Bullock & Boylan-Kolchin 2017). Early studies based on N-body cosmological simulations have shown that these potential issues are alleviated if the DM particles are warm (Colín et al. 2000; Avila-Reese et al. 2001; Bode et al. 2001). More recent works using semianalytical models and N-body + hydrodynamics cosmological simulations confirm that the warm DM scenario for particle masses within a given range, while keeping the success of the cold DM one at large scales, helps to solve their potential issues at small scales (e.g., Lovell et al. 2012, 2016; Colín et al. 2015; Bozek et al. 2016; González-Samaniego et al. 2016; Bose et al. 2017; for more references, see the review by Abazajian 2017).
Thus, one of the key pieces of the DM puzzle remains up in the air: whether it is entirely cold or mildly warm. Moreover, none of the popular cold DM candidates have been detected so far, either directly or indirectly. Consequently, the broad window of DM possibilities is still open for a rich variety of particles conceived in extended theories of the standard model (SM). Among the most relevant and general properties of the DM particles are their rest mass mχ and relic velocity dispersion  . In this sense, it would be very useful to constrain these properties in a generic way with the CMB and LSS data.
. In this sense, it would be very useful to constrain these properties in a generic way with the CMB and LSS data.
On the other hand, the radio signal recently detected by the Experiment to Detect the Global Epoch of Reionization Signature (EDGES; Bowman et al. 2018) not only represents the first evidence of the epochs of the cosmic dawn, but its anomalous absorption profile also suggests the first sign of DM nongravitational interactions with baryons. The observed absorption trough was found too deep compared to previous theoretical notions, albeit one explanation (among others discussed below) could be that baryons were cooled down through some interaction with DM (see, e.g., Dvorkin et al. 2014; Tashiro et al. 2014; Muñoz et al. 2015; Barkana 2018; Berlin et al. 2018; Safarzadeh et al. 2018). In this regard, noteworthy studies have included cosmological data such as the CMB and Lyα forest, providing valuable insights into the physics involving baryon–DM interactions, especially in the mass regime above MeV (Chen et al. 2002; Boddy & Gluscevic 2018; Boddy et al. 2018; Gluscevic & Boddy 2018; Kovetz et al. 2018; Slatyer & Wu 2018; Xu et al. 2018). An important ingredient of this scenario that has received little attention is the DM relic velocity dispersion mainly for particles lighter than a few MeV, even though its effects may play a major role.
In this paper, we explore the limits of DM velocity dispersion using LSS and CMB data. Because for supermassive particles, the velocity dispersion would be irrelevantly small, we choose to explore a broad range of masses, from 10−3 to 109 eV. Using these limits and the 21 cm cosmic dawn observations, we propagate the phenomenology to explore their collisional cross section with baryons, taking a velocity-dependent interaction of the form σ ∝ v−4 and v−2. Following these prescriptions, we pay particular attention to the constraints on the DM minicharge and the electric dipole moment (EDM).
For our exploration, we employ the simplest assumption for a generic DM momentum distribution: the Boltzmann or Gaussian function. This is not only simple but arguably the most physically motivated momentum distribution for DM. For example, thermal relics of weakly interacting massive particles (WIMPs) would obey classical Maxwell–Boltzmann statistics. On the other hand, if axions or other weakly interacting slim particles (WISPs) were produced through a nonthermal injection or a phase transition, they would be described by a narrow Gaussian momentum distribution.
Throughout this paper, we adopt the term velocity dispersion as the expectation value 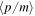 , weighted with a specific momentum distribution f(p). For thermal relics, this is known as the thermal velocity. Our focus is on the primordial velocity dispersion of DM particles through the study of cosmological data in the linear regime.5
, weighted with a specific momentum distribution f(p). For thermal relics, this is known as the thermal velocity. Our focus is on the primordial velocity dispersion of DM particles through the study of cosmological data in the linear regime.5
The rest of this paper is organized as follows. In Section 2 we briefly review the types of DM according to their mass and velocity dispersion. In Section 3 we constrain the DM velocity dispersion today, evolving a noninteracting fluid described by a Gaussian momentum distribution. Then, in Section 4 we connect our results with the mechanism of baryon–DM interactions proposed to cool down the baryonic gas. In Section 5, the constraints found on the mass, velocity, and scattering cross section are then translated to the DM minicharge and EDM. Our conclusions are summarized in Section 6.
2. Hot, Warm, and Cold DM
Before getting into the details of our analysis, it is worth briefly reviewing the general categories of DM. We do not intend to provide a comprehensive summary but simply to articulate the generic types of DM according to (not only their mass but) their velocity dispersion.
Cold DM is the most studied type of DM, for which the free-streaming scale is very small. Cold DM perturbations above this scale can be modeled as a perfect fluid with zero pressure or a collisionless fluid with zero velocity dispersion. Beyond the SM, theories like supersymmetry favor a large category of cold DM particle candidates called WIMPs, with masses 1 GeV ≲ mχ ≲ 3 TeV, which have been the target of most indirect and direct detection efforts (see, e.g., Gaskins 2016; Liu et al. 2017). If WIMPs were in thermal equilibrium in the early universe, they obeyed a Boltzmann momentum distribution 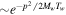 , whose associated thermal velocity is
, whose associated thermal velocity is 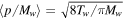 . This kind of heavy DM candidate should have decoupled very early in the radiation-dominated era from a cosmic plasma with a large number of relativistic degrees of freedom (dof)
. This kind of heavy DM candidate should have decoupled very early in the radiation-dominated era from a cosmic plasma with a large number of relativistic degrees of freedom (dof) 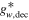 . From the conservation of the specific entropy, we know that the WIMPs' temperature is related to the radiation temperature as
. From the conservation of the specific entropy, we know that the WIMPs' temperature is related to the radiation temperature as 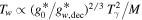 , where
, where 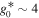 is the relativistic dof today. It is pretty clear that for extremely large masses, the WIMPs' temperature (and, consequently, their thermal velocity) would be extremely small as well.
is the relativistic dof today. It is pretty clear that for extremely large masses, the WIMPs' temperature (and, consequently, their thermal velocity) would be extremely small as well.
Axions are another noteworthy cold DM candidate. Originating from the Peccei–Quinn solution to the strong charge-parity problem (Peccei & Quinn 1977), the quantum chromodynamics (QCD) axion acquires a typical mass of 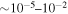 eV near the QCD phase transition (Marsh 2016). At this time, any interaction was already suppressed by the Peccei–Quinn scale; hence, axions would have been produced out of thermal equilibrium and are not subject to thermal velocities. A more general family of axion-like particles in a broad range of masses (10−24–103 eV) could also be produced nonthermally via the vacuum misalignment mechanism (Ringwald 2012). Furthermore, if by some mechanism, axions were brought into thermal equilibrium, they would undergo a Bose condensation (BEC; Sikivie & Yang 2009; Erken et al. 2012). In either case, axions shall be well described by a Boltzmann-like distribution,
eV near the QCD phase transition (Marsh 2016). At this time, any interaction was already suppressed by the Peccei–Quinn scale; hence, axions would have been produced out of thermal equilibrium and are not subject to thermal velocities. A more general family of axion-like particles in a broad range of masses (10−24–103 eV) could also be produced nonthermally via the vacuum misalignment mechanism (Ringwald 2012). Furthermore, if by some mechanism, axions were brought into thermal equilibrium, they would undergo a Bose condensation (BEC; Sikivie & Yang 2009; Erken et al. 2012). In either case, axions shall be well described by a Boltzmann-like distribution,  , where the momentum width Δp (extremely small for axion cold DM) encodes the physics of the process leading to the nonthermal state.6
, where the momentum width Δp (extremely small for axion cold DM) encodes the physics of the process leading to the nonthermal state.6
Though it is by far subdominant, hot DM is the best-known component of DM because it is mainly composed of active neutrinos (Abazajian & Kaplinghat 2016). Neutrinos were in thermal equilibrium in the early universe, obeying the Fermi momentum distribution in the relativistic limit 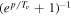 . Unlike for any other DM candidate, the decoupling temperature is fairly well known,
. Unlike for any other DM candidate, the decoupling temperature is fairly well known, 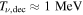 (Lesgourgues & Pastor 2006). At that time, only e± and γ contributed to the relativistic dof,
(Lesgourgues & Pastor 2006). At that time, only e± and γ contributed to the relativistic dof, 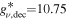 . After decoupling, their temperature is proportional to that of photons,
. After decoupling, their temperature is proportional to that of photons, 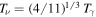 , and then simply gets redshifted. Neutrinos become nonrelativistic at late epochs composing a small fraction of matter today,
, and then simply gets redshifted. Neutrinos become nonrelativistic at late epochs composing a small fraction of matter today, 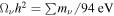 . The neutrino thermal velocity is completely parameterized in terms of mass,
. The neutrino thermal velocity is completely parameterized in terms of mass, 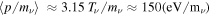 km s−1. The net effect of active neutrinos is to wash out the small-scale matter fluctuations above the free-streaming wavenumber
km s−1. The net effect of active neutrinos is to wash out the small-scale matter fluctuations above the free-streaming wavenumber 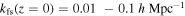 . For that reason, cosmological observations tightly constrain the sum of neutrino masses below the eV scale.
. For that reason, cosmological observations tightly constrain the sum of neutrino masses below the eV scale.
If a small fraction of axions somehow thermalized (see, e.g., Archidiacono et al. 2013), they would obey a Bose distribution 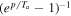 . Thermal axions (and any other subelectronvolt thermal species) are also hot DM candidates with a behavior close to that of active neutrinos.
. Thermal axions (and any other subelectronvolt thermal species) are also hot DM candidates with a behavior close to that of active neutrinos.
Warm DM is an interesting intermediate phase characterized by slow particles, albeit not zero pressure, and consequently has nonnegligible free-streaming scales. Sterile neutrinos are warm DM candidates well motivated from theory and invoked by some anomalies in short-baseline oscillation data (Lasserre 2014). They can mix with active neutrinos but do not carry weak interactions (Abbiendi et al. 2006). Inspired by the physics of active neutrinos, sterile neutrinos are often assumed to decouple thermally while being relativistic, obeying the Fermi distribution 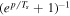 . In this case, the relic temperature is unknown, but it should be proportional to the photon temperature too,
. In this case, the relic temperature is unknown, but it should be proportional to the photon temperature too, 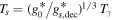 , where
, where 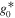 is the relativistic dof today.
is the relativistic dof today.
Studying sterile neutrino mass bounds is a twofold task: from LSS considerations and from indirect DM searches. Assuming a specific value for 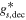 (for example, 106.75 in the SM and twice as much in supersymmetry), the thermal velocity and free-streaming scale become completely specified by the mass ms, and its effects can be constrained with measurements of the MPS data (especially through the Lyα forest for the scales of interest), leading this to a lower limit on ms (Abazajian 2017). On the other hand, a fraction of sterile neutrinos is expected to decay rapidly, leading to a source of monoenergetic photons with energy close to half of its mass. A hint of such a decay has been prompted by the discovery of an unidentified emission line at 3.5 keV in the stacked X-ray spectrum of galaxy clusters and galaxies (see Abazajian 2017, and references therein).
(for example, 106.75 in the SM and twice as much in supersymmetry), the thermal velocity and free-streaming scale become completely specified by the mass ms, and its effects can be constrained with measurements of the MPS data (especially through the Lyα forest for the scales of interest), leading this to a lower limit on ms (Abazajian 2017). On the other hand, a fraction of sterile neutrinos is expected to decay rapidly, leading to a source of monoenergetic photons with energy close to half of its mass. A hint of such a decay has been prompted by the discovery of an unidentified emission line at 3.5 keV in the stacked X-ray spectrum of galaxy clusters and galaxies (see Abazajian 2017, and references therein).
The majoron (a scalar boson proposed to explain the seesaw mechanism; Chikashige et al. 1981) is also a good warm DM candidate. With properties and effects similar to sterile neutrinos, they can be modeled with a thermal Bose momentum distribution  and a temperature
and a temperature 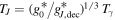 .
.
In general, thermal relics are defined by the relativistic dof at the moment of their decoupling 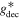 . Correspondingly, the thermal velocity is
. Correspondingly, the thermal velocity is 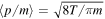 in the case of Boltzmann relics, 3.15T/m in the case of fermions, and 2.7T/m in the case of bosons. Evaluated today, the thermal velocity can be expressed as approximately equal for fermions and bosons,
in the case of Boltzmann relics, 3.15T/m in the case of fermions, and 2.7T/m in the case of bosons. Evaluated today, the thermal velocity can be expressed as approximately equal for fermions and bosons,
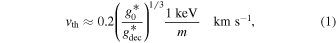
where Tcmb = 2.72 K is implicit. An equivalent parameterization, often used for warm DM, can be written explicitly indicating the DM abundance (Hogan & Dalcanton 2000; Bode et al. 2001),
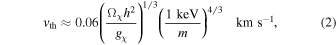
where gχ is the DM particle dof. These two expressions are equivalent and hold for relativistic Fermi and Bose thermal species. Similar expressions can be obtained for Boltzmann relics just by multiplying Equation (1) by 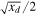 and Equation (2) by
and Equation (2) by 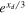 , where
, where 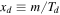 accounts for the precise time of DM kinetic decoupling.7
accounts for the precise time of DM kinetic decoupling.7
Nonthermal processes, however, are possible and play a crucial role in warm DM models. For example, an important fraction of sterile neutrinos could be resonantly produced (RP; Abazajian 2017). The RP sterile neutrinos are generated with small velocities characterized by a sharp distribution peaked at small momenta. The average momentum reduction is not unique and depends on the specific mechanism under consideration. For instance, the Shi–Fuller mechanism (Shi & Fuller 1999) predicts an average reduction of  (Laine & Shaposhnikov 2008; Boyarsky et al. 2009a). But Bezrukov et al. (2019) proposed a model implying even smaller values. In any case, the bounds on the sterile neutrino mass (or, equivalently, their velocity dispersion) become weaker in the case of resonant production compared to their thermal counterparts. Another possible source of nonthermal production is a late decay of heavy particles, inducing distortions to an otherwise thermal distribution (Cuoco et al. 2005). Lastly, a partial or full condensation of DM particles (Rodríguez-Montoya et al. 2013) is another example of nonthermal processes, which would relax the current constraints on the DM mass and velocities.
(Laine & Shaposhnikov 2008; Boyarsky et al. 2009a). But Bezrukov et al. (2019) proposed a model implying even smaller values. In any case, the bounds on the sterile neutrino mass (or, equivalently, their velocity dispersion) become weaker in the case of resonant production compared to their thermal counterparts. Another possible source of nonthermal production is a late decay of heavy particles, inducing distortions to an otherwise thermal distribution (Cuoco et al. 2005). Lastly, a partial or full condensation of DM particles (Rodríguez-Montoya et al. 2013) is another example of nonthermal processes, which would relax the current constraints on the DM mass and velocities.
Actually, it is not the DM mass but, more precisely, its velocity dispersion that defines the free-streaming length,
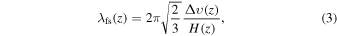
which determines the scale below which DM cannot remain gravitationally confined, or, equivalently, in Fourier space, the wavenumbers above which matter structures are washed out from the MPS. The comoving free-streaming wavenumber 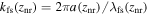 provides a rough approximation to know the k below which the free-streaming effects are negligible, where znr denotes the time of nonrelativistic transition. For thermal candidates, the free-streaming scale depends on the mass and
provides a rough approximation to know the k below which the free-streaming effects are negligible, where znr denotes the time of nonrelativistic transition. For thermal candidates, the free-streaming scale depends on the mass and  as they are given in Equation (1). In the case of nonthermal candidates, their velocity dispersion (and, consequently, their free-streaming scale) depends on the specific model of DM production.
as they are given in Equation (1). In the case of nonthermal candidates, their velocity dispersion (and, consequently, their free-streaming scale) depends on the specific model of DM production.
Now, irrespective of the precise nature of DM, their particles will be described by a momentum distribution denoted by f(p). Whenever DM interactions are negligible, f(p) evolves according to the Vlasov equation df/dt = 0, whose perturbations in Fourier space read (Ma & Bertschinger 1995)

where q = ap is the comoving momentum magnitude, 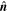 is the momentum unit vector,
is the momentum unit vector, 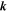 is the Fourier wavevector, and a is the scale factor. The dynamic variables are the scalar perturbations ψ, ϕ to the homogeneous Lemaître–Friedman metric, a linear statistical perturbation Ψ to f(p), and the comoving proper energy
is the Fourier wavevector, and a is the scale factor. The dynamic variables are the scalar perturbations ψ, ϕ to the homogeneous Lemaître–Friedman metric, a linear statistical perturbation Ψ to f(p), and the comoving proper energy 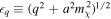 . In general, Equation (4) has to be solved as a Boltzmann hierarchy of differential equations. This is the case for hot and warm DM but not for cold DM. In the limit
. In general, Equation (4) has to be solved as a Boltzmann hierarchy of differential equations. This is the case for hot and warm DM but not for cold DM. In the limit  or
or  , one can cut the Boltzmann hierarchy (see, e.g., Dodelson 2003; Mo et al. 2010), and Equation (4) reduces to
, one can cut the Boltzmann hierarchy (see, e.g., Dodelson 2003; Mo et al. 2010), and Equation (4) reduces to
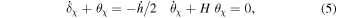
where 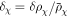 is the DM fluctuating overdensity, and θχ is the peculiar velocity. In synchronous gauge, θχ is zero, and cold DM is evolved only through δχ. The results obtained from this approach are valid strictly within the linear regime; as such, Δυ is scale-invariant and interpreted as the primordial DM velocity dispersion.
is the DM fluctuating overdensity, and θχ is the peculiar velocity. In synchronous gauge, θχ is zero, and cold DM is evolved only through δχ. The results obtained from this approach are valid strictly within the linear regime; as such, Δυ is scale-invariant and interpreted as the primordial DM velocity dispersion.
Well inside the nonlinear regime, DM particles are subject to violent processes depending on the scale and local environments (e.g., gravitational infall, astrophysical feedback effects, etc.) so that their phase density can be considerably modified. Although the latter is not our case of study, we mention that some interesting inferences have been attempted by comparing the primordial and coarse-grained DM phase densities (Tremaine & Gunn 1979; Madsen 1991; Hogan & Dalcanton 2000; Boyarsky et al. 2009b).
3. Generic Constraints on the DM Velocity Dispersion
The only knowledge about the DM momentum distribution fχ(p) is that it must be peaked at low momenta in order to describe nonrelativistic, (almost) pressureless matter. We argue that a Gaussian distribution is a good generic description because it represents a variety of DM scenarios, from heavy thermal relics to nonthermal distortions and even phase transitions. We implement the Gaussian momentum distribution

in class (Blas et al. 2011; Lesgourgues & Tram 2011), replacing the default cold DM with this non–cold DM module described by fχ(p). Here Δp is the momentum width and 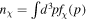 is the number density. Without regard to the (thermal or not) origin of DM, we can define a fiducial "temperature"
is the number density. Without regard to the (thermal or not) origin of DM, we can define a fiducial "temperature" 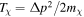 , in terms of which we can write the velocity dispersion
, in terms of which we can write the velocity dispersion 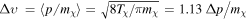 . Notice that the velocity dispersion gets linearly redshifted,
. Notice that the velocity dispersion gets linearly redshifted, 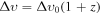 ,
, 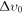 being the value measured today.
being the value measured today.
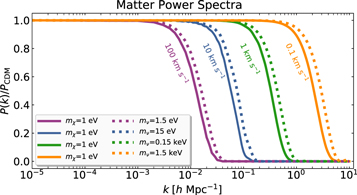
As mentioned in Section 2, the DM description with Equation (6) reduces to standard cold DM in the limit 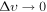 . This is reproduced in Figure 1, where we plot the MPS ratio (over cold DM) for fixed mχ = 1 eV but different values of
. This is reproduced in Figure 1, where we plot the MPS ratio (over cold DM) for fixed mχ = 1 eV but different values of 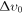 . These ratios progressively approach 1 for smaller values of
. These ratios progressively approach 1 for smaller values of 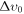 . An analogous effect is produced by a Fermi distribution that progressively approaches cold DM for masses in the keV range. But we recall that the velocity dispersion (not the mass) regulates the free-streaming scale for a given DM model. In Figure 1, we show both Gaussian and Fermi cases for equivalent velocity dispersions, from which we notice that the Gaussian distribution causes slightly more suppression on the MPS than Fermi. Thus, we are showing that the Gaussian distribution fχ(p) is a convenient description for DM because, through its parameters, it can cover hot, warm, and cold possible states of DM.
. An analogous effect is produced by a Fermi distribution that progressively approaches cold DM for masses in the keV range. But we recall that the velocity dispersion (not the mass) regulates the free-streaming scale for a given DM model. In Figure 1, we show both Gaussian and Fermi cases for equivalent velocity dispersions, from which we notice that the Gaussian distribution causes slightly more suppression on the MPS than Fermi. Thus, we are showing that the Gaussian distribution fχ(p) is a convenient description for DM because, through its parameters, it can cover hot, warm, and cold possible states of DM.
Figure 1. Distinct ratios of the MPS with respect to cold DM. The same color indicates the same velocity dispersion. Solid lines correspond to 1 eV mass DM particles described by the Gaussian distribution fχ, while dotted lines are thermal neutrinos described by the Fermi distribution. The neutrino thermal velocity is uniquely specified by its mass. In contrast, DM particles described with fχ approach cold DM as 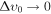 , irrespective of their mass.
, irrespective of their mass.
Download figure:
Standard image High-resolution imageOur primary goal is to obtain observational constraints for Δυ0 using public data surveys such as Planck (Ade et al. 2016b; Aghanim et al. 2016), baryonic acoustic oscillations (BAOs; Alam et al. 2017; Buen-Abad et al. 2018), and red luminous galaxies from the Sloan Digital Sky Survey (SDSS; Tegmark et al. 2006). We employ montepython (Audren et al. 2013; Brinckmann & Lesgourgues 2018) to perform Bayesian estimations using 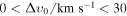 as a prior. Although we have seen that the CMB and MPS are insensitive to the DM mass (when
as a prior. Although we have seen that the CMB and MPS are insensitive to the DM mass (when 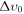 is varied independently), we choose to check for any marginal effect by splitting the analysis into six stages from subelectronvolt to GeV, as indicated in Table 1. For the rest of the cosmological parameters, we use customary flat priors. Additionally, for any pair values of Ωχ h2 and mχ, nχ gets internally rewritten by CLASS in order to satisfy the equation
is varied independently), we choose to check for any marginal effect by splitting the analysis into six stages from subelectronvolt to GeV, as indicated in Table 1. For the rest of the cosmological parameters, we use customary flat priors. Additionally, for any pair values of Ωχ h2 and mχ, nχ gets internally rewritten by CLASS in order to satisfy the equation 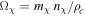 (where ρc is the critical density).
(where ρc is the critical density).
Table 1. Bounds on the DM Velocity Dispersion from the Six Mass-sampling Stages of the Analysis
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | Stage 6 | ||
|---|---|---|---|---|---|---|---|
| (10−3–10−1 eV) | (10−1–101 eV) | (101–103 eV) | (103–105 eV) | (105–107 eV) | (107–109 eV) | ||
| P | 1.32 | 1.31 | 1.33 | 1.34 | 1.31 | 1.33 | |
| PB |
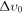 (km s−1) ≲ (km s−1) ≲ |
1.28 | 1.27 | 1.26 | 1.25 | 1.26 | 1.25 |
| PBS | 0.32 | 0.32 | 0.32 | 0.33 | 0.32 | 0.33 |
Note. Upper limits at 99% CL. The prior on the velocity dispersion is 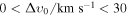 for every stage of the analysis. The data sets are denoted with P: Planck; PB: Planck + BAO BOSS; PBS: Planck + BAO BOSS + SDSS DR4 LRG.
for every stage of the analysis. The data sets are denoted with P: Planck; PB: Planck + BAO BOSS; PBS: Planck + BAO BOSS + SDSS DR4 LRG.
Download table as: ASCIITypeset image
After a deep exploration, the standard cosmological parameters are constrained in concordance with standard reports (Ade et al. 2016a). We find no significant degeneracies between Δυ0 and the standard cosmological parameters, suggesting an independent effect from our parameterization. As expected, the mass parameter mχ is unconstrained when the velocity dispersion is varied independently. As can be read from Table 1 and Figure 2, the constraints on  are not significantly different by comparing the six stages of mass sampling. The Planck and BAO BOSS data constrain the free-streaming effects that would be caused by a large DM velocity dispersion (similar to an increase on the effective number of relativistic species). But the most restrictive constraints on
are not significantly different by comparing the six stages of mass sampling. The Planck and BAO BOSS data constrain the free-streaming effects that would be caused by a large DM velocity dispersion (similar to an increase on the effective number of relativistic species). But the most restrictive constraints on 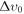 are obtained when the LSS data are included, because the free streaming suppresses the MPS on small scales. Summarizing the results, our analysis shows that cosmological data constrain the DM velocity dispersion to
are obtained when the LSS data are included, because the free streaming suppresses the MPS on small scales. Summarizing the results, our analysis shows that cosmological data constrain the DM velocity dispersion to
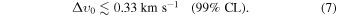
This translates to a lower bound on the epoch of DM nonrelativistic transition, 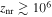 . But because
. But because 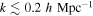 wavenumbers correspond to modes that entered the horizon at redshifts z ≲ 105, the free-streaming effects of a DM species with
wavenumbers correspond to modes that entered the horizon at redshifts z ≲ 105, the free-streaming effects of a DM species with 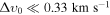 would not be noticeable at the scales of the LSS data used in our analysis.
would not be noticeable at the scales of the LSS data used in our analysis.
Figure 2. Constraints on the DM velocity dispersion after our analysis of the CMB and LSS data. The dark red line shows thermal velocities for warm DM using Equation (2), while the light red band is a 0.25 nonthermal correction (due to resonant production in the case of sterile neutrinos). Previous reports on sterile neutrino and thermal majorons are shown as candidates of warm DM. Reports on hot DM candidates, such as active neutrinos and thermal axions, are shown using Equation (1).
Download figure:
Standard image High-resolution imageIn Figure 2, we also mark the thermal velocity, using Equation (1), due to active neutrinos and thermal axions according to previous reports on their masses,  (Ade et al. 2016a) and
(Ade et al. 2016a) and  (Archidiacono et al. 2013). We also plot the thermal velocity given in Equation (2) with
(Archidiacono et al. 2013). We also plot the thermal velocity given in Equation (2) with 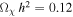 and gχ = 2 (dark red line). We should correct vth in two ways. First, we have to take into account the uncertainty on the mass, which is the most unknown parameter, leading us to the error propagation
and gχ = 2 (dark red line). We should correct vth in two ways. First, we have to take into account the uncertainty on the mass, which is the most unknown parameter, leading us to the error propagation 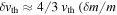 ). Unfortunately, we do not count on any measurement of the DM mass; thus, we adopt a conservative choice for the mass error δm = 0.3 m (roughly what might be expected after preliminary and speculative evidence of this parameter) that may help us for illustrative purposes. Second, we include a Shi–Fuller correction to relax the bounds in the case of resonant production of sterile neutrinos (light red band). Additionally, we ought to account for the uncertainty on the details of kinetic decoupling (e.g., the value of
). Unfortunately, we do not count on any measurement of the DM mass; thus, we adopt a conservative choice for the mass error δm = 0.3 m (roughly what might be expected after preliminary and speculative evidence of this parameter) that may help us for illustrative purposes. Second, we include a Shi–Fuller correction to relax the bounds in the case of resonant production of sterile neutrinos (light red band). Additionally, we ought to account for the uncertainty on the details of kinetic decoupling (e.g., the value of  or xd; see text below Equation (1)), but for illustrative purposes, we just depict the thermal velocity as it is shown in Equation (2). We also spot the mass constraint mJ = 0.158 ± 0.007 keV reported for thermal majorons as a warm DM candidate (Lattanzi et al. 2013). Thermally produced sterile neutrino bounds are still in debate; there is a controversy between lower bounds from cosmological data and upper bounds from diffuse X-ray emission (see the comprehensive reviews from Adhikari et al. 2017; Boyarsky et al. 2018). In contrast to thermal relics, RP sterile neutrinos do not need large mixing angles with active neutrinos to match the required DM abundance. As a consequence, RP sterile neutrino decay into X-rays may be suppressed, thereby loosening the mass upper bound. Recent analyses of Lyα forest data set a lower limit of ms ≳ 5.3 keV on thermally produced sterile neutrinos (Iršič et al. 2017, which is larger than previous determinations).8
Meanwhile, combined analyses of SDSS/BOSS and Lyα forest data set a lower limit of ms ≳ 3.5 keV on RP sterile neutrinos (Baur et al. 2017). A noteworthy recent report based solely on the EDGES signal measured timing sets a lower limit of ms ≳ 2 keV (Safarzadeh et al. 2018). On the other hand, the nonobservation of X-ray photons induced by the decay of sterile neutrinos sets an upper bound of ms ≲ 20 keV (Adhikari et al. 2017). All in all, we include in Figure 2 (black dashed lines) the mass constraints on both thermal and RP sterile neutrinos within 2 keV < ms < 20 keV, corresponding to a velocity dispersion within 5 × 10−5 km
or xd; see text below Equation (1)), but for illustrative purposes, we just depict the thermal velocity as it is shown in Equation (2). We also spot the mass constraint mJ = 0.158 ± 0.007 keV reported for thermal majorons as a warm DM candidate (Lattanzi et al. 2013). Thermally produced sterile neutrino bounds are still in debate; there is a controversy between lower bounds from cosmological data and upper bounds from diffuse X-ray emission (see the comprehensive reviews from Adhikari et al. 2017; Boyarsky et al. 2018). In contrast to thermal relics, RP sterile neutrinos do not need large mixing angles with active neutrinos to match the required DM abundance. As a consequence, RP sterile neutrino decay into X-rays may be suppressed, thereby loosening the mass upper bound. Recent analyses of Lyα forest data set a lower limit of ms ≳ 5.3 keV on thermally produced sterile neutrinos (Iršič et al. 2017, which is larger than previous determinations).8
Meanwhile, combined analyses of SDSS/BOSS and Lyα forest data set a lower limit of ms ≳ 3.5 keV on RP sterile neutrinos (Baur et al. 2017). A noteworthy recent report based solely on the EDGES signal measured timing sets a lower limit of ms ≳ 2 keV (Safarzadeh et al. 2018). On the other hand, the nonobservation of X-ray photons induced by the decay of sterile neutrinos sets an upper bound of ms ≲ 20 keV (Adhikari et al. 2017). All in all, we include in Figure 2 (black dashed lines) the mass constraints on both thermal and RP sterile neutrinos within 2 keV < ms < 20 keV, corresponding to a velocity dispersion within 5 × 10−5 km 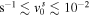 km s−1.
km s−1.
Figure 2 displays a wide region of allowed mχ and Δυ0 parameters; let us now place our bounds in context. We begin to recall that active neutrinos and thermal axions—as well as any other hot DM species—are clearly discarded as the main source of DM. In the case of thermal DM (or nonthermal DM with a correction of 0.25), keep in mind that the respective dark and light red bands bear large uncertainties in the mass and kinetic decoupling parameters, so we use them only for illustrative purposes. With that in mind, we might read that our bounds seem to disfavor thermal candidates (including nonthermal corrections) with masses below ≲40 eV. A previous report on thermal majorons (Lattanzi et al. 2013) is at the edge of but within our 99% CL bounds. Previous reports on thermal (Iršič et al. 2017) and resonant (Baur et al. 2017) sterile neutrinos are well below our 99% CL boundary. Notice again that our bounds do not exclude any DM mass from 10−3 to 109 eV. Indeed, warm (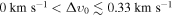 ) and cold (
) and cold (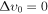 ) DM candidates are well allowed by our constraints, irrespective of their mass.
) DM candidates are well allowed by our constraints, irrespective of their mass.
4. Role of DM Velocity Dispersion on the 21 cm Signal
In many studies of 21 cm cosmology, it is customary to fix the DM mass to the WIMP scale, whose corresponding thermal velocity is nearly zero. But from the previous section, we see that a vast variety of DM candidates could involve a significant velocity dispersion while still reproducing the observed LSS and CMB spectra. Now we are going to use the constraints of Figure 2 in order to explore the 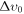 effects on the interpretation of the EDGES measurements.
effects on the interpretation of the EDGES measurements.
EDGES probes the epochs after primordial recombination and before the formation of the first luminous sources. During these epochs, the baryonic gas is mainly composed of neutral hydrogen with a total spin S = 0 (proton/electron antiparallel spins). When an atom in the parallel state (S = 1) realigns its spins, a photon is emitted with energy E21 = 5.87 μeV, equivalent to a wavelength of 21 cm. The 21 cm signal is the observed brightness temperature with respect to the photon background (for a comprehensive review, see Furlanetto et al. 2006; Morales & Wyithe 2010; Pritchard & Loeb 2012),
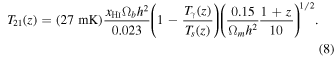
Here xHi (≈1 during the epoch of cosmic dawn) is the fraction of neutral hydrogen, Ωb is the baryon abundance, and Ts is called the "spin temperature," which defines the relative population of the two spin levels 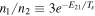 . It can be parameterized in terms of the baryon and photon temperatures, Tb(z) and Tγ(z), and the stimulated Lyα emission (Chen & Miralda-Escudé 2004). In the limit of full Lyα coupling, we take Ts = Tb (Madau et al. 1997). The 21 cm signal is then redshifted until the band of radio frequency today. The EDGES collaboration reported
. It can be parameterized in terms of the baryon and photon temperatures, Tb(z) and Tγ(z), and the stimulated Lyα emission (Chen & Miralda-Escudé 2004). In the limit of full Lyα coupling, we take Ts = Tb (Madau et al. 1997). The 21 cm signal is then redshifted until the band of radio frequency today. The EDGES collaboration reported 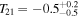 K (99% CL) in a redshift range 13 ≲ z ≲ 22 centered at z ≈ 17 (or a frequency of 78 MHz).
K (99% CL) in a redshift range 13 ≲ z ≲ 22 centered at z ≈ 17 (or a frequency of 78 MHz).
Some aspects of the reported absorption profile are peculiar and need to be explained: the early redshift range with its implications for star formation (Madau 2018; Mirocha & Furlanetto 2019), the flat shape of the profile (Venumadhav et al. 2018), and the unanticipated deep trough. Assuming only standard physical scenarios, the maximum value of the absorption trough would be T21 ≈ −0.2 K; i.e. the measurement is at least twice the standard expectation. Given that T21 depends on the ratio Tγ/Ts, two main explanations are currently discussed to enhance the absorption: (i) an excess of radiation injected from DM annihilations, black holes, or any other astrophysical source (see, e.g., Chianese et al. 2019; Clark et al. 2018; Feng & Holder 2018; Sharma 2018); and (ii) a cooling mechanism of baryons through interactions with DM (see, e.g., Dvorkin et al. 2014; Tashiro et al. 2014; Muñoz et al. 2015; Barkana 2018; Berlin et al. 2018; Slatyer & Wu 2018; Xu et al. 2018). It should also be mentioned that the EDGES findings are being argued to be due to systematics related to residual foregrounds (Hills et al. 2018). Thus, the EDGES observations require confirmation from similar experiments, like SCI-HI (Voytek et al. 2014), LEDA (Bernardi et al. 2016), and SARAS 2 (Singh et al. 2017). Ultimately, the EDGES results open a rich discussion pointing to new physics and novel phenomenological frameworks.
Here we focus on the baryon–DM interaction hypothesis, assuming a velocity-dependent scattering cross section 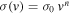 , where
, where 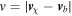 is the relative velocity between two particles.9
We choose to explore two cases of low-energy enhanced interactions, namely n = −4 and −2, which are motivated by models of minicharge and EDM, respectively. Other cases of n have been studied elsewhere (see, e.g., Dvorkin et al. 2014; Slatyer & Wu 2018; Xu et al. 2018).
is the relative velocity between two particles.9
We choose to explore two cases of low-energy enhanced interactions, namely n = −4 and −2, which are motivated by models of minicharge and EDM, respectively. Other cases of n have been studied elsewhere (see, e.g., Dvorkin et al. 2014; Slatyer & Wu 2018; Xu et al. 2018).
The thermal evolution of baryons and DM involves the baryon and DM temperatures, Tb(z) and Tχ(z); the energy transfer between baryons and DM, Qb and Qχ; and the relative bulk velocity Vχb. The full formalism can be read in Dvorkin et al. (2014), Tashiro et al. (2014), or Muñoz et al. (2015); let us just discuss the baryon–DM energy transfer,
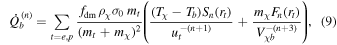
where t refers to the proton or electron, fdm is the fraction of DM interacting with baryons,  is the thermal width of the relative bulk velocity, and
is the thermal width of the relative bulk velocity, and 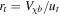 . Notice that the first term subtracts energy from baryons as long as Tχ < Tb. This cooling term is suppressed by the function Sn(rt), where
. Notice that the first term subtracts energy from baryons as long as Tχ < Tb. This cooling term is suppressed by the function Sn(rt), where  and
and 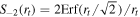 . The second term transforms the mechanical energy into heating to both baryons and DM, where
. The second term transforms the mechanical energy into heating to both baryons and DM, where 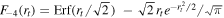 and
and 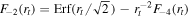 . This term can spoil the cooling mechanism unless the velocity ratio rt (
. This term can spoil the cooling mechanism unless the velocity ratio rt (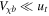 ) or DM mass (
) or DM mass (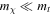 ) is small.
) is small.
The hypothesis of baryon–DM scattering has been extensively studied using CMB and MPS observables (the same observables that we just used to constrain 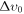 ), which are made of modes that entered the horizon at z ∼ 103–105 (with the Lyα forest, it is possible to probe beyond z ≳ 106). At those early times, the overall effect of baryon–DM interactions would mimic an increase of the baryonic budget; consequently, both the CMB and MPS would become damped on small scales (Chen et al. 2002; Dvorkin et al. 2014). This effect is actually a very good probe for the strength of baryon–DM scattering, and previous studies have reported tight upper limits:
), which are made of modes that entered the horizon at z ∼ 103–105 (with the Lyα forest, it is possible to probe beyond z ≳ 106). At those early times, the overall effect of baryon–DM interactions would mimic an increase of the baryonic budget; consequently, both the CMB and MPS would become damped on small scales (Chen et al. 2002; Dvorkin et al. 2014). This effect is actually a very good probe for the strength of baryon–DM scattering, and previous studies have reported tight upper limits: 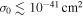 for n = −4 (Boddy et al. 2018; Slatyer & Wu 2018; Xu et al. 2018) and
for n = −4 (Boddy et al. 2018; Slatyer & Wu 2018; Xu et al. 2018) and  for n = −2 (Boddy et al. 2018; Xu et al. 2018).
for n = −2 (Boddy et al. 2018; Xu et al. 2018).
On the other hand, the precise fraction of interacting DM is still in debate (see, e.g., Dolgov et al. 2013; Dolgov & Rudenko 2017). According to constraints derived from the CMB, fdm might be expected below the fractional uncertainty of the baryon energy density (Kovetz et al. 2018). Besides, in order to avoid other astrophysical constraints, a small fdm might be necessary as well (Chuzhoy & Kolb 2009; McDermott et al. 2011). In the following discussion, we consider fdm = {1, 0.1, 0.01} only for exploratory purposes.
Taking into account the smallness of σ0 and fdm from linear cosmology, the baryon–DM interactions would have little impact on the distribution of DM velocities, and their dispersion should evolve as 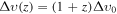 right after photon decoupling. Afterward (z ≲ 103), the low-velocity enhanced scattering (n = −4 or −2) causes a late-time coupling between DM and baryons. Although the noninteracting fraction will preserve an adiabatic dilution (
right after photon decoupling. Afterward (z ≲ 103), the low-velocity enhanced scattering (n = −4 or −2) causes a late-time coupling between DM and baryons. Although the noninteracting fraction will preserve an adiabatic dilution (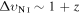 ), the interacting fraction will be heated, and its velocity dispersion
), the interacting fraction will be heated, and its velocity dispersion 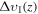 will not follow a linear evolution with z. In fact,
will not follow a linear evolution with z. In fact,  can only be computed numerically after the solution to the heat transfer equations involving Equation (9). Thus, when interactions are effective, the average DM velocity dispersion is
can only be computed numerically after the solution to the heat transfer equations involving Equation (9). Thus, when interactions are effective, the average DM velocity dispersion is
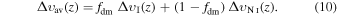
Given that the DM velocity dispersion is constrained directly by the effective amount of matter needed for LSS formation, the constraints found in the previous section should approximately hold, even in the interacting case. Indeed, the upper limit in Equation (7) can be used as an initial condition,

Now, in order to solve the 21 cm thermal dynamics, we can substitute 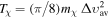 in the thermal width ut, starting the integration at an epoch much before the cosmic dawn (z ∼ 103), and use Equations (7) and (11) to define a set of initial conditions.
in the thermal width ut, starting the integration at an epoch much before the cosmic dawn (z ∼ 103), and use Equations (7) and (11) to define a set of initial conditions.
Let us intuitively discuss the kinematics involved in the 21 cm thermal evolution and heating transfer. We already mentioned below Equation (9) that there is a competition between the cooling mechanism (first term) and the mechanical heating (second term). The most obvious way to enhance the baryon cooling is having a large σ0, albeit possibly conflicting with cosmological bounds. Also obvious is the fact that the colder the DM initially is, the easier it is for it to absorb heat from baryons; this is easily seen in Equation (9) because a smaller thermal width ut enhances the cooling term. Contrarily, the mechanical heating can overcome the cooling mechanism in some cases. For example, particles as heavy as 1–10 GeV would need 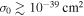 in order to explain the EDGES signal, even in the case of fdm = 1 and zero initial DM velocity dispersion (Barkana 2018), clearly conflicting with cosmological bounds. The mechanical heating can be suppressed, though, if the DM mass is small enough (
in order to explain the EDGES signal, even in the case of fdm = 1 and zero initial DM velocity dispersion (Barkana 2018), clearly conflicting with cosmological bounds. The mechanical heating can be suppressed, though, if the DM mass is small enough (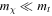 ) and/or the velocity ratio rt is small (
) and/or the velocity ratio rt is small (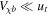 ). The latter has also been identified as a necessary condition to maintain linearity in the perturbative Boltzmann equations (see, e.g., Boddy & Gluscevic 2018; Boddy et al. 2018; Kovetz et al. 2018; Slatyer & Wu 2018).
). The latter has also been identified as a necessary condition to maintain linearity in the perturbative Boltzmann equations (see, e.g., Boddy & Gluscevic 2018; Boddy et al. 2018; Kovetz et al. 2018; Slatyer & Wu 2018).
The DM mass is a very interesting parameter in this framework. Given that the absorbed heat is distributed among the number of interacting DM particles, the cooling mechanism seems to be easier if the DM mass is small. In other words, when the DM is the lighter, the transferred energy is spread out over more particles, which could be understood as a more efficient thermal reservoir than in the heavier case.
We also identify a couple of differences between the two types of scattering. (i) For n = −4, the electron–DM interaction is only relevant if the DM particles are not cold; otherwise, σ0 is dominated by proton–DM interactions. (ii) On the other hand, for n = −2, the scattering is electron-dominated for 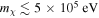 (even for cold DM particles); above that mass, the interaction is proton-dominated.
(even for cold DM particles); above that mass, the interaction is proton-dominated.
Now we can proceed to fit the 21 cm temperature appearing in Equation (8) to the EDGES measurement. In practice, for each pair of 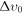 , mχ fixed values, we solve for σ0 to recover T21(z = 17) ≈ −0.5 K. Figure 3 displays the resulting allowed regions for σ0 and mχ marginalized over Δυ0 for n = −4 and −2 and the fractions fdm = 1 and 0.01. Notice that if the initial thermal width ut is large, it will suppress the cooling term in Equation (9); such a suppression can only be compensated by σ0, requiring stronger baryon–DM interactions. The larger values of σ0 in Figure 3 are clearly in conflict with typical cosmological bounds.10
Indeed, with a tighter bound on Δυ0 resulting from small-scale LSS data like, e.g., the Lyα forest, the allowed space for σ0 would shrink below the current cosmological bounds. For masses above 0.1 MeV, the explanation of the EDGES measurement requires heavy DM particles to initially be very cold. But lighter DM particles are much less restricted in their velocity dispersion initial conditions, which is due to the aforementioned better cooling efficiency of light DM particles.
, mχ fixed values, we solve for σ0 to recover T21(z = 17) ≈ −0.5 K. Figure 3 displays the resulting allowed regions for σ0 and mχ marginalized over Δυ0 for n = −4 and −2 and the fractions fdm = 1 and 0.01. Notice that if the initial thermal width ut is large, it will suppress the cooling term in Equation (9); such a suppression can only be compensated by σ0, requiring stronger baryon–DM interactions. The larger values of σ0 in Figure 3 are clearly in conflict with typical cosmological bounds.10
Indeed, with a tighter bound on Δυ0 resulting from small-scale LSS data like, e.g., the Lyα forest, the allowed space for σ0 would shrink below the current cosmological bounds. For masses above 0.1 MeV, the explanation of the EDGES measurement requires heavy DM particles to initially be very cold. But lighter DM particles are much less restricted in their velocity dispersion initial conditions, which is due to the aforementioned better cooling efficiency of light DM particles.
Figure 3. Constraints on the baryon–DM scattering cross section required to explain the EDGES signal, reported in terms of the mass and marginalized over 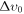 . The blue (green) region represents the 99% CL for
. The blue (green) region represents the 99% CL for  (fdm = 0.01). Each solid line represents the Planck upper bounds on the cross section from Boddy et al. (2018 and Slatyer & Wu (2018); blue for fdm = 1.0 and green for fdm = 0.01); dashed lines are an extrapolation to smaller DM masses.
(fdm = 0.01). Each solid line represents the Planck upper bounds on the cross section from Boddy et al. (2018 and Slatyer & Wu (2018); blue for fdm = 1.0 and green for fdm = 0.01); dashed lines are an extrapolation to smaller DM masses.
Download figure:
Standard image High-resolution image5. Electromagnetic Properties of DM?
In this section, we discus the physical motivation for the n = −4 and −2 scattering cases, relating them to the electric minicharge  and EDM
and EDM  of DM, respectively.
of DM, respectively.
5.1. Minicharge
The possible existence of new particles endowed with a small electric charge qχ =  e (where e is the electron charge and
e (where e is the electron charge and  ≪ 1) is well motivated from simple extensions of the SM that include a hidden sector with a U'(1) unbroken gauge symmetry (Holdom 1986; Foot et al. 1990). The small effective charge is a by-product of the kinetic mixing between hidden photons associated with U'(1) and ordinary photons. Then, fermions in the hidden sector charged under U'(1) can couple to ordinary photons via qχ. If there were light-charged scalars in the hidden Higgs sector, they would also acquire a tiny charge qχ due to the photon mixing (Melchiorri et al. 2007; Ahlers et al. 2008; An et al. 2013). In some models, even neutrinos are explicitly allowed to acquire a small charge (Foot et al. 1990; Vinyoles & Vogel 2016). It turns out to be quite intuitive to think of minicharged particles (MCPs) to account for at least a fraction of the DM (Goldberg & Hall 1986). Indeed, MCPs are often quoted within the group of WISP DM candidates (Jaeckel & Ringwald 2010; Ringwald 2012), including dark photons, majorons, axions, and axion-like particles.
≪ 1) is well motivated from simple extensions of the SM that include a hidden sector with a U'(1) unbroken gauge symmetry (Holdom 1986; Foot et al. 1990). The small effective charge is a by-product of the kinetic mixing between hidden photons associated with U'(1) and ordinary photons. Then, fermions in the hidden sector charged under U'(1) can couple to ordinary photons via qχ. If there were light-charged scalars in the hidden Higgs sector, they would also acquire a tiny charge qχ due to the photon mixing (Melchiorri et al. 2007; Ahlers et al. 2008; An et al. 2013). In some models, even neutrinos are explicitly allowed to acquire a small charge (Foot et al. 1990; Vinyoles & Vogel 2016). It turns out to be quite intuitive to think of minicharged particles (MCPs) to account for at least a fraction of the DM (Goldberg & Hall 1986). Indeed, MCPs are often quoted within the group of WISP DM candidates (Jaeckel & Ringwald 2010; Ringwald 2012), including dark photons, majorons, axions, and axion-like particles.
The long-standing question about MCPs has led to several laboratory searches, like the experiments at the SLAC National Accelerator Laboratory, uniquely designed to detect MCPs (Prinz et al. 1998; Badertscher et al. 2007; Gninenko et al. 2007; Batell et al. 2014) that have set an upper bound  ≲ 10−5 in the 0.1–100 MeV mass range. Collider precision tests have set bounds going down to
≲ 10−5 in the 0.1–100 MeV mass range. Collider precision tests have set bounds going down to  ≲ 5 × 10−4 (Davidson et al. 2000) for masses below 100 keV. Meanwhile, astrophysical and cosmological environments represent advantageous laboratories, as many of them are sensitive to the effects of MCPs. For instance, Big Bang nucleosynthesis (BBN) sets the condition
≲ 5 × 10−4 (Davidson et al. 2000) for masses below 100 keV. Meanwhile, astrophysical and cosmological environments represent advantageous laboratories, as many of them are sensitive to the effects of MCPs. For instance, Big Bang nucleosynthesis (BBN) sets the condition  ≲ 10−8 (Mohapatra & Rothstein 1990) in order to prevent late thermalization of ≲MeV particles. Otherwise, DM would contribute with extra relativistic dof, which are tightly constrained to Neff = 2.94 ± 0.38 (Cyburt et al. 2016). If one counts the extra relativistic dof due to the hidden photons, the CMB bounds on Neff also place constraints on the MCP parameter space (see, e.g., Vinyoles & Vogel 2016; Barkana et al. 2018).
≲ 10−8 (Mohapatra & Rothstein 1990) in order to prevent late thermalization of ≲MeV particles. Otherwise, DM would contribute with extra relativistic dof, which are tightly constrained to Neff = 2.94 ± 0.38 (Cyburt et al. 2016). If one counts the extra relativistic dof due to the hidden photons, the CMB bounds on Neff also place constraints on the MCP parameter space (see, e.g., Vinyoles & Vogel 2016; Barkana et al. 2018).
The strongest bounds on minicharge come from the energy-loss argument, alluding to the escape of these particles from the cores of stars (Raffelt 1996). Excitations of the dense electron–proton plasma (also called plasmons) can decay into MCPs; if the charge is low enough ( ≲ 10−8; Davidson et al. 2000), they propagate freely through the plasma and escape from the star (Vinyoles & Vogel 2016). The dissipation of energy should modify the usual stellar evolution, thus limiting the plasmon decay rate into MCPs and hence constraining
≲ 10−8; Davidson et al. 2000), they propagate freely through the plasma and escape from the star (Vinyoles & Vogel 2016). The dissipation of energy should modify the usual stellar evolution, thus limiting the plasmon decay rate into MCPs and hence constraining  . Combining studies of white dwarfs (WDs), red giants (RGs), SN 1987-A (SN 87A), and the Sun (among others) indicates that
. Combining studies of white dwarfs (WDs), red giants (RGs), SN 1987-A (SN 87A), and the Sun (among others) indicates that  ≲ 2 × 10−14 (Davidson et al. 2000; Vinyoles & Vogel 2016; Chang et al. 2018; see also Figure 4).
≲ 2 × 10−14 (Davidson et al. 2000; Vinyoles & Vogel 2016; Chang et al. 2018; see also Figure 4).
Figure 4. Constraints on the DM minicharge required to explain the EDGES signal. The blue (green) region represents our 99% CL constraints for fdm = 1 (fdm = 0.01) that are consistent with our bound (Equation (7)) on the DM velocity dispersion. Bounds on MCPs from the early universe and stellar physics are also shown (see text for references). The CMB–Neff bound applies only to the model that explicitly includes the hidden photon relativistic dof.
Download figure:
Standard image High-resolution imageIn the DM mass range of this work (10−3–109 eV), the DM particle number density is always comparable to or much larger than baryons. Then, we should consider the cross section due to a baryon propagating in an MCP plasma (McDermott et al. 2011),
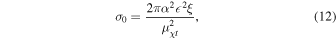
where α is the fine-structure constant and 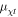 is the reduced mass between the DM and the baryon (proton or electron). The Debye logarithm
is the reduced mass between the DM and the baryon (proton or electron). The Debye logarithm 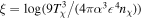 , which regulates the screening of the interaction by the plasma, can be approximated in this case to
, which regulates the screening of the interaction by the plasma, can be approximated in this case to 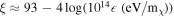 . Given that MCPs cannot interact with neutral atoms, the energy transfer in Equation (9) gets suppressed by the fraction of free electrons.
. Given that MCPs cannot interact with neutral atoms, the energy transfer in Equation (9) gets suppressed by the fraction of free electrons.
We can now obtain minicharge bounds by inserting Equation (12) into the heat transfer Equation (9); this is depicted in Figure 4. Notice that in order to simultaneously explain the EDGES signal and avoid stellar bounds, the DM mass needs to be toward the ultralight regime. From the nonexcluded mχ– window, some bounds on the DM minicharge are listed in Table 2 according to three values of fdm. Notice once again that a tighter bound on Δυ0 would result in a reduced allowed space for
window, some bounds on the DM minicharge are listed in Table 2 according to three values of fdm. Notice once again that a tighter bound on Δυ0 would result in a reduced allowed space for  .
.
Table 2. Bounds on the DM Minicharge
| fdm | mχ |  |
|---|---|---|
| 1 | 10−3–2 eV |
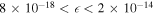
|
| 0.1 |
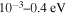
|

|
| 0.01 |
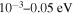
|
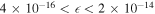
|
Note. Bounds on  are directly read from Figure 4.
are directly read from Figure 4.
Download table as: ASCIITypeset image
Incidentally, notice that the scattering due to MCPs is dominantly incoherent for our studied range of masses. This is due to the smallness of  , causing the MCPs' mean free path
, causing the MCPs' mean free path 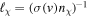 to be extremely large compared to the energy-exchange length
to be extremely large compared to the energy-exchange length 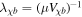 . Despite the apparently high densities at lower masses (e.g., for z = 20 and mχ = 1 eV,
. Despite the apparently high densities at lower masses (e.g., for z = 20 and mχ = 1 eV, 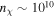 cm−3), the smallness of
cm−3), the smallness of  makes the MCPs a rarefied plasma. This might not be the case for ultralight DM candidates. A minicharge as small as
makes the MCPs a rarefied plasma. This might not be the case for ultralight DM candidates. A minicharge as small as  ∼ 10−14 will be enough to cause (
∼ 10−14 will be enough to cause (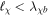 ) a scattering dominantly coherent for
) a scattering dominantly coherent for 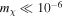 eV.
eV.
5.2. EDM
Following the same spirit of MCPs, a type of neutral DM possessing an EDM 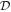 has been targeted for direct detection (Pospelov & ter Veldhuis 2000; Sigurdson et al. 2004, 2006).11
These particles can only be Dirac fermions in order to have a permanent dipole moment. It is customary to report
has been targeted for direct detection (Pospelov & ter Veldhuis 2000; Sigurdson et al. 2004, 2006).11
These particles can only be Dirac fermions in order to have a permanent dipole moment. It is customary to report 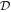 in units of the Bohr magneton,
in units of the Bohr magneton, 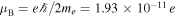 cm.
cm.
The BBN sets an upper bound, 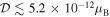 , in order to avoid late thermalization of particles below a few MeV (Sigurdson et al. 2004). In the sub-GeV mass range, collider physics is the most sensitive probe to DM EDM through radiative corrections to the W boson mass, which sets a mass-independent upper limit at
, in order to avoid late thermalization of particles below a few MeV (Sigurdson et al. 2004). In the sub-GeV mass range, collider physics is the most sensitive probe to DM EDM through radiative corrections to the W boson mass, which sets a mass-independent upper limit at 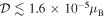 , and from perturbative constraints from corrections to Z-pole observables, requiring that
, and from perturbative constraints from corrections to Z-pole observables, requiring that  (Sigurdson et al. 2004). Stellar physics constrain the neutrino magnetic dipole moment (MDM) from the energy-loss argument discussed above. These constraints also apply to DM particles coupling to photons through an EDM. Accordingly, the most stringent astrophysical limits correspond to the Sun, WDs, RGs, and SN 87A, implying
(Sigurdson et al. 2004). Stellar physics constrain the neutrino magnetic dipole moment (MDM) from the energy-loss argument discussed above. These constraints also apply to DM particles coupling to photons through an EDM. Accordingly, the most stringent astrophysical limits correspond to the Sun, WDs, RGs, and SN 87A, implying  (Bertolami 2014; Kadota & Silk 2014; Arceo-Díaz et al. 2015; Cañas et al. 2016).
(Bertolami 2014; Kadota & Silk 2014; Arceo-Díaz et al. 2015; Cañas et al. 2016).
Our bounds on σ0 computed with a v−2 dependence (as shown in Figure 3) can be translated to 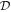 , according to Sigurdson et al. (2004),
, according to Sigurdson et al. (2004),

From the results depicted in Figure 5, we can see that the EDM needed to explain the EDGES measurement in the mass range 10−3–109 eV is already discarded by the BBN constraints and the measurements of the W boson mass in colliders.
Figure 5. Constraints on the DM EDM required to explain the EDGES signal, along with the region already excluded by BBN and collider experiments. The blue (green) region represents the 99% CL region consistent with our constraints on the DM velocity dispersion for 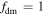 (
(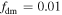 ).
).
Download figure:
Standard image High-resolution imageAs discussed above in the case of MCPs, the scattering through an EDM is also dominated by incoherent scattering in the mass range 10−3–109 eV. For example, if 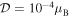 , the scattering would be coherent (
, the scattering would be coherent (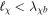 ) for
) for 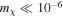 eV. For an EDM as small as
eV. For an EDM as small as 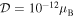 , the scale of coherent scattering is pushed down to
, the scale of coherent scattering is pushed down to 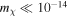 eV.
eV.
6. Conclusions
While the mass is quite an unknown aspect of DM, its velocity dispersion is a physical property much less studied. It is not uncommon to think that the DM relic velocity is either necessarily zero (assuming cold DM) or thermally suppressed by the particle mass (in warm DM models), as in Equations (1) and (2). Nevertheless, as we have reviewed, there might be plenty of nonthermal mechanisms that would cause finite velocity dispersions, to some degree disentangling velocity and mass. Here we have constrained a wide region of the mχ–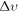 diagram (Figure 2) by means of the linear regime of matter perturbations and using current CMB and LSS data. Our analysis provides useful upper limits to the DM velocity dispersion, listed in Table 1 and summarized in Equation (7). In general, we have shown that DM particles can be considered as warm or cold DM depending on their actual velocity dispersion, irrespective of their mass.
diagram (Figure 2) by means of the linear regime of matter perturbations and using current CMB and LSS data. Our analysis provides useful upper limits to the DM velocity dispersion, listed in Table 1 and summarized in Equation (7). In general, we have shown that DM particles can be considered as warm or cold DM depending on their actual velocity dispersion, irrespective of their mass.
As expected, active neutrinos and thermal axions (hot DM) are ruled out as the main source of DM. Thermal majorons are found to be barely allowed by our constraints, suggesting the need for further scrutiny with CMB and LSS data and possibly accounting for their nonthermal corrections. Candidates for thermal DM are allowed above ∼100 eV by our constraints, while they are discarded for mχ ≲ 40 eV, even after considering nonthermal corrections. The RP sterile neutrinos and other nonthermal DM candidates are well inside our bounds. Very light (≪1 keV) DM particles are allowed by our constraints as long as their velocity dispersion concurs with our bound in Equation (7). This motivates a deeper study of nonthermal production mechanisms like those briefly discussed in Section 2. Heavy thermal candidates are well below our velocity constraints.
Our bound (Equation (7)) on the DM velocity dispersion is mainly limited by the maximum wavenumber (0.2 h Mpc−1) contained in the SDSS DR4 LRG data. This motivates further studies using LSS data at smaller scales, like those from the Lyα forest, which can extend our analysis down to 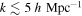 and improve our constraints by at least an order of magnitude.
and improve our constraints by at least an order of magnitude.
The DM velocity dispersion is a key ingredient of the 21 cm dynamics at the epoch of the cosmic dawn. If the anomaly in the absorption profile measured by EDGES is to be explained by a baryon–DM interaction, the T21 signal by itself is not enough to constrain both the DM relic velocity and the baryon–DM scattering cross section. Hence, it is of great importance to investigate 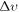 using independent techniques and sets of data.
using independent techniques and sets of data.
In order to overcome the highest allowed velocities and henceforth ensure efficient baryon cooling, the values of σ0 would need to be accordingly larger (as depicted in Figure 3). However, the largest σ0 values are in conflict with previous bounds (Boddy et al. 2018; Slatyer & Wu 2018; Xu et al. 2018) obtained from CMB and LSS data. This means that if DM particles are very heavy (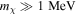 ), they ought to initially be really cold in order to explain the EDGES observation. If DM particles are very light (
), they ought to initially be really cold in order to explain the EDGES observation. If DM particles are very light (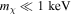 ), they do not seem to have tight restrictions on their initial velocities—other than Equation (7)—in order to explain both early and late cosmological data. Yet we speculate that such very light DM scenarios would, in turn, need a very early cooling mechanism (like those discussed in Section 2) in order to attain velocities much smaller than thermal candidates.
), they do not seem to have tight restrictions on their initial velocities—other than Equation (7)—in order to explain both early and late cosmological data. Yet we speculate that such very light DM scenarios would, in turn, need a very early cooling mechanism (like those discussed in Section 2) in order to attain velocities much smaller than thermal candidates.
We conclude that the 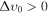 allowed values found after our analysis can surely play a major role in the phenomenology of baryon cooling. Once again, this motivates further studies with Lyα forest or other small-scale LSS data, which could tighten the allowed parameter space for the baryon–DM scattering cross section and minicharge (see Figures 3 and 4).
allowed values found after our analysis can surely play a major role in the phenomenology of baryon cooling. Once again, this motivates further studies with Lyα forest or other small-scale LSS data, which could tighten the allowed parameter space for the baryon–DM scattering cross section and minicharge (see Figures 3 and 4).
Assuming that the n = −4 and −2 types of scattering are due to, respectively, MCPs and EDMs, our constraints on σ0 translate to novel bounding areas for  and
and 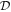 , which are modified by our constraints on Δυ0. This effect is interesting in general for direct detection experiments at the low-energy end, whose typical targets are WISPs (Jaeckel & Ringwald 2010; Ringwald 2012). In this direction of research, a more complete and detailed sampling of the (mχ, Δυ0, σ0) parameter space would be needed. In particular, the mass parameter space should be explored considering that the interacting and noninteracting DM fractions may be made of particles with different masses. This characterization will involve explicitly collisional terms in the baryon and DM Boltzmann equations and a Boltzmann hierarchy of differential equations. Clearly, the former study would be very interesting and represents one way to improve our analysis.
, which are modified by our constraints on Δυ0. This effect is interesting in general for direct detection experiments at the low-energy end, whose typical targets are WISPs (Jaeckel & Ringwald 2010; Ringwald 2012). In this direction of research, a more complete and detailed sampling of the (mχ, Δυ0, σ0) parameter space would be needed. In particular, the mass parameter space should be explored considering that the interacting and noninteracting DM fractions may be made of particles with different masses. This characterization will involve explicitly collisional terms in the baryon and DM Boltzmann equations and a Boltzmann hierarchy of differential equations. Clearly, the former study would be very interesting and represents one way to improve our analysis.
On a side note, we briefly mentioned the mass scale of incoherent/coherent scattering for MCPs and EDMs. We lastly say that in the latter case, the continuum nature of DM ought to be taken into account in close similarity to scale-invariant scenarios (Katz et al. 2016). Moreover, the associated multibody interaction might imply a scattering driven by higher-order multipoles, possibly the anapole, quadrupole, or DM polarizability (Pospelov & ter Veldhuis 2000; Ovanesyan & Vecchi 2015).
The authors thankfully acknowledge the computer resources provided by the Laboratorio Nacional de Supercómputo del Sureste de México, CONACYT network of national laboratories. This project was possible owing to partial support from CONACYT research grants 237004, 490769, F.C. 2016/1848, and FORDECYT. We also thank Tracy Slatyer, Cora Dvorkin, R.E. Sanmiguel, and J.B. Muñoz for interesting discussions. We especially want to thank the anonymous referee for a critical review that led to a significant improvement of our paper.
Footnotes
- 5
On local scales, DM dynamics is influenced by gravitational infall, violent relaxation, and astrophysical feedback effects so that the DM velocity dispersion becomes much different than the primordial value. For example, in the Milky Way halo, the velocity dispersion distribution deviates from the isotropic case, attaining, e.g., radial velocity dispersion values of ∼200 km s−1 at the maximum (Bird et al. 2019).
- 6
Commonly, BECs are referred to as nonthermal states, though their physical origin is obviously thermal.
- 7
Elastic scattering with SM species is usually responsible for keeping DM particles in thermal equilibrium. In some models, kinetic decoupling might be assumed to occur at xd ≈ 1 (Lesgourgues et al. 2013). On the other hand, WIMP coannihilation numerical studies suggest that their freeze-out point is xf = m/Tf ≈ 20−30 (Roszkowski et al. 2018). In general, xf and xd are separate unknown parameters, but the uncertainty is one-sided because the freeze-out should typically precede the kinetic decoupling.
- 8
Notice that these constraints are still subject to uncertainties on the thermal evolution of the intergalactic medium.
- 9
It is also customary to use a parameter σ1 that relates to σ0 as
![${\sigma }_{0}={([1\mathrm{km}{{\rm{s}}}^{-1}]/{\rm{c}})}^{4}\,{\sigma }_{1}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) .
. - 10
But recall that current cosmological bounds have been mainly focused on DM masses above MeV.
- 11
The MDMs
 have been experimentally targeted as well. Here we do not consider MDMs because they produce a velocity-independent scattering (n = 0) with baryons (see, e.g., Sigurdson et al. 2006).
have been experimentally targeted as well. Here we do not consider MDMs because they produce a velocity-independent scattering (n = 0) with baryons (see, e.g., Sigurdson et al. 2006).








![${\sigma }_{0}={([1\mathrm{km}{{\rm{s}}}^{-1}]/{\rm{c}})}^{4}\,{\sigma }_{1}$](https://content.cld.iop.org/journals/0004-637X/894/1/40/revision1/apjab67d0ieqn74.gif)