Working memory (WM) is a limited capacity system of cognitive processes that can maintain and manipulate temporarily activated mental representations required for complex cognition (Baddeley & Hitch, 1974). WM plays an important role in language comprehension, reasoning, planning, and problem-solving, making it a core component of numerous general theories and models of cognition (Anderson & Lebiere, 1998; Cowan, 1995; Oberauer, 2002, 2003, 2019).

While all humans have a WM, individual differences in the capacity to hold and manipulate information in WM vary. Over the years, research has found that individual differences in WM capacity (WMC) are associated with overall cognitive ability (Kane et al., 2001; Kovacs & Conway, 2016) and serve as a strong predictor of a broad range of outcomes, including academic achievement (Alloway & Alloway, 2010; Gathercole et al., 2003), reading comprehension (Engle et al., 1992; Daneman & Carpenter, 1980; McVay & Kane, 2012), mathematical ability (Ramirez et al., 2013; Turner & Engle, 1989, and multi-tasking (Redick et al., 2016; 2012), among others. For this reason, WMC is often measured in psychological research.

Multiple cognitive tasks to measure WMC are readily available and have become popular tools to assess individual differences in cognitive ability (Foster et al., 2015). For example, complex span tasks are the most commonly used measures of WMC; they require both simultaneously storing and processing information, thus assessing both key dimensions of WMC (Conway et al., 2005). While tasks of WMC, such as complex span tasks, were originally designed to assess domain-general WM by averaging responses across multiple domain-specific tasks, it has become increasingly common for researchers to use only one task to measure WMC when resources are limited (Foster et al., 2015). However, to ensure that domain-general WM is effectively measured, it is important to understand whether there are critical differences among types of complex span task, as well as in the degree of domain generality that the tasks assess individually.

Psychometric studies examining complex span tasks have focused on using factor analysis approaches to explore the degree of common variance that is captured by a latent construct (i.e., WMC). This extensive psychometric work has shown that complex span tasks overall assess domain-general WM. However, recent research has found that some of the complex span tasks present domain-specific differences (Foster et al., 2015; Draheim et al., 2018). To examine where these variations arise and how they might affect the interpretation of complex span scores for domain-general WM, item response theory (IRT) can be used as a technique to examine each item of the tasks to produce a more accurate depiction of their underlying traits. IRT can estimate subject scores for a given item in a test, providing more information about each test item. This can help estimate parameters such as subject’s ability level, item difficulty, and discrimination without considering the items as a whole, but rather treating them independently, as opposed to traditional methods (Embretson, 1996). Further, compared to classic test theory, IRT relies on different statistical assumptions that may reflect different theoretical implications in psychometric and individual differences research. For example, IRT models assume non-linear associations between the items and the estimated latent construct. In addition, measurement errors vary across trait levels, while in classic test theory, the errors of measurement are constant for all scores. Finally, compared to total raw scores, trait estimates from IRT are optimal scales of individual differences and have better scaling properties (Reise et al., 2005).

Complex span tasks

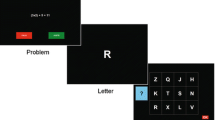
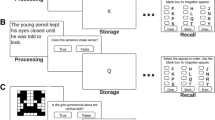
The most commonly used set of tasks to measure WMC are known as “complex span” (e.g., reading span, operation span, symmetry span, and rotation span; see Conway et al., 2005). Complex span tasks are widely used because they consistently exhibit good reliability and strong predictive validity (Conway et al., 2005), thus constituting a solid theoretical measurement of working memory as a multicomponent system based on the original work of Baddeley & Hitch, 1974). The tasks originated in individual differences research, mainly in the field of cognitive psychology, but they have become widespread in other areas of psychology as well, including social, industrial/organizational, developmental, education, and clinical psychology (e.g., Allen et al., 2015; Christopher & MacDonald, 2005; Redick, Heitz, & Engle, 2007). Complex span tasks require storage and simultaneous processing of information (sometimes referred to as storage & processing tasks or maintenance & manipulation tasks) and were designed as an alternative to simple span tasks, such as digit span, which only require storage of information. On the one hand, in a simple span task, a list of stimuli (e.g., digits) is presented, and at the end of the list, the subject is prompted to recall the stimuli in the serial order in which they were presented. In contrast, in a complex span task, the presentation of each stimulus is preceded by a resource-demanding secondary task (the processing component), such as solving a math problem. For example, in the Operation span, subjects are presented with a list of interleaved letters (i.e., stimuli) shown one at a time on the screen while solving simple math equations (i.e., processing component) (e.g., Is (2 x 3) -1 = 5?). The subject is instructed to remember the letters for later recall and verify each equation by responding true or false. After each list of letters and math equations (i.e., item), subjects are prompted to recall the letters in serial order (see Fig. 1). The number of letters accurately recalled is considered to be an indicator of WMC. In other words, WMC is the amount of information that can be maintained in the face of concurrent processing.

Fig. 1
figure 1

Example of complex span tasks. In both tasks, subjects are first shown a processing stimulus (i.e., solving a mathematical problem or deciding whether a pattern is symmetrical), followed by a to-be-remembered storage stimulus (i.e., a letter or the location of a red square in a grid). At the end of a list of storage and processing stimuli (i.e., item), subjects must enter all the to-be-remembered storage stimuli they were presented in order of appearance

Full size image

Thus, in complex span tasks, an “item” is defined as the entire set of to-be-remembered “storage” stimuli and the interleaved “processing” stimuli. In other words, a list of letters and a list of equations in the operation span form an item. In addition, in a given complex span task, the storage and processing stimuli belong to the same domain. That is, in verbal complex span tasks, both the storage and processing stimuli are verbal, while in spatial complex span tasks, both the storage and processing stimuli are spatial. Complex span tasks traditionally consist of three blocksFootnote 1, with item sizes ranging from 2 to 5 (visuospatial) or 3 to 7 (verbal) storage and processing stimuli (see Appendix for further details). There are several procedures to score responses to complex span tasks, but the most common is the partial-credit load (PCL) method (Conway et al., 2005). PCL is the sum of correctly recalled storage stimuli from all items, regardless of whether each storage stimulus in a to-be-remembered item is perfectly recalled or not. Therefore, total scores are weighted based on item size (i.e., longer items contribute more to the total score than shorter ones). For each item, the maximum score equals the number of storage stimuli presented in that item while the minimum score is 0. For example, in operation span, subjects complete 12 items of 2-5 to-be-recalled storage stimuli each. Following this, a person could obtain the following scores: 1 + .5 + 1 + 1+ 1+ 1+ .75+ .5 + .75 + .8 + .8 + .8, that is, 1 for an entirely correctly recalled item and partial credit for an item that was not fully recalled (instead of a 0). Thus, this person’s span score would be 9.9/12 or .83. This scoring method has been shown to be a reliable measure of WMC (Conway et al., 2005).

Domain-general ability

As mentioned, complex span tasks are thought to measure primarily the domain-general component of WM (Harrison et al., 2014). This is supported by individual differences research showing that WMC is largely a domain-general cognitive ability (Engle, 2002; Engle & Kane, 2004; Engle, Nations, & Cantor, 1990; Harrison et al., 2014, Cantor et al., 1991). For example, in an influential study on the domain-generality of WMC, Kane et al. (2004) examined the relationship between verbal and visuospatial complex span tasks, verbal and visuospatial simple span tasks, and tests of fluid intelligence. The researchers found that complex span tasks loaded on a single factor, whereas the simple span tasks loaded on two separate factors (verbal and spatial), and a latent factor reflecting the complex span tasks was a strong predictor of general fluid intelligence, consistent with previous studies (Engle et al., 1999a; Conway et al., 2003; Colom et al., 2005; Kyllonen & Christal, 1990; Unsworth et al., 2014; for a review see Kane et al., 2005). These findings support the view that the shared variance between complex span tasks and fluid intelligence reflects a domain-general cognitive ability. Further evidence for the domain-generality of complex spans comes from neuroimaging studies of WM. Chein et al. (2011) conducted an fMRI experiment to examine task-related neural activity as subjects performed verbal and spatial complex and simple span tasks. The results of the study revealed greater activity in the fronto-parietal network during verbal complex span compared to simple span and during spatial complex span compared to simple span. In addition, the researchers also found significant overlap in neural activity associated with complex verbal and complex spatial span. Overall, the findings suggest that both types of complex span tasks tap general processes.

The evidence reported above suggests that complex span tasks are more representative of domain-general WM than simple span tasks (Conway et al., 2002; Cowan et al., 2005; Kane, Hambrick, Conway, 2005; Engle, Kane, & Tuholski, 1999a,b; Engle, Tuholski, Laughlin, & Conway, 1999c; Unsworth, Heitz, & Engle, 2005). However, it is important to highlight evidence that shows the contrary. More recently, Wilhelm et al. (2013) tested different families of working memory tasks to understand whether these tasks shared the same domain-general variance. Their findings show that working memory may not be completely reflective of a domain-general component. Rather, working memory also reflects bindings; namely, the ability to update and maintain information. Other evidence has also shown that working memory may reflect storage as opposed to updating or other domain-general processes as originally thought (Frischkorn et al., 2022). Taken together, these findings challenge the view that working memory is a purely domain-general ability. Regardless of the mixed evidence reviewed above, most of these psychometric studies utilize factor analysis approaches to examine variance shared by complex span tasks. Item response theory (IRT) can instead examine whether individual items in the tasks (in which stimuli vary) present variable response patterns that cannot otherwise be observed. To establish that all complex span tasks assess domain-general WM as observed in factor analysis studies, homogeneity across tasks response patterns should be observed.

Domain-specific ability

The available evidence indicates that complex span tasks largely reflect a domain-general ability while simple span tasks are more domain-specific. However, research has also shown some differences in complex span task performance across domains. For example, subjects tend to perform better on verbal tasks compared to visuospatial tasks. Specifically, when examining performance at the item-level, research has shown that responses to operation span tend to exhibit higher accuracy in later blocks compared to earlier blocks (Draheim, Harrison, Embretson & Engle, 2018), which may reflect a practice or strategy effect. In fact, results from Kane et al. (2004) showed that a WMC factor based on visuospatial complex span tasks was a stronger predictor of general fluid intelligence than a WMC factor based on verbal complex span tasks. This raises the concern that verbal complex span tasks may reflect verbal ability to a greater extent than visuospatial complex span tasks reflect visuospatial ability. It is worth noting that the general view that WMC (in particular verbal tasks) reflects domain-specific abilities to a greater extent is part of a larger debate; some scholars support a view in which working memory is thought to be driven by multiple specialized domain-specific processes (Vergauwe et al., 2022; Colheart, 1999; Morey et al., 2019), while other researchers instead propose that working memory is influenced by single domain-general resources (Cowan, 1999).

There is also research indicating that there are developmental differences in the relationship between general and domain-specific WM in young children. For example, Alloway, Gathercole, & Pickering (2006) found that young children use more executive resources, such as controlled attention when completing visuospatial tasks than when completing verbal tasks, suggesting that young children draw on previously known information to complete verbal tasks. Similarly, Demir, Prado and Booth (2014) found that children with higher verbal WM tended to present activity in the left temporal cortex, whereas higher spatial ability was related to activity in the right parietal cortex when completing the same arithmetic task. Finally, Mackintosh and Bennett (2003) found that verbal WM and spatial WM formed two related but separate factors using confirmatory factor analysis, leading the researchers to conclude that WM is likely in part domain-specific.

In addition to evidence from developmental research, there seem to be domain-specific variations in WM training paradigms. Specifically, some studies have found that subjects present training-induced changes only when the training task and the transfer task are both verbal, as opposed to nonverbal tasks (Gathercole, Dunning, Holmes, & Norris, 2019; Holmes, Woolgar, Hampshire, & Gathercole, 2019). However, other studies have shown that visuospatial skills can be trained (Foster et al., 2017; Uttal et al., 2013), suggesting that perhaps verbal and visuospatial WM require different approaches to observe training gains. It is unclear where such differences between verbal and spatial tasks originate, but it is possible that they are related to the fact that verbal tasks may facilitate the use of rehearsal or other practice strategies (Turley-Ames & Whitfield, 2003).

In this context, item response theory (IRT) is a largely unexplored approach in the area of working memory that could help understand differences between verbal and spatial complex span tasks. IRT models, especially those with confirmatory parameters, can represent cognitive theory variables and describe corresponding characteristics of the items (Embretson & McCollam, 2000a, 2000b). Recent research shows that item-level responses can help explain variations among different types of complex span tasks (Draheim et al., 2018), indicating that observing item-level trends can be informative of the processes used to respond to different types of tasks.

Item response theory

Item response theory (IRT) is a psychometric assessment and modeling technique that estimates a respondent’s standing on underlying attributes, or latent traits, by creating a corresponding psychometric estimation based on maximized information from individual items in a test (Brown & Croudace, 2015), independently of the test. Both IRT and traditional methods like classical test theory are used to develop and implement multi-item scales to assess unobservable constructs or latent variables. For this, IRT estimates the probability that a subject’s response to a given item falls within a specific category, while in classical test theory, the focus is to measure a person’s average response levels (Embretson & Reise, 2013). Thus, while classical test theory primarily estimates subjects’ scores for an entire test, IRT incorporates more information about each individual item of a test to produce a more accurate depiction of the target traits, allowing a clearer investigation of a subject’s ability level, item difficulty, and discrimination. As opposed to classical test theory, IRT items are treated independently from one another. For example, the difficulty of an item in IRT is relative to the ability level of an individual, thus the test score of a population in IRT are a mean value of the individual’s values, whereas in classical test theory the single value applies to all trait levels. Similarly, in classical test theory, comparing across tests scores requires having equal tests forms (i.e., parallelism), while in IRT comparing across tests forms is acceptable when test difficulty varies across individuals. In terms of parameter estimation, both classical test theory and IRT estimate difficulty and discrimination, but they do so in different ways. Classical test theory often calculates difficulty as a measure of proportion of correct responses and calculates discrimination as point-biserial correlations. In IRT, difficulty (or b) is estimated as the probability of responding correctly to an item based on a subject’s ability level and discrimination (or a) is estimated as the steepness of an item’s mean score; importantly, both parameters are examined on a latent scale. Finally, while classical test theory calculates the position of an item on the latent trait continuum by comparing test scores with scores of a reference group, in IRT the position is estimated by comparing the distance between items on the ability scale (see Embretson, 1996 for a complete review).

IRT also differs from factor analysis approaches in that the goal of factor analysis is to estimate whether variance shared among scored tasks is better represented by a latent construct that represents a given ability. However, it does not provide information regarding item-level data as IRT models do. In other words, IRT models evaluate how well individuals perform, how well assessments work, and how well individual items in assessments work in the same framework. For these reasons, IRT allows for a specific investigation at the item and individual level, which provides detailed examination of different aspect of test items across a range of items which can provide information about complex span tasks that has been underexplored in the past.

As mentioned, in most IRT analyses, two types of item parameters are commonly modeled and examined: item difficulty (𝛽) and item discrimination (𝛼). Item difficulty is equal to an estimated ability level (𝜃) in which the probability of getting that item correct is the same as getting it incorrect. In other words, a subject with an average ability level is estimated to have a 50% chance of responding correctly to an item of difficulty 0. Item discrimination describes how accurately a given item can differentiate individuals based on ability level. For this purpose, the slope of the item characteristic curve is used to assess whether a specific item mean score has either a steeper curve (i.e., high value) or whether the item has a wider curve (i.e., low value) and, therefore, cannot adequately differentiate based on ability level.

In terms of WMC research, Draheim et al. (2018) used IRT to analyze the difficulty and discrimination parameters of three complex span tasks (i.e., rotation span, operation span, and symmetry span). They found that, generally, items in later blocks presented lower difficulty estimates in two of the complex span tasks, while items in earlier blocks showed higher difficulty estimates, indicating that overall subjects responded more accurately to later blocks than earlier blocks. The authors theorized that subjects might have used a strategy to respond to some of these items, thus impacting complex span scores differently based on the item exposure. This suggests that some complex span tasks may be more prone to task-specific strategies.

The current study builds upon these findings by exploring response differences to item-level data of two spatial complex span tasks and two verbal complex span tasks extracted from different samples. The goal of the study is to understand whether there are relevant differences at the item level in verbal compared to visuospatial complex span tasks. Specifically, whether item-level data supports findings from factor analysis showing that complex span tasks form a uniform domain-general WM construct. We expected IRT to reveal that longer items are more difficult than shorter items for subjects of average ability (because correctly responding to harder items requires more WMC), and more discriminating of subjects’ ability across tasks, supporting the hypothesis that complex span tasks tap a domain-general construct. Based on previous research (Draheim et al., 2018), we also expected to find some differences in difficulty based on block presentation (first vs. last). Critically, by studying the item-level characteristics of the tasks, we expected to identify sources of variation among complex span tasks of different domains that have been reported in the literature with the goal of understanding exactly what complex span scores represent for the underlying mechanisms of WM.

Method

This study was not pre-registered. Data and scripts for these analyses can be found at https://osf.io/bhw87/.

Subjects

The first sample (N = 585) was comprised of subjects from the Georgia Institute of Technology in Atlanta, Georgia, who completed the operation span task and the symmetry span task, as well as other measures. These data are publicly available at https://doi.org/10.1037/pas0000444.supp. The second sample (N = 261) was comprised of subjects from Claremont Graduate University and members of the community in Claremont, California who completed the reading span task and the rotation span task. Data from this sample was collected as part of a previous study that was deemed exempted from Institutional Review Board approval at Claremont Graduate University. All subjects indicated having normal or corrected-to-normal vision.

Measures

Complex span tasks

WMC was assessed using four complex span tasks: operation span, symmetry span, reading span, and rotation span. These tasks are designed to tax both the processing and storage components of WM. Each task consists of multiple items and each item has a varying number of alternative processing and storage stimuli where the processing component is always followed by a storage component. In the processing component, subjects make judgements about a stimulus and in the storage component, subjects memorize a stimulus. At the end of each item, subjects must recall the stimuli presented in the storage component. Subjects complete a total of 12 (visuospatial) or 15 (verbal) items in each task distributed across three consecutive blocks. Each block includes one item of each set size and item sizes vary between 2-5 (visuospatial) and 3-7 (verbal) (see Appendix for further details). Responses are scored and correspond to the item score. (p.13)

In this study, a partial-credit load (PCL) scoring procedure was used to assess subjects’ scores (see Conway et al., 2005). As mentioned, PCL is the sum of correctly recalled storage stimuli from all items, regardless of whether they are perfectly recalled or not. Item scores are weighted based on item size (longer items contribute more to the total score than shorter ones), and partially correct items are scored based on the proportion of correctly responded stimuli in each item. Items scores range from 0 to the number of stimuli presented on a given item. All tasks were automated using E-prime software. Stimuli were presented on a computer screen and responses were collected through mouse click.

Operation span

For each item in the task, the processing component consisted of a mathematical equation (e.g., “(2x2) +1=5”) that was followed by the storage component, a letter. For each set of processing and storage stimuli, subjects had to judge whether the mathematical equation was correct and then memorize the letter. A total of 15 items were presented across three blocks, and item sizes varied from 3 to 7 sets of stimuli. Each item size was randomly presented once in each of the three blocks. The subject’s partial credit score for this task ranges from 0 to 75.

Symmetry span

For each item, the processing component consisted of a figure that was followed by the storage component, a random colored cell in a 4x4 grid. Subjects had to judge whether the figure was symmetrical and then memorize the position of the colored cell in the 4x4 grid. There were 12 items presented across three blocks, with item sizes varying from 2 to 5 sets of stimuli. Each item size was also randomly presented once in each of the three blocks. The subject’s partial credit score for this task ranges from 0 to 42.

Reading span

For each item, the processing component was a sentence followed by the storage component, a random letter. For each set stimuli, subjects had to judge whether the sentences were sensical and then memorize the letters. Item sizes varied from 3 to 7 displays. In total, there were 15 items with stimulus sizes ranging from 3 to 7 presented across three blocks. Each item size was randomly presented once in each of the three blocks. The subject’s partial credit score for this task ranges from 0 to 75.

Rotation span

In this task, the processing component consisted of a rotated letter that was followed by the storage component, a unidirectional arrow. The arrows had eight possible directions and two possible sizes. For each stimuli set, subjects had to judge whether the rotated letter was presented normally (e.g., R) as opposed to horizontally flipped (e.g., Я), and then memorize the direction and size of the arrows. Item sizes varied from 2 to 5 displays for a total of 12 items presented across three blocks and each item size was randomly presented at least once in each block. The subject’s partial credit score for this task ranges from 0 to 42.

Analyses

Although multidimensional approaches to IRT are available, in the current paper we retained the assumption of unidimensionality for all estimated IRT models, and therefore it was assumed that each of the span tasks measured a common trait. To examine differences in the discrimination (𝛼) and difficulty (𝛽) parameters across items sizes and across blocks for each of the four tasks, five models were conducted in this study for each of the four complex span tasks (a total of 20 models): a) Baseline Model: a model in which both types of parameters were constrained across both item size and blocks; b) Model 1: a model with free difficulty parameters across item size; c) Model 2: a model with free discrimination parameters across item size; d) Model 3: a model with free difficulty parameters across blocks; and e) Model 4: a model with free discrimination parameters across blocks.

The purpose of the five models was to compare the baseline model to the models with free parameters to examine whether there was a significant difference between the free models and the baseline models. This approach allowed us to answer four questions for each complex span task:

  1. (1)

    Does item difficulty change as a function of item size? A change in item difficulty as a function of item size would indicate that the difficulty of the items is due to how long that item is, providing information regarding whether short items are too easy or long items are too difficult.

  2. (2)

    Does item discrimination change as a function of item size? A change in item discrimination as a function of item size would indicate that the ability to differentiate among subjects’ ability varies based on the size of the item. This could indicate whether or not short items are adequate indicators of subjects’ ability.

  3. (3)

    Does item difficulty change as a function of block? A change in item difficulty as a function of block would indicate that the difficulty of the items is due to the time point wherein the subjects are presented the stimuli (i.e., in earlier vs. later blocks), indicating whether earlier blocks elicit more accurate responses compared to later blocks.

  4. (4)

    Does item discrimination change as a function of block? A change in item discrimination as a function of block would indicate that the ability to differentiate among subjects’ ability varies based on the time point wherein the subjects are presented the stimuli (i.e., in earlier vs. later blocks). This could provide information regarding whether later blocks are more adequate indicators of subjects’ ability.

As mentioned, partial credit load (PCL) scoring was used for all the tasks, therefore items were allowed to take on a range of scores, not just 0 and 1. We also assumed that items with a small item size would have a lower item discrimination parameter than items with larger item size. Therefore, generalized partial credit models (GPCM; Muraki, 1992) were used to estimate the IRT analyses in the current study. As a polytomous model, GPCM estimates one item threshold parameter for each response category in an item, and also assumes varying item discrimination across items instead of assuming a unitary reliability (reflected as a constant discrimination parameter of 1 across all items). The item threshold parameter is defined as the trait level in which one has an equal probability of choosing the kth response category over the k-1th category in an item. In other words, when choosing between the kth and the k-1 category, subjects with trait levels higher than that threshold are more likely to approach the kth, while subjects with trait levels lower than that threshold are more likely to approach the k-1th. Therefore, for an item of size p (with p+1 response categories, from 0 to p), GPCM estimates p item threshold parameters (from d0 for item scores 0 and 1 to dp-1 for item scores p-1 and p) and 1 item discrimination parameter. All GPCM models in the current study applied the onefold item parameterization (see Chalmers, 2012) and therefore, the overall difficulty parameter (also known as item location parameter; Muraki, 1992) for each item was calculated manually. Following Muraki (1992), the item location parameter was defined as the average of all item threshold parameters for a specific item (e.g., for an item with item size p, its item location parameter β =\(\frac{\sum_0^p{d}_i}{p+1}\) ).

In general, holding all other item characteristics constant (e.g., item size, item discrimination α), higher item difficulty for an item in block A compared to block B means that subjects need to have higher trait ability to respond correctly to the same item in block A than in block B. Individual item sizes in different blocks were considered independent items to examine the differences in item difficulty estimates for each item size in each task. Ability level was specified as N(0,1), indicating that a subject’s ability level followed a normal distribution with a mean of 0 and SD of 1. All item response analyses were conducted using the MIRT package (Chalmers, 2012) in R (Team, 2020). Estimation was conducted using maximum likelihood.

Results

Descriptive statistics

Descriptive statistics and correlations are summarized in Table 1. Operation span and symmetry span data were collected from one sample and reading span and rotation span data were collected from a different sample (see Method). Pearson correlations for all tasks in both samples are also reported. As shown in Table 1, all data were univariate normal and the correlations between tasks for each sample were moderate. However, the correlations for the complex spans for Sample 2 were lower than that of the complex spans for Sample 1.

Table 1 Descriptive statistics by samples and tasks
Full size table

In the current analysis, all IRT models assumed scale unidimensionality (i.e., items within a given task must measure a single trait). To test for the assumption, we conducted four series (one for each task) of exploratory factor analyses and parallel analyses on the item-level data using weighted least square estimation and oblimin rotation. The results from scree plots, parallel analyses, and EFAs with different numbers of factors indicated that a one-factor solution was sufficiently adequate for all four tasks and therefore the assumption was metFootnote 2.

Model fitting

To examine differences in the discrimination (𝛼) and difficulty (β) parameters across items sizes and across blocks for each of the four tasks, five models were estimated. For each of the four complex span tasks, the best model among the five levels of constraints was selected. To choose the best model for each task, we observed model comparison results from log likelihood ratio tests, along with evidence from AIC and BIC parameters. The models were compared in a nested manner such that each model was compared to their alternative with the previous level of constraints (e.g., Model 1 to Baseline, Model 2 to Model 1, etc.). Thus, any significant difference in the likelihood ratio test indicates the rejection of the current level of constraints and therefore retention of the previous model. The model with the best fit should also have the lowest AIC and BIC parameters among all alternatives. Two model fit indices (CFI and RMSEA) are also reported based on the M2* statistic (Cai & Hansen, 2013; Chalmers, 2012). Currently, there are no specific “best practices” for these fit indices, but existing literature indicates that a potentially stricter set of cutoff values may be warranted (e.g., Maydeu-Olivares & Joes, 2006; Cai, Chung, & Lee, 2021). Given the exploratory nature of the analysis, we did not specify arbitrary cut-offs for these two fit indices. For the selected model, item fits were investigated by generalized S-X2 item-fit index with a cut-off of p = .05 (Kang & Chen, 2008; Orlando & Thissen, 2003). Results of item parameters (item discrimination α, item thresholds bi at display-level, and overall item difficulty/location β) have been summarized for the selected model of each task. In addition, item characteristic curves for each selected model are presented in Figs. 2–5.

Fig. 2
figure 2

Item characteristic curves for all tasks items in the retained model (left) and example of item characteristic curve (i.e., Block 2, set size 5 and 7, respectively) (right)

Full size image

As a reminder, the difficulty (i.e., location) estimates (βs) presented in the results are calculated by averaging the display-level threshold parameters for each item and are all on a scale with mean 0. Therefore, a difficulty estimate of β = 1 indicates that, in general, for an item with item size p, a given subject with ability level of 1 standard deviation above the mean has an expected score of 0.5p for that item. Similarly, a β = –1 estimate indicates that, in general, for an item with item size p, a given subject with ability level of 1 standard deviation below the average has an expected score of 0.5p for that item. Thus, items that have difficulty estimates close to 0 (around the mean) are conceptually considered to be items with average difficulty, as a person with average ability would obtain 50% of the total scores on those items, while items that have estimates above or below 0 can be considered “hard” or “easy”, respectively.

Symmetry span (N = 585)

For symmetry span, the best fitting model was Model 2: discrimination (𝛼) constrained by block and freed by item size, and difficulty (β) constrained by block and freed by item size. CFI and RMSEA parameters in all four models were within acceptable range, except for the baseline model. Model fits were not significantly improved by freeing difficulty parameters by block and, thus, the more parsimonious Model 2 was retained. This indicates that for symmetry span, 𝛼 and β are different across items with different sizes but not across items with same sizes but different blocks (see Table 2a). In other words, items become more difficult and more discriminant as item size increases. In addition, items are appropriately difficult at size 5 (see Table 2b).

Table 2 Model statistics for complex span tasks
Full size table

Operation span (N = 585)

For operation span, the best fitting model was Model 3: discrimination (𝛼) constrained by block and free by item size and difficulty (β) freed by block and freed by item size. This indicates that for operation span, 𝛼 and β are different across items with different sizes. Interestingly, β are also different across blocks (for the same size), while 𝛼 parameters are not significantly different for items with the same size across blocks (see Table 3a). In other words, as it is expected, items become more difficult and more discriminant as item size increases. However, items of a given size are also more difficult in block 1 compared to block 3 (see Table 3c). In addition, in all models except for the baseline model, RMSEA indices were within acceptable range, but not CFI indices, especially for Models 1 and 2. Overall, the model fit indices of the selected model were within acceptable range.

Table 3 Model fitting parameter for best (chosen) model both constrained and freed by block across all complex span tasks
Full size table

Rotation span (N = 261)

For rotation span, the best fitting model was Model 2: discrimination (𝛼) constrained by block and freed by item size and difficulty (β) constrained by block and freed by item size. This indicates that just like for symmetry span, for rotation span, 𝛼 and β are different across items with different sizes but not across items with same sizes but different blocks (see Table 4a). Specifically, items become more difficult and more discriminant as item size increases. However, just like it was the case for symmetry span, items in rotation span become appropriately difficult at size 5 (see Table 4b). CFI and RMSEA parameters in all four models were within acceptable range, except for the baseline model.

Table 4 Additional analyses. Four-way ANOVAs
Full size table

Reading span (N = 261)

For reading span, the best fitting model was Model 2: discrimination (𝛼) constrained by block and free by item size and difficulty (β) constrained by block and free by item size. This indicates that in reading span, 𝛼 and β are different across items with different sizes but not across items with same sizes but different blocks (see Table 5a). This indicates that, unlike in operation span, there was not a significant difference in items across blocks. However, by examining the item parameters, it can be observed that there is a nonsignificant decreasing trend by block for difficulty estimates. While this change is not significant in this study, it suggests that reading span could follow the same pattern as operation span (Table 5c) to a lesser extent. Overall, in reading span, items get more difficult as item size increases, nevertheless, all items seem to be generally too easy (see Table 5b). CFI and RMSEA parameters in all four models were within acceptable range, except for the baseline model. In addition, the selected model presented improved CFI compared to Model 1, supporting model comparison.

Summary of results

Overall, the results present convergent patterns in psychometric properties across all four tasks. That is, item discrimination and difficulty parameters in all four tasks changed as a function of item size. Specifically, as expected, all four tasks presented a trend of increasing difficulty by item size, such that longer items were more difficult than shorter items. In addition, the results show that regardless of the sample or the task, most task items were psychometrically “easy”, with a majority of difficulty parameters being negative. This suggests that most subjects of below average ability would still be able to respond correctly to most items in the tasks, as it was also suggested by Draheim et al. (2018) and Oswald et al. (2015).Footnote 3

The results of these tasks were also divergent in certain aspects. First, the verbal complex span tasks presented a trend of decreasing difficulty across blocks that was significantly different for operation span. That is, subjects showed a tendency to answer on average more accurately to items of the same size in block 3 than block 1. Second, the visuospatial span tasks did not present such a pattern of decreasing difficulty. In fact, items in the visuospatial tasks were largely stable across blocks regardless of the stimuli. Third, in general, all four tasks were relatively easy according to the difficulty parameters, suggesting that on average subjects with below-average ability could answer most items correctly. In addition, the patterns of the difficulty parameters in the verbal compared to visuo-spatial tasks were different. While the verbal tasks were overall too “easy”, that is, they had overall low difficulty estimates even in the longer item sizes, the visuospatial tasks presented very low difficulty estimates in shorter item sizes and higher estimates in only the longest item size (i.e., 5). These findings are discussed further below.

It is worth noting that some item response categories did not present an ordered decline; for example, in symmetry span, block 1 of set size 2 and block 1 of set size 3 (– 1.20 vs. – 1.35) or in reading span, block 2 of set size 7 and block 3 of set size 7 (– .74 vs. – 1.02). These instances could indicate that for these tasks, a dichotomous model of IRT might also be a valid approach to examining responses to complex span tasks at the item level. However, in this study, task scores were calculated using the partial-credit load method widely used to score complex span tasks (PCL; Conway et al. 2005), which considers that tasks responses are polytomous by design and that the range of response categories are necessary to appreciate subtle individual differences in task response. For this reason, a generalized partial credit IRT model (GPCM) was used to examine the polytomous responses to complex span tasks in this study. The lack of ordered responses in some of the tasks’ blocks suggests that some of these responses might be redundant, nevertheless, given the theoretical framework in which the tasks are considered, we estimated that a polytomous IRT approach was the most adequate solution in this case.

Additional results

Based on the results obtained through the IRT approach, one of the key insights was that difficulty in the verbal complex span tasks presented a decreasing trend in later blocks compared to earlier blocks, however this was only a significant effect for the operation span task. To further investigate this result, we decided to conduct traditional analyses to examine the possible nature of this trend. To this end, we conducted four four-way ANOVAs comparing each of the four blocks in each task. The results are presented in Table 4. The results of the ANOVAs indicated that both verbal tasks showed practice effects as evidenced by significant differences in performance among Blocks 1 and 2 and Blocks 1 and 3 (operation span) and Blocks 1 and 3 and Blocks 2 and 3 (reading span), such that scores in latter blocks were significantly higher than scores in former blocks (see Table 4). This was not the case for symmetry and rotation span tasks. Overall, these additional analyses provide support for the view that the decreasing difficulty trends found for verbal complex span tasks using IRT are likely the result of practice effects.

Discussion

The goal of this study was to explore whether there are relevant differences in responses at the item level in verbal compared to visuospatial complex span tasks to understand if findings at the item level support research showing that variance in complex span tasks represents a domain-general WM ability.

The current findings suggest that examining complex span responses through IRT can explain specific aspects of complex span tasks that have not been examined before. Specifically, the results of the study showed that there were discrepancies in the item-level responses across the complex span tasks examined in this study. First, all tasks reflected relatively low difficulty when it comes to the difficulty parameter estimates. However, this finding was not homogenous across the domain-specificity of the tasks. Specifically, verbal tasks seemed to be overall easier compared to spatial tasks (even for longer items), presenting lower difficulty estimates than the longer items of the spatial tasks. For example, an item of set size 7 (b = – .60) for operation span is about as difficult as an item of set size 5 (b = – .63) for rotation span. This suggests that the stimuli displayed in the verbal tasks might elicit different response processes compared to the stimuli displayed in the spatial tasks, though this necessitates further investigation.

Regarding the visuospatial tasks, they also presented low difficulty estimates, however this was true for all item sizes except for the longest item size (i.e., item size 5). In addition, middle-size items in the visuospatial tasks (i.e., those items in the middle of the set) did not seem to provide much information about ability differentiation based on the difficulty estimates. In other words, items in the middle of a set did not differentiate across subjects accurately.

Finally, in terms of difficulty, there was a trend for items presented in a later block of the verbal tasks to have lower difficulty scores than those in earlier blocks, especially for the operation span task. That is, although difficulty seemed to generally increase as a function of item size (i.e., longer items were more difficult than shorter items) across all tasks, difficulty tended to decrease by block (i.e., items in later blocks were less difficult than items in earlier blocks) in the verbal tasks. This suggests that, despite inducing proactive interference, at the item-level, subjects may be responding more accurately to items of a certain size after those items have been presented more times (compared to fewer times) in verbal tasks, perhaps suggesting practice effects. Alternatively, this pattern could also suggest that even though proactive interference is operating in complex span tasks, verbal tasks might be more prone to the use of verbal strategic processes, and these processes might become more sophisticated across the duration of the tasks, perhaps due to rehearsal strategies.

One implication of these findings is that verbal tasks might elicit different types of responses at the item-level compared to spatial tasks, perhaps indicating that verbal complex span tasks can facilitate the use of strategies that can in turn help complete the tasks more efficiently. Recalling letters (i.e., reading span), for example, might be more prone to strategy use or to relying on previous knowledge than recalling the direction of arrows (i.e., rotation span), as it has been previously suggested (Turley-Ames & Whitfield, 2003). Similarly, completing multiple blocks of this task might facilitate practice of the stimuli, thus reducing the need to engage domain-general working memory. This would indicate that despite their contribution to general WM (Kane et al., 2004), responses to verbal tasks might be more prone to reliance on mechanisms other than domain-general processes compared to visuospatial tasks.

Another issue to consider is why the reading span task only showed a nonsignificant trend compared to operation span in the IRT analyses. It is possible that there are inherent differences between reading and operation span items that are largely based on the quality of their stimuli, such as the type of processing component used. Similarly, there might be factors regarding the characteristics of the samples tested that could explain this difference. In fact, while this effect was not significant using the IRT approach, a significant difference was found using classical test theory analyses. Specifically, the results of ANOVAs showed that performance in latter blocks was significantly higher than performance in former blocks for both verbal tasks, but not for the visuospatial tasks. In addition, it should be noted that the reading and operation span data used for the IRT analyses come from different samples. While both sample sizes are appropriate for the analyses, the sizes differ from each other, which could potentially increase the variability in task responses differently. Further, the reading span data comes from a sample of mostly graduate students of Claremont Graduate University and members of the community of the highly diverse Southern California area of the San Gabriel Valley. Because of this, the reading span data come from a generally older and diverse population in terms education, SES, and race. On the other hand, the operation span data come from a sample of largely undergraduate students from the highly selective Georgia Institute of Technology. The difference in the composition of the samples could partly influence the nonsignificant trend observed in reading span in the IRT analyses; in fact, the correlation between the tasks in each sample was lower for the rotation and reading tasks (.37) than for the operation and symmetry tasks (.54). Further, the reading span sample presented a significantly higher complex span score than the operation span sample (t (665.50) = – 2.47, p = .014), but there was no difference between samples in terms of visuospatial tasks scores (t (591.32) = – 1.37, p = .170).Footnote 4

A wider implication of these findings is the extent to which they can provide information for psychometric research and application. Regarding psychometrics, the executive attention theory of WM posits that domain-general attentional resources drive individual differences in WM (Engle et al., 1992; Engle et al., 1990; Kane & Engle, 2000). Thus, higher levels of attentional control are predictive of higher levels of WM and vice versa. In line with this, complex span tasks are thought to capture attentional control abilities in addition to domain-specific abilities. According to executive attention theorists, the predictive validity of complex span tasks is driven mainly (if not solely) by the domain-general attentional component of WM. However, the current findings suggest that performance on complex span tasks, especially verbal, might reflect a higher involvement of domain-specific general processes than previously thought. This is consistent with findings by Draheim et al. (2018) and Mackintosh and Benett (2003), among others.

Not only do these findings challenge executive attention theory, but they also speak to other theories of working memory that have a domain-general emphasis. For example, Oberauer’s theory of working memory (which is an extension of Cowan’s embedded process model of WM) posits that working memory is an ability composed of active long-term memory, a direct-access region, and a focus of attention (Oberauer, 2009). The focus of attention serves as the domain-general region of working memory that is bottlenecked by binding processes and response-selection processes. The findings reported here would suggest that considering domain-specific processes to a greater degree would be important in Oberauer and Cowan’s theory of working memory (Cowan, 1988; Cowan, 2001; Cowan, 2017) as well.

These findings could indicate that examining purely domain-general WM without considering domain-specificity might not be possible when using complex span tasks. This has implications for research that administers complex span tasks to measure WMC as a secondary measure. For example, studies that concern linguistic outcomes or bilingual subjects might not want to use the operation span as a single measure of WMC. Similarly, research that examines mental rotation performance should not solely use the rotation span. One reason why we found differences at the item-level for each domain might be related to the sample tested in this study. If the WMC of the sample is highly similar, it is more likely to find differences in the domain-specific component of the tasks. This is because the lower the probability of failing the processing component of the tasks that requires domain-general processes, the more likely it is that individual differences in specific processes will matter to obtain a correct response in the tests. Theoretical accounts (Kovacs & Conway, 2016) have proposed that this could be the cause of the phenomenon of factor differentiation also known as the Law of Diminishing Returns (Spearman, 1927). Since the samples tested in this study were part of a selected group of students from higher education institutions and were more likely to resemble each other in terms of domain-general WM than in individual differences in specific processes, this could be part of the reason behind our results. Further, we have discussed that complex span tasks have been largely shown to load onto a domain-general WM factor, and this WM factor is usually more highly related to fluid reasoning than simple tasks. This relationship is thought to be due to the extent to which general processes (e.g., executive functioning, attention) are tapped by complex span tasks (Kovacs & Conway, 2016), suggesting that all complex span tasks tap central executive processes involved in WM, regardless of domain. However, as mentioned above, a WM factor based on verbal complex tasks is not as strong a predictor of fluid reasoning as a factor extracted from spatial complex span tasks (Kane et al., 2004). Consequently, as opposed to previously thought, differences in specific processes could indicate that the relevance of a specific process for task performance might vary based on the overlap of multiple factors, such as previous knowledge or practice, instead of assuming that all specific domains require the same type/amount of processes to be engaged. This idea should be further explored.

Finally, the current findings provide implications for selection among current measures of WM. Based on these findings, two suggestions could be made regarding the use of complex span tasks. First, if only one task is employed to measure WMC, it is advisable to give preference to visuospatial span tasks compared to verbal tasks. This is especially relevant given that a large number of studies have used only the operation span as a measure of general WM (Foster et al., 2015). Our findings and others’ (i.e., Draheim et al., 2018) show that a WM span score based solely on responses to verbal tasks, and especially, the operation span, could be inflating subjects’ true scores. This should be carefully considered by researchers whose samples include individuals with higher-than-average WMC. Second, our results showed that items that are not too short or not too long (e.g., 3) are generally not sufficiently difficult, providing less information about subjects’ ability. This suggests that it might be advisable to replace these items for a larger number of short and long items (for example, by presenting more blocks of each). This is consistent with solutions proposed by researchers that observed domain-specific differences in responses to complex span tasks. For example, Draheim et al. (2018) and Oswald et al. (2015) have proposed modifications to complex span tasks, such as eliminating smaller set sizes or incorporating longer set sizes. Given that researchers tend to use only one complex span task to assess WM, another solution could be to include more blocks of shorter and longer set sizes when using visuospatial tasks. This could help increase ability differentiation by detecting responses that are the result of lack of motivation or fatigue (i.e., incorrect responses to the shorter set sizes) and reducing time spent on middle-size items that do not provide significant information about the subjects’ ability. Our results suggest that this approach might help better capture general ability when using visuospatial tasks while maximizing time resources and minimizing fatigue. Instead, for verbal tasks, shorter items provide poorer discrimination, especially in later blocks. This could be remedied by reducing the number of blocks or reducing the number of short-sized items in verbal tasks. This is an important consideration for both research and practice.

One limitation of this study is the inability to examine item-level responses to the processing component of the complex span tasks, such as the arithmetic problems of the operation span and the multidirectional arrows of the rotation span. The nature of these stimuli might differ in difficulty; indicating the syntactic validity of a sentence might be more prone to strategies or relying on previous knowledge than remembering the positions and size of arrows in space. This could perhaps contribute to the subjects’ overall WM span scores. While these data were not available for the current samples, future research examining the impact of the domain-specificity of processing stimuli using IRT would be valuable for the improvement of complex span tasks. In addition, it should be noted that this study was conducted among two highly selective samples; both groups were undergraduate and graduate students of higher education institutions in the US, and both were formed largely by young adults. Therefore, it is possible that the results reported in this study only apply to average-to-high performing samples. As suggested above, a high homogeneous WMC in the samples could partly explain why we observed stronger differences in domain specificity. This could indicate that for high performing samples, WMC assessed by complex span tasks might benefit from the use of visuospatial tasks with fewer short items to discriminate individual abilities adequately. However, Draheim et al. (2018, Experiment 2) recruited subjects from one of the same subject pools, the Georgia Institute of Technology, which included average as well as above-average individuals and found that modified complex span tasks designed to discriminate above-average ability individuals were more discriminating for participants in the higher end of the working memory capacity range (i.e., especially those about .5 SDs above the mean), indicating that regular complex span tasks are not necessarily unchallenging for average and high performing individuals. Still, it is likely that the samples in this study include average to above-average subjects and fewer below-average subjects. In other samples, including clinical samples or older adults, the results and the proposed solutions might not be applicable and further research should examine whether different types of complex span tasks tend to elicit different responses at the item level in different populations, as well as what remedies should be considered.

In conclusion, the current study found that, while complex span tasks are strong measures of domain-general WM, there seem to exist differences at the item-level in terms of domain-specificity that have been understudied before. Our findings indicate that verbal complex tasks tend to be less difficult for most average-ability subjects to complete successfully, and they could be more prone to practice effects and strategy building compared to visuospatial tasks. Overall, the results of our study suggest that the role of domain-specific processes in complex span tasks should be examined more carefully and task selection should be based on the research area and variables of interest to avoid inflated WMC scores.