Abstract
An optical unitary processor (OUP) is a programmable photonic circuit to achieve arbitrary unitary operation for various applications, including optical communication, deep learning, and quantum computing. Conventionally, OUPs are implemented by cascading 2 × 2 reconfigurable interferometers, but this scheme cannot easily be extended to multiple wavelength and polarization channels due to the strict requirement to employ 50:50 beam splitters. Here, we demonstrate that an OUP using multiport directional couplers (DCs) can realize independent unitary conversion of multiple wavelength and polarization channels simultaneously. This OUP is based on the multi-plane light conversion (MPLC) principle, which does not require a specific transformation at each layer, unlike the conventional scheme. Thanks to this unique robustness of the MPLC method and strong wavelength/polarization dependence of multiport DCs, we numerically show that independent unitary transformations can be applied to up to 16 channels (2 polarization × 4 wavelengths) using a single device.
Export citation and abstract BibTeX RIS
1. Introduction
An integrated optical unitary processor (OUP) can convert mutually orthogonal spatial modes into arbitrary spatial modes on a compact photonic chip. It is widely researched for optical communication, 1–3) deep learning, 4–13) and quantum information processing, 14–21) and so on. For example, space-division multiplexing is the key technology to enable high-capacity optical transmission systems, but the mode coupling inside the few-mode fiber is inevitable due to the physical perturbations such as bending and twisting of the fiber. In this case, an OUP can be employed as an all-optical multi-input multi-output (MIMO) demultiplexer to compensate for the mode coupling effect. 22) Compared with the conventional MIMO process by digital signal processing, all-optical MIMO offers unique advantages such as bit-error-independent low-power operation.
Besides optical communication, integrated OUPs may also be used in realizing potentially low-power and high-speed artificial neural networks (ANNs). An ANN generally consists of multiple hidden layers connecting the artificial neurons, which rely heavily on linear matrix multiplications. Since any linear matrix can be decomposed into unitary matrices and a diagonal matrix through the singular-value decomposition, this process can be implemented by using OUPs. As a result, linear transformation can be performed at the speed of light with minimal power consumption, which makes this approach substantially energy-efficient and faster than its electronic counterparts. 4)
An integrated N × N OUP is mainly implemented by the cascaded Mach–Zehnder interferometers (MZIs), which consist of two 2 × 2 beam splitters and phase shifters. 23–25) While there have been several experimental demonstrations, the MZI-based OUP requires perfect 50:50 beam splitters to achieve arbitrary unitary operation. 23–26) As a result, the directional couplers (DCs) or multimode interference (MMI) couplers, which are commonly used as beam splitters, need to be designed precisely for the specific polarization and wavelength of interest. Thus, the MZI-based OUP cannot be directly extended to wavelength- and polarization-division-multiplexed signals.
In this paper, we demonstrate that an OUP using multiport DCs can realize independent unitary conversion for multiple wavelength and polarization channels simultaneously. This OUP is based on the multi-plane light conversion (MPLC) principle, 27,28) which does not require a specific transformation at each layer, unlike the MZI-based OUP. 3,29–39) The MPLC-based OUP consists of cascaded stages of dense unitary mixing layers and arrayed phase shifter layers. A multiport DC, which is used as the mixing layer, exhibits different unitary transformations depending on the wavelength and polarization state. Therefore, with a sufficient number of stages, the MPLC-based OUP using multiport DC can realize independent and arbitrary spatial unitary conversions of multiple wavelength and polarization channels. This paper is an extended version of short conference proceedings 40) including further information and analysis about the requirement of phase shifter stages.
2. Device schematic
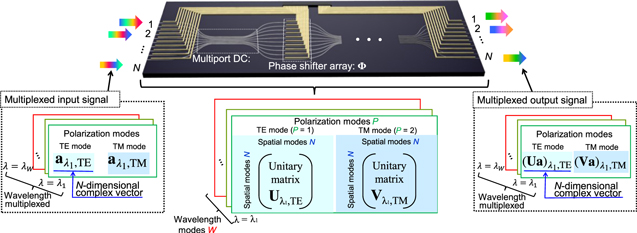
Figure 1 shows the schematic of the MPLC-OUP using multiport DCs. It consists of the cascaded mode mixers and phase shifter arrays. The transfer matrix of OUP can be written as
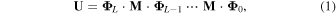
where M and Φ are the transfer matrices of each mode mixer and a phase shifter array, and L is the number of cascaded stages. By adjusting the phase shifters properly, the OUP realizes arbitrary unitary transformation.28)
Fig. 1. (Color online) Schematic of MPLC-OUP using multiport directional couplers. When the wavelength- and polarization-multiplexed N-dimensional complex vectors are input, the OUP can apply independent and arbitrary unitary transformations to all wavelength and polarization channels simultaneously.
Download figure:
Standard image High-resolution imageConsidering the freedom of the unitary matrix, the number of stages L should satisfy
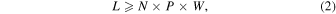
where P and W are the numbers of polarization and wavelength channels, respectively. The total number of phase shifters is N × L. Similar to the previous works, 26,28) we adjust the phase shifters to examine whether it is possible to simultaneously achieve desired unitary transformations for all P × W independent channels.
While an MPLC-based OUP does not require specific transformation at each layer, it does require M in Eq. (1) to be a dense N × N unitary matrix. 26,41) One important advantage of using an N-port DC to implement M is that it is inherently lossless and provides sufficient coupling among all the ports, 31,39) so that M is a dense unitary matrix, regardless of the wavelength and polarization. At the same time, it generally has a strong wavelength and polarization dependence, so that different unitary transformations can be applied to different polarization/wavelength channels. With a sufficiently large L, therefore, we can expect that arbitrary unitary conversion should be achieved for each polarization/wavelength channel using a single device.
3. Results and discussion
Numerical simulation is carried out to investigate the feasibility of simultaneous unitary conversions for multiple wavelength and polarization channels. We compare three cases with (P, W) = (1, 1), (1, 3), and (2, 3) for N = 4 and 8, respectively. When W = 3, we set the three wavelengths to be 1540 nm, 1550 nm, and 1560 nm. A standard silicon-photonic circuit with 440 nm waveguide width and 220 nm thick silicon-on-insulator device layer is assumed. The multiport DC is designed to have the gap and the coupler length of 250 nm and 40 μm, respectively. The transfer matrix of multiport DC is calculated by the eigenmode expansion method at each wavelength for the transverse-electric (TE) and transverse-magnetic (TM) polarization modes. We assume ideal lossless phase shifters, each driven independently by an 8-bit digital-to-analog converter. While we ignore the wavelength/polarization dependence of the phase shifter for simplicity, its effect will be discussed in Sect. 4.
In each case, we generate 24 sets of Haar random N × N unitary matrices { } as the target transformations for all P × W wavelength/polarization channels. Then, we calculate {
} as the target transformations for all P × W wavelength/polarization channels. Then, we calculate { }, which are the actual transfer matrices realized by the OUP. The deviation between
}, which are the actual transfer matrices realized by the OUP. The deviation between  and
and  is evaluated by the mean-square-error (MSE), which is defined as
is evaluated by the mean-square-error (MSE), which is defined as
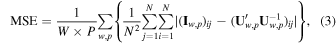
where I is an N × N identity matrix. We employ the simulated annealing algorithm in tuning all phase shifters to minimize the MSE.
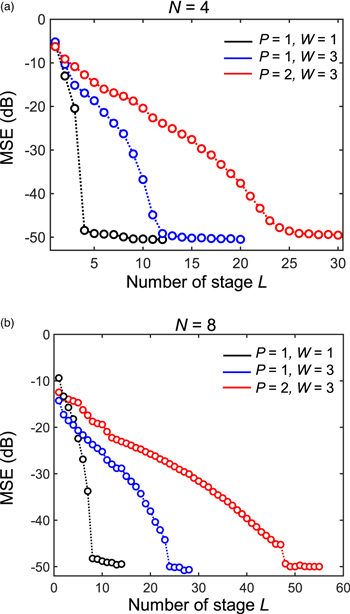
Figures 2(a) and 2(b) show the MSE as a function of the numbers of stages L after training all phase shifters for N = 4 and 8, respectively. In all cases, the MSE is suppressed below −45 dB when L ≥ NPW. Owing to the strong wavelength/polarization sensitivity of the N-port DCs assumed in this work, similar OUP performance is obtained for all wavelength/polarization channels compared with the single wavelength and polarization case.
Fig. 2. (Color online) Calculated MSE after optimizing the phase shifters as a function of L with (P, W) = (1, 1), (1, 3), and (2, 3) for N = 4 and 8.
Download figure:
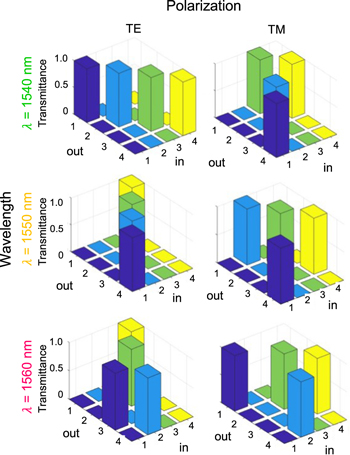
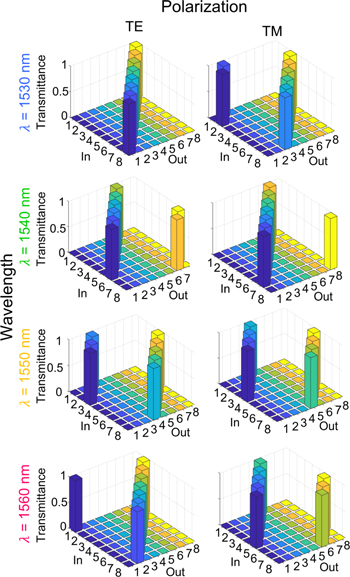
Standard image High-resolution imageTo demonstrate the performance at a larger number of channels, Figs. 3 and 4 show the obtained { } in example cases with (N, P, W) = (4, 2, 3) and (8, 2, 4) for L = 24 and 64, respectively. Here,
} in example cases with (N, P, W) = (4, 2, 3) and (8, 2, 4) for L = 24 and 64, respectively. Here,  is set to be different permutation matrices for respective wavelength/polarization channels. For the case of W = 4, the wavelengths are set to be 1530, 1540, 1550, and 1560 nm. From Figs. 3 and 4, we can see that all 6 (3 wavelengths × 2 polarizations) or 16 (8 wavelengths × 2 polarizations) channels are processed simultaneously to achieve desired 4 × 4 and 8 × 8 unitary operations, which are set independently for each channel, respectively.
is set to be different permutation matrices for respective wavelength/polarization channels. For the case of W = 4, the wavelengths are set to be 1530, 1540, 1550, and 1560 nm. From Figs. 3 and 4, we can see that all 6 (3 wavelengths × 2 polarizations) or 16 (8 wavelengths × 2 polarizations) channels are processed simultaneously to achieve desired 4 × 4 and 8 × 8 unitary operations, which are set independently for each channel, respectively.
Fig. 3. (Color online) Obtained {U'} in an example case of realizing different permutation matrices {U} for six wavelength/polarization channels with L = 24.
Download figure:
Standard image High-resolution imageFig. 4. (Color online) Obtained {U'} in an example case of realizing different permutation matrices {U} for eight wavelength/polarization channels with L = 64.
Download figure:
Standard image High-resolution image4. Effect of channel-dependent phase shifters
In the previous section, we have assumed ideal wavelength/polarization-independent phase shifters. In practice, however, silicon photonic phase shifters generally exhibit wavelength/polarization dependences, which need to be considered. Since a channel-dependent phase shift can be treated as a difference in the mode mixers, it is expected that such dependencies would not have substantial influence on the overall performance. To confirm this assumption, we study the effect of wavelength and polarization dependences of phase shifters on the multi-channel operation, assuming a thermo-optical (TO) silicon-photonic phase shifter as an example case of interest.
We consider a TO phase shifter with a 200 nm thick aluminum heater, which is placed 2 μm above the silicon waveguide covered by a silicon oxide cladding layer. The dimension of the heater is set to be 2 μm × 250 μm. We assume dn/dT = 1.8 × 10−4 for silicon, 42,43) where n and T are the refractive index and temperature, respectively. The heat transport within the cross-sectional structure is calculated by the finite-element method. The optical modes and effective refractive index for each heat distribution is calculated by the finite-difference method.
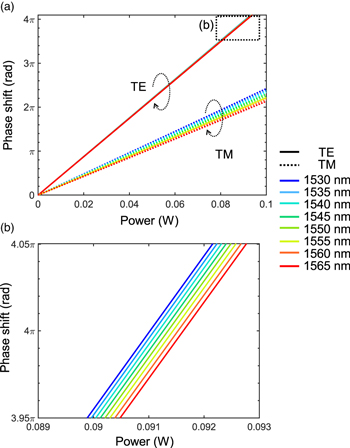
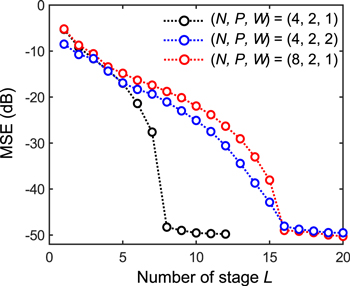
Figure 5 shows the calculated phase shifts for TE and TM modes in various wavelengths as a function of applied power to the heater. The 2 phase shift is achieved at around 46 mW (TE) and 94 mW (TM), respectively, while the wavelength dependence is relatively small. Figure 6 shows the obtained MSE of the OUP performance, which is calculated using the wavelength/polarization dependences in Fig. 5. In all cases of (N, P, W), the MSE is suppressed below −45 dB when L ≥ NPW, similar to the cases shown in Fig. 2. Therefore, even if the phase shifters have polarization/wavelength dependence, the performance of multi-channel OUP is comparable to that of the simplified case with polarization/wavelength-independent phase shifters.
phase shift is achieved at around 46 mW (TE) and 94 mW (TM), respectively, while the wavelength dependence is relatively small. Figure 6 shows the obtained MSE of the OUP performance, which is calculated using the wavelength/polarization dependences in Fig. 5. In all cases of (N, P, W), the MSE is suppressed below −45 dB when L ≥ NPW, similar to the cases shown in Fig. 2. Therefore, even if the phase shifters have polarization/wavelength dependence, the performance of multi-channel OUP is comparable to that of the simplified case with polarization/wavelength-independent phase shifters.
Fig. 5. (Color online) Numerically simulated polarization and wavelength dependence of TO phase shifter. (a) Full-scale plot and (b) enlarged plot at the range shown by the dotted square in (a).
Download figure:
Standard image High-resolution imageFig. 6. (Color online) Calculated MSE after optimizing polarization-dependent TO phase shifter as a function of L with (N, P, W) = (4, 2, 1), (4, 2, 2), and (8, 2, 1).
Download figure:
Standard image High-resolution image5. Conclusions
We have demonstrated that an MPLC-based OUP with multiport DCs can be designed to realize independent unitary transformations for polarization- and wavelength-multiplexed input signals. Due to the inherent flexibility of the MPLC scheme and the strong wavelength/polarization dependence of a silicon-photonic multiport DC, the proposed OUP can be configured to perform independent unitary conversions for multiple wavelength and dual-polarization channels. Moreover, we also discuss the case where the phase shifters have polarization and wavelength dependence and show that the OUP performance is not degraded due to the channel dependence. These results show that the MPLC-based OUP can be extended to wavelength- and polarization-multiplexed channels by simply adding extra number of stages without the need for wavelength/polarization demultiplexers. This should be useful particularly for optical communication applications, where all-optical demultiplexing of spatial/wavelength/polarization modes is desired by a compact device with a minimal footprint.
Acknowledgments
This work is financially supported by the JSPS KAKENHI (Grants Nos. JP20J21861, JP21K18168 and MbSC2030). The authors thank Taichiro Fukui, Go Soma, and Kento Komatsu for the fruitful discussion.