Abstract
The GaN thickness dependence of surface structural stability and adsorption behavior of Ga adatom in GaN layers on a AlN(0001) surface are investigated on the basis of first-principles calculations to clarify the self-limiting growth on AlN(0001) surface during metal-organic vapor phase epitaxy. The calculations demonstrate that the stability of reconstructed GaN layers on a AlN(0001) surface is similar to that of a GaN(0001) surface irrespective of the GaN film thickness. Furthermore, we find that the adsorption of a Ga adatom on the AlN(0001) surface easily occurs compared with that on AlN(0001) surface with GaN layers. The difference in the adsorption behavior implies that the growth of GaN layers on a AlN(0001) surface is suppressed. The calculated results provide theoretical guidance for understanding the self-limiting growth of GaN layers, resulting in the formation mechanism of GaN quantum wells.
Export citation and abstract BibTeX RIS
1. Introduction
Light-emitting diodes (LEDs) and laser diodes (LDs) using nitride semiconductors have been actively studied, and light-emitting devices in various wavelengths have been realized. In addition to InGaN-based semiconductors for light-emitting devices in the visible region, AlGaN-based semiconductors are attracting interest from researchers as a material for light-emitting devices in the deep ultraviolet (DUV) region (200–300 nm).
1–10) In general, AlGaN/AlN quantum well (QW) structure is fabricated in which a AlN layer with a large band gap energy sandwiches a AlGaN layer with a small band gap energy to increase the luminous efficiency of the AlGaN layer. Alternatively, GaN QW can be used as the emitting layer since high internal quantum efficiency is obtained.
11) For light-emitting devices in the DUV region, ultrathin GaN QWs are required. Indeed, it has been recently reported that the thickness of GaN films on a AlN surface grown by metal-organic vapor phase epitaxy (MOVPE) can be controlled on one and two-bilayer scales on (0001) and  planes, respectively, owing to the balance between crystallization and the evaporation of Ga adatoms at the surface.
12) The formation of GaN/AlN QWs results in higher luminescence efficiencies than conventional Alx
Ga1−x
N QWs. Although the balance is recognized as a consequence of self-limiting growth of GaN on a AlN surface, the atom-scale mechanism of the self-limiting growth of GaN on a AlN surface is still unknown. The understanding of self-limiting growth could be accomplished by clarifying the surface stability and growth kinetics of GaN layers on AlN surfaces.
planes, respectively, owing to the balance between crystallization and the evaporation of Ga adatoms at the surface.
12) The formation of GaN/AlN QWs results in higher luminescence efficiencies than conventional Alx
Ga1−x
N QWs. Although the balance is recognized as a consequence of self-limiting growth of GaN on a AlN surface, the atom-scale mechanism of the self-limiting growth of GaN on a AlN surface is still unknown. The understanding of self-limiting growth could be accomplished by clarifying the surface stability and growth kinetics of GaN layers on AlN surfaces.
In our previous study, we investigated the surface structural stability and adsorption behaviors of AlN and GaN surfaces at various plane orientations by using first-principles calculations, and clarified the relationship between the surface structure and growth condition. 13–19) Furthermore, the behavior of Ga and Al adatom on GaN(0001) and AlN(0001) surfaces, respectively, has been clarified by calculating the adsorption energies. 15, 20–22) However, the adsorption behavior of Ga adatom on a Al(0001) surface and GaN layers on a AlN(0001) surface has never been clarified. In order to clarify the mechanism of self-limiting growth, we investigate the thickness dependence of surface structural stability of GaN layers on a AlN surface on the bases of first-principles calculations. In addition to the structural stability of GaN layers, 23) we examine the adsorption behavior of Ga adatoms on GaN layers on a AlN(0001) surface to clarify the effect of growth kinetics on self-limiting growth.
2. Methodology
In this study, we use the slab models composed of n (n is the number of GaN bilayers) layers of GaN and AlN(0001) surface. The AlN(0001) surface consists of four AlN bilayers. Approximately 25 Å of the vacuum region is included along the [0001] direction. The bottom surface of slabs is passivated by artificial H atoms. 24) We use the calculated lattice parameters of AlN (a = 3.12 Å, c = 5.02 Å), which agree with experiments within the error of 0.8%.
The reconstructions for n = 0 (i.e. AlN(0001) surface) are considered on the basis of the electron counting (EC) rule. 25) Figures 1(a)–1(e) show the reconstructions of the AlN(0001) surface. In addition to the ideal AlN surface (Ideal AlN) shown in Fig. 1(a), the (2 × 2) surface with three H atoms (3Al-H) shown in Fig. 1(b) and the (2 × 2) surface with a Al-H bond and a H-terminated N adatom (Nad-H + Al-H) shown in Fig. 1(c) are considered. Furthermore, the (2 × 2) surface with a H-terminated N adatom and NH2 (Nad-H + Al-NH2) shown in Fig. 1(d) and the (2 × 2) surface with three NH2 and one NH3 (Al-NH3+3Al-NH2) shown in Fig. 1(e) are considered. The reconstructions for n = 1 considered in this study are shown in Figs. 1(f)–1(j). In addition to the ideal GaN surface (Ideal GaN) shown in Fig. 1(f), the (2 × 2) surface with a Ga-H bond and a H-terminated N adatom (Nad-H + Ga-H) shown in Fig. 1(g) and the (2 × 2) surface with a H-terminated N adatom and a NH2 (Nad-H + Ga-NH2) shown in Fig. 1(h) are considered. Moreover, the (2 × 2) surface with a Ga adatom (Ga adatom) shown in Fig. 1(i) and Ga bilayer surface (Ga bilayer) shown in Fig. 1(j) are considered.
Fig. 1. (Color online) Top views of calculation models of AlN(0001) surface and 1ML GaN on AlN(0001) surface considered in this study. The models for (a) the ideal AlN(0001) surface (Ideal AlN), (b) the (2 × 2) surface with three H atoms (3Al-H), (c) the (2 × 2) surface with Al-H bond and H-terminated N adatom (Nad-H + Al-H), (d) the (2 × 2) surface with H-terminated N adatom and NH2 (Nad-H + Al-NH2), (e) the (2 × 2) surface with three NH2 and one NH3 (Al-NH3+3Al-NH2), (f) the ideal surface of 1ML GaN on AlN(0001) surface structure (Ideal GaN), (g) the (2 × 2) surface with Ga-H bond and H-terminated N adatom (Nad-H + Ga-H), (h) the (2 × 2) surface with H-terminated N adatom and NH2 (Nad-H + Ga-NH2), (i) the (2 × 2) surface with Ga adatom (Ga adatom), and (j) Ga bilayer surface (Ga bilayer) are considered. Blue, green, purple, and pink circles denote Al, Ga, N and H atoms, respectively. Graphics visualization was performed using VESTA. 26)
Download figure:
Standard image High-resolution imageFigure 2 shows the schematic side views of calculation models of the n layer of GaN on a AlN(0001) surface. For n = 0, as shown in Fig. 2(a), only AlN(0001) surface is considered. On the other hand, one, two, and three layers of GaN bilayers are stacked on the AlN(0001) surface for n = 1, 2, and 3, respectively, as shown in Figs. 2(b), 2(c), and 2(d). The surface structural stability and adsorption behavior of Ga adatoms are examined by changing the number of GaN layers.
Fig. 2. (Color online) Schematic side views of calculation model of n layer of GaN on AlN(0001) surface. Green, blue, purple, and pink circles denote Ga, Al, N and H atoms, respectively. The reconstructed surface with Ga-H bond and H-terminated N adatom (Nad-H + Ga-H) is shown.
Download figure:
Standard image High-resolution imageIn order to discuss surface structural stability, we calculate the absolute surface energy using the wedge-shape geometry technique.
27,28) In the case of GaN layers on a AlN(0001) surface, we calculate the absolute surface energy  from the absolute energies for bottom-passivated surfaces. Therefore,
from the absolute energies for bottom-passivated surfaces. Therefore,  is defined as
is defined as
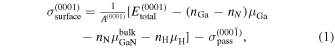
where  is the surface area per unit cell of the AlN(0001) plane,
is the surface area per unit cell of the AlN(0001) plane,  is the total energy of the system per unit cell,
is the total energy of the system per unit cell,  is the chemical potential of the i atom, ni
is the number of atoms of i atoms, and
is the chemical potential of the i atom, ni
is the number of atoms of i atoms, and  is the absolute energy of the AlN(000
is the absolute energy of the AlN(000 ) surface calculated in our previous calculations.
18) Furthermore, the adsorption behavior of the Ga adatom on the reconstructed surface is evaluated using the adsorption energy
) surface calculated in our previous calculations.
18) Furthermore, the adsorption behavior of the Ga adatom on the reconstructed surface is evaluated using the adsorption energy  defined as
defined as
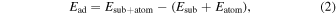
where  and
and  are the total energies of surfaces with and without a Ga adatom, respectively, and
are the total energies of surfaces with and without a Ga adatom, respectively, and  is the total energy of an isolated atom.
is the total energy of an isolated atom.
The calculations are carried out using the extended Tokyo Ab initio Program Package (TAPP), 29,30) which is based on the total energy calculations within the plane-wave pseudopotential approach. The Perdew–Burke–Ernzerhof functional within the generalized gradient approximation is employed for the exchange-correlation energy among electrons. 31) To describe the electron-ion interaction, ultrasoft (norm-conserving) pseudopotentials are used in N (Al, Ga and H) atoms, 32,33) and nonlinear core corrections are adopted for the electrons of Ga-3d orbitals. 34) Both the geometry optimization and the electronic structure calculations are executed by the conjugate-gradient technique. 35,36) The cutoff energies for the valence wave functions and charge densities are 30.25 and 121 Ry, respectively. The k-points sampling of 9 k-points in the 2 × 2 surface unit is used. The settings of k-points sampling and cutoff energies give enough accuracy in the total energies to discuss the relative stability.
3. Results and discussion
Figure 3(a) shows the absolute surface energies of the AlN(0001) surface for various surface structures shown in Figs. 1(a)–1(e) as a function of Al chemical potential. We find that the stable surface structure depends on the Al chemical potential. When the Al chemical potential  −
−  is lower than −2.35 eV, the absolute surface energy of the Al-NH3+3Al-NH2 shown in Fig. 1(e) takes the lowest value. On the other hand, when the Al chemical potential range is −2.35 eV ≤
is lower than −2.35 eV, the absolute surface energy of the Al-NH3+3Al-NH2 shown in Fig. 1(e) takes the lowest value. On the other hand, when the Al chemical potential range is −2.35 eV ≤  −
−  ≤ −1.85 eV, the absolute surface energy of the Nad-H + Al-NH2 shown in Fig. 1(d) is the lowest. The absolute surface energy of the Nad-H + Al-H shown in Fig. 1(c) becomes the lowest for −1.85 eV ≤
≤ −1.85 eV, the absolute surface energy of the Nad-H + Al-NH2 shown in Fig. 1(d) is the lowest. The absolute surface energy of the Nad-H + Al-H shown in Fig. 1(c) becomes the lowest for −1.85 eV ≤  −
−  ≤ −1.00 eV. Since the experimental growth conditions of MOVPE in general correspond to the N-rich conditions, it is likely that the Al-NH3+3Al-NH2 is stable under the experimental conditions.
12) The stabilization of Al-NH3+3Al-NH2 is consistent with the results of the thermodynamic analysis of AlN taking into account the surface reconstruction.
19)
≤ −1.00 eV. Since the experimental growth conditions of MOVPE in general correspond to the N-rich conditions, it is likely that the Al-NH3+3Al-NH2 is stable under the experimental conditions.
12) The stabilization of Al-NH3+3Al-NH2 is consistent with the results of the thermodynamic analysis of AlN taking into account the surface reconstruction.
19)
Fig. 3. (Color online) Calculated the absolute surface energies of (a) AlN(0001) surface for various surface structures in Figs. 1(a)–1(e) as a function of Al chemical potential, and (b) one, (c) two, and (d) three-bilayer of GaN on AlN(0001) surface for various surface structures in Figs. 1(f)–1(j) as a function of Ga chemical potential. The value of hydrogen chemical potential  EH − 0.57 eV, which corresponds to H2 pressure of 76 Torr at 1323 K (EH is the total energy per atom for H2 molecule) in Ref. 12 is considered.
EH − 0.57 eV, which corresponds to H2 pressure of 76 Torr at 1323 K (EH is the total energy per atom for H2 molecule) in Ref. 12 is considered.
Download figure:
Standard image High-resolution imageFigures 3(b)–3(d) show the absolute surface energies of n layers of GaN on AlN(0001) surface for various surface structures shown in Figs. 1(f)–1(j) as a function of Ga chemical potential. It is also found that the stable surface structure depends on Ga chemical potential. When the Ga chemical potential  −
−  is lower than −0.6 eV, the absolute surface energy of the Nad-H + Ga-NH2 shown in Fig. 1(h) takes the lowest value. On the other hand, when the Ga chemical potential range is −0.6 eV ≤
is lower than −0.6 eV, the absolute surface energy of the Nad-H + Ga-NH2 shown in Fig. 1(h) takes the lowest value. On the other hand, when the Ga chemical potential range is −0.6 eV ≤  −
−  ≤ −0.1 eV, the absolute surface energy of Nad-H + Ga-H shown in Fig. 1(g) is the lowest. The absolute surface energy of the Ga bilayer shown in Fig. 1(j) becomes the lowest for −0.1 eV ≤
≤ −0.1 eV, the absolute surface energy of Nad-H + Ga-H shown in Fig. 1(g) is the lowest. The absolute surface energy of the Ga bilayer shown in Fig. 1(j) becomes the lowest for −0.1 eV ≤  −
−  Therefore, the Nad-H + Ga-NH2 and Nad-H + Ga-H are stabilized over the wide range of Ga chemical potential. These results are consistent with the surface structural stability for the GaN(0001) surface.
17) The calculated absolute surface energies for the surfaces corresponding to the MOVPE growth such as the Nad-H + Ga-NH2 and Nad-H + Ga-H are ranging from 0.12 to 0.15 eV Å−2, which is only 0.04 eV Å−2 higher than that of the reconstructed GaN(0001) surfaces.
17) Here, we note that the absolute surface energies of the Nad-H + Ga-NH2 and Nad-H + Ga-H increase by at most 0.005 eV Å−2 even when the number of GaN layers increases up to three bilayers and these values are close to the absolute surface energy of the Al-NH3+3Al-NH2. It is thus concluded that the surface stability of the GaN thin films on the AlN(0001) surface is independent of the thickness of the GaN layer and the surface stability hardly affects the self-limiting growth of GaN on a AlN(0001) surface.
Therefore, the Nad-H + Ga-NH2 and Nad-H + Ga-H are stabilized over the wide range of Ga chemical potential. These results are consistent with the surface structural stability for the GaN(0001) surface.
17) The calculated absolute surface energies for the surfaces corresponding to the MOVPE growth such as the Nad-H + Ga-NH2 and Nad-H + Ga-H are ranging from 0.12 to 0.15 eV Å−2, which is only 0.04 eV Å−2 higher than that of the reconstructed GaN(0001) surfaces.
17) Here, we note that the absolute surface energies of the Nad-H + Ga-NH2 and Nad-H + Ga-H increase by at most 0.005 eV Å−2 even when the number of GaN layers increases up to three bilayers and these values are close to the absolute surface energy of the Al-NH3+3Al-NH2. It is thus concluded that the surface stability of the GaN thin films on the AlN(0001) surface is independent of the thickness of the GaN layer and the surface stability hardly affects the self-limiting growth of GaN on a AlN(0001) surface.
In order to clarify the thickness dependence of the behavior of the Ga adatom, the adsorption-desorption behavior of the Ga adatom for the reconstructed surfaces is examined. Figure 4 shows the adsorption energy of the Ga adatom on n layers of GaN on a AlN(0001) surface as a function of the GaN film thickness. For the AlN(0001) surface corresponding to n = 0, the calculation is performed for the Al-NH3+3Al-NH2 shown in Fig. 1(e). On the other hand, for n layers of GaN on AlN(0001) surfaces with n = 1,2,3, the adsorption of the Ga adatom on the Nad-H + Ga-NH2 and Nad-H + Ga-H shown in Figs. 1(h) and 1(g), respectively, is examined. In the case of a Ga adatom on a AlN(0001) surface, we find that the surface structure with H2 desorption is the most stable atomic configuration. Thus, the adsorption energy of the Ga adatom is calculated taking account of the free energy of the H2 molecule expressed as,
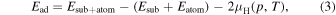
where  0.57 eV (
0.57 eV ( is the total energy per atom for H2 molecule). Here, the value of
is the total energy per atom for H2 molecule). Here, the value of  eV corresponds to the gas phase chemical potential (per atom) of the H2 molecule at p = 76 Torr and T = 1323 K according to Ref. 12 is obtained on the basis of statistical mechanics.
37) We find that the adsorption energy of the Ga adatom on the AlN(0001) surface is smaller than those on the GaN layer on the AlN(0001) surface. The stabilization of the Ga adatom on the Al-NH3+3Al-NH2 surface for n = 0 is due to the formation of three stable Ga-N bonds. On the other hand, for GaN layers on AlN(0001) surface, the Ga adatom forms one Ga-N and one Ga-Ga bond (two Ga-N and one Ga-Ga bonds) for the Nad-H + Ga-H (Nad-H + Ga-NH2) regardless of the number of GaN layers. Therefore, the adsorption energy of the Ga adatom for n
eV corresponds to the gas phase chemical potential (per atom) of the H2 molecule at p = 76 Torr and T = 1323 K according to Ref. 12 is obtained on the basis of statistical mechanics.
37) We find that the adsorption energy of the Ga adatom on the AlN(0001) surface is smaller than those on the GaN layer on the AlN(0001) surface. The stabilization of the Ga adatom on the Al-NH3+3Al-NH2 surface for n = 0 is due to the formation of three stable Ga-N bonds. On the other hand, for GaN layers on AlN(0001) surface, the Ga adatom forms one Ga-N and one Ga-Ga bond (two Ga-N and one Ga-Ga bonds) for the Nad-H + Ga-H (Nad-H + Ga-NH2) regardless of the number of GaN layers. Therefore, the adsorption energy of the Ga adatom for n
 1 hardly (within 0.05 eV) depends on the number of GaN layers. It is thus indicated that the self-limiting growth of GaN layers occurs due to the suppression of the Ga adatom for GaN layers with n
1 hardly (within 0.05 eV) depends on the number of GaN layers. It is thus indicated that the self-limiting growth of GaN layers occurs due to the suppression of the Ga adatom for GaN layers with n
 1 on a AlN (0001) surface.
1 on a AlN (0001) surface.
Fig. 4. (Color online) Calculated adsorption energies of Ga adatom on (a) the Al-NH3+3Al-NH2 (for n = 0) shown in Fig. 1(e) and the Nad-H + Ga-H (for n = 1–3) shown in Fig. 1(g), and (b) the Al-NH3+3Al-NH2 (for n = 0) shown in Fig. 1(e) and the Nad-H + Ga-NH2 (for n = 1–3) shown in Fig. 1(h) as a function of the GaN film thickness n.
Download figure:
Standard image High-resolution imageFigure 5 shows the schematic images for possible mechanisms of the self-limiting growth of GaN layers on the AlN(0001) surface obtained in this study. Since the surface stability is hardly dependent on the GaN thickness, the growth is simply discussed on the basis of adsorption behavior. The Ga adatom easily adsorbs on the AlN(0001) surface, and therefore the growth of the GaN layer can proceed until the formation of one bilayer GaN on the AlN(0001) surface. After the formation of one bilayer GaN, owing to larger adsorption energy compared with the AlN(0001) surface, it is expected that the Ga adatom on GaN layers easily desorbs from the surface during the surface migration. Therefore, the growth of GaN layers after one GaN bilayer on the AlN(0001) surface is suppressed by relatively large adsorption energies leading to the self-limiting growth in the MOVPE.
12) Although detailed growth kinetics such as surface lifetime and diffusion length of the Ga adatom should be verified, the difference in the behavior of the Ga adatom could affect the growth of GaN layers on the AlN(0001) surface. The mechanism proposed in this study will be supported by further investigations of the surface stability and adsorption behavior on  planes, in which two-bilayer GaN are formed on AlN
planes, in which two-bilayer GaN are formed on AlN  surface by the MOPVE.
12)
surface by the MOPVE.
12)
Fig. 5. (Color online) Schematic images for the mechanism for self-limiting growth of GaN layers on AlN(0001) surfaces.
Download figure:
Standard image High-resolution image4. Conclusions
We have theoretically investigated the thickness dependence of GaN layers on the surface structural stability and surface energy and the adsorption behavior of a Ga adatom in n layers of GaN grown on a AlN(0001) surface based on first-principles calculations. We found that the thickness of the GaN layer on the AlN(0001) surface hardly affects the absolute surface energy. Furthermore, the adsorption behavior of the Ga adatom on the AlN(0001) surface is easier than that on GaN layers on a AlN(0001) surface. The calculated adsorption energies suggest that the stability of GaN layers on a AlN(0001) surface hardly affects the self-limiting growth. On the other hand, the adsorption of a Ga adatom on n bilayer GaN on AlN(0001) surfaces can be suppressed, leading to self-limiting growth. The calculated results not only provide some insights for understanding the self-limiting growth of GaN layers on AlN(0001) surfaces but also give an impetus for further theoretical and experimental studies.
Acknowledgments
This work was partially supported by JSPS KAKENHI (Grant No. JP20K05324) and CREST-JST (Grant No. JPMJCR16N2). One of the authors (TA) acknowledges the Collaborative Research Program, which is adopted by Research Institute for Applied Mechanics (RIAM) at Kyushu University. We thank computational resources provided by the facilities at the Research Institute for Information Technology (RIIT) at Kyushu University and the Research Center for Computational Science (RCCS) at the National Institutes of Natural Sciences (Project: 22-IMS-C052).






