1. Introduction
Density matrices play a key role in both quantum mechanics and classical treatment of mixed states [
1], as for instance in the characterization of the second-order polarization properties of electromagnetic waves [
2,
3]. In this paper, the concepts of
discriminating decomposition,
intrinsic density matrix,
sources of purity (population and correlation asymmetry),
intrinsic Stokes parameters,
degree of randomness and
nonregularity are introduced and analyzed in terms of certain types of asymmetry exhibited by density matrices representing
n-dimensional systems. The fact that these notions have proven to be very fruitful for the study and interpretation of polarization density matrices (three-dimensional systems), supports their generalization to
n-dimensional (
nD) density matrices. The sections of the paper are organized in the following manner. Main notations and the framework for the decompositions of a density matrix are introduced below, within the present introductory section. The concepts of
n-dimensional Stokes parameters and Bloch vector are formulated in
Section 2, as required for some results presented in further sections.
Section 3 is devoted to the discriminating decomposition of a density matrix into a convex sum of three density matrices, namely the pure, the fully random (maximally mixed), and the discriminating components; the asymmetry features of the last one determining critical aspects of the physical properties of the whole density matrix. Appropriate parameters characterizing the degree of purity (statistical asymmetry) and randomness (statistical symmetry) are considered in
Section 4, which together with the notion of the intrinsic density matrix introduced in
Section 5, lead to the definition in
Section 6 of two complementary sets of invariant descriptors of asymmetry, namely the indices of population asymmetry and the intrinsic coherences, whose contributions to the overall purity of the state are studied in
Section 7. By taking advantage of the results of the previous sections, the concept of nonregularity of a density matrix is introduced in
Section 8, where its intimate link to the correlation asymmetry and to the chiral properties of the discriminating component is shown. Finally,
Section 9 includes a summary and discussion on the main results presented.
Let us consider an n-dimensional system whose state is characterized by a set of n random variables that can be arranged into a vector of the n-dimensional complex vector space , where the superscript “T” indicates transpose. In the special case that do not fluctuate (i.e., the vector state v is fixed), such a state is pure. Nevertheless, in general, uncertainties or fluctuations on the components of v should be considered, and the corresponding mixed state, which necessarily involves a certain increase of symmetry, is represented by the associated density matrix ρ whose elements are the ensemble averages over the realizations of the components of v.
From a mathematical point of view, a given
n×
n matrix
ρ can be considered a density matrix if and only if
ρ is a trace-normalized positive semidefinite Hermitian matrix, i.e.,
,
(where the dagger indicates conjugate transpose and “tr” stands for the trace), while the real
n eigenvalues of
ρ are nonnegative. Therefore,
ρ can always be expressed as
, where
U is a unitary matrix and
is the diagonal matrix whose diagonal elements are the eigenvalues of
ρ taken in decreasing order
. The diagonalization of
ρ leads to its
spectral decomposition
where ⊗ stands for the Kronecker product,
are the unit eigenvectors of
ρ (which in turn are the vector-columns of
U, and represent the pure eigenstates of
ρ) and
are diagonal matrices whose only nonzero component is
. By denoting
and considering an arbitrary generalized basis of
, being composed of (a) a set of
r independent unit vector states
generating
(
being the subspace of
generated by the
r eigenvectors
with corresponding nonzero eigenvalues
), and (b) a set of
independent unit vector states
generating
(
being the subspace of
generated by the
eigenvectors
with corresponding zero eigenvalues
), the density matrix
ρ can be expressed as a convex sum of the
r pure density matrices
, through the
arbitrary decomposition of
ρ [
4,
5,
6,
7,
8].
From a statistical point of view, the most “symmetric” state is represented by ( being the n×n identity matrix, so that, the n eigenvalues of are equal to ). Conversely, the most “asymmetric” situation corresponds to a pure density matrix , which is characterized by the fact that it has a single nonzero eigenvalue .
2. nD Stokes Parameters and Bloch Vector
Certain results to be considered in further sections concerning invariant descriptors of the asymmetry properties of a density matrix
ρ are closely linked to the concept of
nD Stokes parameters, which are defined as the (real) coefficients
of the expansion of
ρ in terms of the basis of Hermitian matrices composed of the identity matrix
together with the
generalized Pauli matrices
(also called generalized Gell-Mann matrices) [
9]
where the set
of the elements of the Lie algebra of SU(
n) is composed of the union of (a)
symmetric (nondiagonal) matrices
whose elements are zero except for
; (b)
antisymmetric matrices
whose elements are zero except for
, and (c) the
diagonal matrices.
The
nD Stokes parameters
, together with
are the components of the
nD normalized Stokes vector
. Note that the non-normalized version
Φ (coherency matrix) of
ρ is
, with
, which is equivalent to using the non-normalized form of the Stokes vector. The
nD Bloch vector (or coherence vector [
9]) associated with
ρ is
[
9,
10,
11,
12]. Here we have followed the criterion of Byrd and Khaneja [
9] for the definition of parameters
, in such a manner that the absolute value
of the Bloch vector equals 1 for pure states and, as shown in
Section 4, in general coincides with the degree of purity of the state represented by
ρ.
3. Discriminating Decomposition of a Density Matrix
Given an
nD (
n-dimensional) density matrix
ρ, its spectral decomposition (1) can be rearranged into the
characteristic decomposition (also called trivial decomposition) [
4]
where the coefficients are determined by the
indices of purity (hereafter IPP) [
13], defined as follows in terms of the ordered eigenvalues of
ρ.
By grouping the addends of (5) involving
for
into an aggregate component
, the characteristic decomposition becomes the
discriminating decomposition
which provides an expansion of
ρ into a convex composition of the density matrices
,
and
, which are associated, respectively, with the
pure component (which has a single nonzero eigenvalue and is generated by the single eigenstate
), the
discriminating component (whose peculiar features will be analyzed in
Section 9), and the
fully random (or unpolarized) component
, where
is the identity matrix, which corresponds to a maximally mixed state, i.e., to an equiprobable mixture of the
n orthonormal eigenstates of
ρ. The IPP, which determine the coefficients of the characteristic and discriminating decompositions of
ρ is a set of
invariant parameters that provide complete quantitative information on the structure of purity of
ρ and satisfy the nested inequalities
[
13]. The 3D and 4D formulations of the IPP have proven to be useful to address certain problems in polarization optics [
7,
14,
15].
As the larger IPP take consecutively their maximal values equal to 1 (
), the number of nonzero eigenvalues is reduced correspondingly from
n to
r (with
), that is to say, the
upper dimensions collapse because the number of nonvanishing components of the arbitrary and characteristic decompositions becomes
r, and the system can be treated mathematically as having
r effective dimensions. Nevertheless, as shown in
Section 4, the
extra dimensions (corresponding to
, also called the null space of
ρ) have a non-neutral effect on the overall purity of
ρ.
4. Degrees of Purity and Randomness of a Density Matrix
A proper overall measure of the degree of purity (or degree of asymmetry) of a state
ρ is given by [
16,
17]
where
stands for the magnitude of the associated
nD Bloch vector (see
Section 2).
gives a measure of the distance from a state
ρ to a maximally mixed one (fully random) and can also be expressed as follows in terms of the IPP [
13],
As a counterpart of
, the distance from the system to a pure one is given by the degree of randomness (or degree of statistical symmetry), which we define as:
Pure systems (i.e.,
), are characterized by
, or equivalently
, which correspond to the case where all the IPP take their maximal values
. Intermediate values
are taken by
for mixed states, while the minimal value
corresponds to the limiting case of maximally mixed states (equiprobable mixtures of the eigenstates), which are also characterized by
and
. Therefore, the expressions of
and
in terms of the IPP make explicit the role played by
in the quantitative structure of purity of
ρ; that is to say, each
leads to a particular contribution
/[(
n − 1)
k(
k + 1)] to
, and the lower and upper values of each
are limited by
and
respectively
. Observe also that, although the number
of IPP equal to 1 (
) entails that the apparent effective dimensions of the system are
r instead of
n (i.e., the last
eigenvalues of
ρ are zero), the apparent excess of dimensions results in a significant contribution to purity. This interesting feature has been studied in Ref. [
18] for the particular case of 3D polarization matrices.
The fact that purity is realized if and only if
motivated use of the term
purity of
ρ for the quantity
[
19]. Maximally mixed states satisfy
, so that
. Nevertheless, an interesting feature of using
instead of
as a measure of the degree of purity is that it takes the more natural limiting value
for maximally mixed states (maximal statistical symmetry). In addition, the overall measure of purity provided by
can be expressed, as in (9), as a weighted square average of the IPP, which in turn provides detailed and complete quantitative information on the structure of purity of
ρ. The parameter
was first introduced by Samson under the scope of ultra low-frequency magnetic fields [
16], and later by Barakat [
17] (with a different, but equivalent mathematical expression).
was also considered implicitly by Byrd and Khaneja [
9] as the magnitude of the coherence vector (or Bloch vector) associated with an
nD density matrix. The ability of
to represent the degree of polarization (or degree of polarimetric purity) for electromagnetic waves, as well as some important features, have been studied by Setälä et al. [
18,
20,
21], Luis [
22] and by Gil et al. [
4,
23,
24]. Furthermore,
was independently introduced by Gil and Bernabéu as the depolarization index [
25] associated with Mueller matrices representing the transformation of polarization states by the action of a material medium.
Another well-known measure of purity is the von Neumann entropy,
Note that, as suggested by Cloude for polarization density matrices [
26], although the Napierian logarithm (ln) is commonly used for the definition of the von Neumann entropy, the use of the base
n logarithm for the definition of the entropy of
nD density matrices has the peculiarity of restricting the values of
to the range
. Observe also that, while
does not have an analytic expression as a function of
(or
), the fact that
can be expressed in terms of the IPP [
13] implies that
admits an analytic expression in terms of the IPP
. Maximal entropy
corresponds to a maximally mixed state (
, i.e.,
), while the minimum achievable value
is reached for pure states (
, i.e.,
). The concept of von Neumann entropy has been considered under the context of polarization optics for 2D, 3D and 4D density matrices in a number of works, like in Refs. [
2,
27,
28,
29,
30,
31,
32,
33,
34,
35], as well as its comparison to the degree of polarization [
2] and to the depolarization index [
32,
33,
35].
5. The Intrinsic Density Matrix
Given a density matrix
ρ, it has
quantities that are invariant with respect to unitary similarity transformations
(with
V unitary). An interesting set of such invariant quantities is that constituted by the IPP [
13] because they determine the quantitative (but not qualitative) structure of purity in a hierarchical and meaningful manner. To get a more qualitative view of the information contained in
ρ, it is also interesting to explore its invariants with respect to changes of the
n-dimensional Cartesian reference frame taken for its representation. Such changes correspond to orthogonal similarity transformations
, so that the density matrix of a given physical system adopts a particular form for each Cartesian coordinate system
considered. Among them, the
intrinsic reference frame is defined as the one for which the real part
of the corresponding form
of the same state that is represented by
ρ with respect to
becomes diagonal,
, with
. Observe that, from the very definition of the density matrix, the equalities
are satisfied. The transformation from
ρ to
through the rotation of the coordinate system from
to
is performed by means of the corresponding orthogonal similarity transformation
, where
is a proper orthogonal matrix (
,
). Therefore, the intrinsic density matrix
has the peculiar form
where
N, whose components are denoted by
(with
depending on whether
is an odd or even number respectively), is an antisymmetric matrix that encompasses all the imaginary part of
. The coefficient
in the definition of
N and the sign coefficient
ε in its components have been introduced for the sake of consistency with the components of the spin vector of polarization density matrices [
36,
37,
38].
The number
l of scalar real invariants involved in
ρ with respect to arbitrary
n-dimensional rotations of the Cartesian coordinate system is equal to the number
of real variables of
ρ (recall that it is Hermitian and trace-normalized) minus the number
of parameters (angles) associated with an
n×
n orthogonal matrix, which results in
, i.e., the
n intrinsic populations , with the restriction
, plus the
intrinsic coherences (hereafter denoted as IC). Note that, as usual when dealing with density matrices of quantum mechanical systems, the terms
populations and
coherences are used in this work to refer to the diagonal and off-diagonal elements of
ρ respectively [
39], while the adjective
intrinsic is used for quantities derived from the intrinsic density matrix. It is remarkable that in polarization optics
the pseudovector
defined from the elements of
N is precisely the spin density vector of the state represented by the corresponding 3×3 polarization density matrix
ρ [
36,
37]. Nevertheless, the fact that the number
of intrinsic coherences equals the dimensions
n is not a general property but it is a genuine feature of three-dimensional systems. This is the reason why the generalization of the concept of spin density vector, defined for the case
, to density matrices with dimensions
is not possible in a consistent manner.
The intrinsic representation of a given ρ has the peculiar feature that the Stokes parameters corresponding to the symmetric (nondiagonal) generators vanish, and therefore the intrinsic Bloch vector contains no more than nonzero Stokes parameters.
Since ρ is positive semidefinite, and despite the fact that it is characterized by the nonnegativity of its four eigenvalues, the nonnegativity of its principal minors implies certain restrictions on the values of and , among which we can mention and , which will be useful in further analyses.
6. Population and Correlation Asymmetries. Intrinsic Stokes Parameters
As with the
IPP,
, defined from the
n eigenvalues of
ρ, we introduce the
indices of population asymmetry (hereafter IP) defined from the
n intrinsic populations of
ρ in the following manner.
The IP satisfy the nested inequalities , and provide complete information on the structure of the population asymmetry of the system represented by ρ. A state for which all the intrinsic populations are equal (full population symmetry, i.e., ) is characterized by , while the maximal population asymmetry is reached when , , i.e., .
In analogy to the names used in polarization optics, we call the set composed of the IP plus the IC, the
components of purity (CP) of
ρ. Therefore, the CP constitutes a proper complete set of
l rotational invariants of
ρ. To go deeper into the physical significance of the CP, let us consider the expansion of the intrinsic density matrix
in terms of the SU(
n) generators
introduced in
Section 2, which adopts the form
where the intrinsic Stokes parameters (i.e., the set of Stokes parameters corresponding to the intrinsic representation
of
ρ) are given by the set composed of the
intrinsic population-Stokes parameters
together with the
intrinsic correlation-Stokes parameters
showing the remarkable result that, up to respective coefficients
,
are not other than the intrinsic Stokes parameters
corresponding to the diagonal generators
, while the intrinsic correlation-Stokes parameters
(associated with the antisymmetric generators
) are directly linked to the intrinsic coherences
. The difference between the physical nature of
and
, together with the fact that a number of
Stokes parameters become zero in the intrinsic representation, suggests the appropriateness of the arrangement of the
nonzero intrinsic Stokes parameters in the form of the following upper triangular
Stokes parameters matrix
whose elements are denoted as
with
,
, and
; in such a manner that the intrinsic population-Stokes parameters are arranged along the diagonal of matrix
S, while the intrinsic correlation-Stokes parameters are arranged in its upper off-diagonal part. Obviously, when the non-normalized version
of the coherency matrix is considered, then the corresponding (non-normalized) Stokes parameters matrix is given by
. Observe also that
.
In summary, the information contained in the density matrix ρ can be grouped into three kinds of parameters of different nature, (a) the angles determining the orthogonal matrix that performs the rotation transformation from the intrinsic reference frame to the actual one; (b) the IP, , or equivalently, the intrinsic population-Stokes parameters, and (c) the intrinsic coherences, , or equivalently, the intrinsic correlation-Stokes parameters.
7. Structure of Purity of a Density Matrix
The Frobenius norm
of
ρ is invariant under unitary similarity transformations (hence it is also invariant under orthogonal similarity transformations), and can be expressed as follows in terms of the CP
and therefore the degree of purity
adopts the following expression
that is,
where two separate sources of purity are identified, namely the
degree of population asymmetry and the
degree of correlation asymmetry . Both descriptors are restricted to the intervals
and
, whose limits correspond to the following kinds of states,
when the state has full population symmetry, , so that the intrinsic density matrix takes the form . Note that does not necessarily imply that , i.e., full population symmetry is compatible with a certain degree of correlation asymmetry .
when the state has full population asymmetry , , i.e., , which in turn implies and .
when the state lacks correlation asymmetry, in which case and all asymmetry is originated by . The complete interval of values for are achievable, depending on the relative values of the intrinsic populations.
corresponds to pure states
with maximal correlation asymmetry, in which case
necessarily adopts the form,
with
. It is remarkable that, when dealing with polarization density matrices
,
corresponds to a circularly polarized pure state [
6], characterized by the fact that its spin density vector takes its maximum achievable magnitude (maximal degree of circular polarization) and lies along the intrinsic axis
, normal to the plane
containing the polarization ellipse of the state.
Pure states are characterized by
, where the full purity is reached through the balanced contributions of the degrees of population and correlation asymmetry, showing that the concept of purity of a state is identified with such a composition of asymmetries, while, as expected, the symmetry appears as a result of the randomness. An analysis of these features for the case
can be found in [
38]. For a pure state (
, i.e.,
),
has the generic form
in such a manner that all the physical information is concentrated into the 2×2 upper-left corner of the intrinsic density matrix, with
and
. Thus, a pure state admits a simple representation with respect to its effective intrinsic reference frame
through the
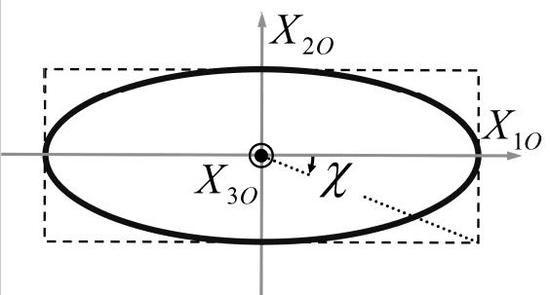
intrinsic polarization ellipse (where the term polarization is used in the generic sense of asymmetry and not specifically for polarized light) (
Figure 1). The only free parameter of a pure state in its intrinsic representation is the ellipticity angle
χ, which determines the shape of the polarization ellipse. In particular,
for linearly polarized states
,
for left-handed/right-handed (anticlockwise/clockwise handedness from the point of view of the receiver) circularly polarized states
respectively.
Thus, any pure state can be represented with respect to its effective intrinsic reference frame
and exhibits a well-defined handedness
H, given by
(with the convention
for
),
for right-handed states and
for left-handed ones. Observe that
H is an intrinsic property that involves chirality. In fact, by considering the spectral decomposition (1) of a density matrix
ρ, all the eigenstates
have well-defined and intrinsic respective handedness, so that it can properly be said that
ρ involves intrinsic chiral properties associated with those of its eigenstates. For a given pure state
its chirality vanishes when
, while from an overall point of view,
ρ carries non-vanishing chirality as long as at least one of the eigenstates
has nonzero spin (i.e.,
, or, equivalently
). The features of the ellipticity angles and the associated spin vectors of generic sets
of orthonormal states for 3D polarization density matrices have been studied in [
40].
As the larger IP, , take consecutively their maximal values equal to 1, the effective dimensions of the intrinsic density matrix are reduced correspondingly from n to r (with ), is the number of IPP equal to 1 (), that is to say, the last intrinsic populations become zero, while the elements of the last rows and columns of ρ also become zero.
8. The Concept of Nonregularity of a Density Matrix
The discriminating decomposition (7) of a density matrix
ρ is formulated as a convex composition of three density matrices, namely (1) the pure component
, whose intrinsic form
has been described in Equation (22); (2) the symmetric component
(also called fully random, or unpolarized component), and (3) the discriminating component
. In general,
has a complicated structure, and it can have different interesting forms. When
is a real matrix, then it can be expressed as a weighted sum of density matrices, each one corresponding to a respective equiprobable mixture of a number of, 2, 3,… and
n-1 mutually orthogonal pure states with zero spin
where the diagonalization matrix
Q is orthogonal. Observe that the fact that
is a real matrix, (hence it is symmetric and can be diagonalized through the orthogonal matrix
Q) does not imply that the matrix
U that diagonalizes
ρ is necessarily a real matrix; that is, there are cases for which there is degeneracy for certain eigenvalues of
so that it can be diagonalized either by means of
U (in general, complex-valued) or
Q (real-valued). In summary, from Equation (7),
is in general complex-valued (in which case
U is not real-valued), so that we can distinguish between
regular states, defined as those where either
(in which case the coefficient of
in the discriminating decomposition (7) vanishes), or
is a real matrix, and
nonregular states, for which
and
[
7,
41]. Thus, nonregularity occurs when the correlation asymmetry of
is nonzero,
, while regularity appears as the limiting situation where
(or, alternatively, where the equality
is satisfied). Consequently, the maximal achievable value for
should be inspected in order to define a generalized degree of nonregularity (note that the version for
was already defined for density polarization matrices in previous work [
41]).
The discriminating density matrix
can be represented with respect to its own intrinsic reference frame
(observe that, in general,
is different from the intrinsic reference frame
of
ρ). The off-diagonal elements of the intrinsic form
are purely imaginary and their absolute values, together with the populations
, are limited by the constraints of nonnegativity of all principal minors of
, in such a manner that the maximization of
requires that
has the form
and therefore,
. Since
is invariant under orthogonal similarity transformations of
it follows that
and we deduce that the degree of correlation asymmetry of the discriminating component is limited by
, where the minimum
corresponds to regular states, and otherwise,
ρ is a nonregular state, with a maximum
for states with maximal nonregularity, hereafter called
perfect nonregular states.
The above results support the definition of the degree of nonregularity
of a discriminating state
as
, with
for regular discriminating states and
for perfect nonregular discriminating states, and by considering the weight
of the component
in the discriminating decomposition (7), we define the
degree of nonregularity of a density matrix
ρ as
so that regular states are those that either satisfy
or whose discriminating component is regular (i.e.,
lacks correlation asymmetry), while the degree of nonregularity of
ρ is that of
but scaled by the coefficient
, and therefore
ρ represents a perfect nonregular state
when
ρ itself has the form of a discriminating density matrix
with
.
As discussed in
Section 7, nonzero correlation asymmetry of a given density matrix
ρ involves necessarily certain chirality associated with the eigenstates of
ρ, and by noting that the existence of nonzero correlation asymmetry of the discriminating component
of
ρ implies nonregularity, we find an interesting and subtle link between the concepts of chirality and nonregularity of a given
ρ. Observe also that the complete interval of values
is achievable for regular states; in particular
when
ρ is a real matrix (hence regular) and
when
ρ represents a circularly polarized pure state. Thus,
may be interpreted as a measure of the degree of chirality of the state
ρ, while the degree of chirality
of the discriminating component determines the degree of nonregularity of
ρ.
The definition of
generalizes the results already obtained for the case
in previous works dealing with polarization density matrices [
7,
41], which have been successfully applied to the characterization of polarization of evanescent waves [
42] and tightly focused fields [
43].
9. Discussion and Conclusions
There are many problems in physics whose formulation becomes strongly simplified when a specific reference frame is used. A well-known case is the definition of the tangential and normal components of the acceleration associated with the classical motion of a particle by means of the choice of an intrinsic coordinate system for each point of the trajectory. In this work, the definition of an intrinsic coordinate system for each given
n-dimensional density matrix
ρ is exploited in order to define a set of quantities (the components of purity -CP- of the state) that provide complete information on the rotational invariant properties associated with
ρ in a hierarchical and meaningful manner. In fact, it is found that the CP coincide, up to respective simple coefficients, with the
n-dimensional Stokes parameters of the state in its intrinsic representation. These results generalize the obtainment of the six intrinsic Stokes parameters for 3D polarization states, whose physical interpretation is as simple as the intensity, the degree of linear polarization, the degree of directionality and the three intrinsic components of the spin density vector of the state [
6,
37]. Thus, any polarization density matrix can be conceived as the intrinsic one (linked in a very simple way to the intrinsic Stokes parameters) and a spatial rotation of the Cartesian reference frame (three angular parameters).
In the general case of a density matrix
ρ representing an
n-dimensional mixed state, which depends on up to
free parameters, the situation is more involved than for 2D or 3D density matrices and the generalization is not straightforward; in fact, as described in
Section 5, when
the imaginary parts of the off-diagonal elements of
ρ cannot be longer interpreted as the components of the spin density vector.
Regarding the invariants of
ρ with respect to unitary similarity transformations
, a parametrization based on the
indices of purity (IPP) was defined in previous work [
13]. The IPP,
are constrained by the nested inequalities
and provide, in an optimal and hierarchical manner, quantitative (but not qualitative) information on the structure of purity of
ρ. In fact, the degree of purity
(which represents the degree of statistical asymmetry) can be obtained as a weighted square average of the IPP.
Nevertheless, more detailed and qualitative information can be obtained from ρ through the introduction of the concept of intrinsic density matrix, which leads to the definition of a number of l (with ) invariants of ρ with respect to arbitrary rotations of the n-dimensional Cartesian reference frame, i.e., with respect to orthogonal similarity transformations . In this case, the total number l of invariants defined in this work and called the components of purity (CP) of ρ, can be grouped into two meaningful sets, namely (a) the indices of population asymmetry (IP), , (or, equivalently, the intrinsic population-Stokes parameters) which are constrained by the nested inequalities and provide, in an optimal and hierarchical manner, complete information on the structure of population asymmetry of ρ, and (b) the intrinsic coherences (IC), , (or, equivalently, the intrinsic correlation-Stokes parameters) that provide complete information on the correlation asymmetry of ρ.
From these sets of parameters, two complementary sources of purity, namely the degree of population asymmetry, , and the degree of correlation asymmetry, , are defined as respective square averages, in such a manner that is, in turn, a weighted square average of and . All the above descriptors are used to analyze the peculiar features of the discriminating decomposition of a given density matrix ρ into a convex sum (or incoherent superposition) of three density matrices, namely (1) a pure one, (2) a maximally mixed one, and (3) a discriminating one that holds certain critical properties of ρ and leads to the definition of the degree of nonregularity, which is determined by the degree of correlation asymmetry of the discriminating component, scaled by the difference between the maximum and minimum IPP of ρ.
It should be stressed that, through the diagonalization of the intrinsic density matrix, the IPP can be calculated from the components of purity, which agrees with the obvious fact that orthogonal matrices constitute a type of unitary matrices (those that are real-valued), i.e., all invariants under transformations (with U unitary), are invariants under (with Q orthogonal). Therefore, the set of CP is complete, because parametrizes all the l indicated rotational invariants of ρ. Furthermore, the CP (hence, the intrinsic Stokes parameters) are physically meaningful because they satisfy the following properties
- (a)
As shown in Equation (20), the degree of purity is given by a weighted square average of the CP. The degrees of population and correlation asymmetry constitute two complementary sources of purity. Full population asymmetry entails full purity and zero correlation asymmetry , while full correlation asymmetry implies full purity together with a certain amount of population asymmetry , in which case the state can be represented by a circularly polarized state embedded into an n-dimensional space.
- (b)
The indices of population asymmetry are defined in a hierarchical manner , so that implies that the state is maximally mixed, while implies full population asymmetry (or population purity) and full overall purity , in which case the state can be represented by a linearly polarized state embedded into an n-dimensional space.
- (c)
The intrinsic coherences hold all information on the correlations among the random variables that describe the system. Their values are constrained by those of because of the nonnegativity of the principal minors of ρ. Moreover, the inherent chirality associated with the degree of correlation asymmetry, which has its origin in the handedness of the eigenstates of ρ, has been analyzed and characterized.
- (d)
All the information contained in ρ ( free parameters) can be parametrized by an n-dimensional rotation (non-invariant angular parameters) together with the indices of population asymmetry and the intrinsic coherences of ρ.
The general framework introduced provides invariant descriptors for
n-dimensional density matrices that, in turn, have been proven to be fruitful for the study of three-dimensional states of polarization [
4,
6,
7,
13,
23,
24,
27,
28,
30,
36,
37,
38,
40,
41,
42,
43,
44,
45,
46,
47,
48] and of the polarimetric properties of material media [
4,
5,
8,
13,
23,
24,
25,
32,
33,
34,
35,
49,
50,
51], which supports a well-founded expectation for its useful application to
n-dimensional density matrices representing quantum or classical systems.