Microstructural Origins of Nonlinear Response in Associating Polymers under Oscillatory Shear
Abstract
:1. Introduction
2. Simulation Method
2.1. Molecular Dynamics/Monte Carlo Code
2.2. System Properties
2.3. Network Topology
3. Results
3.1. Moduli
3.2. Viscoelastic-Structural Response
3.3. Topological Features
3.4. Aggregate Dynamics
3.5. Repetitive Structures
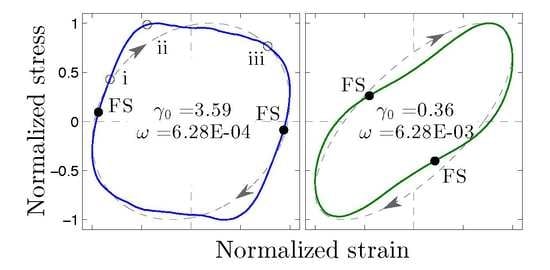
3.6. LAOS and Shear Banding
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hao, J.K.; Weiss, R.A. Viscoelastic and Mechanical Behavior of Hydrophobically Modified Hydrogels. Macromolecules 2011, 44, 9390–9398. [Google Scholar] [CrossRef]
- Kujawa, P.; Wanatabe, H.; Tanaka, F.; Winnink, F.M. Amphiphilic Telechelic Poly (N-Isopropylacrylamide) in Water: From Micelles to Gels. Eur. Phys. J. E 2005, 17, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Sing, M.K.; Wang, Z.-G.; McKinley, G.H.; Olsen, B.D. Celebrating Soft Matter’s 10th Anniversary: Chain Configuration and Rate-Dependent Mechanical Properties in Transient Networks. Soft Matter 2014, 11, 2085–2096. [Google Scholar] [CrossRef] [PubMed]
- Verso, F.L.; Likos, C.N. End-Functionalized Polymers: Versatile Building Blocks for Soft Materials. Polymer 2008, 49, 1425–1449. [Google Scholar] [CrossRef]
- Glass, J.E. Hydrophilic Polymers: Performance with Environmental Acceptability. In Advances in Chemistry Series, 9th ed.; American Chemical Society: Washington, DC, USA, 1996; Volume 248. [Google Scholar]
- Dhandayuthapani, B.; Yoshida, Y.; Maekawa, T.; Kumar, D.S. Polymeric scaffolds in tissue engineering Application: A review. Int. J. Political Sci. 2011, 2011, 290602. [Google Scholar] [CrossRef]
- Wojtecky, R.J.; Meador, M.A.; Rowan, S.J. Using the Dynamic Bond to Access Macroscopically Responsive Structurally Dynamic Polymers. Nat. Mater. 2011, 10, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, S.; Bassett, D.S.; Winkelstein, B.A. Stretched-Induces Network Reconfiguration of Collegen Fibres in the Human Facet Capsular Ligament. J. R. Soc. Interface 2016, 13, 20150833. [Google Scholar]
- Hawke, L.G.D.; Amandi, M.; Goldansaz, H.; van Ryumbeke, E. Viscoelastic properties of linear associating poly (N-Butylacrylate) Chains. J. Rheol. 2016, 60, 297–310. [Google Scholar]
- Zinn, T.; Willner, L.; Lund, R. Telechelic Polymer Hydrogels: Relation between Microscopic Dynamics and Macroscopic Viscoelastic Response. ACS Macro Lett. 2016, 5, 1353–1356. [Google Scholar] [CrossRef]
- Semenov, A.M.; Rubinstein, N. Thermoreversible Gelations in Solutions of Associating Polymers. Macromolecules 1998, 31, 1373–1385. [Google Scholar] [CrossRef]
- Witten, T.A. Associating Polymers and Shear Thickening. J. Phys. 1988, 49, 1055–1063. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A Geometrical Interpretation of Large Amplitude Oscillatory Shear Response. J. Rheol. 2005, 49, 747–758. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Hosoi, A.E.; McKinley, G.H. New Measures for Characterizing Nonlinear Viscoelasticity in Large Amplitude Oscillatory Shear. J. Rheol. 2008, 52, 1427–1458. [Google Scholar] [CrossRef]
- Rogers, S.A.; Erwin, B.M.; Vlassopoulos, D.; Cloitre, M. A Sequence of Physical Processes Determined and Quantified in LAOS: Application to a Yield Stress Fluid. J. Rheol. 2011, 55, 435–458. [Google Scholar] [CrossRef]
- Rogers, S.A.; Erwin, B.M.; Vlassopoulos, D.; Cloitre, M. Oscillatory Yielding of a Colloidal Star Glass. J. Rheol. 2011, 55, 733–752. [Google Scholar] [CrossRef]
- Rogers, S.A.; Lettinga, M.P. A Sequence of Physical Processes Determined and Quantified in Large-Amplitude Oscillatory Shear (LAOS): Application to Theoretical Nonlinear Models. J. Rheol. 2012, 56, 1–25. [Google Scholar] [CrossRef]
- Wilson, M.; Rabinovitch, A.; Baljon, A.R.C. Computational Study of the Structure and Rheological Properties of Self-Associating Polymer Networks. Macromolecules 2015, 48, 6313–6320. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinly, G.H. A Review of Nonlinear Oscillatory Shear Tests: Analysis and Application of Large Amplitude Oscillatory Shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Wyss, H.M.; Miyazaki, K.; Mattsson, J.; Hu, Z.; Reichman, D.R.; Weitz, D.A. Strain-Rate Frequency Superposition: A Rheological Prope of Superposition in Soft Materials. Phys. Rev. Lett. 2007, 98, 238303. [Google Scholar] [CrossRef] [PubMed]
- Hess, A.; Aksel, N. Yielding and Structural Relaxation in Soft Materials: Evaluation of Strain-Rate Frequency Superposition Data by the Stress Decomposition Method. Phys. Rev. E 2011, 84, 051502. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of Entangled Linear Polymer Melts: A Molecular-Dynamics Simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Baljon, A.R.C.; Depuy, T.; Vorselaars, J. Computational Studies of Contact Time Dependence of Adhesive Energy due to Redistribution of the Locations of Strong Specific Interfacial Interactions. Macromolecules 2004, 37, 5800–5806. [Google Scholar] [CrossRef]
- Baljon, A.R.C.; Flynn, D.; Krawzsenek, D. Numerical Study of the Gel Transition in Reversible Associating Polymers. J. Chem. Phys. 2007, 126, 044907. [Google Scholar] [CrossRef] [PubMed]
- Hoy, R.S.; Fredrickson, G.H. Thermoreversible Associating Polymer Networks: I. Interplay of Thermodynamics, Chemical Kinetics, and Polymer physics. J. Chem. Phys. 2009, 131, 224902. [Google Scholar] [CrossRef] [PubMed]
- Amin, D.; Likhtman, A.E.; Wang, Z. Dynamics in Supramolecular Polymer Networks Formed by Associating Telechelic Chains. Macromolecules 2016, 49, 7510–7524. [Google Scholar] [CrossRef]
- Billen, J.; Wilson, M.; Baljon, A.R.C. Shear Banding in Simulated Telechelic Polymers. Chem. Phys. 2015, 142, 7–12. [Google Scholar] [CrossRef]
- Lavrentovich, M.O.; Liu, A.J.; Nagel, S.R. Period Proliferation in Periodic States in Cyclically Sheared Jammed Solids. Phys. Rev. E 2017. [Google Scholar] [CrossRef] [PubMed]
- Sprakel, J.; Spruijt, E.; Cohen Stuart, M.A.; Besseling, N.A.M.; Lettinga, M.P.; van der Gucht, J. Shear Banding and Rheochaos in Associative Polymer Networks. Soft Matter 2008, 4, 1696–1705. [Google Scholar] [CrossRef] [Green Version]
- Manneville, S.; Colin, A.; Waton, G.; Schosseler, F. Wall slip, Shear Banding, and Instability in the Flow of a Triblock Copolymer Micellar Solution. Phys. Rev. E 2007, 75, 061502. [Google Scholar] [CrossRef] [PubMed]
- Lerouge, S.; Decruppe, J.-P.; Olmsted, P. Birefringence Banding in a Micellar Solution or the Complexity of Heterogeneous Flows. Langmuir 2004, 20, 11355–11356. [Google Scholar] [CrossRef] [PubMed]
- Mermet-Guyennet, M.R.B.; Gianfelice de Castro, J.; Habibi, M.; Martzel, N.; Denn, M.M.; Bonn, D. LAOS: The Strain Softening/Strain Hardening Paradox. J. Rheol. 2015, 59, 21–32. [Google Scholar] [CrossRef]
- Lim, H.T.; Ahn, K.H.; Hyun, K. Nonlinear Viscoelasticity of Nanocomposites under Large Oscillatory Shear Flow. J. Rheol. 2013, 57, 767–789. [Google Scholar] [CrossRef]
- Papon, A.; Maribia, S.; Guy, L.; Mpntes, H.; Sotta, P.; Long, D. Unique Non-Linear Behavior of Nanofilled Elastomers: From the Onset of Strain Softening to Large Amplitude Shear Deformations. Macromolecules 2012, 45, 2891–2904. [Google Scholar] [CrossRef]
- Li, S.; Mi, Y.; Wang, X. Superposed Nonlinear Rheological Behavior of Filled Elastomers. J. Rheol. 2017, 61, 409–425. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Winter, P.; Maxey, J.; McKinley, G.H. Large Amplitude Oscillatory Shear of Pseudoplastic and Elastoviscoplastic Materials. Rheol. Acta 2010, 49, 191–212. [Google Scholar] [CrossRef]
- Brian, M.E. Examing the Validity of Strain-Rate Frequency Superposition when Measuring the Linear Viscoelastic Properties of Soft Materuals. J. Rheol. 2010, 54, 187–195. [Google Scholar]
- Hyun, K.; Lim, H.T.; Ahn, K.H. Nonlinear Response of Polypropylene (PP)/Clay Nanocomposites under Dynamic Oscillatory Shear Flow. Korea-Aust. Rheol. J. 2012, 24, 113–120. [Google Scholar] [CrossRef]
- Swan, J.W.; Zia, R.N.; Brady, J.F. Large Amplitude Oscillatory Microrheology. J. Rheol. 2014, 58, 1–41. [Google Scholar] [CrossRef]
- Rogers, S.; Kohlbrecher, J.; Lettinga, M.P. The Molecular Origin of Stress Generation in Worm-Like Micelles, Using a Rheo-SANS LAOS Approach. Soft Matter 2012, 8, 7831–7839. [Google Scholar] [CrossRef] [Green Version]
- Calabrese, M.A.; Wagner, N.J. Wormlike Micelles: Systems, Characterization and Applications; Dreiss, C., Feng, Y., Eds.; Royal Society of Chemistry: London, UK, 2017; pp. 193–235. [Google Scholar]








© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, M.A.; Baljon, A.R.C. Microstructural Origins of Nonlinear Response in Associating Polymers under Oscillatory Shear. Polymers 2017, 9, 556. https://doi.org/10.3390/polym9110556
Wilson MA, Baljon ARC. Microstructural Origins of Nonlinear Response in Associating Polymers under Oscillatory Shear. Polymers. 2017; 9(11):556. https://doi.org/10.3390/polym9110556
Chicago/Turabian StyleWilson, Mark A., and Arlette R. C. Baljon. 2017. "Microstructural Origins of Nonlinear Response in Associating Polymers under Oscillatory Shear" Polymers 9, no. 11: 556. https://doi.org/10.3390/polym9110556