Plasmonic-Induced Transparencies in an Integrated Metaphotonic System
Abstract
:1. Introduction
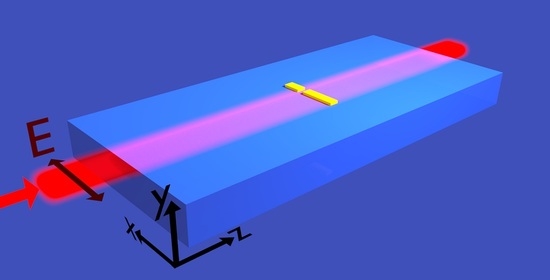
2. Description and Principle of Operation of the System
3. Results
3.1. Single Nanoparticle
3.1.1. Short Nanoparticle
3.1.2. Long Nanoparticle
3.2. Two Nanoparticles
3.2.1. Lateral Shift
3.2.2. Longitudinal Shift
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benson, O. Assembly of hybrid photonic architectures from nanophotonic constituents. Nature 2011, 480, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Chamanzar, M.; Apuzzo, A.; Salas-Montiel, R.; Nguyen, K.N.; Blaize, S.; Adibi, A. On-Chip Hybrid Photonic–Plasmonic Light Concentrator for Nanofocusing in an Integrated Silicon Photonics Platform. Nano Lett. 2015, 15, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light. Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef] [Green Version]
- Dubrovina, N.; Fan, Y.; Roux, X.L.; de Lustrac, A.; Lupu, A. Guided wave metamaterials for integrated optics applications. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Xu, W. Surface plasmon polaritons: Physics and applications. J. Phys. D Appl. Phys. 2012, 45, 113001. [Google Scholar] [CrossRef]
- Pluchery, O.; Vayron, R.; Van, K.M. Laboratory experiments for exploring the surface plasmon resonance. Eur. J. Phys. 2011, 32, 585–599. [Google Scholar] [CrossRef]
- Chamanzar, M.; Xia, Z.; Yegnanarayanan, S.; Adibi, A. Hybrid integrated plasmonic-photonic waveguides for on-chip localized surface plasmon resonance (LSPR) sensing and spectroscopy. Opt. Express 2013, 21, 32086–32098. [Google Scholar] [CrossRef]
- Nezhad, M.P.; Tetz, K.; Fainman, Y. Gain assisted propagation of surface plasmon polaritons on planar metallic waveguides. Opt. Express 2004, 12, 4072–4079. [Google Scholar] [CrossRef]
- Richards, D.; Zayats, A.; Krenn, J.R.; Weeber, J.C. Surface plasmon polaritons in metal stripes and wires. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 739–756. [Google Scholar] [CrossRef]
- Melikyan, A.; Kohl, M.; Sommer, M.; Koos, C.; Freude, W.; Leuthold, J. Photonic-to-plasmonic mode converter. Opt. Lett. 2014, 39, 3488–3491. [Google Scholar] [CrossRef]
- Février, M.; Gogol, P.; Aassime, A.; Mégy, R.; Delacour, C.; Chelnokov, A.; Apuzzo, A.; Blaize, S.; Lourtioz, J.M.; Dagens, B. Giant coupling effect between metal nanoparticle chain and optical waveguide. Nano Lett. 2012, 12, 1032–1037. [Google Scholar] [CrossRef]
- Téllez-Limón, R.; Salas-Montiel, R. Nanowires Integrated to Optical Waveguides; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Tellez-Limon, R.; Blaize, S.; Gardillou, F.; Coello, V.; Salas-Montiel, R. Excitation of surface plasmon polaritons in a gold nanoslab on ion-exchanged waveguide technology. Appl. Opt. 2020, 59, 572–578. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Dai, L.; Jiang, C. Electromagnetically induced transparency in hybrid plasmonic-dielectric system. Opt. Express 2011, 19, 628–637. [Google Scholar] [CrossRef] [Green Version]
- Foroutan, S.; Rostami, G.; Dolatyari, M.; Rostami, A. All-Optical switching in metal nanoparticles plasmonic waveguide using EIT phenomenon. Optik 2017, 132, 291–298. [Google Scholar] [CrossRef]
- Hajshahvaladi, L.; Kaatuzian, H.; Danaie, M. Design and analysis of a plasmonic demultiplexer based on band-stop filters using double-nanodisk-shaped resonators. Opt. Quantum Electron. 2018, 51, 391. [Google Scholar] [CrossRef]
- Yang, A.; Wang, D.; Wang, W.; Odom, T.W. Coherent light sources at the nanoscale. Annu. Rev. Phys. Chem. 2017, 68, 83–99. [Google Scholar] [CrossRef] [PubMed]
- Bermúdez-Ureña, E.; Tutuncuoglu, G.; Cuerda, J.; Smith, C.L.C.; Bravo-Abad, J.; Bozhevolnyi, S.I.; Fontcuberta i Morral, A.; García-Vidal, F.J.; Quidant, R. Plasmonic waveguide-integrated nanowire laser. Nano Lett. 2017, 17, 747–754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koenderink, A.F. Single-photon nanoantennas. ACS Photon. 2017, 4, 710–722. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Li, F.; Qiu, H.; Zhang, Z.; Wang, H.; Min, C.; Du, L.; Li, Z.; Yuan, X. Ultra-broadband on-chip twisted light emitter for optical communications. Light. Sci. Appl. 2018, 7, 18001. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Tuniz, A.; Bickerton, O.; Diaz, F.J.; Käsebier, T.; Kley, E.B.; Kroker, S.; Palomba, S.; de Sterke, C.M. Modular nonlinear hybrid plasmonic circuit. Nat. Commun. 2020, 11, 2413. [Google Scholar] [CrossRef]
- Li, Z.; Kim, M.H.; Wang, C.; Han, Z.; Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Agarwal, A.M.; Lončar, M.; et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces. Nat. Nanotechnol. 2017, 12, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Guo, R.; Decker, M.; Setzpfandt, F.; Gai, X.; Choi, D.Y.; Kiselev, R.; Chipouline, A.; Staude, I.; Pertsch, T.; Neshev, D.N.; et al. High-bit rate ultra-compact light routing with mode-selective on-chip nanoantennas. Sci. Adv. 2017, 3, e1700007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Garrido Alzar, C.L.; Martinez, M.A.G.; Nussenzveig, P. Classical analog of electromagnetically induced transparency. Am. J. Phys. 2002, 70, 37–41. [Google Scholar] [CrossRef] [Green Version]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice Hall: Hoboken, NJ, USA, 1983. [Google Scholar]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photon. 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anisimov, P.M.; Dowling, J.P.; Sanders, B.C. Objectively discerning Autler-Townes splitting from electromagnetically induced transparency. Phys. Rev. Lett. 2011, 107, 163604. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Şahin Kaya, Ö.; Chen, W.; Nori, F.; Yang, L. What is and what is not electromagnetically induced transparency in whispering-gallery microcavities. Nat. Commun. 2014, 5, 5082. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Bozhevolnyi, S.I. Plasmon-induced transparency with detuned ultracompact Fabry-Perot resonators in integrated plasmonic devices. Opt. Express 2011, 19, 3251–3257. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yang, J.; He, X.; Han, Y.; Zhang, J.; Huang, J.; Chen, D.; Xu, S. Active enhancement of slow light based on plasmon-induced transparency with gain materials. Materials 2018, 11, 941. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Hu, X.; Yan, Q.; Zhu, J.; Cheng, H.; Huang, Y.; Lu, C.; Fu, Y.; Gong, Q. Plasmon-induced transparency effect for ultracompact on-chip devices. Nanophotonics 2019, 8, 1125–1149. [Google Scholar] [CrossRef]
- Sun, L.; Wang, J.; Wang, Y.; Liu, H.; Liu, C.; Gao, S. Electromagnetically induced transparency of double-groove shaped plasmonic waveguide. Optik 2015, 126, 2596–2599. [Google Scholar] [CrossRef]
- Shen, X.; Wang, Y.; Chen, Q.; Wu, X. Detuned square ring resonators for multiple plasmon-induced transparencies in metal–insulator–metal waveguide. Appl. Phys. Express 2015, 8, 112201. [Google Scholar] [CrossRef]
- Xiong, C.; Li, H.; Xu, H.; Zhao, M.; Zhang, B.; Liu, C.; Wu, K. Coupling effects in single-mode and multimode resonator-coupled system. Opt. Express 2019, 27, 17718–17728. [Google Scholar] [CrossRef]
- Shen, X.; Wang, Y.; Yan, X.; Yuan, L.; Sang, T. Transmission characteristics and transmission line model of a metal-insulator-metal waveguide with a stub modified by cuts. Appl. Opt. 2016, 55, 6443–6446. [Google Scholar] [CrossRef] [PubMed]
- Ortuño, R.; Cortijo, M.; Martínez, A. Fano resonances and electromagnetically induced transparency in silicon waveguides loaded with plasmonic nanoresonators. J. Opt. 2017, 19, 025003. [Google Scholar] [CrossRef]
- Vyas, H.; Hegde, R. The Fano signature in the optical response of a waveguide-excited compound plasmonic nanoantenna. arXiv 2017, arXiv:1710.05624. [Google Scholar]
- Tellez-Limon, R.; Bahari, B.; Hsu, L.; Park, J.H.; Kodigala, A.; Kanté, B. Integrated metaphotonics: Symmetries and confined excitation of LSP resonances in a single metallic nanoparticle. Opt. Express 2016, 14, 13875–13880. [Google Scholar] [CrossRef] [PubMed]
- Espinosa-Soria, A.; Griol, A.; Martínez, A. Experimental measurement of plasmonic nanostructures embedded in silicon waveguide gaps. Opt. Express 2016, 24, 9592–9601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Downing, C.A.; Martín-Moreno, L. Polaritonic Tamm states induced by cavity photons. Nanophotonics 2021, 10, 513–521. [Google Scholar] [CrossRef]
- Yan, M. Complex-k modes of plasmonic chain waveguides. J. Phys. Commun. 2019, 3, 115015. [Google Scholar] [CrossRef] [Green Version]
- Vial, A.; Grimault, A.S.; Macías, D.; Barchiesi, D.; de la Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Wittig, T.; Schuhmann, R.; Weiland, T. Model order reduction for large systems in computational electromagnetics. Linear Algebra Its Appl. 2006, 415, 499–530. [Google Scholar] [CrossRef] [Green Version]
- He, X.J.; Wang, L.; Wang, J.M.; Tian, X.H.; Jiang, J.X.; Geng, Z.X. Electromagnetically induced transparency in planar complementary metamaterial for refractive index sensing applications. Appl. Phys. 2013, 46, 365302. [Google Scholar] [CrossRef]
- Marangos, J.P. Electromagnetically induced transparency. J. Mod. Opt. 1998, 45, 471–503. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Rayón, F.; Arroyo Carrasco, M.L.; Rodríguez-Beltrán, R.I.; Salas-Montiel, R.; Téllez-Limón, R. Plasmonic-Induced Transparencies in an Integrated Metaphotonic System. Nanomaterials 2022, 12, 1701. https://doi.org/10.3390/nano12101701
López-Rayón F, Arroyo Carrasco ML, Rodríguez-Beltrán RI, Salas-Montiel R, Téllez-Limón R. Plasmonic-Induced Transparencies in an Integrated Metaphotonic System. Nanomaterials. 2022; 12(10):1701. https://doi.org/10.3390/nano12101701
Chicago/Turabian StyleLópez-Rayón, Fernando, Maximino L. Arroyo Carrasco, René I. Rodríguez-Beltrán, Rafael Salas-Montiel, and Ricardo Téllez-Limón. 2022. "Plasmonic-Induced Transparencies in an Integrated Metaphotonic System" Nanomaterials 12, no. 10: 1701. https://doi.org/10.3390/nano12101701