Surface Effects Leading to Unusual Size Dependence of the Thermal Hysteresis Behavior in Spin-Crossover Nanoparticles
Abstract
:1. Introduction
2. Results
3. Monte Carlo Entropic Sampling
4. Results and Discussion
4.1. Size Dependence of the Equilibrium Temperature
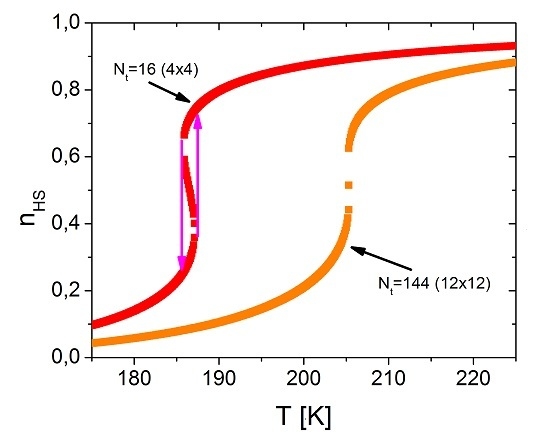
4.2. The Size Dependence of the Hysteresis Loop and the Occurrence of the First-Order Transition
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANR | Agence Nationale de la Recherche |
| BISTA-MAT | Bistabilité Magnétique |
| CNRS | Centre national de la recherche scientifique |
| GEMAC | Groupe d'Etudes de la Matière Condensée |
| LISV | Laboratoire d'Ingénierie des Systèmes de Versailles |
| MECS | Monte Carlo Entropic Sampling |
| SCO | Spin Crossover |
| UVSQ | Université de Versailles Saint Quentin en Yvelines |
References
- Gutlich, P. Spin crossover in iron(II)-complexes. Struct. Bond. 1981, 44, 83–195. [Google Scholar]
- Kahn, O.; Launay, J.P. Molecular bistability: An overview. Chemtronics 1988, 3, 140–151. [Google Scholar]
- Jeftic, J.; Hauser, A. Pressure study of the thermal spin transition and the high-spin->low-spin relaxation in the R3- and P1- crystallographic phases of [Zn1−xFex(ptz)6](BF4)2 single crystals (x = 0.1, 0.23, and 1; ptz = 1-n-propyltetrazole). J. Phys. Chem. B 1997, 101, 10262–10270. [Google Scholar] [CrossRef]
- Molnar, G.; Niel, V.; Real, J.A.; Dubrovinsky, L.; Bousseksou, A.; McGarvey, J.J. Raman spectroscopic study of pressure effects on the spin-crossover coordination polymers Fe(Pyrazine)[M(CN)4]·2H2O (M = Ni, Pd, Pt). First observation of a piezo-hysteresis loop at room temperature. J. Phys. Chem. B 2003, 107, 3149–3155. [Google Scholar] [CrossRef]
- Decurtins, S.; Gutlich, P.; Kohler, C.P.; Spiering, H.; Hauser, A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron (II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. [Google Scholar] [CrossRef]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and optical switching of iron (II) complexes. Angew. Chem. Int. Edit. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Bonhommeau, S.; Molnar, G.; Galet, A.; Zwick, A.; Real, J.A.; McGarvey, J.J.; Bousseksou, A. One shot laser pulse induced reversible spin transition in the spin-crossover complex [Fe(C4H4N2]{Pt(CN)4}] at room temperature. Angew. Chem. Int. Edit. 2005, 44, 4069–4073. [Google Scholar] [CrossRef] [PubMed]
- Moussa, N.O.; Molnar, G.; Bonhommeau, S.; Zwick, A.; Mouri, S.; Tanaka, K.; Real, J.A.; Bousseksou, A. Selective photoswitching of the binuclear spin crossover compound {[Fe(bt)(NCS)2]2(bpm)} into two distinct macroscopic phases. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Decurtins, S.; Gutlich, P.; Hasselbach, K.M.; Hauser, A.; Spiering, H. Light-induced excited-spin-state trapping in iron (II) spin-crossover systems—Optical spectroscopic and magnetic-susceptibility study. Inorg. Chem. 1985, 24, 2174–2178. [Google Scholar] [CrossRef]
- Bousseksou, A.; Boukheddaden, K.; Goiran, M.; Consejo, C.; Boillot, M.L.; Tuchagues, J.P. Dynamic response of the spin-crossover solid Co(H2(fsa)2en)(py)2 to a pulsed magnetic field. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Konig, E. Nature and dynamics of the spin-state interconversion in metal-complexes. Struct. Bond. 1991, 76, 51–152. [Google Scholar]
- Kahn, O. Spin-crossover molecular materials. Curr. Opin. Solid State Mater. Sci. 1996, 1, 547–554. [Google Scholar] [CrossRef]
- Krober, J.; Codjovi, E.; Kahn, O.; Groliere, F.; Jay, C. A spin transition system with a thermal hysteresis at room-temperature. J. Am. Chem. Soc. 1993, 115, 9810–9811. [Google Scholar] [CrossRef]
- Gallois, B.; Real, J.A.; Hauw, C.; Zarembowitch, J. Structural changes associated with the spin transition in bis(isothiocyanato)bis(1,10-phenanthroline)iron: A single-crystal x-ray investigation. Inorg. Chem. 1990, 29, 1152–1158. [Google Scholar] [CrossRef]
- Müller, E.W.; Ensling, J.; Spiering, H.; Gütlich, P. High-spin ⇌ low-spin transition in hexacoordinate complexes of iron (II) with monodentate 1-alkyltetrazole ligands: A variable-temperature moessbauer, magnetic susceptibility, and far-infrared study. Inorg. Chem. 1983, 22, 2074–2078. [Google Scholar] [CrossRef]
- Vos, G.; Le Febre, R.A.; De Graaff, R.A.G.; Haasnoot, J.G.; Reedijk, J. Unique high-spin-low-spin transition of the central ion in a linear, trinuclear iron (II) triazole compound. J. Am. Chem. Soc. 1983, 105, 1682–1683. [Google Scholar] [CrossRef]
- Konig, E.; Ritter, G.; Kulshreshtha, S.K.; Waigel, J.; Goodwin, H.A. The discontinuous high-spin (5T2)⇌low-spin (1A1) transition in solid bis(1,10-phenanthroline-2-carbaldehyde phenylhydrazone)iron(II) bis(tetrafluoroborate): Hysteresis effects, concurrent crystallographic phase change, entropy of the transition, and effect of pressure. Inorg. Chem. 1984, 23, 1896–1902. [Google Scholar]
- Konig, E.; Ritter, G.; Grunsteudel, H.; Dengler, J.; Nelson, J. Effect of a simultaneous change of temperature and pressure on the spin-state transition in bis(thiocyanato)bis(2,2'-bi-2-thiazoline)iron(II). Inorg. Chem. 1994, 33, 837–839. [Google Scholar] [CrossRef]
- Ksenofontov, V.; Spiering, H.; Schreiner, A.; Levchenko, G.; Goodwin, H.A.; Gutlich, P. The influence of hydrostatic pressure on hysteresis phase transition in spin crossover compounds. J. Phys. Chem. Solids 1999, 60, 393–399. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnar, G.; Demont, P.; Menegotto, J. Observation of a thermal hysteresis loop in the dielectric constant of spin crossover complexes: Towards molecular memory devices. J. Mater. Chem. 2003, 13, 2069–2071. [Google Scholar] [CrossRef]
- Morscheidt, W.; Jeftic, J.; Codjovi, E.; Linares, J.; Bousseksou, A.; Constant-Machado, H.; Varret, F. Optical detection of the spin transition by reflectivity: Application to [FexCo1-x(btr)2(NCS)2]·H2O. Meas. Sci. Technol. 1998, 9, 1311–1315. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: New York, NY, USA, 1993. [Google Scholar]
- Kahn, O.; Krober, J.; Jay, C. Spin transition molecular materials for displays and data recording. Adv. Mater. 1992, 4, 718–728. [Google Scholar] [CrossRef]
- Coronado, E.; Galan-Mascaros, J.R.; Monrabal-Capilla, M.; Garcia-Martinez, J.; Pardo-Ibanez, P. Bistable spin-crossover nanoparticles showing magnetic thermal hysteresis near room temperature. Adv. Mater. 2007, 19, 1359–1361. [Google Scholar] [CrossRef]
- Forestier, T.; Mornet, S.; Daro, N.; Nishihara, T.; Mouri, S.; Tanaka, K.; Fouche, O.; Freysz, E.; Letard, J.F. Nanoparticles of iron(II) spin-crossover. Chem. Commun. 2008, 4327–4329. [Google Scholar] [CrossRef] [PubMed]
- Volatron, F.; Catala, L.; Riviere, E.; Gloter, A.; Stephan, O.; Mallah, T. Spin-crossover coordination nanoparticles. Inorg. Chem. 2008, 47, 6584–6586. [Google Scholar] [CrossRef] [PubMed]
- Boldog, I.; Gaspar, A.B.; Martínez, V.; Pardo-Ibañez, P.; Ksenofontov, V.; Bhattacharjee, A.; Gütlich, P.; Real, J.A. Spin-crossover nanocrystals with magnetic, optical, and structural bistability near room temperature. Angew. Chem. 2008, 120, 6533–6537. [Google Scholar] [CrossRef]
- Forestier, T.; Kaiba, A.; Pechev, S.; Denux, D.; Guionneau, P.; Etrillard, C.; Daro, N.; Freysz, E.; Letard, J.F. Nanoparticles of [Fe(NH2-trz)3]Br2·3H2O (NH2-trz = 2-Amino-1,2,4-triazole) prepared by the reverse micelle technique: Influence of particle and coherent domain sizes on spin-crossover properties. Chem. Eur. J. 2009, 15, 6122–6130. [Google Scholar] [CrossRef] [PubMed]
- Catala, L.; Volatron, F.; Brinzei, D.; Mallah, T. Functional coordination nanoparticles. Inorg. Chem. 2009, 48, 3360–3370. [Google Scholar] [CrossRef] [PubMed]
- Galan-Mascaros, J.R.; Coronado, E.; Forment-Aliaga, A.; Monrabal-Capilla, M.; Pinilla-Cienfuegos, E.; Ceolin, M. Tuning size and thermal hysteresis in bistable spin crossover nanoparticles. Inorg. Chem. 2010, 49, 5706–5714. [Google Scholar] [CrossRef] [PubMed]
- Thibault, C.; Molnar, G.; Salmon, L.; Bousseksou, A.; Vieu, C. Soft lithographic patterning of spin crossover nanoparticles. Langmuir 2010, 26, 1557–1560. [Google Scholar] [CrossRef] [PubMed]
- Martínez, V.; Boldog, I.; Gaspar, A.B.; Ksenofontov, V.; Bhattacharjee, A.; Gütlich, P.; Real, J.A. Spin crossover phenomenon in nanocrystals and nanoparticles of [Fe(3-Fpy)2M(CN)4] (MII = Ni, Pd, Pt) two-dimensional coordination polymers. Chem. Mater. 2010, 22, 4271–4281. [Google Scholar] [CrossRef]
- Tissot, A.; Bardeau, J.-F.; Riviere, E.; Brisset, F.; Boillot, M.-L. Thermo- and photoswitchable spin-crossover nanoparticles of an iron(II) complex trapped in transparent silica thin films. Dalton Trans. 2010, 39, 7806–7812. [Google Scholar] [CrossRef] [PubMed]
- Rotaru, A.; Varret, F.; Gindulescu, A.; Linares, J.; Stancu, A.; Letard, J.; Forestier, T.; Etrillard, C. Size effect in spin-crossover systems investigated by forc measurements, for surfacted [Fe(NH2-trz)3](Br)2·3H2O nanoparticles: Reversible contributions and critical size. Eur. Phys. J. B 2011, 84, 439–449. [Google Scholar] [CrossRef]
- Jeftic, J.; Menendez, N.; Wack, A.; Codjovi, E.; Linares, J.; Goujon, A.; Hamel, G.; Klotz, S.; Syfosse, G.; Varret, F. A helium-gas-pressure apparatus with optical-reflectivity detection tested with a spin-transition solid. Meas. Sci. Technol. 1999, 10, 1059–1064. [Google Scholar] [CrossRef]
- Kawamoto, T.; Abe, S. Thermal hysteresis loop of the spin-state in nanoparticles of transition metal complexes: Monte carlo simulations on an ising-like model. Chem. Commun. 2005, 3933–3935. [Google Scholar] [CrossRef] [PubMed]
- Nicolazzi, W.; Pillet, S.; Lecomte, C. Two-variable anharmonic model for spin-crossover solids: A like-spin domains interpretation. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Konishi, Y.; Tokoro, H.; Nishino, M.; Miyashita, S. Monte carlo simulation of pressure-induced phase transitions in spin-crossover materials. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, C.; Constant-Machado, H.; Codjovi, E.; Linares, J.; Boukheddaden, K.; Varret, F. Direct access to the photo-excitation and relaxation terms in photo-switchable solids: Non-linear aspects. J. Phys. Chem. Solids 2001, 62, 1409–1422. [Google Scholar] [CrossRef]
- Wajnflasz, J.; Pick, R. Transitions ” low spin ”- ” high spin ” dans les complexes de Fe2+. J. Phys. Colloques 1971, 32, 91–92. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the 2-step spin-crossover. J. De Phys. I 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Shteto, I.; Hoo, B.; Varret, F. Dynamical model for spin-crossover solids. I. Relaxation effects in the mean-field approach. Phys. Rev. B 2000, 62, 14796–14805. [Google Scholar] [CrossRef]
- Linares, J.; Spiering, H.; Varret, F. Analytical solution of 1d ising-like systems modified by weak long range interaction - application to spin crossover compounds. Eur. Phys. J. B 1999, 10, 271–275. [Google Scholar] [CrossRef]
- Chiruta, D.; Jureschi, C.-M.; Linares, J.; Dahoo, P.; Garcia, Y.; Rotaru, A. On the origin of multi-step spin transition behaviour in 1d nanoparticles. Eur. Phys. J. B 2015, 88, 1–5. [Google Scholar] [CrossRef]
- Shteto, I.; Linares, J.; Varret, F. Monte carlo entropic sampling for the study of metastable states and relaxation paths. Phys. Rev. E 1997, 56, 5128–5137. [Google Scholar] [CrossRef]
- Linares, J.; Enachescu, C.; Boukheddaden, K.; Varret, F. Monte carlo entropic sampling applied to spin crossover solids: The squareness of the thermal hysteresis loop. Polyhedron 2003, 22, 2453–2456. [Google Scholar] [CrossRef]
- Linares, J.; Jureschi, C.-M.; Boulmaali, A.; Boukheddaden, K. Matrix and size effects on the appearance of the thermal hysteresis in 2d spin crossover nanoparticles. Phys. B Condens. Matter. 2016, 486, 164–168. [Google Scholar] [CrossRef]
- Muraoka, A.; Boukheddaden, K.; Linares, J.; Varret, F. Two-dimensional ising-like model with specific edge effects for spin-crossover nanoparticles: A monte carlo study. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]






| Description | Total | Edges | Core |
|---|---|---|---|
| Number of atoms | 4(Nx − 1) | (Nx − 2)2 | |
| Ligand-field | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linares, J.; Jureschi, C.M.; Boukheddaden, K. Surface Effects Leading to Unusual Size Dependence of the Thermal Hysteresis Behavior in Spin-Crossover Nanoparticles. Magnetochemistry 2016, 2, 24. https://doi.org/10.3390/magnetochemistry2020024
Linares J, Jureschi CM, Boukheddaden K. Surface Effects Leading to Unusual Size Dependence of the Thermal Hysteresis Behavior in Spin-Crossover Nanoparticles. Magnetochemistry. 2016; 2(2):24. https://doi.org/10.3390/magnetochemistry2020024
Chicago/Turabian StyleLinares, Jorge, Catalin Maricel Jureschi, and Kamel Boukheddaden. 2016. "Surface Effects Leading to Unusual Size Dependence of the Thermal Hysteresis Behavior in Spin-Crossover Nanoparticles" Magnetochemistry 2, no. 2: 24. https://doi.org/10.3390/magnetochemistry2020024