Through-Process Finite Element Modeling for Warm Flanging Process of Large-Diameter Aluminum Alloy Shell of Gas Insulated (Metal-Enclosed) Switchgear
Abstract
:1. Introduction
2. Description of Warm Flanging Process
3. Through-Process Finite Element Modeling for Local Heating and Integrally Flanging Whole Process
3.1. Material Parameters
3.2. Geometry Modeling and Meshing
3.3. FE Modeling of Local Heating by Flame
3.4. FE Modeling of Warm Flanging
3.5. FE Modeling of Springback
3.6. FE Modeling of Cooling
4. Results and Discussion
4.1. Forming Defects and Its Control
4.1.1. Typical Forming Defect
4.1.2. Comparison between Predicted Results and Experimental Results
4.1.3. Control of Forming Defect
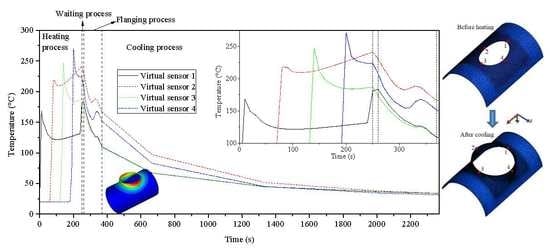
4.2. Evolution of Temperature Field for Workpiece
4.3. Deformation Characteristics of Flanging Process
4.3.1. Load and Contact
4.3.2. Evolution of Stress and Strain Fields
4.4. Analysis of Springback
5. Conclusions
- Based on FE soft FORGE code, a 3D-FE model for the heating-waiting-flanging-unloaded-cooling through-process was developed. The model was validated by comparison with geometric shapes and forming defects obtained from the experiment. The developed FE model could describe the inhomogeneous temperature field, the deformation behavior, and the springback along circumferential, radial, and axial directions of the formed branch. The finite element analysis of the warm flanging process was carried out by the developed 3D-FE model.
- Only the peripheral region of the prefabricated hole was heated, and the temperature along the radial and the circumferential directions of the elliptical prefabricated hole presented a notable inhomogeneous state. During the flanging process, the area around the minor axis (z axis) of the elliptical prefabricated hole contacted the die and deformed at first, thus the dropping degree of temperature in the region around the minor axis (z axis) was lower than that around the major axis (x axis) of the prefabricated hole. The deformed zone could maintain a suitable temperature for deformation during warm flanging.
Author Contributions
Funding
Conflicts of Interest
References
- Bojic, P. A high-speed earthing switch in gas-insulated metal enclosed switchgear. IEEE Trans. Power Deliv. 2002, 17, 117–122. [Google Scholar] [CrossRef]
- Li, C.; He, J.L.; Hu, J.; Zeng, R.; Yang, J. Switching Transient of 1000-kV UHV system considering detailed substation structure. IEEE Trans. Power Deliv. 2012, 27, 112–122. [Google Scholar] [CrossRef]
- Riechert, U.; Holaus, W. Ultra high-voltage gas-insulated switchgear—A technology milestone. Eur. Trans. Electr. Power 2012, 22, 60–82. [Google Scholar] [CrossRef]
- Wen, T.; Zhang, Q.G.; Qin, Y.F.; Zhao, J.P.; Ma, J.T.; Wu, Z.C.; Shimomura, N.; Tao, F.B.; Jia, Y.Y.; Yin, Y.; et al. On-site standard lightning impulse test for 1100-kV gas-insulated switchgear with large capactitance. IEEE Electr. Insul. Mag. 2016, 32, 36–43. [Google Scholar] [CrossRef]
- Wang, N.M.; Wenner, M.L. An analytical and experimental study of stretch flanging. Int. J. Mech. Sci. 1974, 16, 135–143. [Google Scholar] [CrossRef]
- Li, C.F.; Yang, Y.Y.; Li, S.B. Deformation analysis and die-design principles in shrink curved flanging. J. Mater. Process. Technol. 1995, 51, 164–170. [Google Scholar]
- Wang, C.T.; Kinzel, G.; Altan, T. Failure and wrinkling criteria and mathematical modeling of shrink and stretch flanging operations in sheet-metal forming. J. Mater. Process. Technol. 1995, 53, 759–780. [Google Scholar] [CrossRef]
- Hu, P.; Li, D.Y.; Li, Y.X. Analytical models of stretch and shrink flanging. Int. J. Mach. Tools Manuf. 2003, 43, 1367–1373. [Google Scholar] [CrossRef]
- Yang, H.; Fan, X.G.; Sun, Z.C.; Guo, L.G.; Zhan, M. Recent development in plastic forming technology of titanium alloys. Sci. China Technol. Sci. 2011, 54, 490–501. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.S.; Ou, H.; Long, H. Mesoscale modeling and simulation of microstructure evolution during dynamic recrystallization of a Ni-based superalloy. Appl. Phys. A 2016, 122, 890–903. [Google Scholar] [CrossRef]
- Zhang, D.W.; Li, S.P.; Jing, F.; Fan, S.Q.; Zhao, S.D. Initial position optimization of preform for large-scale strut forging. Int. J. Adv. Manuf. Technol. 2018, 94, 2803–2810. [Google Scholar] [CrossRef]
- Zhang, D.W.; Zhao, S.D.; Bi, Y.D. Analysis of forming error during thread and spline synchronous rolling process based on motion characteristic. Int. J. Adv. Manuf. Technol. 2019, 102, 915–928. [Google Scholar] [CrossRef]
- Xu, F.; Lin, Z.Q.; Li, S.H.; Xu, W.L. Study on the influences of geometrical parameters on the formability of stretch curved flanging by numerical simulation. J. Mater. Process. Technol. 2004, 145, 93–98. [Google Scholar]
- Huang, Y.M.; Chien, K.H. The formability limitation of hole-flanging process. J. Mater. Process. Technol. 2001, 117, 43–51. [Google Scholar] [CrossRef]
- Borrego, M.; Morales-Palma, D.; Martínez-Donaire, A.J.; Centeno, G.; CVallelano, C. Analysis of formability in conventional hole of AA7075-O sheets: Punch edge radius effect and limitations of the FLC. Int. J. Mater. Form. 2019. [Google Scholar] [CrossRef]
- Chen, Y.C. An analysis of forming limit in the elliptic hole-flanging process of sheet metal. J. Mater. Process. Technol. 2007, 192, 373–380. [Google Scholar] [CrossRef]
- Yu, X.Y.; Chen, J.; Chen, J.S. Influence of curvature variation on edge stretchability in hole expansion and stretch flanging of advanced high-strength steel. Int. J. Adv. Manuf. Technol. 2016, 86, 1083–1094. [Google Scholar] [CrossRef]
- Frącz, W.; Stachowicz, F.; Trzepieciński, T. Investigations of thickness distribution in hole flanging of thin steel sheets. Arch. Civ. Mech. Eng. 2012, 12, 279–283. [Google Scholar] [CrossRef]
- Vafaeesefat, A.; Khanahmadlu, M. Comparison of the numerical and experimental results of the sheet metal flange forming based on shell-elements types. Int. J. Precis. Eng. Manuf. 2011, 12, 857–863. [Google Scholar] [CrossRef]
- Kumagai, T.; Saiki, H. Deformation analysis of hole flanging with ironing of thick sheet metals. Met. Mater. 1998, 4, 711–714. [Google Scholar] [CrossRef]
- Lin, Q.Q.; Dong, W.Z.; Wang, Z.G.; Hirasawa, K. A new hole-flanging method for thick plate by upsetting by upsetting process. Trans. Nonferrous Met. Soc. China 2014, 24, 2387–2392. [Google Scholar] [CrossRef]
- Ma, Y.J.; Wang, H.W.; Hou, Y.L. Numerical simulation of GIS shell tee joint forming and its parameter optimization. Forg. Stamp. Technol. 2008, 33, 159–162. (In Chinese) [Google Scholar]
- An, H.P.; Liu, J.S. Research on new thermal hole flanging process of connection tube forming in heavy nuclear power thick-wall head. Mater. Sci. Forum 2011, 704, 119–123. [Google Scholar] [CrossRef]
- Liu, L.M.; Zhong, Z.P.; Xie, T.; Yan, H.Y. Numerical simulation and experimental study on the drawing procedure of ϕ508mm equal diameter tee. J. Plast. Eng. 2009, 16, 15–20. (In Chinese) [Google Scholar]
- Ben, N.Y.; Zhang, D.W.; Liu, N.; Zhao, X.P.; Guo, Z.J.; Zhang, Q.; Zhao, S.D. FE modeling of warm flanging process of large T-pipe from thick-wall cylinder. Int. J. Adv. Manuf. Technol. 2017, 93, 3189–3201. [Google Scholar] [CrossRef]
- Lei, C.X.; Xing, Z.W.; Xu, W.L.; Hong, Z.J.; Shan, D.B. Hot stamping of patchwork blank: Modelling and experimental investigation. Int. J. Adv. Manuf. Technol. 2017, 92, 2609–2617. [Google Scholar] [CrossRef]
- Sirvin, Q.; Velay, V.; Bonnaire, R.; Penazzi, L. Mechanical behavior modelling and finite element simulation of simple part of Ti-6Al-4V sheet under hot/warm stamping conditions. J. Manuf. Process. 2019, 38, 472–782. [Google Scholar] [CrossRef]
- Liu, H.S.; Liu, W.; Bao, J.; Xing, Z.W.; Song, B.Y.; Lei, C.X. Numerical and experimental investigation into hot forming of ultra high strength steel sheet. J. Mater. Eng. Perform. 2011, 20, 1–10. [Google Scholar] [CrossRef]
- ASM International Handbook Committee. Wrought Tool Sheets, ASM Handbook Volume 1 Properties and Section: Irons, Steels, and High Performance Alloys; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- ASM International Handbook Committee. Properties of Wrought Aluminum Alloys, ASM Handbook Volume 2 Properties and Section: Nonferrous Alloys and Special-Purpose Materials; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Zhang, D.W.; Yang, H.; Sun, Z.C. Finite element simulation of aluminum alloy cross valve forming by multi-way loading. Trans. Nonferrous Met. Soc. China 2010, 20, 1059–1066. [Google Scholar] [CrossRef]
- Zhu, D.Z.; Jia, C.X.; Yuan, Z.D.; Gong, W.M. Flame temperature measurement of the oxygen-acetylene flame spray gun. J. Eng. Thermophys. 1985, 6, 96–98. (In Chinese) [Google Scholar]
- Viskanta, R. Heat transfer to impinging isothermal gas and flame jets. Exp. Therm. Fluid Sci. 1993, 6, 103–107. [Google Scholar] [CrossRef]
- Zhang, D.W.; Yang, H.; Sun, Z.C. 3D-FE modelling and simulation of multi-way loading process for multi-ported valve. Steel Res. Int. 2010, 81, 210–215. [Google Scholar] [CrossRef]
- Takuda, H.; Mori, K.; Masuda, I.; Abe, Y.; Matsuo, M. Finite element simulation of warm deep drawing of aluminium alloy sheet when accounting for heat conduction. J. Mater. Process. Technol. 2002, 120, 412–418. [Google Scholar] [CrossRef]
- Zhang, D.W.; Ou, H.A. Relationship between friction parameters in Coulomb-Tresca friction model for bulk metal forming. Tribol. Int. 2016, 95, 13–18. [Google Scholar] [CrossRef]



























| Process | Time | |
|---|---|---|
| First stage | Local heating | t1 = 250 s |
| Second stage | Cooling | t2 = 10 s |
| Third stage | Deformation and heat transfer | t3 = 110 s |
| Fourth stage | Springback | t4 = 0 s |
| Fifth stage | Cooling | t5 = 2000 s |
| Material | AA5083 | H13 |
|---|---|---|
| Elasticity modulus E (GPa) | 73 | 210 |
| Specific heat (J⋅kg−1⋅K−1) | 1230 | 778 |
| Thermal conductivity (W⋅m−1⋅K−1) | 117 | 35.3 |
| Thermal expansion coefficient (10−6⋅K−1) | 23.75 | 10.9 |
| Emissivity | 0.05 | 0.88 |
| Process (stage) | Parameter | Value |
|---|---|---|
| Local heating (1st stage) | Temperature of heating source Tflame (°C) | 2000 |
| Heating time of heating source tflame (s) | 10 | |
| Heat transfer coefficient between billet and heat source (W⋅m−2⋅K−1) | 468,000 | |
| Heat transfer coefficient between heat source and air (W⋅m−2⋅K−1) | 40 | |
| Heating and waiting (1st and 2nd stages) | Heat transfer coefficient between billet and air (W⋅m−2⋅K−1) | 40 |
| Flanging (3rd stage) | Heat transfer coefficient between workpiece and dies (W⋅m−2⋅K−1) | 10,000 |
| Heat transfer coefficient between die and air (W⋅m−2⋅K−1) | 10 | |
| Initial temperature of dies (°C) | 20 | |
| Flanging and cooling (3rd to 5th stages) | Heat transfer coefficient between workpiece and air (W⋅m−2⋅K−1) | 10 |
| Whole process (1st to 5th stages) | Temperature of room Troom (°C) | 20 |
| Dx (mm) | Dz (mm) | Hy (mm) | ||
|---|---|---|---|---|
| Experimental results | 790 | 782 | 1088 | |
| FEM results | After flanging | 786.707 | 784.716 | 1091.181 |
| After springback | 787.434 | 784.214 | 1090.919 | |
| After cooling | 787.496 | 784.180 | 1090.657 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.-W.; Shi, T.-L.; Zhao, S.-D. Through-Process Finite Element Modeling for Warm Flanging Process of Large-Diameter Aluminum Alloy Shell of Gas Insulated (Metal-Enclosed) Switchgear. Materials 2019, 12, 1784. https://doi.org/10.3390/ma12111784
Zhang D-W, Shi T-L, Zhao S-D. Through-Process Finite Element Modeling for Warm Flanging Process of Large-Diameter Aluminum Alloy Shell of Gas Insulated (Metal-Enclosed) Switchgear. Materials. 2019; 12(11):1784. https://doi.org/10.3390/ma12111784
Chicago/Turabian StyleZhang, Da-Wei, Tian-Lin Shi, and Sheng-Dun Zhao. 2019. "Through-Process Finite Element Modeling for Warm Flanging Process of Large-Diameter Aluminum Alloy Shell of Gas Insulated (Metal-Enclosed) Switchgear" Materials 12, no. 11: 1784. https://doi.org/10.3390/ma12111784