1. Introduction
Airfoils are well known for their lift-enhancing and drag-minimizing attributes [
1,
2]. The highly streamlined shape of an airfoil is designed to prevent flow separation and the concomitant increase in the drag force. Remarkably, airfoils posses an equally exceptional thrust generating capability as well. Specifically, airfoils undergoing a prescribed rotational pitch and/or lateral oscillation have been shown to generate substantial thrust via mechanisms related to added mass and leading edge suction mechanics. Both these mechanisms have been argued to play an important role in the locomotion of natural swimmers as well [
3,
4]. In fact the body cross section of swimming fishes bears a striking resemblance with the streamlined shape of typical airfoils [
4,
5,
6]. For natural swimmers minimization of energetic cost of locomotion is of paramount importance. The morphological similarity between a streamlined foil and fish fin is therefore, a likely indicator of an energy optimality across artificial and natural locomotory-performance-maximizing thrusters. The foregoing viewpoint has been the subject of intense scrutiny over the last few decades. The viewpoint has also motivated investigations into the similarity in the wake patterns and the universality of the Strouhal number range over which natural swimmers locomote and oscillating foils produce thrust at peak propulsive efficiency [
7,
8].
For the reasons mentioned above, and also for potential deployment as high-efficiency thrusters in micro air vehicles and biomimetic autonomous underwater vehicles, it is important to quantify and optimize the thrust generation characteristics of foils undergoing prescribed oscillatory motion. The typical parametric space that must be spanned for a complete characterization of propulsive attributes and a subsequent determination of the optimal parameters is generally quite vast, even for the simplest of the prescribed kinematics. For instance pitching with a prescribed sinusoidal oscillation about a given pivot location alone leads to a three-dimensional parametric space comprised of the pitching amplitude, the Reynolds number for the incoming flow, and the Strouhal number that can be thought of as an appropriately non-dimensionalized forcing frequency. The parametric space grows rapidly once variations in the pitching waveform (multimodal non-sinusoidal waveforms) and pivot location are allowed as well. Variations in pitching waveform are important in their own right and have been shown to induce significant changes to the peak in the thrust production and the maximum achievable energetic efficiency [
9,
10,
11]. A simulation-based or experimental sweep of the enormously vast parametric is complex and overly detailed especially since the propulsive attributes are of principal interest. Reduced order models that through a simpler description of the flow facilitate a direct and rapid means of estimating the key quantities of interest (mean thrust, mean power and efficiency) are hence particularly desirable.
In this work we develop a reduced order model which by incorporating the essential features of the flow past oscillating foils, provides a significantly simpler and yet, deeply insightful description of the propulsive attributes of thrust generation from foils undergoing continuous or intermittent rotational pitch. Our model is built upon a generalization of the classical linear theory [
12,
13]. The theory was originally developed for foils undergoing small amplitude single-mode rotary oscillations in an otherwise undisturbed uniform free-stream. Our generalization extends the theory’s applicability to multimodal pitching waveforms. Since the theory relies on potential flow analysis, our model naturally incorporates the sources of thrust that are of an inviscid origin. To account for the viscous resistance arising out of the thin boundary layers that are formed over the foil’s surface, we supplement our generalized linear theory with an analysis of the viscous effects. Our analysis of viscous effects relies on the Bone-Lighthill boundary layer thinning hypothesis [
14,
15,
16] to account for the foil motion induced increase in the hydrodynamic resistance. In the large reduced frequency our model predicts a remarkable convergence to relatively simple and appealing scaling laws for the mean thrust and power coefficients. As shown in
Section 3 and
Section 4, when expressed in terms of appropriate parameters, the thrust generation characteristics of foils undergoing continuous sinusoidal and non-sinusoidal, and intermittent pitching, as reported in numerous previously published experimental and computational investigations spanning a wide range of Strouhal and Reynolds numbers, exhibit a striking convergence to simple scaling laws, in complete accordance with our model predictions.
Our present modeling approach considers thrust and drag as distinct entities with principally inviscid and purely viscous origins, respectively. Our model is thus distinct from the models that focus solely on the thrust generation aspects while completely disregarding the enhancement in viscous resistance brought about by an oscillatory foil motion [
17,
18,
19]. This enhanced viscous resistance determines the crucial transition from a drag-producing to a thrust-generating state [
20,
21]. Most importantly, the enhanced viscous resistance has been argued to be a principal determinant of the energy-optimal thrust-producing state in which an oscillating foil generates thrust at the highest propulsive efficiency [
22]. Our model accounts for both the thrust generated and the enhanced viscous resistance, and therefore our model predictions of the thrust generation characteristics include the specifics of the drag-thrust transition (or equivalently the self-propelled state) as well as the peak in the propulsive efficiency of thrust generation.
In the limit of large reduced frequency and for sufficiently large Strouhal numbers, our model predicts a Strouhal number squared dependence for the mean thrust produced from a single-mode sinusoidal pitching. Similar Strouhal number squared dependence of the mean thrust has been intuitively argued to arise from the fluid’s inertial response to the time periodic pitching motion imposed on the foil [
3,
11,
20]. Scaling laws that express the mean thrust and power coefficients in terms of the Strouhal number and reduced frequency were developed by Floryan et al. [
23]. Subsequently, simplified forms of these scaling law relations were proposed by Floryan et al. [
22]. For flapping foil motions that resemble the oscillatory gaits employed by natural swimmers. The model proposed by Floryan et al. [
22] involves free parameters. The dependence of the free parameters on the Reynolds number, the pitching amplitude and the foil thickness was analyzed by Senturk and Smits [
24].
A key distinction between the above cited previous works and our present approach lies in our rigorous treatment of the inviscid thrust generation mechanics through a generalization of the linear theory. The rigor allows for an identification of the distinct origins of thrust and crucially the reduced frequency range over which a convergence to the scaling laws including the one that relates the mean thrust to the square of the Strouhal number, is anticipated. We note here that the model for a self-propelled pitching foil proposed in the work of Moored and Quinn [
17] relied on linear theory based prediction of the thrust generated from an imposed sinusoidal pitching motion. However, pitching induced enhancement in the viscous resistance was disregarded in the analysis of Moored and Quinn [
17]. Note further that our own previous work on translationally free and constrained self-propelled foils that are pitched sinusoidally about their quarter cord makes use of linear theory to account for the distinct origins of thrust [
25]. However, the focus of this earlier work of ours was on the self-propelling state, or equivalently the drag to thrust transition. Most importantly only single-mode pitching waveforms corresponding to prescribed sinusoidal temporal variations were considered in our previous work [
25] as well as in the publications by Moored and Quinn [
17] and Fernandez-Feria and Sanmiguel-Rojas [
18]. In contrast, our present work generalizes the central idea of utilizing linear theory and Bone-Lighthill boundary layer thinning hypothesis to deduce the mean thrust, to multimodal non-sinusoidal pitching waveforms. The principal focus of our present work is on deducing generalized mean thrust and power coefficients for multimodal waveforms over a wide range of Strouhal numbers and an exhaustive comparison with the existing literature over the entire regime of drag-producing and thrust-generating pitching parameters, including the parameters that result in a self-propelled state (drag-thrust transition).
This paper is organized as follows. The configuration consisting of uniform flow past a pitching foil is described in
Section 2. Our modeling approach is described in
Section 3. This includes a detailed description of the generalized linear theory for multimodal pitching waveforms and also the complete details of the procedure adopted for theoretical estimation of thrust and viscous resistance (
Section 3.1 and
Section 3.2). An exhaustive comparison of our model predictions with a wide set of previously reported experimental and computational results on thrust generation characteristics of pitching foils is presented in
Section 4. The principal conclusions from our work are summarized in
Section 5.
2. The Configuration
The setup we analyzed consisted of a uniform flow of an incompressible fluid past a foil that is pitched about a fixed pivot location. A schematic of the setup is shown in
Figure 1. The uniform free-stream velocity is given by
, where
denotes the unit vector in the
x-direction. The foil’s cord length is denoted using
c with its time-dependent angular position indicated using
, where
t denotes the time. The pitching waveforms that are of interest are periodic and possibly non-sinusoidal. To this end, we consider a general time-periodic imposed rotational pitch such that
, where
T denotes the time period and
j is an integer. The angular location can therefore be expressed in terms of a multi-modal expansion of the form
where
, with
as the oscillation frequency and
. Here,
denotes the real part of a complex variable
z. We represent the amplitude of
by
.
The set of allowable pitching waveforms given by the Equation (
1) encompasses intermittent rotational pitch wherein a limited-duration rotary oscillation is imposed on the foil for only a fraction of the time period. Over the remaining portion of the time period, the foil is held stationary and undergoes no motion. The Reynolds number for the flow
, where
denotes the kinematic viscosity of the fluid,
and
being the density and the dynamic viscosity of the fluid, respectively. Besides Reynolds number, the Strouhal number
is an important non-dimensional parameter for characterization of the pitching foil flow configuration. Here,
A denotes the peak-to-peak excursion of the trailing edge of the foil.
3. The Model
At high Reynolds numbers, the uniform flow past a pitching foil is highly unsteady and separated. The vortical regions associated with this flow consist of the thin boundary layer regions that are formed in the immediate neighborhood of the oscillating foil’s surface, and a wake region formed downstream of the foil (see
Figure 1 for a prototypical flow at
and
for a NACA0012 foil pitched sinusoidally about the quarter chord with a). Depending on the pitching parameters, the wake region can potentially consist of either a von Karman, or a reverse von Karman, or a chaotic distribution of the shed vortices. The effect of viscosity is thus localized to the boundary layer and wake regions, elsewhere the flow is primarily inviscid. From a reduced order modeling perspective, the effective confinement of the viscous effects and principally inviscid character of the flow provides an opportunity to model the flow using inviscid models for separated flow past sharp edged bodies [
26,
27,
28,
29].
For the specific configuration of flow past a pitching foil, simple inviscid models that rely on a linearized potential flow theory based description of the unsteady flow [
12,
13,
30] are of particular interest as they lead to especially insightful closed form expressions for the key quantities of interest. The linear theory for the flow that ensues from the pitching action of the foil relies on a rather simple description in which the slender and streamlined foil is assumed to be infinitesimally thin and hence replaceable by a flat plate. In our model we assume that the thrust generated from the pitching motion of the foil is principally of an inviscid character. Our estimate of this thrust is based on the linear theory for small amplitude pitching motions. Our model for the flow therefore relies on simplifications that are similar to the ones invoked in linear theory. In essence, we model small pitching oscillations of a foil-equivalent flat plate of length
c. We define the semi-chord length
, and set the origin to coincide with the center of the foil so that the foil, or equivalently the flat plate itself extends from
to
b.
Like in the linear theory, we allow a jump in the tangential velocity component across the foil surface through a bound vortex sheet that coincides with the foil-equivalent flat plate. The bound vortex sheet therefore resides all along the flat plate
, where
s denotes the length coordinate. We enforce continuity of the normal velocity component across the flat plate forcing it to match the foil’s prescribed wall-normal motion. Additionally, like in linear theory, we employ a minimal model for the wake vorticity. Herein, we assume that the wake to be a straight line extension of the foil surface over the length coordinate
. We note here that more realistic modeling of the wake through vortex sheet topologies that mimic the high-Reynolds-number wake vorticity distribution closely is possible and has in fact been pursued in the recent work of Fernandez-Feria [
31,
32]. Our choice of a minimal wake model that is aligned perfectly with the foil-equivalent flat plate is inspired by its simplicity and its analytical tractability.
3.1. The Cycle-Averaged Thrust
Our principal interest is in the determination of the mean thrust generation characteristics of the pitching foil. The mean thrust can be directly estimated from the cycle average of the streamwise component of the normal force exerted on the foil. For small oscillations, the normal force and the lift force experienced by the foil are nearly the same. We therefore first attempt to estimate the lift force from our linear theory inspired modeling approach described in the foregoing section. To estimate the lift force, we first determine the instantaneous vortex impulse in the normal direction, i.e., in a direction perpendicular to the chordwise direction. The total vortex impulse in the chord-normal-direction can be expressed as the sum of the individual contributions from the vorticity distribution along the foil and in the wake as follows
where,
denotes the time-dependent vortex sheet strength along the foil-equivalent flat plate and in the wake. Furthermore,
, with
arising purely from the contribution of the foil motion to the bound vortex sheet and,
representing the wake contribution to the vortex sheet strength. Denoting the net circulation by
, we have
, where
denotes the quasi-steady part with
representing the wake contribution to foil circulation. Thus, we have
The lift force is related to the derivative of vorticity-impulse as follows
where the first term on the right hand side of Equation (
5) is the added-mass or reactive contribution to lift (
), the second term the quasi-steady contribution (
), and the last term arises from the explicit dependence of the lift on the wake vorticity distribution. This last term is represented by
. Thus, the total lift
. For ease of representation, we define a circulatory lift as
.
For a foil undergoing rotational pitch about a pivot location
(scaled location
), the foil’s surface velocity is given by
where a dot represents derivative with respect to time. Next, using Equations (
5) and (
6) it can be shown that
The net circulation on the foil is given by
where from the Kelvin’s circulation theorem and (4) we arrive at
Substituting (
1) in (
7), we obtain
We analyze the flow at times that are sufficiently longer than the timescale associated with the decay of the initial transients related to an impulsive start of the foil and the uniform flow. For such times, without any loss in generality, the wake vorticity assumes the form [
13]
Substituting Equations (
11) and (
12) in (
10) we obtain
Next, identifying the specific terms in the above expression (
15) with the Bessel’s functions of the first and second kind [
33] we obtain
where the reduced frequency
. Substituting Equation (
16) in (
12) and evaluating the third term on the right hand side of (
5) we deduce
Moreover,
and
where
is the Theodorsen’s function [
30]:
The net lift force exerted on the foil is therefore given by
where
is given by the expression (
11).
Having estimated the lift force exerted on the foil, we are now in a position to deduce the instantaneous thrust force exerted on the foil-equivalent flat plate. The net thrust force experienced by the foil is given by [
12],
where the leading edge suction term
S is given by
Normalizing the above expression (
24), we obtain the following for the thrust coefficient per unit span
:
We next deduce explicit expressions for each of the reactive, circulatory and suction terms that appear in the above expression. A normalization of the reactive component of the lift force given by the expression (
8) yields
From the above expression we deduce the reactive thrust coefficient as follows:
Proceeding in a similar way and normalizing the expression (
19) we obtain the following for the circulatory contribution to the lift coefficient:
so that the circulatory contribution to the thrust coefficient:
Using expression (
24) for
S we obtain the following for the leading edge suction contribution to the thrust coefficient:
The net thrust coefficient:
so that the cycle-averaged thrust coefficient
The reactive contribution to the mean thrust coefficient is given by
Similarly, the circulatory contribution to the mean thrust coefficient assumes the following form
In a similar fashion, we deduce the contribution to the mean thrust coefficient from the leading edge suction as follows
The above expressions for the mean thrust coefficient hold for generic multimodal pitching waveforms. These expressions clearly indicate that the mean thrust coefficient depends explicitly on the reduced frequency
k. Over majority of the positive-thrust-yielding parametric space the pitching is intense enough for the reduced frequency
k to far exceed unity. We therefore analyze the detailed expressions listed above in the specific limit of asymptotically large reduced frequency (
). For
, we have
while
so that the mean thrust assumes the following simplified form:
Thus, in the asymptotic limit of large reduced frequency, the mean thrust coefficient assumes a considerably simpler form. Moreover, the term can be immediately identified with the magnitude of the imposed rotational pitch . Since the magnitude of the rotational pitch is directly correlated with the magnitude of the foil’s trailing edge velocity, we next attempt to express the mean thrust coefficient in terms of the magnitude of the foil’s trailing edge speed.
For a foil undergoing periodic rotational pitch, the root mean square velocity of the trailing edge of the foil is given by
where
denotes the distance from the pivot point to the trailing edge. Thus,
and therefore
We next define a Strouhal number based on the root mean square velocity of the trailing edge as follows
Substitution of the expressions (
38) in (
39) yields
Combining the expressions (
40) and (
36) we deduce
Thus, in the limit , our generalization of the linear theory yields a remarkably simplified expression that captures the influence of variations in pitching amplitude, frequency, waveform and the pivot location on the mean thrust generated from the rotary foil oscillations.
3.2. The Viscous Resistance
Our linear theory inspired analysis of the multimodal pitching is expected to reliably predict the mean thrust generated from small amplitude rotary oscillations. However, the analysis certainly does not account for the frictional drag that originates from the boundary layers formed over the oscillating foil. As noted in several previous works, the frictional drag is quite significant and, owing to a reduction in the boundary layer thickness, rises substantially with the intensity of the pitching motion. At a self-propelled state, the viscous drag is exactly balanced by the thrust and therefore the viscous resistance is a key determinant of the self-propelled state or equivalently the drag-thrust transition point. Most importantly, the viscous drag has been argued to be a principal determinant of the optimum thrust-producing state at which a pitching foil generates thrust at the highest propulsive efficiency [
22].
For the reasons noted above, we place particular emphasis on incorporating the skin friction related hydrodynamic resistance in our overall estimation of the mean thrust. To this end, we appeal to the Bone-Lighthill boundary layer thinning hypothesis [
14] and express the cycle-averaged drag force exerted on the foil as follows [
11,
15,
16,
20]:
where
denotes the mean absolute value of the normal foil velocity [
16] with
as the drag coefficient associated with a foil held stationary in a uniform free stream that is aligned perfectly with the stationary foil’s chordwise direction. We set
in accordance with previous works [
20], where the exponent of
is quite close to the exponent of
that is anticipated from the skin friction arising out of a planar laminar boundary layer. The slight deviation from the scaling exponent of −0.5 corresponding to a planar laminar boundary layer is attributable to the geometric differences between a flat plate and a finite-thickness foil. We also note here that the exponent of
is expected to be significantly higher for a high-Reynolds-number turbulent boundary layer. Nevertheless, the exponent of −0.5 for a laminar boundary layer has been observed to represent the Reynolds number dependence of the drag coefficient over a reasonably wide range of Reynolds numbers [
20,
34].
For the specific configuration under investigation, proceeding as in our previous work [
11],
so that
from which we deduce
where
is a drag-determining parameter. We set
throughout the remainder of this paper, in accordance with our previous work on self-propelled foils that are pitched sinusoidally [
25].
Having derived an explicit form for the inviscid thrust and the viscous drag, we are now in a position to estimate the effective thrust generated from the oscillatory motion of the pitching foil. Combining the expressions (
41) and (
44) we deduce
In what follows, we make direct comparisons between the predictions from (
45) and the previously reported mean thrust coefficients deduced from experiments and detailed simulations. For notational simplicity, we denote the effective thrust using
throughout the forthcoming sections with the understanding that
is in fact
and thus fully incorporates the finite viscous resistance that arises from the laminar boundary layer formed over the pitching foil.
4. Comparisons with Experiments and Detailed Simulations
In this section we compare the thrust generation characteristics predicted from our linear theory and boundary layer thinning hypothesis inspired model for pitching foils with the previously reported experimental and computational results spanning a wide spectrum of relevant parameters. In
Figure 2 we present a comprehensive comparison of our theoretical predictions with the previously published results for a range of pitching amplitudes, Reynolds and Strouhal numbers and pitching waveforms. Our theoretical estimate (
45) suggests an effective collapse of the mean thrust coefficient with
. We therefore recast the dataset from each of the prior investigations and express them in terms of a mean thrust coefficient and the root-mean-square-Strouhal number dependence.
To begin with, we note that a re-expression of the dependence of mean thrust coefficient on pitching parameters in terms of
-
relation leads to a remarkable collapse of the discrete data set from several previous works on multimodal non-sinusoidal [
9,
10,
35] as well as single-mode sinusoidal pitching waveforms [
20,
24,
36,
37]. Specifically, we find that for a given pivot location (
a) and Reynold number
, the thrust coefficients for square-shaped, triangular-shaped and sinusoidal pitching waveforms very nearly converge to a single trend line in the
space. The convergence indicates that the
relation is relatively insensitive to the variations in pitching amplitude
, in perfect agreement with our theoretical prediction (
45). Most importantly, our key prediction that the entire influence of variations in pitching waveform on the thrust generation characteristics can be captured through a single parameter, namely the modified root-mean-square Strouhal number
, is well-supported by the past experimental and computational findings.
Our theoretical prediction (
45) is itself in reasonable quantitative agreement with the discrete data set from the prior investigations [
9,
10,
35,
36,
37]. Specifically, we find that our predictions capture the variations of
with
for a single choice of the drag-determining parameter
that is kept uniformly the same across the entire set of discrete data set and the parametric space of
,
and pitching waveform. The deviations between our theoretical predictions and the discrete data set shown in
Figure 2 are attributable to the geometric disparity between the finite-thickness foil shapes utilized in previous experimental and computational investigations (Lu et al. [
9,
35,
36] and Balla [
37] use a NACA0012 foil while Van Buren et al. [
10] employ a tear-drop shaped foil) and the foil-equivalent flat-plate assumption we made in arriving at the result (
45). We emphasize here that our theoretical analysis and the prediction (
45) are strictly valid only for small amplitude pitching motions. The slight
dependence evidenced in
Figure 2b for a tear drop shaped foil pitched about its leading edge is most likely a consequence of finite amplitude effects that are unaccounted for in our present theoretical setup.
Besides the mean thrust coefficient, the power expended in generating the mean thrust is a crucial metric that eventually determines the feasibility of utilizing pitching foils for oscillatory thrust generation in artificial systems. The mean power expended in sustaining the pitching motion of the foil is directly linked to the cycle-average of the product of the moment experienced by the foil and the angular velocity of the foil. The corresponding mean power coefficient
obtained by a normalization of the mean power with
has been shown to exhibit a cubic dependence on Strouhal number in several previous works [
8,
11,
20,
25,
36]. Given the outcome of our analysis of the mean thrust coefficient, it is then natural to expect that the pitching waveform induced variations in the power coefficient could likely be explained through a possibly simple
relationship.
To test the foregoing expectation, we reexpressed the power coefficients from the previous works of Lu et al. [
9], Van Burenin et al. [
10], Balla [
35] and Mackowski and Williamson [
36] in terms of
. The
dependence that emerges from this reexpression is depicted in
Figure 3, We find that the discrete data set from all the previous investigations [
9,
10,
35,
36,
37] converge remarkably well to a cubic scaling law of the form
. Thus, pitching waveform induced variations to the thrust generation characteristics and energetics of pitching foils are both quite well represented by
.
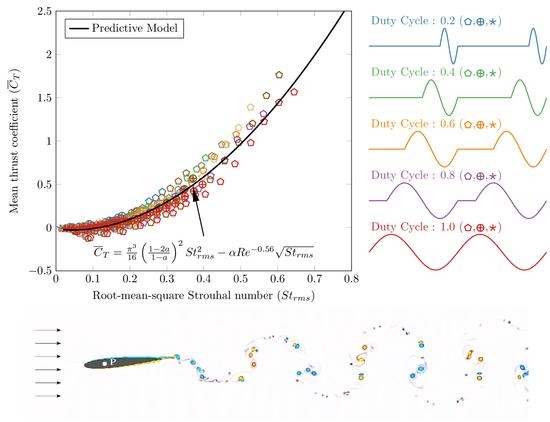
The interest in burst-and-coast mode of swimming [
38] has inspired recent investigations into the thrust generation characteristics of foils undergoing intermittent oscillations [
39,
40]. An advantage of our analysis of foils undergoing prescribed multimodal rotational pitch is that it readily applies to intermittent pitching as well. To demonstrate this, in
Figure 4 we compare our theoretical prediction (
45) and the scaling law
with the mean thrust and power coefficients for a tear drop shaped foil undergoing intermittent pitching as reported in Floryan et al. [
40]. We find that for a wide range of pitching amplitudes and duty cycles, the discrete data set from Floryan et al. [
40] is in near perfect agreement with our predictions. We may therefore conclude that the predictions from our theoretical analysis are applicable to intermittent pitching waveforms as well.
The discrete data set for the mean thrust and power coefficients associated with sinusoidal or triangle/square-shaped waveforms and intermittent pitching are thus in good agreement with our theoretical prediction (
45) and the cubic power-law scaling
. It is then reasonable to expect that the agreement will extend to the propulsive efficiency of thrust generation as well. The propulsive efficiency
is well-known to be a concave function of the Strouhal number [
8], specifically the propulsive efficiency is negative in the drag-producing regime of low Strouhal numbers and rises sharply attaining positive values for Strouhal numbers larger than a transition number of
. Precisely at the transition Strouhal number
the mean thrust vanishes identically (
) and a self-propelled state is established. For
,
increases attaining a maximum and then decreases with a further increase in
. The maximum in the propulsive efficiency
and the corresponding Strouhal number
are of particular interest as they represent optimum conditions that lead to a maximization of energetic efficiency.
The ratio of the mean thrust coefficient given by the expression (
45) and the mean power coefficient
readily yields an estimate for the propulsive efficiency
. By a maximization of this theoretical estimate with respect to
we deduce the following for the maximum propulsive efficiency:
with the corresponding Strouhal number:
In
Figure 5a we depict a comparison of the prediction (
46) from our theoretical analysis with the maximum attainable propulsive efficiency deduced from previously reported experimental and computational investigations. We observe that the
predicted from (
46) compares favorably with the maximum propulsive efficiency reported in previous works [
9,
10,
20,
24,
36,
41] over the range
. The corresponding Strouhal number
at which the maximum in propulsive efficiency is attained is compared with the previous investigations in
Figure 5b. The comparison also includes the drag-to-thrust transition Strouhal number
. We find that like
, both
and
compare favorably with the prior experimental and computational investigations over the range
.
We note here that our predictions (
46) and (
47) rely intrinsically on the Bone-Lighthill boundary layer thinning hypothesis and a laminar boundary layer assumption which we used in arriving at the expression (
44) for the cycle-averaged drag coefficient. At sufficiently large Reynolds numbers we expect a transition from a laminar to a turbulent boundary layer. The corresponding high-Reynolds-number drag coefficient
is expected to exhibit weaker dependence on
and eventually become independent of the Reynolds number. For such high Reynolds number scenarios we expect that a transition to a
-independent
will lead to a mean thrust that is independent of the Reynolds number. Consequently, at sufficiently high Reynolds number we expect a departure from the
dependence indicated by the expressions (
46) and (
47) and anticipate
,
and
to eventually become independent of the Reynolds number. This expectation is consistent with our earlier observations on a saturation in the peak propulsive efficiency of thrust generating foils that are pitched sinusoidally about their quarter chord [
20]. The expectation is also consistent with the fact that the Strouhal number range over which undulatory natural swimmers cruise at high
is particularly narrow and can essentially be viewed as being independent of the Reynolds number [
3,
6,
8,
42,
43].