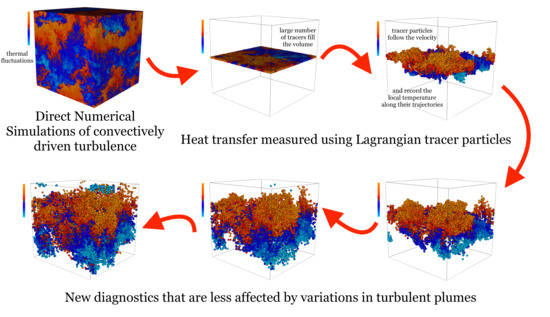
Lagrangian Statistics of Heat Transfer in Homogeneous Turbulence Driven by Boussinesq Convection
Abstract
:1. Introduction
2. Simulations
2.1. Lagrangian Tracer Particles
2.2. Rayleigh Number
3. Results: Nusselt Number
4. Results: Lagrangian Heat Structure
4.1. Definition of the Lagrangian Heat Structure
4.2. Prandtl Number Dependence of Heat Transfer in Hydrodynamic Convection
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gifford, F., Jr. Relative Atmospheric Diffusion of Smoke Puffs. J. Atmos. Sci. 1957, 14, 410–414. [Google Scholar] [CrossRef] [Green Version]
- Roberts, O. The theoretical scattering of smoke in a turbulent atmosphere. Proc. R. Soc. A-Math. Phys. 1923, 104, 640–654. [Google Scholar]
- Sutton, O.G. A theory of eddy diffusion in the atmosphere. Proc. R. Soc. A-Math. Phys. 1932, 135, 143–165. [Google Scholar]
- Frenkiel, F.; Katz, I. Studies of small-scale turbulent diffusion in the atmosphere. J. Meteorol. 1956, 13, 388–394. [Google Scholar] [CrossRef]
- Kellogg, W.W. Diffusion of smoke in the stratosphere. J. Meteorol. 1956, 13, 241–250. [Google Scholar] [CrossRef] [Green Version]
- Yeung, P. Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 2002, 34, 115–142. [Google Scholar] [CrossRef]
- Toschi, F.; Bodenschatz, E. Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 2009, 41, 375–404. [Google Scholar] [CrossRef]
- Gasteuil, Y.; Shew, W.L.; Gibert, M.; Chilla, F.; Castaing, B.; Pinton, J.F. Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh-Bénard convection. Phys. Rev. Lett. 2007, 99, 234302. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, J. Lagrangian dispersion and heat transport in convective turbulence. Phys. Rev. Lett. 2008, 100, 134502. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, J. Lagrangian studies in convective turbulence. Phys. Rev. E 2009, 79, 056301. [Google Scholar] [CrossRef]
- Emran, M.S.; Schumacher, J. Lagrangian tracer dynamics in a closed cylindrical turbulent convection cell. Phys. Rev. E 2010, 82, 016303. [Google Scholar] [CrossRef] [Green Version]
- Schütz, S.; Bodenschatz, E. Two-particle dispersion in weakly turbulent thermal convection. New J. Phys. 2016, 18, 065007. [Google Scholar] [CrossRef] [Green Version]
- Liot, O.; Seychelles, F.; Zonta, F.; Chibbaro, S.; Coudarchet, T.; Gasteuil, Y.; Pinton, J.F.; Salort, J.; Chillà, F. Simultaneous temperature and velocity Lagrangian measurements in turbulent thermal convection. J. Fluid Mech. 2016, 794, 655–675. [Google Scholar] [CrossRef] [Green Version]
- Boffetta, G.; Sokolov, I. Statistics of two-particle dispersion in two-dimensional turbulence. Phys. Fluids 2002, 14, 3224–3232. [Google Scholar] [CrossRef] [Green Version]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A 1997, 30, 1. [Google Scholar] [CrossRef] [Green Version]
- Bettencourt, J.H.; López, C.; Hernández-García, E. Characterization of coherent structures in three-dimensional turbulent flows using the finite-size Lyapunov exponent. J. Phys. A 2013, 46, 254022. [Google Scholar] [CrossRef]
- Karrasch, D.; Haller, G. Do Finite-Size Lyapunov Exponents Detect Coherent Structures? Chaos 2013, 23, 043126. [Google Scholar] [CrossRef] [Green Version]
- Salazar, J.P.; Collins, L.R. Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mech. 2009, 41, 405–432. [Google Scholar] [CrossRef] [Green Version]
- Biferale, L.; Cencini, M.; Vergni, D.; Vulpiani, A. Exit time of turbulent signals: A way to detect the intermediate dissipative range. Phys. Rev. E 1999, 60, R6295. [Google Scholar] [CrossRef] [Green Version]
- Biferale, L.; Cencini, M.; Lanotte, A.S.; Vergni, D. Inverse velocity statistics in two-dimensional turbulence. Phys. Fluids 2003, 15, 1012–1020. [Google Scholar] [CrossRef] [Green Version]
- LaCasce, J. Lagrangian statistics from oceanic and atmospheric observations. In Transport and Mixing in Geophysical Flows; Springer: Berlin/Heidelberg, Germany, 2008; pp. 165–218. [Google Scholar]
- Shew, W.L.; Gasteuil, Y.; Gibert, M.; Metz, P.; Pinton, J.F. Instrumented tracer for Lagrangian measurements in Rayleigh-Bénard convection. Rev. Sci. Instrum. 2007, 78, 065105. [Google Scholar] [CrossRef] [Green Version]
- Vassilicos, J.C. Intermittency in Turbulent Flows; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Feraco, F.; Marino, R.; Pumir, A.; Primavera, L.; Mininni, P.D.; Pouquet, A.; Rosenberg, D. Vertical drafts and mixing in stratified turbulence: Sharp transition with Froude number. EPL 2018, 123, 44002. [Google Scholar] [CrossRef] [Green Version]
- Boffetta, G.; Sokolov, I. Relative dispersion in fully developed turbulence: The Richardson?s law and intermittency corrections. Phys. Rev. Lett. 2002, 88, 094501. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Funfschilling, D.; Nobach, H.; Bodenschatz, E.; Ahlers, G. Transition to the ultimate state of turbulent Rayleigh-Bénard convection. Phys. Rev. Lett. 2012, 108, 024502. [Google Scholar] [CrossRef] [Green Version]
- Stevens, R.J.; Lohse, D.; Verzicco, R. Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 2011, 688, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Schmalzl, J.; Breuer, M.; Hansen, U. The influence of the Prandtl number on the style of vigorous thermal convection. Geophys. Astrophys. Fluid 2002, 96, 381–403. [Google Scholar] [CrossRef]
- Schumacher, J.; Götzfried, P.; Scheel, J.D. Enhanced enstrophy generation for turbulent convection in low-Prandtl-number fluids. Proc. Natl. Acad. Sci. USA 2015, 122, 9530–9535. [Google Scholar] [CrossRef] [Green Version]
- Petschel, K.; Stellmach, S.; Wilczek, M.; Lülff, J.; Hansen, U. Kinetic energy transport in Rayleigh–Bénard convection. J. Fluid Mech. 2015, 773, 395–417. [Google Scholar] [CrossRef] [Green Version]
- Williamson, J.H. Low-storage Runge-Kutta schemes. J. Comput. Phys. 1980, 35, 48–56. [Google Scholar] [CrossRef]
- Calzavarini, E.; Lohse, D.; Toschi, F.; Tripiccione, R. Rayleigh and Prandtl number scaling in the bulk of Rayleigh-Bénard turbulence. Phys. Fluids 2005, 17, 055107. [Google Scholar] [CrossRef] [Green Version]
- Pratt, J.; Busse, A.; Müller, W.C. Fluctuation dynamo amplified by intermittent shear bursts in convectively driven magnetohydrodynamic turbulence. Astron. Astrophys. 2013, 557, A76. [Google Scholar] [CrossRef]
- Pratt, J.; Busse, A.; Mueller, W.C.; Chapman, S.; Watkins, N. Anomalous dispersion of Lagrangian particles in local regions of turbulent flows revealed by convex hull analysis. arXiv 2014, arXiv:1408.5706. [Google Scholar]
- Pratt, J.; Busse, A.; Müller, W.; Watkins, N.; Chapman, S.C. Extreme-value statistics from Lagrangian convex hull analysis for homogeneous turbulent Boussinesq convection and MHD convection. New J. Phys. 2017, 19, 065006. [Google Scholar] [CrossRef] [Green Version]
- Gibert, M.; Pabiou, H.; Chilla, F.; Castaing, B. High-Rayleigh-number convection in a vertical channel. Phys. Rev. Lett. 2006, 96, 084501. [Google Scholar] [CrossRef] [Green Version]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Grötzbach, G. Spatial resolution requirements for direct numerical simulation of the Rayleigh-Bénard convection. J. Comput. Phys. 1983, 49, 241–264. [Google Scholar] [CrossRef]
- Kaczorowski, M.; Wagner, C. Study on the resolution requirements for DNS in turbulent Rayleigh-Bénard convection. In Turbulence and Interactions; Springer: Berlin/Heidelberg, Germany, 2010; pp. 199–205. [Google Scholar]
- Homann, H.; Dreher, J.; Grauer, R. Impact of the floating-point precision and interpolation scheme on the results of DNS of turbulence by pseudo-spectral codes. Comput. Phys. Commun. 2007, 177, 560–565. [Google Scholar] [CrossRef] [Green Version]
- Busse, A.; Müller, W.C. Diffusion and dispersion in magnetohydrodynamic turbulence: The influence of mean magnetic fields. Astron. Nachrichten Astron. Notes 2008, 329, 714–716. [Google Scholar] [CrossRef]
- Buaria, D.; Pumir, A.; Feraco, F.; Marino, R.; Pouquet, A.; Rosenberg, D.; Primavera, L. Single-particle Lagrangian statistics from direct numerical simulations of rotating-stratified turbulence. Phys. Rev. Fluids 2020, 5, 064801. [Google Scholar] [CrossRef]
- Niemela, J. Static and dynamic measurements of the Nusselt number in turbulent convection. Phys. Scr. 2013, 2013, 014059. [Google Scholar] [CrossRef]
- Stevens, R.J.; Verzicco, R.; Lohse, D. Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 2010, 643, 495–507. [Google Scholar] [CrossRef] [Green Version]
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 27–56. [Google Scholar] [CrossRef] [Green Version]
- Chillà, F.; Schumacher, J. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E Soft Matter 2012, 35, 1–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef] [Green Version]
- Rempel, E.L.; Chian, A.L.; Brandenburg, A. Lagrangian coherent structures in nonlinear dynamos. Astrophys. J. Lett. 2011, 735, L9. [Google Scholar] [CrossRef]
- Rempel, E.L.; Chian, A.C.; Brandenburg, A. Lagrangian chaos in an ABC-forced nonlinear dynamo. Phys. Scr. 2012, 86, 018405. [Google Scholar] [CrossRef] [Green Version]
- Rempel, E.L.; Chian, A.C.L.; Brandenburg, A.; Muñoz, P.R.; Shadden, S.C. Coherent structures and the saturation of a nonlinear dynamo. J. Fluid Mech. 2013, 729, 309–329. [Google Scholar] [CrossRef] [Green Version]
- Dubbeldam, D.; Ford, D.C.; Ellis, D.E.; Snurr, R.Q. A new perspective on the order-n algorithm for computing correlation functions. Mol. Simul. 2009, 35, 1084–1097. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions, 9th ed.; U.S. Government Printing Office: Washington, DC, USA, 1970.
- Emran, M.; Schumacher, J. Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 2008, 611, 13–34. [Google Scholar] [CrossRef] [Green Version]












| Simulation | HC1 | HC2 | HC3 | HC4 |
|---|---|---|---|---|
| grid size | ||||
| simulation time () | 484 | 1605 | 416 | 427 |
| () | 4 | 4 | 4 | 8 |
| Prandtl number | 0.1 | 1.0 | 10 | 1.0 |
| Rayleigh number | ||||
| Grashof number | ||||
| Reynolds number | 3230 | 1350 | 570 | 4180 |
| Nusselt no. | 582 | 2025 | 6980 | 6503 |
| time maximum of | 651 | 3200 | 8873 | 7903 |
| () | 3.43 | 7.60 | 17.0 | 3.23 |
| () | 1.85 | 5.03 | 4.57 | 1.64 |
| () | 1.92 | 7.57 | 3.01 | 3.24 |
| () | 10.18 | 2.21 | 2.52 | 2.86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pratt, J.; Busse, A.; Müller, W.-C. Lagrangian Statistics of Heat Transfer in Homogeneous Turbulence Driven by Boussinesq Convection. Fluids 2020, 5, 127. https://doi.org/10.3390/fluids5030127
Pratt J, Busse A, Müller W-C. Lagrangian Statistics of Heat Transfer in Homogeneous Turbulence Driven by Boussinesq Convection. Fluids. 2020; 5(3):127. https://doi.org/10.3390/fluids5030127
Chicago/Turabian StylePratt, Jane, Angela Busse, and Wolf-Christian Müller. 2020. "Lagrangian Statistics of Heat Transfer in Homogeneous Turbulence Driven by Boussinesq Convection" Fluids 5, no. 3: 127. https://doi.org/10.3390/fluids5030127