Defect Process, Dopant Behaviour and Li Ion Mobility in the Li2MnO3 Cathode Material
Abstract
:1. Introduction
2. Computational Methods
3. Results
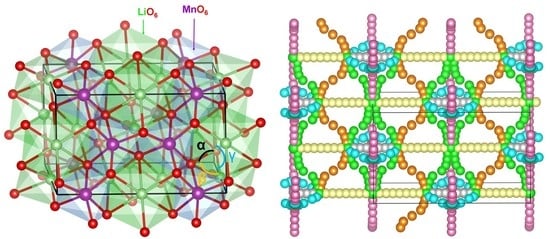
3.1. Bulk Li2MnO3 Structure
3.2. Intrinsic Defect Processes
3.3. Lithium Ion Diffusion
3.4. Trivalent Doping
3.5. Tetravalent Doping
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652. [Google Scholar] [CrossRef] [PubMed]
- Whittingham, M.S. Lithium batteries and cathode materials. Chem. Rev. 2004, 104, 4271–4302. [Google Scholar] [CrossRef] [PubMed]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Nytén, A.; Abouimrane, A.; Armand, M.; Gustafsson, T.; Thomas, J.O. Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material. Electrochem. Commun. 2005, 7, 156–160. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Hayase, S.; Kanno, R.; Yashima, M.; Nakayama, N.; Yamada, A. Structure of Li2FeSiO4. J. Am. Chem. Soc. 2008, 130, 13212–13213. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and lithium transport pathways in li2fesio4 cathodes for lithium batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef]
- Masquelier, C.; Croguennec, L. Polyanionic (phosphates, silicates, sulfates) frameworks as electrode materials for rechargeable Li (or Na) batteries. Chem. Rev. 2013, 113, 6552–6591. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; Liu, Z.; Li, H.; Liu, Y.; Wang, Z.; Li, X.; Shih, K.; Mai, L. Li3V(MoO4)3 as a novel electrode material with good lithium storage properties and improved initial coulombic efficiency. Nano Energy 2018, 44, 272–278. [Google Scholar] [CrossRef]
- Recham, N.; Chotard, J.N.; Dupont, L.; Delacourt, C.; Walker, W.; Armand, M.; Tarascon, J.M. A 3.6 V lithium-based fluorosulphate insertion positive electrode for lithium-ion batteries. Nat. Mater. 2009, 9, 68. [Google Scholar] [CrossRef] [PubMed]
- Afyon, S.; Wörle, M.; Nesper, R. A lithium-rich compound Li7Mn(BO3)3 containing Mn2+ in tetrahedral coordination: A cathode candidate for lithium-ion batteries. Angew. Chemie Inter. Ed. 2013, 52, 12541–12544. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, S.-I.; Nakamura, M.; Natsui, R.; Yamada, A. New lithium iron pyrophosphate as 3.5 V class cathode material for lithium ion battery. J. Am. Chem. Soc. 2010, 132, 13596–13597. [Google Scholar] [CrossRef] [PubMed]
- Thackeray, M.M.; Johnson, C.S.; Vaughey, J.T.; Li, N.; Hackney, S.A. Advances in manganese-oxide ‘composite’ electrodes for lithium-ion batteries. J. Mater. Chem. 2005, 15, 2257–2267. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Rana, J.; Stan, M.; Kloepsch, R.; Li, J.; Schumacher, G.; Welter, E.; Zizak, I.; Banhart, J.; Winter, M. Structural changes in Li2MnO3 cathode material for Li-ion batteries. Adv. Energy Mater. 2014, 4, 1300998. [Google Scholar] [CrossRef]
- Francis Amalraj, S.; Markovsky, B.; Sharon, D.; Talianker, M.; Zinigrad, E.; Persky, R.; Haik, O.; Grinblat, J.; Lampert, J.; Schulz-Dobrick, M.; et al. Study of the electrochemical behavior of the “inactive” Li2MnO3. Electrochim. Acta 2012, 78, 32–39. [Google Scholar] [CrossRef]
- Ammundsen, B.; Paulsen, J. Novel lithium-ion cathode materials based on layered manganese oxides. Adv. Mater. 2001, 13, 943–956. [Google Scholar] [CrossRef]
- Robertson, A.D.; Bruce, P.G. The origin of electrochemical activity in Li2MnO3. Chem. Commun. 2002, 2790–2791. [Google Scholar] [CrossRef]
- Chen, H.; Islam, M.S. Lithium extraction mechanism in Li-Rich Li2MnO3 involving oxygen hole formation and dimerization. Chem. Mater. 2016, 28, 6656–6663. [Google Scholar] [CrossRef]
- Cho, E.; Kim, K.; Jung, C.; Seo, S.-W.; Min, K.; Lee, H.S.; Park, G.-S.; Shin, J. Overview of the oxygen behavior in the degradation of Li2MnO3 cathode material. J. Phys. Chem. C 2017, 121, 21118–21127. [Google Scholar] [CrossRef]
- Xiang, Y.; Wu, X. Enhanced electrochemical performances of Li2MnO3 cathode materials by Al doping. Ionics 2018, 24, 83–89. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 lithium battery material: Atomic-scale study of defects, lithium mobility, and trivalent dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Kuganathan, N.; Islam, M.S. Defect chemistry and lithium-ion migration in polymorphs of the cathode material Li2MnSiO4. J. Mater. Chem. A 2013, 1, 4207–4214. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kordatos, A.; Kuganathan, N.; Kelaidis, N.; Iyngaran, P.; Chroneos, A. Defects and lithium migration in Li2CuO2. Sci. Rep. 2018, 8, 6754. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Chroneos, A. Defects, dopants and sodium mobility in Na2MnSiO4. Sci. Rep. 2018, 8, 14669. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects and dopant properties of Li3V2(PO4)3. Sci. Rep. 2019, 9, 333. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, dopants and lithium mobility in Li9V3(P2O7)3 (PO4)2. Sci. Rep. 2018, 8, 8140. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Iyngaran, P.; Chroneos, A. Lithium diffusion in Li5FeO4. Sci. Rep. 2018, 8, 5832. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Li2SnO3 as a cathode material for lithium-ion batteries: Defects, lithium ion diffusion and dopants. Sci. Rep. 2018, 8, 12621. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect chemistry and Li-ion diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Kelaidis, N.; Chroneos, A. Defects, lithium mobility and tetravalent dopants in the Li3NbO4 cathode material. Sci. Rep. 2019, 9, 2192. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Kordatos, A.; Fitzpatrick, M.E.; Vovk, R.V.; Chroneos, A. Defect process and lithium diffusion in Li2TiO3. Solid State Ionics 2018, 327, 93–98. [Google Scholar] [CrossRef]
- Kuganathan, N.; Tsoukalas, L.H.; Chroneos, A. Defects, dopants and Li-ion diffusion in Li2SiO3. Solid State Ionics 2019, 335, 61–66. [Google Scholar] [CrossRef]
- Araújo, C.M.; Blomqvist, A.; Scheicher, R.H.; Chen, P.; Ahuja, R. Superionicity in the hydrogen storage material Li2NH: Molecular dynamics simulations. Phys. Rev. B 2009, 79, 172101. [Google Scholar] [CrossRef]
- Seymour, I.D.; Chroneos, A.; Kilner, J.A.; Grimes, R.W. Defect processes in orthorhombic LnBaCo2O5.5 double perovskites. Phys. Chem. Chem. Phys. 2011, 13, 15305–15310. [Google Scholar] [CrossRef] [PubMed]
- Jay, E.E.; Rushton, M.J.D.; Chroneos, A.; Grimes, R.W.; Kilner, J.A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 2015, 17, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D.; Rohl, A.L. The general utility lattice program (GULP). Molec. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef] [Green Version]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Varotsos, P. Defect volumes and the equation of state in α-PbF2. Phys. Rev. B 2007, 76, 092106. [Google Scholar] [CrossRef]
- Varotsos, P. Comparison of models that interconnect point defect parameters in solids with bulk properties. J. Appl. Phys. 2007, 101, 123503. [Google Scholar] [CrossRef]
- Chroneos, A.; Vovk, R.V. Modeling self-diffusion in UO2 and ThO2 by connecting point defect parameters with bulk properties. Solid State Ionics 2015, 274, 1–3. [Google Scholar] [CrossRef]
- Chroneos, A. Connecting point defect parameters with bulk properties to describe diffusion in solids. Appl. Phys. Rev. 2016, 3, 041304. [Google Scholar] [CrossRef]
- Strobel, P.; Lambert-Andron, B. Crystallographic and magnetic structure of Li2MnO3. J. Solid State Chem. 1988, 75, 90–98. [Google Scholar] [CrossRef]
- Boulineau, A.; Croguennec, L.; Delmas, C.; Weill, F. Reinvestigation of Li2MnO3 structure: Electron diffraction and high resolution TEM. Chem. Mater. 2009, 21, 4216–4222. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the concentrations of imperfections in crystalline solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Ensling, D.; Stjerndahl, M.; Nytén, A.; Gustafsson, T.; Thomas, J.O. A comparative XPS surface study of Li2FeSiO4/C cycled with LiTFSI- and LiPF6-based electrolytes. J. Mater. Chem. 2009, 19, 82–88. [Google Scholar] [CrossRef]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of antisite defects on li diffusion in LiFePO4 revealed by Li isotope exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ionics 2019, 336, 75–79. [Google Scholar] [CrossRef]
- Kuganathan, N.; Iyngaran, P.; Vovk, R.; Chroneos, A. Defects, dopants and Mg diffusion in MgTiO3. Sci. Rep. 2019, 9, 4394. [Google Scholar] [CrossRef] [PubMed]
- Hoang, K. Doping Li-rich cathode material Li2MnO3: Interplay between lattice site preference, electronic structure, and delithiation mechanism. Phys. Rev. Mater. 2017, 1, 075404. [Google Scholar] [CrossRef]
- Kong, F.; Longo, R.C.; Park, M.-S.; Yoon, J.; Yeon, D.-H.; Park, J.-H.; Wang, W.-H.; Kc, S.; Doo, S.-G.; Cho, K. Ab initio study of doping effects on LiMnO2 and Li2MnO3 cathode materials for Li-ion batteries. J. Mater. Chem. A 2015, 3, 8489–8500. [Google Scholar] [CrossRef]








| Parameter | Calculated | Experiment [44] | |∆|(%) |
|---|---|---|---|
| a (Å) | 4.8715 | 4.9370 | 1.33 |
| b (Å) | 8.3519 | 8.5320 | 2.11 |
| c (Å) | 5.0177 | 5.0300 | 0.24 |
| α (°) | 90.0 | 90.0 | 0.00 |
| β (°) | 110.07 | 109.46 | 0.56 |
| γ (°) | 90.0 | 90.0 | 0.00 |
| Migration Path | Li–Li Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 2.65 | 0.27 |
| B | 2.77 | 0.37 |
| C | 2.83 | 0.44 |
| D | 2.84 | 0.45 |
| E | 2.85 | 0.59 |
| F | 2.87 | 0.47 |
| Long-Range Path | Direction | Overall Activation Energy (eV) |
|---|---|---|
| A→E→E→A | b axis | 0.59 |
| F→B→B→ B | ab plane | 0.47 |
| C→C→C→C | ac plane | 0.44 |
| D→D→D→D | bc plane | 0.45 |
| F→F→F→F | ab plane | 0.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N.; Sgourou, E.N.; Panayiotatos, Y.; Chroneos, A. Defect Process, Dopant Behaviour and Li Ion Mobility in the Li2MnO3 Cathode Material. Energies 2019, 12, 1329. https://doi.org/10.3390/en12071329
Kuganathan N, Sgourou EN, Panayiotatos Y, Chroneos A. Defect Process, Dopant Behaviour and Li Ion Mobility in the Li2MnO3 Cathode Material. Energies. 2019; 12(7):1329. https://doi.org/10.3390/en12071329
Chicago/Turabian StyleKuganathan, Navaratnarajah, Efstratia N. Sgourou, Yerassimos Panayiotatos, and Alexander Chroneos. 2019. "Defect Process, Dopant Behaviour and Li Ion Mobility in the Li2MnO3 Cathode Material" Energies 12, no. 7: 1329. https://doi.org/10.3390/en12071329