Simulation of Polymer Crystallization under Isothermal and Temperature Gradient Conditions Using Particle Level Set Method
Abstract
:1. Introduction
2. Particle Level Set for Polycrystals Growth
2.1. Level Set Method
2.2. Particle Level Set Method
- (i)
- Particle initialization. When the initial surface is defined, the particles need to be placed within three cells of the interface. Each particle stores its position and radius, which is used to perform error correction on the level set function. The radius is set so that the boundary is just touching the interface:where and is the sign of the particle, set to +1 if and −1 if In [14], they recommend that 16 particles be placed in each cell in 2D.
- (ii)
- Particle update: The positions of the particles are updated using a second order Runga Kutta (RK2) time integration:Error correction: Whenever a particle escapes the interface by more than its radius, it will be used to perform error correction on the interface. To enable error correction, a local level set value for each corner of the escaped particle is defined as follows:Error correction is performed using the positive particles to create a temporary grid and the negative particles to a temporary grid For all of the escaped positive particles, the values on cell corners containing the escaped particles are calculated by Equation (12), the value for each corner is then set toSimilarly, for all the escaped negative particles, the value for each corner is set toThen, for each grid node, the minimum absolute value is chosen as the final correction for
- (iii)
- Particle reseeding: With the interface stretching and tearing, regions that lack a sufficient number of particles in the computational domain will form. Reseeding is carried out to delete the particles that are superfluous or far away from the interface and distribute a new set of particles to ensure that there is a uniform distribution of particles near the interface. It is important to note that if the simulation does not cause the particles to be unevenly distributed, there is no reason to reseed.
2.3. Particle Level Set Method for Polycrystals Growth
3. Morphological Model for Isothermal Crystallization of Polymer
3.1. Nucleation
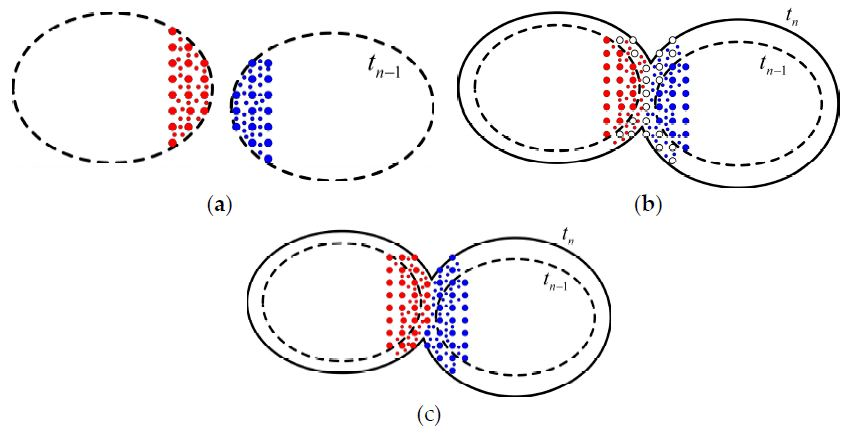
3.2. Growth and Impingement
3.3. Algorithm for Polymer Crystallization under Isothermal Conditions
4. Morphological Model for Polymer Crystallization in a Temperature Gradient
5. Results and Discussion
5.1. Problem Formulation
5.2. Isothermal Case
5.2.1. Morphological Development
5.2.2. Overall Crystallization Kinetics
5.3. Temperature Gradient Case
5.3.1. Effects of Temperature Gradient
5.3.2. Morphological Development
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, H.M. Computer Modeling for Injection Molding: Simulation, Optimization, and Control; John Wiley & Son: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zheng, R.; Tanner, R.; Fan, X.J. Injection Molding: Integration of Theory and Modeling Methods; Springer: Berlin, Germany, 2011. [Google Scholar]
- Spina, R.; Spekowius, M.; Hopmann, C. Multiphysics simulation of thermoplastic polymer crystallization. Mater. Des. 2016, 95, 455–469. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Dahlmann, R.; Hopmann, C. Analysis of polymer crystallization and residual stresses in injection molded parts. Int. J. Precis. Eng. Manuf. 2014, 15, 89–96. [Google Scholar] [CrossRef]
- Roozemond, P.C.; van Erp, T.B.; Peters, G.W.M. Flow-induced crystallization of isotactic polypropylene: Modeling formation of multiple crystal phases and morphologies. Polymer 2016, 89, 69–80. [Google Scholar] [CrossRef]
- Xu, K.L.; Guo, B.H.; Reiter, R.; Xu, J. Simulation of secondary nucleation of polymer crystallization via a model of microscopic kinetics. Chin. Chem. Lett. 2015, 26, 1105–1108. [Google Scholar] [CrossRef]
- Swaminarayan, S.; Charbon, C. A multiscale model for polymer crystallization. I: Growth of individual spherulites. Polym. Eng. Sci. 1998, 38, 634–643. [Google Scholar] [CrossRef]
- Charbon, C.; Swaminarayan, S. A multiscale model for polymer crystallization. II: Solidification of a macroscopic part. Polym. Eng. Sci. 1998, 38, 644–656. [Google Scholar] [CrossRef]
- Raabe, D.; Godara, A. Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton. Model. Simul. Mater. Sci. Eng. 2005, 13, 733–751. [Google Scholar] [CrossRef]
- Xu, H.; Bellehumeur, C.T. Modeling the morphology development of ethylene copolymers in rotational molding. J. Appl. Polym. Sci. 2006, 102, 5903–5917. [Google Scholar] [CrossRef]
- Xu, H.; Bellehumeur, C.T. Morphology development for single-site ethylene copolymers in rotational molding. J. Appl. Polym. Sci. 2008, 107, 236–245. [Google Scholar] [CrossRef]
- Ruan, C.; Ouyang, J.; Liu, S. Multi-scale modeling and simulation of crystallization during cooling in short fiber reinforced composites. Int. J. Heat Mass Transf. 2012, 55, 1911–1921. [Google Scholar] [CrossRef]
- Liu, Z.J.; Ouyang, J.; Zhou, W.; Wang, X.D. Numerical simulation of the polymer crystallization during cooling stage by using level set method. Comput. Mater. Sci. 2015, 97, 245–253. [Google Scholar] [CrossRef]
- Enright, D.; Fedkiw, R.; Ferziger, J.; Mitchell, I. A hybrid particle level set method for improved interface capturing. J. Comput. Phys. 2002, 183, 83–116. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R. Level Set Methods and Dynamics Implicit Surfaces; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sussman, M.; Fatemi, E.; Smereka, P.; Osher, S. An improved level set method for incompressible two-phase flows. Comput. Fluids 1998, 27, 663–680. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Bourlioux, A. A coupled level-set volume-of-fluid algorithm for tracking material interfaces. In Proceedings of the 6th International Symposium on Computational Fluid Dynamics, Lake Tahoe, CA, USA, 4–8 September 1995.
- Enright, D.; Losasso, F.; Fedkiw, R. A fast and accurate semi-Lagrangian particle level set method. Comput. Struct. 2005, 83, 479–490. [Google Scholar] [CrossRef]
- Zalesak, S.T. Fully multidimensional flux-corrected transport algorithms for fluids. J. Comput. Phys. 1979, 31, 335–362. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision and Materials Science; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Piorkowska, E. Modeling of polymer crystallization in a temperature gradient. J. Appl. Polym. Sci. 2002, 86, 1351–1362. [Google Scholar] [CrossRef]
- Lauritzen, S.I.; Hoffman, J.D. Theory of formation of polymer crystals with folded chains in dilute solution. J. Res. Natl. Bur. Stand. 1960, 64A, 73–102. [Google Scholar] [CrossRef]
- Tan, L.J. Multiscale Modeling of Solidification of Multi-Component Alloys. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2007. [Google Scholar]
- Adalsteinsson, D.; Sethian, J.A. The fast construction of extension velocities in level set methods. J. Comput. Phys. 1999, 148, 2–22. [Google Scholar] [CrossRef]
- Anantawaraskul, S.; Ketdee, S.; Supaphol, P. Stochastic simulation for morphological development during the isothermal crystallization of semicrystalline polymers: A case study of syndiotactic polypropylene. J. Appl. Polym. Sci. 2009, 111, 2260–2268. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar]
- Avrami, M. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Piorkowska, E.; Gregory, C.R. Handbook of Polymer Crystallization; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Pawlak, A.; Piorkowska, E. Crystallization of isotactic polypropylene in a temperature gradient. Colloid Polym. Sci. 2001, 279, 939–946. [Google Scholar] [CrossRef]















| Parameter | Physical Meaning | Value |
|---|---|---|
| (cal·mol−1) | Activation energy of motion | 1500 |
| (cm·s−1) | Parameter in Hoffman–Lauritzen expression for the laminar growth rate | |
| (°C) | A temperature typically 30 K below the glass transition | −41.95 |
| (K2) | Parameter in Hoffman–Lauritzen expression for the growth rate | |
| (°C) | Melting temperature | 185.05 |
| (J (K·mol)−1) | Gas constant | 8.314472 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Ouyang, J.; Ruan, C.; Liu, Q. Simulation of Polymer Crystallization under Isothermal and Temperature Gradient Conditions Using Particle Level Set Method. Crystals 2016, 6, 90. https://doi.org/10.3390/cryst6080090
Liu Z, Ouyang J, Ruan C, Liu Q. Simulation of Polymer Crystallization under Isothermal and Temperature Gradient Conditions Using Particle Level Set Method. Crystals. 2016; 6(8):90. https://doi.org/10.3390/cryst6080090
Chicago/Turabian StyleLiu, Zhijun, Jie Ouyang, Chunlei Ruan, and Qingsheng Liu. 2016. "Simulation of Polymer Crystallization under Isothermal and Temperature Gradient Conditions Using Particle Level Set Method" Crystals 6, no. 8: 90. https://doi.org/10.3390/cryst6080090