Broadband Active Control of Transverse Scattering from All-Dielectric Nanoparticle
Abstract
:1. Introduction
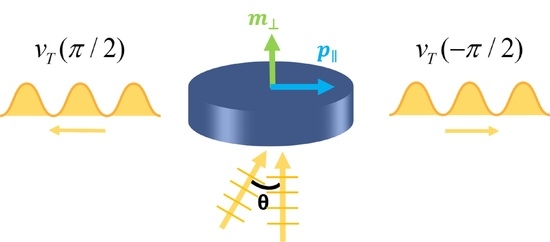
2. Principle of Coherent Control for Transverse Scattering
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, Z.; Sun, F.; Huang, W.; Jiang, J.; Zhan, R.; Ke, Y.; Chen, H.; Deng, S. Phonon Polaritons in Twisted Double-Layers of Hyperbolic van der Waals Crystals. Nano Lett. 2020, 20, 5301–5308. [Google Scholar] [CrossRef]
- Liu, W.; Kivshar, Y.S. Generalized Kerker effects in nanophotonics and meta-optics. Opt. Express 2018, 26, 13085–13105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geffrin, J.-M.; Garcia, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L.S.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; et al. Magnetic and electric coherence in forward- and back-scattered electromagnetic waves by a single dielectric subwavelength sphere. Nat. Commun. 2012, 3, 1171. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.H.; Kuznetsov, A.; Miroshnichenko, A.; Yu, Y.F.; Luk’Yanchuk, B. Directional visible light scattering by silicon nanoparticles. Nat. Commun. 2013, 4, 1527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gómez-Medina, R.; García-Cámara, B.; Suárez-Lacalle, I.; Gonzalez, F.; Moreno, F.; Nieto-Vesperinas, M.; Sáenz, J.J. Electric and magnetic dipolar response of germanium nanospheres: Interference effects, scattering anisotropy, and optical forces. J. Nanophotonics 2011, 5, 053512. [Google Scholar] [CrossRef] [Green Version]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’Yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef] [Green Version]
- García-Etxarri, A.; Gómez-Medina, R.; Froufe-Pérez, L.S.; Lopez, C.; Chantada, L.; Scheffold, F.; Aizpurua, J.; Vesperinas, M.N.; Sáenz, J.J. Strong magnetic response of submicron Silicon particles in the infrared. Opt. Express 2011, 19, 4815–4826. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’Yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Decker, M.; Staude, I.; Falkner, M.; Dominguez, J.; Neshev, D.N.; Brener, I.; Pertsch, T.; Kivshar, Y.S. High-efficiency dielectric Huygens’ surfaces. Adv. Opt. Mater. 2015, 3, 813–820. [Google Scholar] [CrossRef] [Green Version]
- Bag, A.; Neugebauer, M.; Woźniak, P.; Leuchs, G.; Banzer, P. Transverse Kerker Scattering for Angstrom Localization of Nanoparticles. Phys. Rev. Lett. 2018, 121, 193902. [Google Scholar] [CrossRef] [Green Version]
- Shamkhi, H.K.; Baryshnikova, K.V.; Sayanskiy, A.; Kapitanova, P.; Terekhov, P.; Belov, P.; Karabchevsky, A.; Evlyukhin, A.B.; Kivshar, Y.; Shalin, A.S. Transverse Scattering and Generalized Kerker Effects in All-Dielectric Mie-Resonant Metaoptics. Phys. Rev. Lett. 2019, 122, 193905. [Google Scholar] [CrossRef] [Green Version]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Zheludev, N.I. Obtaining optical properties on demand. Science 2015, 348, 973–974. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y.; Huang, L.; Xu, L.; Miroshnichenko, A.E.; Lee, R.-K. Broadband control on scattering events with interferometric coherent waves. New J. Phys. 2021, 23, 063014. [Google Scholar] [CrossRef]
- Lee, J.Y.; Chung, Y.-H.; Miroshnichenko, A.E.; Lee, R.-K. Linear control of light scattering with multiple coherent waves excitation. Opt. Lett. 2019, 44, 5310–5313. [Google Scholar] [CrossRef]
- Xi, Z.; Wei, L.; Adam, A.J.L.; Urbach, H.P. Broadband active tuning of unidirectional scattering from nanoantenna using combined radially and azimuthally polarized beams. Opt. Lett. 2015, 41, 33–36. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; MacDonald, K.; Zheludev, N. Controlling light-with-light without nonlinearity. Light. Sci. Appl. 2012, 1, e18. [Google Scholar] [CrossRef] [Green Version]
- Roger, T.; Vezzoli, S.; Bolduc, E.; Valente, J.; Heitz, J.J.F.; Jeffers, J.; Soci, C.; Leach, J.; Couteau, C.; Zheludev, N.I.; et al. Coherent perfect absorption in deeply subwavelength films in the single-photon regime. Nat. Commun. 2015, 6, 7031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, J.; Fang, X.; Rogers, E.; Plum, E.; MacDonald, K.; Zheludev, N. Coherent control of Snell’s law at metasurfaces. Opt. Express 2014, 22, 21051–21060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neugebauer, M.; Woźniak, P.; Bag, A.; Leuchs, G.; Banzer, P. Polarization-controlled directional scattering for nanoscopic position sensing. Nat. Commun. 2016, 7, 11286. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Zayats, A.V.; Rodríguez-Fortuño, F.J. Interferometric Evanescent Wave Excitation of a Nanoantenna for Ultrasensitive Displacement and Phase Metrology. Phys. Rev. Lett. 2018, 121, 193901. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Ng, T.F.J.; Lin, Z.; Chan, C.T. Optical pulling force. Nat. Photon. 2011, 5, 531–534. [Google Scholar] [CrossRef] [Green Version]
- Pu, M.; Feng, Q.; Wang, M.; Hu, C.; Huang, C.; Ma, X.; Zhao, Z.; Wang, C.; Luo, X. Ultrathin broadband nearly perfect absorber with symmetrical coherent illumination. Opt. Express 2012, 20, 2246–2254. [Google Scholar] [CrossRef] [PubMed]
- Karabchevsky, A.; Katiyi, A.; Ang, A.; Hazan, A. On-chip nanophotonics and future challenges. Nanophotonics 2020, 9, 3733–3753. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015, 7, 66–106. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Ong, H. Momentum-dependent group velocity of surface plasmon polaritons in two-dimensional metallic nanohole array. Opt. Express 2016, 24, 12489–12500. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.; Miroshnichenko, A.; Brongersma, M.L.; Kivshar, Y.S.; Luk’Yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, 2472. [Google Scholar] [CrossRef] [Green Version]
- Evlyukhin, A.B.; Reinhardt, C.; Chichkov, B.N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Phys. Rev. B 2011, 84, 235429. [Google Scholar] [CrossRef]
- Hinamoto, T.; Fujii, M. MENP: An open-source MATLAB implementation of multipole expansion for nanophotonics. OSA Contin. 2021, 4, 1640–1648. [Google Scholar] [CrossRef]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. Exact Multipolar Decompositions with Applications in Nanophotonics. Adv. Opt. Mater. 2018, 7, 1800783. [Google Scholar] [CrossRef] [Green Version]
- Van De Groep, J.; Polman, A. Designing dielectric resonators on substrates: Combining magnetic and electric resonances. Opt. Express 2013, 21, 26285–26302. [Google Scholar] [CrossRef]
- Staude, I.; Miroshnichenko, A.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I.; et al. Tailoring Directional Scattering through Magnetic and Electric Resonances in Subwavelength Silicon Nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef] [PubMed]
- Long, S.; McAllister, M.; Shen, L. The resonant cylindrical dielectric cavity antenna. IRE Trans. Antennas Propag. 1983, 31, 406–412. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Zhu, H.; Li, J.; Cao, Z.; Chen, H. Broadband Active Control of Transverse Scattering from All-Dielectric Nanoparticle. Crystals 2021, 11, 920. https://doi.org/10.3390/cryst11080920
Yu H, Zhu H, Li J, Cao Z, Chen H. Broadband Active Control of Transverse Scattering from All-Dielectric Nanoparticle. Crystals. 2021; 11(8):920. https://doi.org/10.3390/cryst11080920
Chicago/Turabian StyleYu, Huiwen, Hongjia Zhu, Jinyang Li, Zhaolong Cao, and Huanjun Chen. 2021. "Broadband Active Control of Transverse Scattering from All-Dielectric Nanoparticle" Crystals 11, no. 8: 920. https://doi.org/10.3390/cryst11080920