Optimization Algorithms of Neural Networks for Traditional Time-Domain Equalizer in Optical Communications
Abstract
:1. Introduction
2. Optimization Problems of Equalizers with Traditional Structures
3. Optimization Algorithms for Equalizers with Traditional Structures
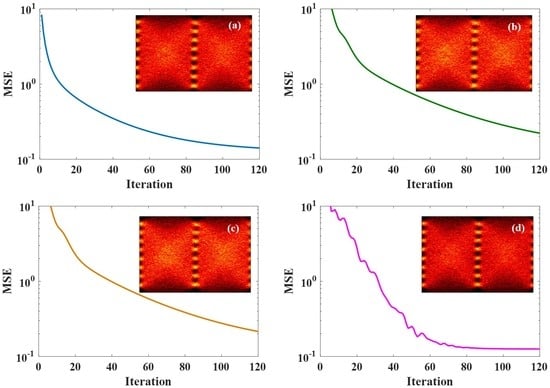
3.1. BGD Method
3.2. AdaGrad
3.3. RMSProp
3.4. Adam
4. Experimental Setups
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial neural network nonlinear equalizer for coherent optical OFDM. IEEE Photonics Technol. Lett. 2014, 27, 387–390. [Google Scholar] [CrossRef]
- Ahmad, S.T.; Kumar, K.P. Radial basis function neural network nonlinear equalizer for 16-QAM coherent optical OFDM. IEEE Photonics Technol. Lett. 2016, 28, 2507–2510. [Google Scholar] [CrossRef]
- Ye, C.; Zhang, D.; Huang, X.; Feng, H.; Zhang, K. Demonstration of 50Gbps IM/DD PAM4 PON over 10GHz class optics using neural network based nonlinear equalization. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar]
- Gaiarin, S.; Pang, X.; Ozolins, O.; Jones, R.T.; Da Silva, E.P.; Schatz, R.; Westergren, U.; Popov, S.; Jacobsen, G.; Zibar, D. High speed PAM-8 optical interconnects with digital equalization based on neural network. In Proceedings of the 2016 Asia Communications and Photonics Conference (ACP), Wuhan, China, 2–5 November 2016; pp. 1–3. [Google Scholar]
- Gou, P.; Yu, J. A nonlinear ANN equalizer with mini-batch gradient descent in 40Gbaud PAM-8 IM/DD system. Opt. Fiber Technol. 2018, 46, 113–117. [Google Scholar] [CrossRef]
- Rajbhandari, S.; Ghassemlooy, Z.; Angelova, M. Effective denoising and adaptive equalization of indoor optical wireless channel with artificial light using the discrete wavelet transform and artificial neural network. J. Light. Technol. 2009, 27, 4493–4500. [Google Scholar] [CrossRef]
- Haigh, P.A.; Ghassemlooy, Z.; Rajbhandari, S.; Papakonstantinou, I.; Popoola, W. Visible light communications: 170 Mb/s using an artificial neural network equalizer in a low bandwidth white light configuration. J. Light. Technol. 2014, 32, 1807–1813. [Google Scholar] [CrossRef]
- Khan, F.N.; Zhou, Y.; Lau, A.P.T.; Lu, C. Modulation format identification in heterogeneous fiber-optic networks using artificial neural networks. Opt. Express 2012, 20, 12422–12431. [Google Scholar] [CrossRef] [Green Version]
- Sorokina, M.; Sergeyev, S.; Turitsyn, S. Fiber echo state network analogue for high-bandwidth dual-quadrature signal processing. Opt. Express 2019, 27, 2387–2395. [Google Scholar] [CrossRef]
- An, S.; Zhu, Q.; Li, J.; Ling, Y.; Su, Y. 112-Gb/s SSB 16-QAM signal transmission over 120-km SMF with direct detection using a MIMO-ANN nonlinear equalizer. Opt. Express 2019, 27, 12794–12805. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Bülow, H.; Leven, A. Applying neural networks in optical communication systems: Possible pitfalls. IEEE Photonics Technol. Lett. 2017, 29, 2091–2094. [Google Scholar] [CrossRef]
- Bottou, L.; Bousquet, O. The tradeoffs of large scale learning. In Proceedings of the Neural Information Processing Systems Conference, Vancouver, BC, Canada, 3–8 December 2007; pp. 161–168. [Google Scholar]
- Domingos, P.M. A few useful things to know about machine learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef] [Green Version]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Battiti, R. First-and second-order methods for learning: between steepest descent and Newton’s method. Neural Comput. 1992, 4, 141–166. [Google Scholar] [CrossRef]
- Xiong, X.; De la Torre, F. Supervised descent method and its applications to face alignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 532–539. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Nielsen, T.; Chandrasekhar, S. OFC 2004 workshop on optical and electronic mitigation of impairments. J. Light. Technol. 2005, 23, 131–142. [Google Scholar]
- Watts, P.M.; Mikhailov, V.; Savory, S.; Bayvel, P.; Glick, M.; Lobel, M.; Christensen, B.; Kirkpatrick, P.; Shang, S.; Killey, R.I. Performance of single-mode fiber links using electronic feed-forward and decision feedback equalizers. IEEE Photonics Technol. Lett. 2005, 17, 2206–2208. [Google Scholar] [CrossRef]
- Haykin, S.S. Adaptive Filter Theory; Pearson Education India: Noida, India, 2005. [Google Scholar]
- Wang, H.; Zhou, J.; Li, F.; Liu, L.; Yu, C.; Yi, X.; Huang, X.; Liu, W.; Li, Z. Variable-step DD-FTN algorithm for PAM8-based short-reach optical interconnects. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 5–10 May 2019. paper SW4O. [Google Scholar]
- Zhou, J.; Qiao, Y.; Huang, X.; Yu, C.; Cheng, Q.; Tang, X.; Guo, M.; Liu, W.; Li, Z. Joint FDE and MLSD Algorithm for 56-Gbit/s Optical FTN-PAM4 System Using 10G-Class Optics. J. Light. Technol. 2019, 37, 3343–3350. [Google Scholar] [CrossRef]
- Li, J.; Tipsuwannakul, E.; Eriksson, T.; Karlsson, M.; Andrekson, P.A. Approaching Nyquist limit in WDM systems by low-complexity receiver-side duobinary shaping. J. Light. Technol. 2012, 30, 1664–1676. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital signal processing for short-reach optical communications: A review of current technologies and future trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: London, UK, 2016. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]





| BGD | AdaGrad | RMSProp | Adam | |
|---|---|---|---|---|
| Add. | ||||
| Mul. | ||||
| Sqrt. | 0 | N | N | N |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhou, J.; Wang, Y.; Wei, J.; Liu, W.; Yu, C.; Li, Z. Optimization Algorithms of Neural Networks for Traditional Time-Domain Equalizer in Optical Communications. Appl. Sci. 2019, 9, 3907. https://doi.org/10.3390/app9183907
Wang H, Zhou J, Wang Y, Wei J, Liu W, Yu C, Li Z. Optimization Algorithms of Neural Networks for Traditional Time-Domain Equalizer in Optical Communications. Applied Sciences. 2019; 9(18):3907. https://doi.org/10.3390/app9183907
Chicago/Turabian StyleWang, Haide, Ji Zhou, Yizhao Wang, Jinlong Wei, Weiping Liu, Changyuan Yu, and Zhaohui Li. 2019. "Optimization Algorithms of Neural Networks for Traditional Time-Domain Equalizer in Optical Communications" Applied Sciences 9, no. 18: 3907. https://doi.org/10.3390/app9183907