Topological rainbow trapping based on gradual valley photonic crystals

1 Introduction

In recent years, topological photonic crystals (PCs) have attracted much attention due to their practicability in robust waveguides [1–3], robust delay lines [4], high-Q cavities [5], and high-performance lasers [6]. A valley, the energy extreme of a band structure, has been widely studied in two-dimensional electric materials [7, 8] and it is introduced into the sonic [9–13] and photonic [14–26] realms. The Dirac points of topological valley PCs will open when the inversion symmetry is broken, and there are deterministic edge states within the non-trivial band gap. For valley PCs with a triangular or honeycomb lattice, bulk bands show valley characteristics around K and K′ points (the two non-equivalent Brillouin-zone corners). Due to the time-reversal symmetry, the Berry curvature satisfies F(k) = -F(-k), and the Chern number is zero [1]. However, the difference between the two valleys’ Chern numbers, defined as $∆C=C_K-C_{K^{\prime }}$, is quantized [27]. The PCs with opposite non-zero ΔC can be formed into supercells to generate topological edge states.

Rainbow trapping, which means different frequency components of a guided wave stop at different spatial positions, has been realized in traditional systems [28, 29]. Various schemes are proposed to realize topological rainbows, such as the gradient of the structural parameters in a photonic system [30], gradient rotation angle in an acoustic system [13], and height gradient in an elastic wave system [31]. The combination of topology with a rainbow [13, 30–38] has increased the possibility of designing topologically protected devices, such as buffering, routing, and wave-matter interaction enhancement devices. The topological photonic rainbow provides a full dais to realize the success of potential applications akin to integrated photonic devices and high-speed information processing chips [39].

Non-Hermitian systems have been actively studied recently [40–45]. Loss or gain has been used to investigate non-Hermitian systems is an all-purpose technique in photonics. In real cases, generality of materials suffers from loss, which is a challenge in practical applications. It is worth studying to explore the effect of loss on the devices.

Structures based on rotated gradient valley PCs in the square lattice are designed in this study to realize the topological rainbow trapping. Different rotated angles correspond to different topological edge modes, which ensures the realization of topological rainbow trapping. The effect of introducing losses on topological rainbows is discussed in this study. For a structure with gradient angles, the same or different loss can be applied to every pillar in a cell. The topological protection against loss is demonstrated. For structures with only one rotation angle, the loss gradient can achieve topological rainbow trapping. These results show that the topological rainbow trapping can also be realized in non-Hermitian systems. Moreover, the rainbow trapping pattern in the Hermitian and non-Hermitian systems is not significantly affected by the introduction of defects or disorders, which further indicates the robustness of the topological protection.

2 Topological rainbow trapping

2.1 The valley PC

The two-dimensional (2D) valley PCs with square lattices used are shown in Figure 1A. Eight circular dielectric pillars of silicon with n = 3.48 are embedded in an air background ($n=1$), which is taken as a unit cell to compose the square lattice. n is the refractive index. In Figure 1A, the lattice constant a is 420 nm. The diameter d of pillars is 40 nm. The length of the side of a square formed by pillars is labeled by b, which is 200 nm. The band structure diagram with a transverse magnetic (TM) mode is shown in Figure 1B. The Brillouin zone (BZ) is shown in the inset. The high symmetry line is Γ-X-M-Γ. The purple lines show the fourth and fifth bands of the unit cell in Figure 1A. Two Dirac points are localized at D₁ and D₂, labeled by red points. When the inversion symmetry of the unit cell is broken by pillars rotating around the cell center by θ, the Dirac points split, and a non-trivial gap is generated. The clockwise rotation (anticlockwise rotation) is defined as θ > 0° (θ < 0°). When θ = ±15°, the band diagram is shown as blue lines in Figure 1B, and the cyan region indicates the band gap. The pillar shape in the cell can be random, like all right triangles or rectangles. In addition, it is also possible to have pillars with different shapes in one cell. If the area of the pillars, the constant a, and b remain the same, their band structure diagram remains unchanged compared with Figure 1B.

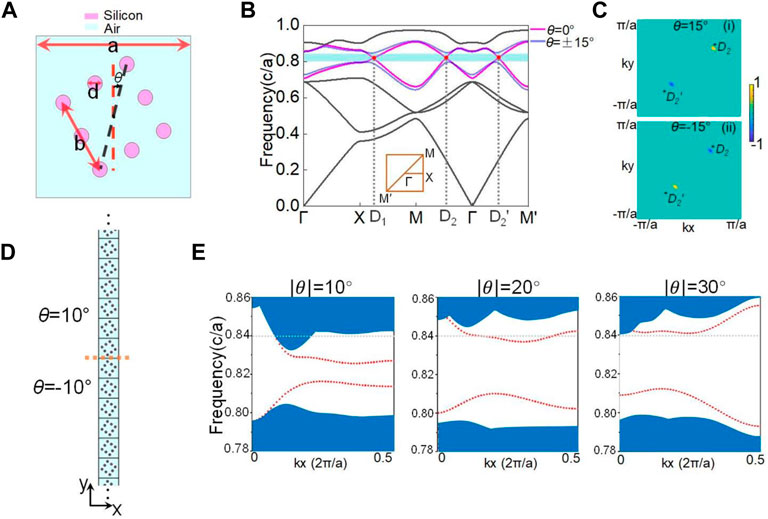
FIGURE 1. (A) Unit cell schematic representation with θ = 15°. Purple represents silicon, and cyan represents air. (B) Band structure diagram. The dark lines are the bands common to cells with θ = 0° and ±15°. When θ = 0°, the purple lines show the fourth and fifth bands, and degenerate points are marked with red. When θ = ±15°, the blue lines show the fourth and fifth bands, and the cyan region is the corresponding band gap. The first BZ with high symmetry points is shown in the inset. (C) Berry curvature distribution on BZ of the fourth band when θ = 15° and θ = −15°. (D) Supercell schematic representation. θ above and below the orange dashed line is 10° and −10°, respectively. (E) Three pictures are the projected band structure of supercells with $\left|\theta \right|$ = 10°, 20°, and 30°. The blue region represents the bulk band, and the red dotted line represents the edge states. The gray dotted line denotes the frequency of 0.840c/a.

After degeneracy points split D₂ and $D_2^{\prime }$ two highly symmetric positions in the momentum space, came the valley. The two valleys have the same band morphology but different topological characteristics. The topological invariant, the valley Chern number, is calculated. The Berry curvature is defined as follows:

It is integrated to give the valley Chern number C_V. $A_{\mu }\left(\mathit{k}\right)$ is the Berry connection defined as follows:

where $\left|n\left(\mathit{k}\right)\right.〉$ represents the nth normalized eigenstates using the Bloch wave vector k. Berry curvature distributions on the BZ of the fourth band of unit cells with θ = ±15° are calculated numerically here. The finite element method (FEM) is used to calculate normalized eigenstates, in this case, the electric field. The BZ is discretized to many cells, and the Berry curvature is calculated on each cell. The numerical calculation process can be shown as follows:

Based on these formulas, the Berry curvature at many ${\mathit{k}}_l$ points is calculated, resulting in Figure 1C. As shown in this diagram, the extreme value locations of the Berry curvature are near the band valleys at D₂ and $D_2^{\prime }$. The opposite rotated directions correspond to the opposite Berry curvature distributions. For the unit cell with θ = 15°, the valley Chern number of D₂ ($C_{D_2}$) is equal to 1, and $C_{D_2^{\prime }}$ is equal to −1. On the contrary, the values of the unit cell with θ = −15° are the opposite. $∆C=C_{D_2}-C_{D_2^{\prime }}$ is defined in this square lattice. Therefore, $∆C$ of the unit cell with θ = 15° is 2, and the unit cell with θ = −15° is −2, which exhibits these two cells’ different topological characteristics.

2.2 Rainbow trapping in the valley PC

Topological edge states can be formed between structures with different topological invariants. The supercell is constructed as shown in Figure 1D, of which the orange dashed line has 10 cells on each side. Unit cells above and below the orange dashed line rotate in opposite directions. When $\left|\theta \right|$ are 10°, 20°, and 30°, the projected band structures of supercells are exhibited in Figure 1E. There are two edge state lines in each relationship diagram, marked in red. The upper edge dispersion states are studied in this paper. When the angles increase, the dispersion curves of edge modes move to a higher frequency region. Therefore, the forbidden frequency of each edge mode can be trapped in the graded structure by stacking the supercells by continually increasing the angle in the propagation direction. For example, the light with a frequency of 0.840c/a is in the bulk state for rotating 10°, at the edge mode for rotating 20°, and at the band gap for rotating 30°. The change of the dispersion relationship as the angle increases makes it possible to realize the topological rainbow. In Figure 2A, the group velocity of the upper edge state is calculated as a function of frequency. The zero-group velocity points are at the conversion of positive and negative group velocities, labeled by dark dashed circles. As the angle increases, the frequency, where the group velocity is zero, increases. Although there are also zero-group velocity positions at frequencies between 0.845c/a and 0.860c/a, the corresponding edge states extend to the bulk, making them meaningless. The edge states in the gap and zero-group velocity are the keys to realizing the topological rainbow.

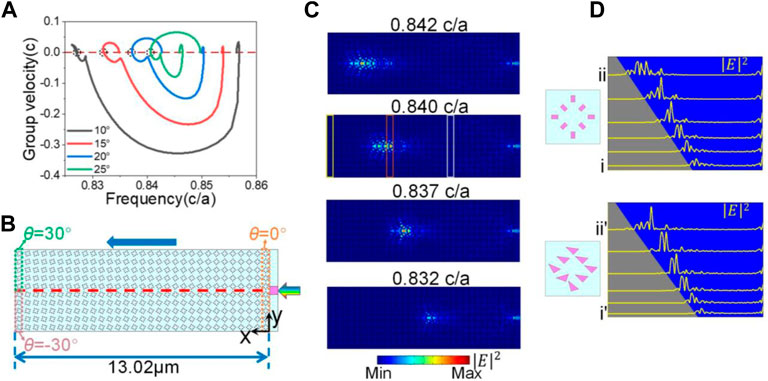
FIGURE 2. (A) Group velocity of upper edge states of supercells with different rotated angles. The red dashed line is where the group velocity is zero. Black dashed circles indicate the zero-group velocity positions. (B) Configuration used to implement the topological rainbow. The rotated angle of the supercell increases the degree one by one from the right to the left. Light is incident from the right through a waveguide. (C) ${\left|\mathit{E}\right|}^{\mathbf{2}}$ field distribution of different frequencies. (D) Unit cells with other shaped pillars are used to realize a topological rainbow. The corresponding ${\left|\mathit{E}\right|}^{\mathbf{2}}$ distribution along the red dashed line of (B) is shown on the left side of the cells. The yellow lines at different positions represent different frequencies. i represents a frequency of 0.801c/a, and ii represents 0.811c/a. i' is 0.712c/a, and ii’ is 0.722c/a. The blue and gray parts show the regions of existence and non-existence of the edge states.

A gradient structure design is conceived to achieve rainbow trapping, as shown in Figure 2B. From right to left, $\left|\theta \right|$ are increased from 0° to 30°. The red dashed line denotes the middle line of this structure. Every pillar above and below the red dashed line has the same rotation angles but in opposite directions. When light is incident from right through a waveguide, waves with different frequencies are localized at different positions, as shown in Figure 2C. In the second diagram, the energy with a frequency of 0.840c/a, diffused at the position with 10° (the white wireframe), is localized at the position around 20° (the orange wireframe) and is forbidden by the position with 30° (the yellow wireframe). This phenomenon is consistent with the dispersion relationships and the group velocity diagram. We also calculate the energy distribution for other pillar-shaped structures. We give the ${\left|E\right|}^2$ distributions on the middle line of the gradient structure for two-unit cells, as shown in Figure 2D. The results are shown on the right of the corresponding unit cell. The blue and gray parts exhibit the regions of existence and non-existence of the edge modes. Photonic states with different frequencies are localized at different positions. Because of the different pillar areas of these unit cells, the frequency range of the rainbow is different. According to the results, the internal pillar shape does not affect the rainbow-trapping realization, which shows our design’s university.

2.3 Rainbow trapping in the non-Hermitian valley PC

For the non-Hermitian case, we introduce loss in the valley PC to explore the topological rainbow trapping, so the material’s refractive index has an imaginary part. The pillars’ refractive index is set to $n=3.48+i\times n_l\left(n_l>0\right)$. $n_l$ stands for the loss of the material. The eigenfrequency solver is used for this calculation by using the FEM.

As shown in Figure 3A, for the structure with $\left|\theta \right|$ increasing from 0° to 30°, a certain loss is applied to each pillar. There are two cases considered. In the first case, the same loss $n_l=0.5$ is applied to each pillar in a unit cell. In the second case, different losses ($n_l=0.2\sim 0.9$) are applied on each pillar. Pillars with different losses are denoted with different colors. The ${\left|E\right|}^2$ distribution profiles are shown below the unit cells correspondingly. The introduction of the same or different losses in a unit cell does not destroy the realization of the topological rainbow, which shows a good application prospect.

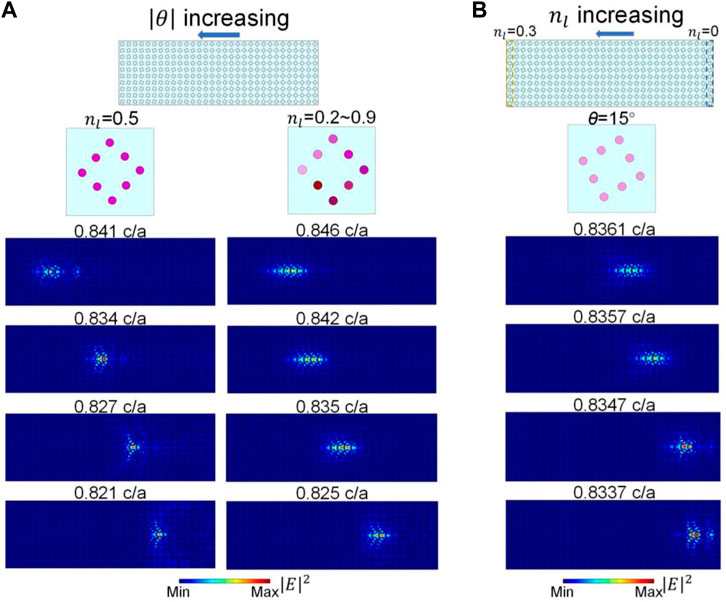
FIGURE 3. (A) Angle of the structure is gradually increasing ($\left|\theta \right|$ = 0°∼30°). A certain loss is applied on each pillar of a cell. Two cases are calculated. The same loss ($n_l$ = 0.5) and different losses ($n_l$ = 0.2∼0.9) are applied to each pillar in a cell separately. The ${\left|\mathit{E}\right|}^{\mathbf{2}}$ distribution profiles are shown below the unit cells, correspondingly. (B) Angle of the structure is certain ($\left|\theta \right|$ = 15°). The gradient loss ($n_l$ = 0∼0.3) applied on the structure is used to achieve topological rainbow trapping. The ${\left|\mathit{E}\right|}^{\mathbf{2}}$ distribution profiles are shown below the unit cells.

The loss can affect the frequencies of the edge modes, which can also lead to the rainbow trapping. As shown in Figure 3B, $\left|\theta \right|$ is fixed, which equals 15°. Loss applied on each pillar in one cell is the same. For the whole structure, $n_l$ gradually increases from 0 to 0.3 from the right to the left. The ${\left|E\right|}^2$ distribution profiles are shown below the unit cell. We can see that different frequencies of light are localized at different locations. The topological rainbow based on losses is realized. Most materials in the real world have intrinsic losses. The topological protection against loss is demonstrated, which means the topological rainbow trapping can also be realized in non-Hermitian systems. This property helps the structure to be more easily used in practical applications.

2.4 Verification of robustness

In order to further investigate the robustness of the topological rainbow, defects and disorders are introduced into this configuration, whose position is chosen randomly. The detailed defects and disorders are framed in the boxes of Figure 4. The black dashed graphics are the original appearance of the pillars. For the valley PC, three cases are given. The pillar’s shapes and disturbances differ between the three cases. In Figure 4A, the pillars’ shape is a circle, and several are missing. In Figure 4B, the pillars come in three shapes, and two are dislocated from the original centers. The parameters of the displacement are $a*\left(\pm \frac{1}{42},\pm \frac{1}{42}\right)$, respectively. In Figure 4C, all the shapes of the pillars are equilateral triangles, and two pillars’ area is enlarged to 6/5 of their original size. The ${\left|E\right|}^2$ field distributions are shown below the corresponding structures, showing that these disturbances do not destroy the rainbow trapping.

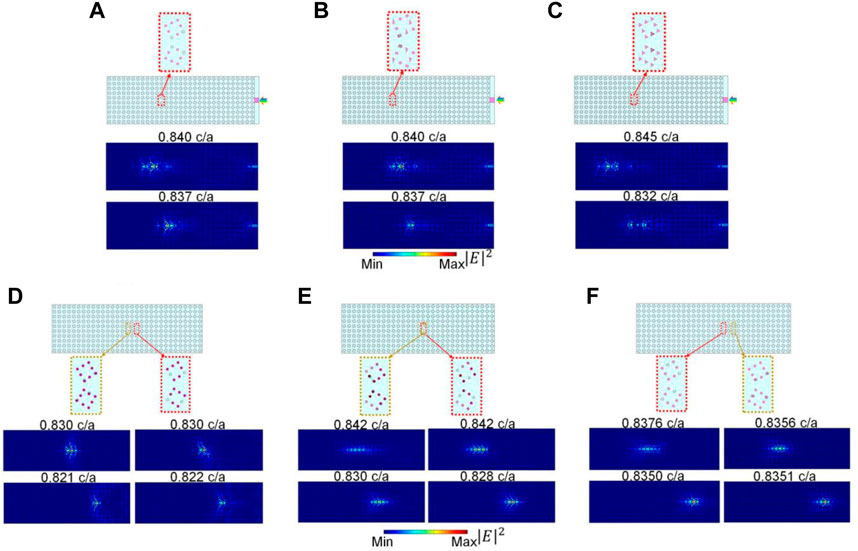
FIGURE 4. Defects and disorders are introduced in the structures, as shown in the dotted boxes. The black dashed graphics are the original appearance of pillars. (A–C) are the three cases of the Hermitian system. The pillar’s shapes and disturbances are both different between them. (D–F) are the non-Hermitian cases, which are the results of introducing defects and disorders into the structure mentioned in Section 2.3. Defects are framed in red, and disorders are framed in ginger. The corresponding ${\left|\mathit{E}\right|}^{\mathbf{2}}$ field distribution diagrams are shown below the detailed structures.

For the non-Hermitian valley PC, defects and disorders are introduced into each of the three constructs mentioned in Section 2.3, as shown in Figures 4D–F. Defects and disorders are framed in red and ginger on the structure separately. Defects are realized by two pillars missing from each of the two cells. The corresponding ${\left|E\right|}^2$ field distributions are shown below the red boxes. The pillars are moved $a*\left(\pm \frac{1}{42},\pm \frac{1}{42}\right)$ from their original position to introduce disorders. The field distributions are shown below the detailed disorders, and the rainbow trapping is yet to be realized.

Defects and disorders are placed in the middle of the structure, i.e., in the unit cells near the light transmission path, but these do not prevent light trapping. To sum up, the results shown in Figure 4 demonstrate the design’s robustness and topological protection. The ability of anti-interference both in Hermitian and non-Hermitian systems makes our design a good application prospect.

3 Conclusion

In conclusion, topological rainbow trapping based on gradient valley PC is proposed in this study. Lights with different frequencies are spread, separated, and finally trapped at different positions from the gradient structure. For Hermitian valley PC, topological rainbow trapping can be realized for the arbitrary pillars’ shape, which provides flexibility in practical applications. For non-Hermitian valley PC, the same or different loss applied in a unit cell does not influence the rainbow trapping. Moreover, for a loss gradient structure, rainbow trapping can be realized. For Hermitian and non-Hermitian systems, the robustness of the formed topological rainbow trapping is further demonstrated by introducing defects and disorders.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CL supervised the project and guided the work. XW performed the calculations and wrote the manuscript. WZ, SE, and CL revised the manuscript. All authors participated in discussions and contributed to this work.

Acknowledgments

CL acknowledges the support from the National Natural Science Foundation of China (no. 12274031) and the Beijing Institute of Technology Research Fund Program for Teli Young Fellows.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References