Diffusion Entropy and the Path Dimension of Frictional Finger Patterns

Olsen, Kristian Stølevik; Campbell, James Matthew

doi:10.3389/fphy.2020.00083

ORIGINAL RESEARCH article

Front. Phys., 31 March 2020
Sec. Condensed Matter Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00083

Diffusion Entropy and the Path Dimension of Frictional Finger Patterns

Kristian Stølevik Olsen¹^*

James Matthew Campbell^1,2

¹Department of Physics, University of Oslo, Oslo, Norway
²College of Engineering, Swansea University, Swansea, United Kingdom

The authors investigate, using both analytical and numerical methods, the entropy associated with a diffusion process inside frictional finger patterns. The entropy obtained from simulations of diffusion inside the pattern is compared to analytical predictions based on an effective continuum description. The analytical result predicts that the entropy depends in a particular way on the path dimension of the system, which governs the scaling of simple paths in the system. The findings indicates that there is a close analogy between the frictional fingers in the continuum and minimum spaning trees on the lattice, as the path dimension is found, through studies of the entropy, to be close to the defining value for the minimum spanning tree universality class.

1. Introduction

Patterns with complex geometry and topology are ubiquitous in Nature. When transport processes take place inside such patterns, their dynamical properties are typically anomalous due to the non-trivial geometry. The case of anomalous diffusive transport, where the mean-square displacement scales non-linearly with time, has been studied in some detail since the 1980s and remains a popular topic to this day [1–9]. While many of the systems studied in this context are idealized and synthetic, like that of hierarchical fractals, real systems are noisy and often have a geometry that is too complex to be exactly captured by the simplified models. In order to utilize the simplified models, one has to identify the right set of relevant geometric properties when a scaled-up effective continuum description is used. These coarser geometric properties then determine the long-time dynamical properties of diffusing particles in the geometry, like the mean square displacement and the entropy. The entropy associated with anomalous diffusion processes has been studied in some detail in the framework of fractional diffusion equations [10–13]. We here instead consider diffusion with spatially dependent diffusivity, where the analytical form of the diffusivity is linked to the systems geometry. It is the aim of this paper to investigate the entropy for such an effective continuum description of diffusion in frictional finger patterns, and the associated insight it brings into the systems coarser geometric properties.

Fricitonal patterns are space-filling bifurcating two-dimensional geometries that arise due to instabilities in frictional fluids. Experimentally, the frictional finger patterns are produced by preparing a mixture of glass beads and liquid in a Hele-Shaw cell before pumping out of liquid from the center of the cell. When the cell has open ends, this forces air into the glass bead / liquid mixture resulting in a deformation of the boundary of the mixture [14, 15]. The deformation takes place where the energy needed to move the boundary is the smallest. A simulated version of the pattern is shown in Figure 1A, based on the algorithms discussed in Olsen et al. [16].

FIGURE 1

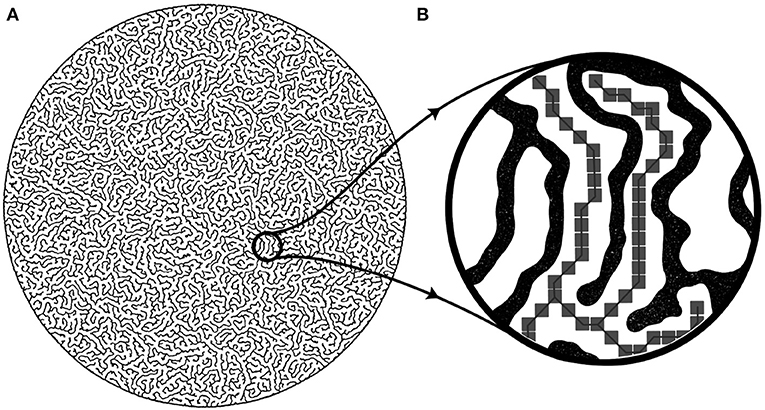
Figure 1. Figure showing a frictional finger pattern (A) together with the one-dimensional skeletonized tree-structure obtained by contracting the finger widths to zero (B). The skeletonized pattern is pixelized before random walkers are released as discussed in section 3.

It was recently hypothesized by the authors that since the frictional finger patterns are formed through a optimal path-finding process it may belong to the geometric universality class of minimum spanning trees (MST)[16]. These are tree-structures constructed on a lattice by assigning a random energy to every lattice link and finding the loopless configuration of links that globally minimizes the total system energy [17]. Universality in this context refers to the exponents reflecting geometric properties of a pattern, like the fractal dimensions d_f or minimum path dimension d_m, the latter being the scaling exponent connecting Euclidean and intrinsic distance measures. Since on loopless structures there is an unique path connecting any two points we will simply refer to d_m as the path dimension. The 2D MST class has d_f = 2 and d_m = 1.22 ± 0.01 [17]. Direct measurements of the path dimension in the frictional fingers have proven to be difficult, due to the noisy and complex nature of the patterns. In particular, the path dimension can be estimated locally by fixing a sample point in the system and considering the average length $\bar{ℓ}$ of paths out to a radius of Euclidean length r. To obtain a global "coarse-grained" estimate $\bar{d_{m}}$ for the path dimension of the system this local path dimension should be averaged over many sample points. This gives a path dimension of $\bar{d_{m}} = 1.25 \pm 0.03$ [16]. The path dimension can also be estimated by treating the pattern as a tree structure and using branching statistics, similar to the study of river networks. This method in stead gives $\bar{d_{m}} = 1.20 \pm 0.03$ [16]. While both of these measurements are consistent with the MST class, they are inconsistent with each other. Rather that directly measuring the path dimension we will here use the diffusing particles as a probe of the system geometry. In particular, since the entropy is a measure of how fast the diffusion process is relaxing toward equilibrium, the entropy will be a function of the systems geometry and will therefore give us some insight into the value of $\bar{d_{m}}$ .

The rest of this paper is outlined as follows. Section 2 discusses the diffusion entropy associated with the effective continuum description, which is based on a simple power-law scaling of the diffusivity. The entropy associated with the corresponding Fokker-Planck equation is calculated analytically and compared to results obtained using fractional diffusion equations. Section 3 discusses a new numerical implementation of random walkers in frictional finger patterns that is expected to increase both efficiency and accuracy. The entropy is calculated, and compared to analytical predictions. Finding the best fit of the analytical prediction as system parameters are varied gives a value for the path dimension. Concluding remarks are offered in section 4.

2. Entropy of the Effective Continuum Description

To study the diffusion process in the frictional finger patterns on a large length scale we use state-dependent diffusion equations where the diffusivity can depend of the particle position. Microscopically, Brownian particles move throughout the pattern with a constant diffusivity. However, the collisions with the walls of the confining geometry affects the macroscopic transport properties. We imagine that after a sort of coarse-graining or homogenization procedure the diffusion process can be described by an overdamped Langevin equation of the form

\begin{array}{l} {\dot{x}}_{a} = \sqrt{2 D (x)} η_{a} (t) & (1) \end{array}

where a is the spatial component of the vector and η is a delta-correlated white noise with $〈 η_{a} (t) η_{b} (t^{'}) 〉 = 2 δ_{a b} δ (t - t)$ . The diffusivity is here assumed to be isotropic but inhomogeneous. When going from a Langevin description on the microscopic scale to an evolution equation for the particle density on the macroscopic scale one has to decide on which stochastic calculus to be used, as discussed in the classical books by Risken [18] and Van Kampen [19]. This problem, known as the Itô-Stratonovich dilemma, results in different forms of the macroscopic equations that differ in the presence of an additional drift term proportional to the gradient of the diffusivity. Recently it has also been showed that these different form of the density evolution equation can be obtained as scaling limits of a random walk on a lattice where inhomogeneities are associated with bonds and/or vertices of the lattice [20].

In the case of diffusion in frictional finger patterns we chose the diffusion law associated with the Hänggi-Klimontovich convention, where no drift term associated with diffusivity gradients are present. This choice of diffusion law together with the Einstein relation was recently used to identify the form of the spatially dependent diffusivity for transport in the frictional fingers, where under an isotropy assumption one has $D (r) = D_{0} r^{- ξ}$ [16]. As is the case for perfectly hierarchical fractals, the exponent ξ is related to the fractal dimensions of the pattern as ξ = d_f − 2 + d_m = d_m, where we used the space-filling property of the finger pattern [1, 16].

The corresponding density evolution equation in the Hänggi-Klimontovich interpretation takes the following form

\begin{array}{l} \partial_{t} ρ (r, t) = \partial_{r} [r D (r) \partial_{r} ρ (r, t)] & (2) \end{array}

This generalized Ficks equation has a well-known solution for radial power-law diffusivity, taking the form [6]

\begin{array}{l} ρ (r, t) = \frac{2 + ξ}{2 π Γ (\frac{d_{s}}{2})} {[\frac{1}{D_{0} {(2 + ξ)}^{2} t}]}^{\frac{d_{s}}{2}} exp (- \frac{r^{2 + ξ}}{D_{0} {(2 + ξ)}^{2} t}) & (3) \end{array}

where d_S = 4/(2 + ξ) is the spectral dimension and the normalization used is ∫ dr(2πr)ρ = 1. This solution is typically thought of as a smoothened out envelope of the discrete set of probabilities associated with the vertices of a fractal, as discussed in the original paper [6]. There are several properties of this solution that are only approximately shared with the actual frictional finger system. For example, the solution is completely isotropic ∂_θρ(r, t) = 0. Since diffusing particles will be forces to move along fingers in our pattern, we know that locally the system is very anisotropic. However, on large time and length scales, the different anisotropies are expected to cancel to produce an approximately isotropic behavior. Furthermore, the solution assumed a single globally well-defined path dimension d_m, while it is known that in noisy real systems this dimension can vary locally. Again we expect that on large space and time scales the inhomogeneities average out, producing a single global path dimension $\bar{d_{m}}$ as discussed in the introduction. The predicted second moment of the solution Equation (3) was tested against the mean-square displacement of random walk simulations in the pattern with reflecting boundary conditions in previous work and was seen to agree well with the simulations, adding to its validity as an effective model [16].

Given the above solution Equation (3) the entropy of the diffusion process can be calculated analytically. What type of entropy we consider is not of great importance here, as long as it is the same entropy that is calculated later in section 3 in the numerical methods. This is because at the end of the day, we are interested in using the numerical measurements of the entropy as an indirect measurement of the path dimension for the frictional fingers. From an information theoretic perspective there are dozens of entropies that could be considered, most of which can be thought of as an analytical continuation of the Shannon-Gibbs entropy which is recovered as some entropic parameter is tuned correctly [21]. We here consider the Shannon-Gibbs formula as it is not only readily calculated but also closer connected to the entropy familiar in extensive thermodynamics.

The Shannon-Gibbs entropy for the particle density takes the form [22]

\begin{array}{l} H [ρ] = - \int d V ρ (x) log ρ (x) . & (4) \end{array}

We will write Equation (3) in the form ρ(r, t) = A(t, ξ) exp (−r^2+ξ/a(t, ξ)) for notational simplicity. According to Equation (4) we then have the entropy in terms of a non-integer moment:

\begin{array}{l} H [ρ (t), ξ] = \frac{〈 r^{2 + ξ} 〉}{a (t, ξ)} - log A (t, ξ) . & (5) \end{array}

Since our distribution is a simple shifted Gaussian a change of variables easily allows us to find this moment. Using the integral

\begin{array}{l} \int_{0}^{\infty} d x x^{μ} e^{- x^{ν} / a} = \frac{a^{\frac{μ + 1}{ν}}}{ν} Γ (\frac{μ + 1}{ν}) . & (6) \end{array}

With μ = 3 + ξ and ν = 2 + ξ, the entropy can be calculated as

\begin{array}{l} H [ρ (t), \bar{d_{m}}] = \frac{2}{2 + \bar{d_{m}}} [1 + log (D_{0} {(2 + \bar{d_{m}})}^{2})] + \\ log [π Γ (\frac{4}{2 + \bar{d_{m}}})] + \frac{2}{2 + \bar{d_{m}}} log t, & (7) \end{array}

where we used $ξ \approx \bar{d_{m}}$ based on the above discussion. Interestingly the associated entropy production $Ḣ = 2 / (t (2 + \bar{d_{m}}))$ has also been obtained by using a two-dimensional diffusion equation with Caputo or Weyl fractional-time derivative [13].

In Equation (7) we see that the global path dimension $\bar{d_{m}}$ determines the temporal evolution of the entropy. As expected, a higher path dimension, meaning a more disordered system geometry, will give a lower entropy production since the diffusion process is more hindered. Using the same integral formula as above it is also easily shown from the solution Equation (3) that the mean-square displacement takes the form

\begin{array}{l} 〈 r^{2} 〉 = \frac{Γ (2 α) {[D_{0} {(2 + \bar{d_{m}})}^{2}]}^{α}}{Γ (α)} t^{α} & (8) \end{array}

where the diffusion exponent is given by $α = 2 / (2 + \bar{d_{m}})$ . Note that the diffusion exponent also governs the temporal scaling of the entropy H ~ α log t.

3. Results From Numerical Simulation

To calculate the numerical entropy we construct a simplified discrete random walk-based model for the diffusion process. To make these simulations more efficient, we make some simplifying assumptions. The biggest simplification comes from applying a topological contraction on the pattern so that the finger widths are set zero, effectively turning the problem into a one dimensional one. The resulting skeletonized version of the pattern, showed in Figure 1B, is what we will release random walkers on. This topological simplification will not change the main geometric features of the pattern, since the folding and connectedness of every branch is conserved.

When performing the numerical simulations the one-dimensional skeletonized pattern is discretized before a discrete random walk process is released. In the resulting discrete "morphological graph" of the pattern there are no additional inhomogeneities associated with transition probabilities over links as all the inhomogeneity we are interested in stems from the pattern itself. In practice, the discretization is obtained by pixelating the skeletonized pattern and treating the pixels as sites for the random walker. A cartoon of the pixels are shown in Figure 1B. A random walker jumps to one of its neighboring pixels, including diagonal neighbors, with equal probability. Since the code is ran with a very large number of particles, we estimate the number of particles that move to a given neighboring pixel according to a binomial distribution. Hence, at every time step we only need as many random numbers as there are neighbors for a given pixel rather than one number for every particle as in traditional random walk methods.

To calculate the entropy numerically we use the Gibbs-Shannon formula for the discrete random walk

\begin{array}{l} H_{num} (t) = - \sum_{pixels i} ρ_{i} (t) log ρ_{i} (t) & (9) \end{array}

where ρ_i(t) is the probability of finding a particle at pixel i at time t. This probability is straightforwardly calculated as the ratio of the number of particles at pixel i at time t to the total number of particles in the system

\begin{array}{l} ρ_{i} (t) = \frac{n_{i} (t)}{N} . & (10) \end{array}

The system is initialized with all particles released at the same position, as the analytical solution assumes a Dirac delta-like initial condition. Figure 2 shows the entropy of the simulation for three different randomly chosen initial positions close to the center of the pattern. We see that while the temporal scaling agrees, they have different zero-point entropies. By inspection of Equation (7) we see that it is possible to have the same temporal scaling but a different zero-point entropy is the diffusion constant D₀ is allowed to vary throughout the system. This may indicate that a more realistic diffusivity is $D (x, y) = D_{0} (x, y) r^{- ξ}$ where D₀ is a slowly varying function taking into account small inhomogeneities in the pattern not captured by the simplified power-law model.

FIGURE 2

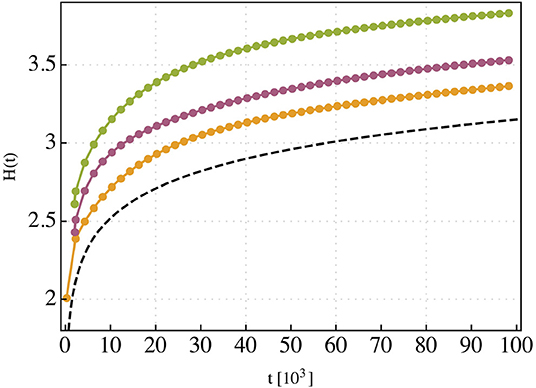
Figure 2. The entropy associated with three randomly chosen initial positions inside the finger pattern. The point were chosen inside a circle of ~50% pattern radius in order to avoid the outer boundaries of the pattern. The dotted line is a reference line 0.62 log₁₀(t).

Figure 3 shows the average entropy $\bar{H} (t) = \sum_{i = 1}^{3} H_{i} (t)$ where i runs over the three different initial positions. The entropy shows a very convincing growth proportional to log t over several decades. The best fit for the slopes of the entropies in Figure 2 is given by α = 0.62. This is consistent with the global estimate of the path dimension $\bar{d_{m}} \approx 1.22$ , which is exactly the path dimension of minimum spanning trees [17]. This value for the path dimension is consistent with the ones obtained in earlier work, although the value obtained through the entropy is much closer to the MST value [16]. This significantly strengthens our belief that the frictional finger pattern lies in the MST universality class and can be seen as a continuum analog of the lattice MST.

FIGURE 3

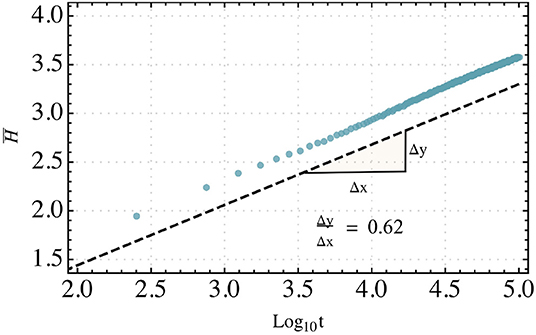
Figure 3. Averaged entropy $\bar{H}$ shown in semi-log scale. The entropy grows with a linear slope of α = 0.62. Since the entropy of the three different initial positions may vary at short times we have ignored the first 20% of the datapoints when performing the linear fit. The slope α = 0.62 is in good agreement with the expected minimum spanning tree value.

4. Conclusion

In this paper we have studied the entropy of diffusion in frictional finger patterns. In addition to being a measure of how fast the non-equilibrium process is evolving, the entropy is also considered as a tool for studying the systems coarser geometry as the diffusing particles explore the large-scale structure at late times. Our results show that the (coarse) path dimension takes a value close to $\bar{d_{m}} = 1.22$ which is the defining value of the minimum spanning tree universality class. This strengthens the current hypothesis that the frictional fingers belong to this class.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

KO performed analytical calculations and wrote the paper. JC developed numerical code crucial for the paper, analyzed the pattern, and aided in the writing process.

Funding

This work was supported by the Research Council of Norway through the Center of Excellence funding scheme, Project No. 262644(PoreLab).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Eirik G. Flekkøy, Luiza Angheluta, and Signe Kjelstrup for insightful input and discussions during this work.

References

1. ben Avraham D, Havlin S. Diffusion and Reactions In Fractals And Disordered Systems. Cambridge: Cambridge University Press (2000). doi: 10.1017/CBO9780511605826

CrossRef Full Text | Google Scholar

2. Bouchaud J-P, Georges A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys Rep. (1990) 195:127–293. doi: 10.1016/0370-1573(90)90099-N

CrossRef Full Text | Google Scholar

3. de Gennes PG. La percolation: un concept unificateur (Percolation a unifying concept). La Recherche. (1976) 919:72–82.

Google Scholar

4. Havlin S, Djordjevic ZV, Majid I, Stanley HE, Weiss GH. Phys Rev Lett. (1984) 53:178. doi: 10.1103/PhysRevLett.53.178

CrossRef Full Text

5. Havlin S, Kiefer JE, Weiss GH. Anomalous diffusion on a random comblike structure. Phys Rev A. (1987) 36:1403. doi: 10.1103/PhysRevA.36.1403

PubMed Abstract | CrossRef Full Text | Google Scholar

6. O'Shaughnessy B, Procaccia I. Analytical solutions for diffusion on fractal objects. Phys Rev Lett. (1985) 54:455. doi: 10.1103/PhysRevLett.54.455

PubMed Abstract | CrossRef Full Text | Google Scholar

7. B'nichou O, Illien P, Oshanin G, Sarracino A, Voituriez R. Diffusion and subdiffusion of interacting particles on comblike structures. Phys Rev Lett. (2015) 115:220601. doi: 10.1103/PhysRevLett.115.220601

CrossRef Full Text | Google Scholar

8. Tamm MV, Nazarov LI, Gavrilov AA, Chertovich AV. Anomalous diffusion in fractal globules. Phys Rev Lett. (2015) 114:178102. doi: 10.1103/PhysRevLett.114.178102

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tan P, Liang Y, Xu Q, Mamontov E, Li J, Xing X, et al. Gradual crossover from subdiffusion to normal diffusion: a many-body effect in protein surface water. Phys Rev Lett. (2018) 120:248101. doi: 10.1103/PhysRevLett.120.248101

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hoffmann KH, Essex C, Schulzky C. Fractional diffusion and entropy production. J Non Equilib Thermodyn. (1998) 23:166–75. doi: 10.1515/jnet.1998.23.2.166

CrossRef Full Text | Google Scholar

11. Essex C, Schulzky C, Franz A, Hoffmann KH. Tsallis and R'nyi entropies in fractional diffusion and entropy production. Physica A Stat. Mech. Appl. (2000) 284:299–308. doi: 10.1016/S0378-4371(00)00174-6

CrossRef Full Text | Google Scholar

12. Li X, Essex C, Davison M, Hoffmann KH, Schulzky C. Fractional diffusion, irreversibility and entropy. J Non Equilib Thermodyn. (2003) 28:279–91. doi: 10.1515/JNETDY.2003.017

CrossRef Full Text | Google Scholar

13. Aghamohammadi A, Fatollahi AH, Khorrami M, Shariati A. Entropy as a measure of diffusion. Phys Lett A. (2013) 377:1677–81. doi: 10.1016/j.physleta.2013.05.015

CrossRef Full Text | Google Scholar

14. Sandnes B, Knudsen HA, Måløy KJ, Flekkøy EG. Labyrinth patterns in confined granular-fluid systems. Phys Rev Lett. (2007) 99:038001. doi: 10.1103/PhysRevLett.99.038001

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Knudsen HA, Sandnes B, Flekkøy EG, Maåløy KJ. Granular labyrinth structures in confined geometries. Phys Rev E. (2008) 77:021301. doi: 10.1103/PhysRevE.77.021301

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Olsen KS, Flekkøy EG, Angelutha L, Campbell JM, Maåløy KJ, Sandnes B. Geometric universality and anomalous diffusion in frictional fingers. N J Phys. (2019) 21:063020.

Google Scholar

17. Dobrin R, Duxbury PM. Minimum spanning trees on random networks. Phys Rev Lett. (2001) 86:5076. doi: 10.1103/PhysRevLett.86.5076

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Risken H. The Fokker-Planck Equation. Berlin; Heidelberg: Springer-Verlag (1984). doi: 10.1007/978-3-642-96807-5

CrossRef Full Text | Google Scholar

19. Van Kampen NG. Stochastic Processes in Physics and Chemistry, Vol. 1. Amsterdam: Elsevier (1992).

Google Scholar

20. Andreucci D, Cirillo ENM, Colangeli M, Gabrielli D. Fick and fokker-planck diffusion law in inhomogeneous media. J Stat Phys. (2019) 174:469. doi: 10.1007/s10955-018-2187-6

CrossRef Full Text | Google Scholar

21. Rapisarda A, Thurner S, Tsallis C. Nonadditive entropies and complex systems. Entropy. (2019) 21:538. doi: 10.3390/e21050538

CrossRef Full Text | Google Scholar

22. Wehrl A. The many facets of entropy. Rep Math Phys. (1991) 30:119–29. doi: 10.1016/0034-4877(91)90045-O

CrossRef Full Text | Google Scholar

Keywords: entropy, anomalous diffusion, universality, fractal geometry, frictional finger pattern, pattern analysis

Citation: Olsen KS and Campbell JM (2020) Diffusion Entropy and the Path Dimension of Frictional Finger Patterns. Front. Phys. 8:83. doi: 10.3389/fphy.2020.00083

Received: 09 January 2020; Accepted: 09 March 2020;
Published: 31 March 2020.

Edited by:

Giancarlo Ruocco, Center for Life NanoScience (IIT), Italy

Reviewed by:

Matteo Colangeli, University of L'Aquila, Italy
Constantinos Simserides, National and Kapodistrian University of Athens, Greece

Copyright © 2020 Olsen and Campbell. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Kristian Stølevik Olsen, k.s.olsen@fys.uio.no

ORIGINAL RESEARCH article

Diffusion Entropy and the Path Dimension of Frictional Finger Patterns

1. Introduction

2. Entropy of the Effective Continuum Description

3. Results From Numerical Simulation

4. Conclusion

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

Acknowledgments

References

This article is part of the Research Topic

People also looked at