Dual Set-Membership State Estimation for Power Distribution Networks Under Event-Triggered Mechanism

1 Introduction

In recent years, the operation and control of power distribution networks (PDNs) are facing severe challenges with the large access of flexible loads and renewable energy (Dehghanpour et al., 2018; Fang et al., 2020; Zhang and Wang, 2020). In order to improve the power quality, the distribution management system (DMS) is required to achieve a higher level of control and management for the PDNs. As the basis of the smart grid situation perception, the state estimation module is the core part of the DMS. By using real-time measurement data, the operation state of the system can be estimated, and its accuracy directly determines the dispatching and control ability of the DMS to PDNs.

The traditional static state estimation completely depends on the measurement set at a certain time to obtain the operation state of the system at that time, ignoring the change process of thesystem state in continuous time (Jin et al., 2020). By contrast, dynamic state estimation is to track the changes of system states by recursive update estimation, and another advantage is that it can predict the state of the next time. Therefore, it is more conducive to improve the management level of DMS and has attracted the extensive attention of researchers (Wang et al., 2020; Ji et al., 2021). So far, the estimation methods based on the Kalman filtering framework have been widely applied in the dynamic state estimation of PDNs, such as extended Kalman filter (EKF), unscented Kalman filter (UKF), and robust recursive Kalman filter (RKF). Specifically, aiming at the state estimation problem of nonlinear systems, the EKF linearizes the nonlinear equation by the Taylor series and truncates it to the first order. Nevertheless, large errors will be produced for some strongly nonlinear systems due to the ignoring of higher-order remainder terms (Zhao et al., 2016; Ćetenović et al., 2021). Differently, the UKF directly obtains the approximate probability distribution of nonlinear function with the help of unscented transform technique (Zhao and Mili, 2017; Bai et al., 2021b), which avoids the linearization process and fully considers the influence of the higher-order terms. The RKF can deduce the filter gain by solving the upper bound of the error covariance matrix, and the higher-order remainder is expressed by a combination of uncertain linear matrices. It has been proved that the estimation accuracy is significantly improved by considering the influence of linearization error (Bai et al., 2018; Tan et al., 2021).

It is worth noting that the abovementioned filtering algorithms are all designed based on the assumption that the system noises obey Gaussian distribution. Actually, in the engineering practice, the statistical characteristics of the PDNs noises are unknown, which will inevitably bring errors to the estimation results (Wang et al., 2017). Fortunately, although the statistical characteristics of the PDNs noises are unknown, their boundaries are usually easy to obtain. For example, the dynamic modeling error of the state space model can be restricted by a known interval, and the measurement errors of phasor measurement units (PMUs) are described as less than one percent of the total vector errors according to the IEEE standards (Martin et al., 2008; Qing et al., 2013). To deal with such unknown but bounded (UBB) noises, the set-membership filtering algorithm has been proposed by Schweppe (1968), and its main idea is to provide a set of state estimation that always contains the real states of the system (Cerone et al., 2014). In order to facilitate the description, the state estimation set is usually outsourced using regular geometry, such as ellipsoid (Calafiore, 2005; Ding et al., 2019), zonotope (Kühn, 1998; Alamo et al., 2005), and box (Ping et al., 2020). And the ellipsoid set becomes the geometric representation tool selected in this article due to its simple representation and smooth derivable boundary. After years of development, the results of the set-membership filtering algorithm in linear systems have been widely published (Becis-Aubry et al., 2008; Gubarev and Melnichuk, 2015; Liu et al., 2016). To realize the application of the set-membership theory in nonlinear systems, the nonlinear set-membership filtering algorithm has been developed (Scholte and Campbell, 2003; Calafiore, 2005) and widely applied in various fields, such as target tracking (Yu et al., 2016; Bai et al., 2021a), generator state estimation (Cheng et al., 2018), and power system state estimation (Qing et al., 2013; Zhang et al., 2020). In addition, what should be concerning is how to obtain the compact bound of the linearization error for strongly nonlinear systems. In this regard, the extended set-membership filter (ESMF) has been developed in Scholte and Campbell (2003), in which the interval analysis method is used to determine the uncertain boundary of linearization error. However, this method will increase the conservatism of boundary estimation. Here, we try to solve the tighter linearized error boundary by the semi-infinite programming approach (Vandenberghe and Boyd, 1996). Specifically, firstly, the dual form of semi-infinite programming is derived by the known lemma. Then, the continuous measure is discretized and approximated by random sampling technology (Wang et al., 2018) (e.g., the Monte Carlo sampling method), such that the discrete expressions of the compact linearized error boundary ellipsoid center and shape matrix can be obtained recursively.

From another perspective, the measurement and communication technologies have been developed rapidly in recent years. In comparison with the conventional distribution remote terminal units (DRTUs), the PMUs can accurately measure the phasor of voltage and current, and high-frequency sampling provides a lot of real-time system information for dynamic state estimation, which is more conducive to the implementation of dynamic state estimation (Zhang et al., 2020; Mohammadrezaee et al., 2021; Qu et al., 2021). However, due to the limited bandwidth of the information communication network (ICN), the transmission of large amounts of data inevitably leads to certain network-induced phenomena such as channel congestion and communication delay (Wei et al., 2015; Hu et al., 2020). In order to alleviate the transmission pressure of the ICN, the researchers have proposed many effective solutions (Ge et al., 2017; Peng and Li, 2018; Liu et al., 2019; Zou et al., 2021). Among them, the event-triggered mechanism has recently attracted increasing research interest in the field of power systems (Liu et al., 2017; Bai et al., 2021b; Cheng and Bai, 2021).

Different from the traditional time-based periodic transmission mechanism, event-triggered transmission mechanism refers to using the constructed trigger function to judge whether the measurement at the current time meets the trigger requirements, and only the data that meet the specific conditions are transmitted to the estimator for processing. It can effectively reduce the communication frequency and improve the communication efficiency while ensuring the PDNs state estimation performance. Nonetheless, so far, the problem of dynamic state estimation for the PDNs based on the event-triggered mechanism has not been fully studied considering nonlinear and unknown but bounded noises, which is the main motivation of our research.

In view of the above discussion, we aim to design a dual set-membership filtering algorithm for the PDNs state estimation under the event-triggered mechanism to achieve a balance of network resource utilization and system filtering performance. The main technical contributions for this article can be summarized as follows:

1) An event-triggered mechanism suitable for PDNs data transmission is proposed, which can reasonably reduce the data transmission frequency on the premise of ensuring the accuracy of state estimation, so as to provide a feasible method to alleviate the communication pressure and save network resources;

2) With the help of random sampling technique, the compact linearized error ellipsoid is obtained by solving the dual problem of nonlinear programming to reduce the conservatism of the set-membership filtering algorithm;

3) Based on recurrent linear matrix inequality (RLMI) and convex optimization theories, sufficient conditions for the existence of the estimated ellipsoid are derived, and the time-varying gain matrix is solved. Then, an event-triggered dual set-membership filter (ET-DSMF) is developed to realize the online state monitoring of the system and further improve the perception ability of the PDNs.

The contents of the article are organized as follows: Section 2 establishes the dynamic state model of the PDNs. Section 3 proposes the event-triggered mechanism. Section 4 mainly introduces the calculation method of the compact boundary of the linearization errors, and a dual set-membership filter based on the event-triggered mechanism is designed. In Section 5, The IEEE 13 PDN test system serves as an example to verify the effectiveness of the filtering algorithm proposed in this article. Finally, we summarize this article in Section 6.

2 System Model of Power Distribution Networks

In the dynamic state estimation of the PDNs, the system model is utilized to estimate the operation states at the current and predict the state changes at the next. In abstract, the system model of the PDNs includes the state model and measurement model, and its general model can be expressed by Eq. 1:

where $x_k\in {\mathbb{R}}^n$ and $y_k\in {\mathbb{R}}^m$ are the system state vector and the measurement vector, respectively. $x_k={[U_1,\dots ,U_i,\dots ,U_N]}^T$ and the element is specifically expressed as $U_i=[U_i^{re,a},U_i^{im,a},U_i^{re,b},U_i^{im,b},U_i^{re,c},U_i^{im,c}]$. N denotes the number of system buses. $U_i^{re,p}$ and $U_i^{im,p}(p\in \{a,b,c\})$ represent, respectively, the p-phase real and imaginary voltage at the ith bus. f(⋅) and h(⋅) are the state transfer equation and the measurement equation, respectively. In addition, the system noises and initial state values satisfy the following assumptions:

Assumption 1. The noise sequence ω_k and v_k satisfy the following ellipsoid constraints:

where $Q_k\in {\mathbb{R}}^{n\times n}$ and $R_k\in {\mathbb{R}}^{m\times m}$ are known symmetric positive definite matrices.

Assumption 2. The initial state x₀ belongs to the initial state ellipsoid ϕ₀ and defined as

where ${\widehat{x}}_0$ is the center for the estimation set and $P_{\text{0}}\in {\mathbb{R}}^{n\times n}$ is the symmetric positive definite matrix describing the shape and orientations for the initial state ellipsoid.

2.1 State Model

In this article, the system is assumed in a quasi-steady state operation, and a widely used dynamic model is adopted to represent the equation of state:

where A_k is the state transfer matrix, which represents the speed of the state transfer; B_k is the input matrix, reflecting the changing trend in the state trajectory. The Holt-Winters two-parameter exponential smoothing method is employed to compute A_k and B_k online.

subject to

in which, α and β indicate smoothing parameters, taking the values between 0 and 1; ${\widehat{x}}_{k|k-1}$ is the state prediction value at k − 1; and ${\widehat{x}}_k$ is the state estimate value at k.

2.2 Measurement Model

At present, hybrid measurements with DRTUs and PMUs are adopted in the PDNs to coordinate the economy of power network construction and the accuracy of state estimation. The use of various measurement devices increases the measurement redundancy and then provides reasonable measurement data for the PDNs state estimation. The DRTU measurements are expressed as

where ${\vec{U}}_{i-j}^{re,q}=U_i^{re,q}-U_j^{re,q},{\vec{U}}_{i-j}^{im,q}=U_i^{im,q}-U_j^{im,q},$$P_{i-j}^p$ and $Q_{i-j}^p$ are the p-phase active and reactive power flow measurements at the i − j branch, respectively. $P_i^p$ and $Q_i^p$ are the p-phase active and reactive power injection measurements at the ith bus, respectively. $b_{i-j}^p$ represents p-phase ground guide at the i − j branch. γ_j−i is a scalar describing the mutual coupling between the network nodes. If Θ represents the set of neighbor nodes of node i, then

Besides, the PMU measurements are expressed as

where $I_{i-j}^{re,p}$ and $I_{i-j}^{im,p}$ represent the p-phase real and imaginary currents at the i − j branch, respectively.

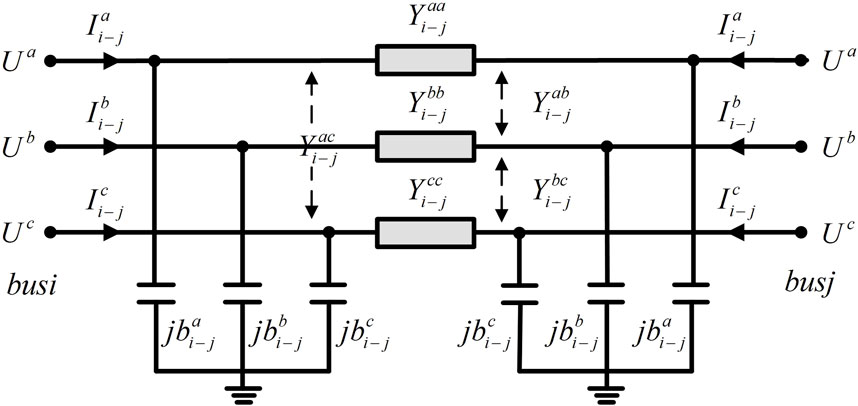
Figure 1 shows the three phase unbalanced line model of the PDNs, where the missing phase line model is similar to the three-phase model and is not fully shown here.

FIGURE 1. Three-phase unbalanced line model of the PDNs.

3 Event-Triggered Mechanism

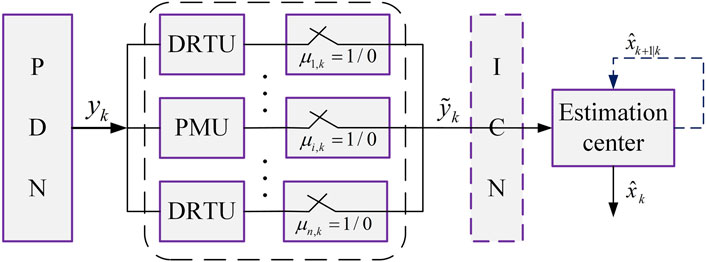
The basic working architecture of the PDN based on an event-triggered mechanism is shown in Figure 2. To be specific, the measurement at the current moment collected using the PMU and DRTU measurement devices are compared with the measurement of the latest transmission by the event-triggered mechanism. When the triggering condition is satisfied, the current measurement will be transmitted to the remote estimation center via the ICN, otherwise the measurement will not be transmitted. According to the zero-order hold strategy, the last transmitted measurement will participate in the state estimation process in the estimation center. Since the event-triggered mechanism is adopted, the measurement devices only provide useful information to the estimation center, and the data transmitted by the ICN will greatly decrease, which reasonably alleviates the burden on the channel. Thus, the probability of network-induced phenomenon is effectively reduced.

FIGURE 2. Event-triggered mechanism.

The triggering condition is as follows:

The specific expression of S_k is

where ψ is the weight matrix of the opposite and positive definite and is assumed to be a unit matrix in this article. σ_i,k is the difference between the current measurement y_i,k and the last transmitted value $y_{i,t_r^i}$ (the latest accepted values for the estimate center), which is defined as

and the following expression is given by:

When increasing the value of ɛ_i, the transmission frequency would decrease correspondingly. In engineering practice, the selection of ɛ_i should consider not only the network communication resources but also the system filtering performance. As such, the appropriate parameter selected can achieve a trade-off between energy conservation and the estimation performance of the distribution system. Then, the event-triggering function can be defined as follows:

The parameters μ_i,k are constructed to indicate whether the measurement is transmitted or not, and triggering logic variable is expressed as

If μ_i,k = 1, the event triggering is executed. Otherwise, by the zero-order hold strategy, the latest triggered one would be used to the filtering process instead of y_i,k, so as to realize the measurement synchronization and the integrity of the measurement information. By Equations 17, 18, the non-triggering error can be described as

The current measurement information received by the estimation center is

where ${\sigma }_k={[{\sigma }_{1,k}^T,{\sigma }_{2,k}^T,\dots ,{\sigma }_{m,k}^T]}^T$.

Let $\delta ={\sum }_{i=1}^m{\delta }_i$, then the formula is established as

The above results will be fully reflected in the design process of the filter.

Remark 1. The different measurement devices such as the PMUs and DRTUs are equipped at the buses of the PDNs. The diversity of measurements will bring great challenges to the setting of event-triggering threshold. Based on this challenge, we develop the event-triggered mechanism described above. This is a relative event-triggered mechanism, which is different from the absolute one in Bai et al. (2021b).

4 Event-Triggered Dual Set-Membership Filter

4.1 Linearization Error Boundary

Actually, the linearization error boundary determined by the interval analysis method is too conservative, and its cumulative effect will also affect the accuracy and even lead to filter divergence. In addition, the Lagrange remainder of the linearized nonlinear function can be used to represent the linearization error, but the process of optimizing the Hessian matrix is more complex. In this article, the linearization error is limited by solving the dual form of semi-infinite programming, which not only avoids the solution of Hessian matrix but also overcomes the defects of the interval analysis method, and a more compact linearization error boundary can be obtained.

A lemma will first be introduced for the formula derivation in this section.

Lemma 1. Wang et al. (2021) The optimization problem of the ellipsoid can be expressed as

with

Then, the optimal solution of Eq. 22 is

where ${\widehat{u}}^{*}={\int }_{\mathbb{C}}ud{\tau }^{*}$ is the optimal solution to the following optimization problem:

with $\stackrel{⌣}{u}={[u^T,1]}^T$, and Eq. 25 is the dual problem of Eq. 22. For the proof of this lemma, please refer to Wang et al. (2021).

Next, we introduce the specific application of this lemma in this article. First, the Taylor expansion of the measurement equation is performed around ${\widehat{x}}_{k+1|k}$.

According to the properties of the ellipsoid, Eq. 26 is equivalent to:

where $‖z_{k+1|k}‖\le 1$, $P_{k+1|k}=E_{k+1|k}{E}_{k+1|k}^T$. Thus, the higher-order linearization error can be expressed as

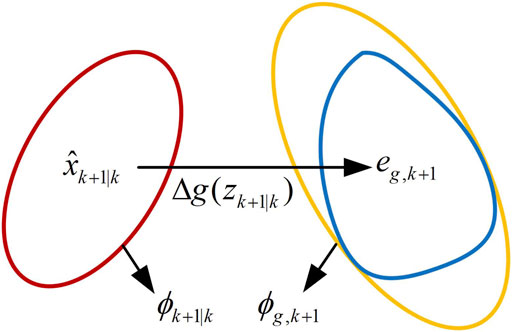
As shown in Figure 3, we try to find a compact ellipsoid to cover the higher-order remainder term, assuming that the outsourced ellipsoid of the higher-order remainder term is expressed as ϕ_g,k+1. This article uses the nonlinear programming method to optimize the boundary of linearization error, which can get a tight boundary estimate. In general, it can be obtained from Lemma 1 that the linear programming Eq. 25 is the dual form of the nonlinear programming Eq. 22. Therefore, in order to achieve a balance between the estimation accuracy and the calculation amount, the continuous system is discretized by the Monte Carlo sampling method. In this regard, the nonlinear programming is converted into a linear programming problem. The following expression is established:

where ${\widehat{u}}_{\text{g},k+1}$ and P_g,k+1 denote the center and shape matrix of the ellipsoid ϕ_g,k+1, respectively.

A nonlinear programming method can be used to optimize the linearized error boundary, so the following nonlinear programming problem can be constructed:

where $\mathbb{C}$ is defined as

in which, h(⋅) is an arbitrary nonlinear continuous function, expressed here as a higher-order remainder term function.

The minimal volume of the linear error outsourcing ellipsoid can be obtained by solving the nonlinear programming problem. In order to make it more convenient, the continuous system is discretized by the Monte Carlo sampling method, and the discrete expression of the center and shape matrix of the ellipsoid are obtained by Eqs. 32, 33, which corresponds to Eq. 24 under continuous form. Moreover, the approximate expression of Eq. 25 is obtained, as shown in Eq. 34. Thus, an outsourcing compact ellipsoid with the linearization error is developed. The results obtained in this section will be used in the design of the dual set-membership filter. The specific process will be shown in detail in Section 4.2.

with

where coefficients τ_i(i = 1, … , m) are obtained by solving the linear programming shown in the solution Eq. 34

By Lemma 1, we obtain the dual form of nonlinear programming and the continuous expressions of the center and shape matrix of the linearized error ellipsoid. Then, the continuous system is discretized by the Monte Carlo sampling method, and the semi-infinite programming problem is transformed into a finite programming problem, so the discrete expressions of the ellipsoid center and shape matrix are obtained.

FIGURE 3. The linearization error ellipsoid.

Remark 2. Different from the UKF, the approximate probability distribution of the nonlinear function cannot be obtained directly, since we assume that the true state is restricted to the ellipsoid, rather than obeying a particular Gaussian distribution. Wang et al. (2021) avoids the process of Taylor expansion by directly solving the approximate distribution of the nonlinear measurement function values. But this will still inevitably produce large errors for strong nonlinear systems. Therefore, the method in this article strikes a balance between the computational quantity and the estimation accuracy.

4.2 Predictive and Update Steps

In this section, a set-membership filtering algorithm based on the event-triggered mechanism is proposed to solve the state estimation problem of the PDNs. And the real state is always confined to the set of state estimation. In order to deal with quadratic constraints such as event-triggered mechanism and external noises, RLMI technology is used to transform the externally bounded ellipsoid filtering problem into a convex optimization problem with linear matrix inequality constraints. The sufficient conditions for the existence of the estimated state set are strictly derived, and the filter gain parameters are easily obtained by solving the convex optimization problem(Boyd et al., 1994).

We begin by introducing two lemmas, which will be used in the proof of this section.

Lemma 2. (S-Procedure) (Bai et al., 2021a): Let ℏ₀(⋅), ℏ₁(⋅), …, ℏ_p(⋅) be the quadratic function of the variable $\chi \in {\mathbb{R}}^n$, ℏ_i(χ) = χ^TM_iχ(i = 0, 1, … , p), with $M_i=M_i^T$, if there exist λ₁⩾0, … , λ_p⩾0 such that $M_0-{\sum }_{i=1}^p{\lambda }_i{M}_i⩽0$, then the following is true: ℏ₁(χ)⩽0, … , ℏ_p(χ)⩽0 → ℏ₀(χ)⩽0.

Lemma 3. (Schur Complement Equivalence) (Bai et al., 2021a): For matrices H₁, H₂, H₃, where $S_1=S_1^T⩾0$, $H_2=H_2^T⩾0$, $H_3^T{H}_2^{-1}{H}_3+H_1⩽0$, if and only if $\left[\begin{array}{cc}\hfill -H_2\hfill & \hfill H_3\hfill \\ \hfill H_3^T\hfill & \hfill H_1\hfill \end{array}\right]<0$ or $\left[\begin{array}{cc}\hfill H_1\hfill & \hfill H_3^T\hfill \\ \hfill H_3\hfill & \hfill -H_2\hfill \end{array}\right]<0$.

One-step state prediction value ${\widehat{x}}_{k+1|k}$ is approximated by the Holt-Winters two-parameter exponential smoothing method. Based on the state estimate at k, one-step predicted ellipsoid ϕ_k+1|k is obtained by solving the semi-definite programming problem Eq. 36.

where P_k+1|k is the desired optimization variable.

It should be noted that calculating the volume of the ellipsoidal set is more difficult than the trace of the matrix P_k+1. The trace of P_k+1 is the sum of the semi-axes of the ellipsoid, by which the size of the ellipsoidal set can be reflected effectively. Therefore, the objective function Eq. 36 is the trace function.

where

Proof 1. In view of Equation 4, we can get one-step prediction state error

Let, $\zeta ={[1,z_k^T,w_k^T]}^T$. Thus, x_k+1 ∈ ϕ_k+1|k is equivalent to

The following unequal conditions exist naturally:

Eq. 41 is equivalent to

By means of Lemma 1, ${\zeta }^T[{\mathrm{\Phi }}_{k+1|k}^T{P}_{k+1|k}^{-1}{\mathrm{\Phi }}_{k+1|k}]\zeta \le 1$ holds, if positive scalar λ₁, λ₂ exists such that

Equation 43 can be rewritten as

where

By Lemma 2, Equation 45 can be converted to the following formula:

The proof is completed.

On the other hand, based on the proposed event-triggered mechanism, the estimates can be expressed by:

where K_k+1 is the filter gain matrix to be solved. In addition, the estimated ellipsoid ϕ_k+1 is obtained by solving the semi-definite programming problem, based on the one-step state prediction value at k.

The optimal variable P_k+1 and the gain matrixes K_k+1 can be obtained by solving the following optimization problem:

where

Proof 2. According to Eq. 47,

with

Thus, x_k+1 ∈ ϕ_k+1 is equivalent to ${\eta }^T[{\mathrm{\Phi }}_{k+1}^T{P}_{k+1}^{-1}{\mathrm{\Phi }}_{k+1}]\eta ⩽1$. The following conditions are naturally satisfied:

which can be rewritten as follows:

It can be seen from Lemma 1 that Eq. 48 is established if positive scalar λ₃, λ₄, λ₅, λ₆, λ₇ exists to make the following inequality hold:

Equation 45 is equivalent to

where

Using Lemma 2, the following inequality relationship holds:

The proof is completed.

In order to more clearly show the filtering algorithm in this article, the ET-DSMF algorithm is summarized as in Algorithm 1.

Algorithm 1. ET-DSMF Algorithm.

Remark 3. It is worth mentioning that the filtering algorithms under the Kalman framework are studied based on the assumption that the noises obey Gaussian distribution (Yang and Li, 2009). However, because the distribution network is located at the end of the power system and there is serious electromagnetic interference, the above assumption is not in line with the actual project. In fact, compared with the statistical characteristics of noises, it is easier for us to know its boundaries. Fortunately, set-membership filtering can effectively deal with this unknown but bounded noises and provide an estimation set that always surrounds the real states.

Remark 4. In order to alleviate communication pressure and improve the induction phenomenon of measurement data in the transmission process, the event-triggered mechanism is integrated into the design of the set-membership filter. To tackle the effects of σ_k, we employ the prescribed triggering condition which can be rewritten as a quadratic constraint. Subsequently, by using S-procedure, this quadratic constraint can be easily dealt with and reflected in the obtained RLMIs. And the gain matrix and the filter of the optimal estimated ellipsoid are obtained by solving the convex optimization problem.

5 Simulation

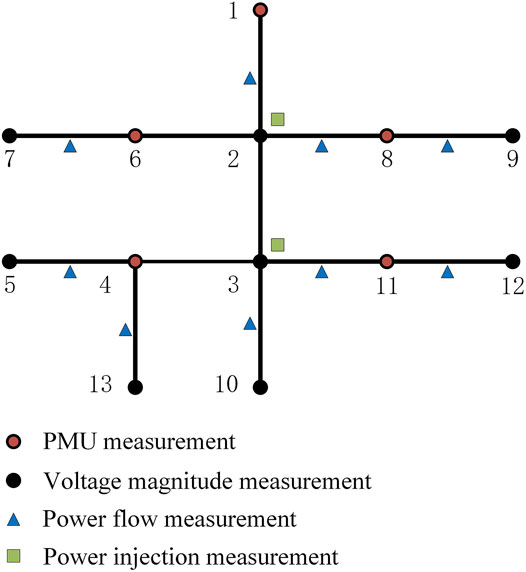
In this section, The IEEE 13 PDN test system is employed for simulation to verify the effectiveness of the ET-DSMF algorithm. The algorithm is implemented in MATLAB R2018b. The topology and the nominal data of the network are obtained from Kersting (1991). The measurement configuration is shown in Figure 4, where the PMUs are deployed at buses 1, 4, 6, 8, and 11. At the beginning, the power flow calculation result is taken as the real value of the state, and the measurement is obtained by superimposing the corresponding UBB noise on the power flow calculation result of the online test system. Moreover, the process equation is obtained by the Holt-Winters two-parameter exponential smoothing method with α = 0.9, β = 0.1. Let the shape matrix of the initial state be P₀ = 4 × 10⁻³I. The process noise is set as Q_k = 6 × 10^–3, and measurement noise parameters are set as $R_k^{PMU}=2\times 10^{-6}$ and $R_k^{DRTU}=2\times 10^{-4}$, respectively. Furthermore, the mean square error (MSE) is introduced in this article to more intuitively reflect the accuracy of the state estimation, i.e., $\text{MS}{\text{E}}_i(k)=(1/k_{\max }){\sum }_{k=1}^{k_{\max }}{(x_{i,k}-{\widehat{x}}_{i,k})}^2$, where k_max represents the number of samples. The transmission rate is defined as the number of transmission measurements divided by all sampling times and described by variables κ.

FIGURE 4. IEEE 13 PDN test system.

5.1 Comparison of Dual Set-Membership Filter and Extended Set-Membership Filter

Figures 5–7 show the performance of the DSMF and ESMF algorithms, taking the simulation results of a-phase at bus 4 as an example. It can be seen that both algorithms can achieve good estimation results. However, the MSE generated by the method proposed in this article is smaller. As shown in Figure 7, although the estimated boundaries obtained by the two algorithms can contain the real state, the proposed algorithm is less conservative owing to considering the compact linearization error ellipsoid. It is obvious that the boundary obtained by the DSMF algorithm is more compact than that obtained by the ESMF.

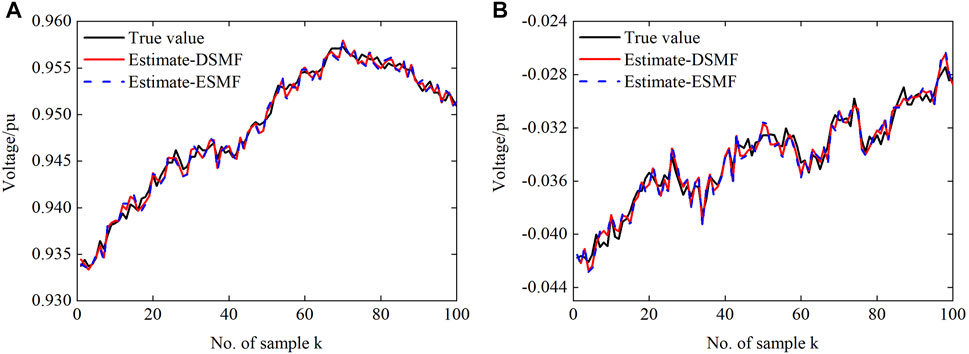
FIGURE 5. The true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.

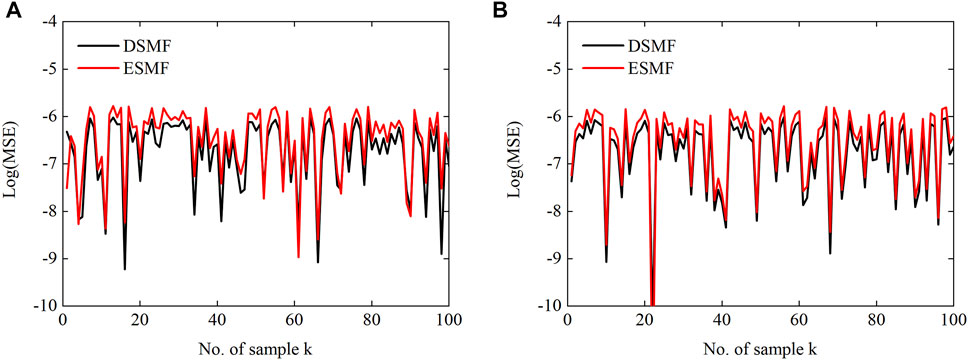
FIGURE 6. Log(MSE) between the true and estimated values of a-phase at bus 4 for the DSMF and ESMF algorithms: (A) the real part of the voltage and (B) the imaginary part of the voltage.

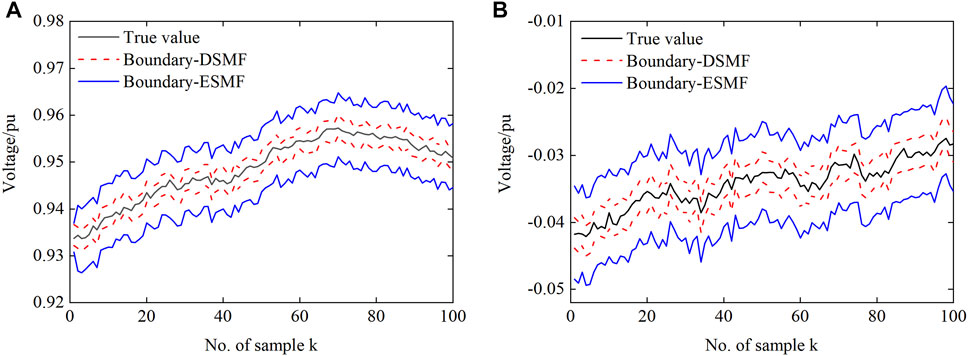
FIGURE 7. Boundaries between the true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.

5.2 Verification of Event-Triggered Dual Set-Membership Filter Algorithm

Firstly, the event-triggering threshold is set as ɛ_i = 5 × 10^–6. Figure 8 shows the state estimation ellipsoid center and boundary of the ET-DSMF algorithm, where κ = 83%. Although the estimation performance of the proposed algorithm degrades at a lower transmission rate, it ensures that the real state always resides in the estimation ellipsoid because the effective information is transmitted to the estimation center. In order to show the filtering results more clearly, Figure 9 shows the MSEs generated by the proposed algorithm. It can be seen that the estimation error is always below the minimum upper bound and close to the upper bound, which further shows the low conservatism of the proposed algorithm.

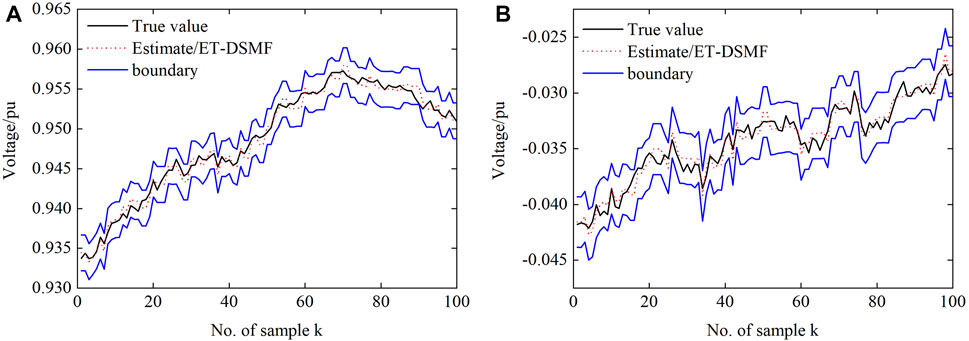
FIGURE 8. The true and estimated values of a-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.

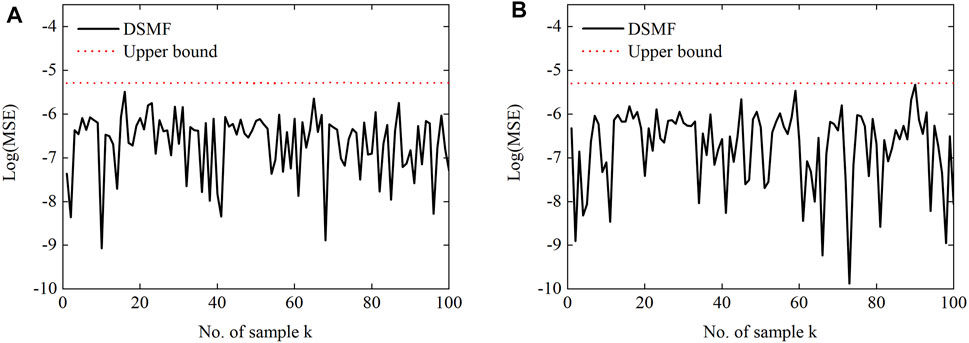
FIGURE 9. Log(MSE) between the true and estimated values of a-phase at bus 4 for the ET-DSMF algorithm: (A) the real part of the voltage and (B) the imaginary part of the voltage.

5.3 Influence of Different Triggering Threshold Parameters

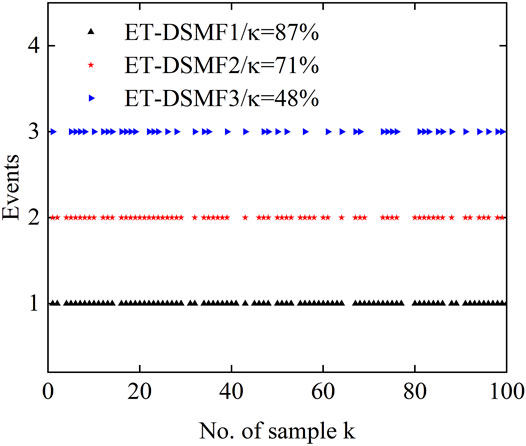
In order to verify the influence of the different triggering thresholds on the performance of the ET-DSMF algorithm, different triggering threshold parameters are selected, i.e., ET-DSMF1 with ɛ_i = 4 × 10^–6, ET-DSMF2 with ɛ_i = 6 × 10^–6, and ET-DSMF3 with ɛ_i = 8 × 10^–6. Figure 10 and Figure 11 show the filtering curves and MSEs of c-phase at bus 4 under three different threshold parameters. In addition, to more clearly show the triggering time, the triggering sequences is shown in Figure 12. With the increase of the triggering threshold, the MSE of the ET-DSMF algorithm increases and the data transmission data decreases accordingly. Therefore, selecting the appropriate triggering threshold parameters can effectively alleviate the pressure of network communication and reduce the probability of network-induced phenomenon.

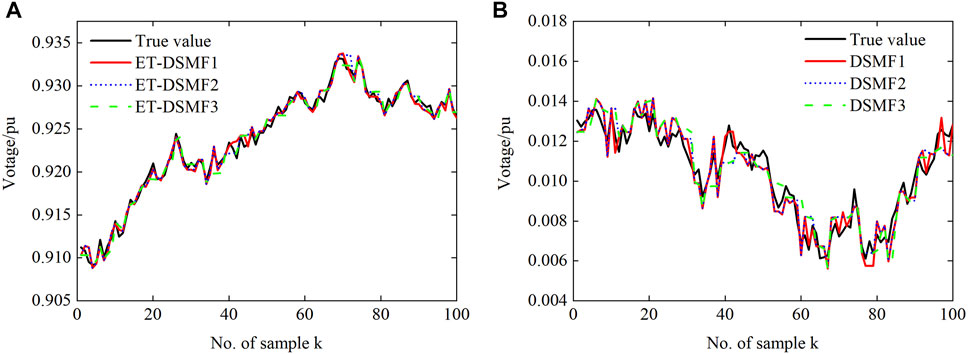
FIGURE 10. The true and estimated values of c-phase at bus 4: (A) the real part of the voltage and (B) the imaginary part of the voltage.

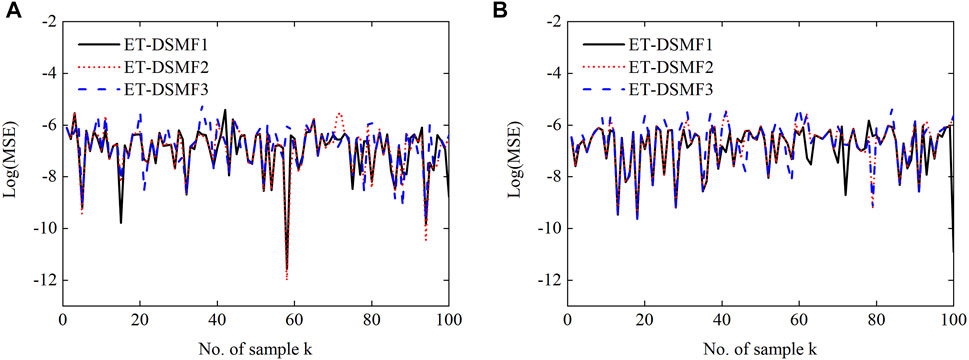
FIGURE 11. Log(MSE) between the true and estimated values of c-phase at bus 4 for the ET-DSMF algorithm: (A) the real part of the voltage and (B) the imaginary part of the voltage.

FIGURE 12. Triggering sequences under different triggering threshold parameters.

6 Conclusion

In this article, an event-triggered dual set-membership filtering algorithm is proposed. Firstly, considering the uncertainty caused by the linearization error, the approximate distribution range of linearization error is determined by the random sampling method, and the compact ellipsoid boundary of the linearization error is obtained by solving the dual problem of the semi-infinite programming, so as to reduce the conservatism of error boundary. Then, an event-triggered mechanism is introduced to reduce the communication burden. Finally, sufficient conditions for the existence of filter parameters are derived by lemmas, and the optimal state feasible set with ellipsoid as boundary is obtained by the semi-definite programming method. The simulation results show that the proposed method can still ensure good filtering performance even at a low transmission rate. In the future research, in order to further improve information transmission efficiency, we will integrate the dynamic event-triggered mechanism into the algorithm design of the PDNs set-membership state estimation. Moreover, in view of the extensive research on new energy grid connection, including wind and photovoltaic power generation, we will carry out distributed state estimation for the active PDNs combined with the algorithm proposed in this article.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

XB and XJ contributed to the conception and design of the study. MD performed the method analysis. GL wrote the first draft of the manuscript. XB, JL, and XZ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References