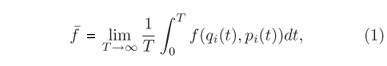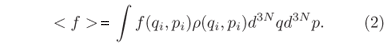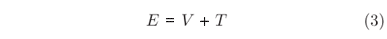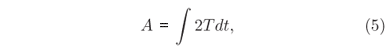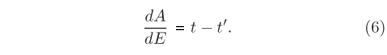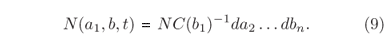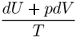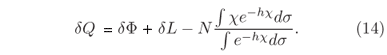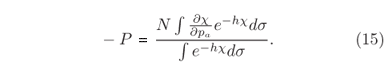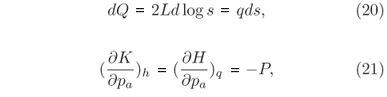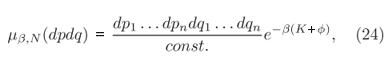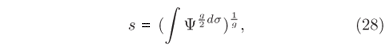Resumos

HISTÓRIA DA FÍSICA E CIÊNCIAS AFINS

A construção de uma teoria de ensembles: antecedentes em Maxwell e Boltzmann

The construction of a theory of ensemble: precedents in Maxwell and Boltzmann

Cássio C. Laranjeiras^I,1 1 E-mail: cassio@unb.br. ; José R.N. Chiappin^II,2 2 E-mail: chiappin@usp.br.

^IInstituto de Física, Universidade de Brasilia, Brasília, DF, Brasil

^IIDepartamento de Filosofia, Universidade de São Paulo, São Paulo, SP, Brasil

RESUMO

O objetivo deste artigo é investigar no trabalho de James C. Maxwell (1831-79) e Ludwig Boltzmann (1844-1906) as bases da construção daquilo que modernamente, após Willard Gibbs (1839-1903), ficou conhecido como uma teoria de ensembles, uma abordagem metodológica que alimentou a busca por uma fundamentação estatística para as leis da termodinâmica.

Palavras-chave: mecânica estatística, Ludwig Boltzmann, James Clerk Maxwell, heurística.

ABSTRACT

The purpose of this paper is to research the bases of the construction in James C. Maxwell (1831-79) and Ludwig Boltzmann's (1844-1906) work of what is now known as the theory of ensembles, after Willard Gibbs (1893-1903). It is a methodological perspective that stimulated the search for a statistical ground for the laws of thermodynamics.

Keywords: statistical mechanics, Ludwig Boltzmann, James Clerk Maxwell, heuristics.

1. Introdução

Em 1901 a mecânica estatística recebeu uma formulação abrangente através dos Princípios Elementares em Mecânica Estatística de Willard Gibbs (1839-1903). Logo no prefácio do seu trabalho, Gibbs cita Clausius, Maxwell e Boltzmann como os fundadores deste campo, cuja origem se deve ao esforço de dedução das leis da termodinâmica a partir de princípios da mecânica. Um dos aspectos mais característicos da abordagem de Gibbs, desenvolvida ao final de uma carreira essencialmente dedicada à termodinâmica, é o que pode ser chamado de sua atitude pragmática em relação à mecânica estatística, que ele vai conceber de maneira autônoma e, portanto, independente de toda e quaisquer hipóteses relacionadas a estrutura da matéria³ 3 Esta atitude pragmática de Gibbs em relação a mecânica estatística está na raiz mesma da preferência dos opositores de Boltzmann, em particular Friedrich Wilhelm Ostwald (1853-1932), pela abordagem de Gibbs. [1].

No século XIX as investigações naquilo que hoje conhecemos como mecânica estatística operavam principalmente com modelos ajustados à noção de estrutura da matéria, sendo as moléculas consideradas como indivíduos no sentido estatístico. Maxwell e Boltzmann perceberam um segundo ponto de vista e que Gibbs soube explorar, ainda que abrindo mão de hipóteses concernentes à constituição da matéria. É na percepção desse segundo ponto de vista que vamos identificar as bases da construção daquilo que modernamente, após Gibbs, ficou conhecido como uma teoria de ensembles, uma abordagem que alimentou a busca por uma fundamentação estatística para as leis gerais da termodinâmica [2].

Nesta abordagem, o estado dinâmico de um dado sistema S, S_i(i = 1,2,3¼), caracterizado pelas coordenadas generalizadas q_i e momentos generalizados p_i, é representado por um ponto G(q_i,p_i) no espaço de fase de 6N dimensões, onde N é o número total de partículas que compõem o sistema S. A evolução do estado dinâmico no tempo é representada por uma trajetória de G no espaço de fase, governada pelas equações canônicas do movimento do sistema e pela natureza dos vínculos que atuam sobre ele. A solução dessas equações como função do tempo nos permitiria a determinação de todas as grandezas termodinâmicas (observáveis do sistema), f(q_i,p_i).

No equilíbrio, todos os observáveis termodinâmicos são independentes do tempo e, portanto, em princípio, estas quantidades deveriam ser calculadas como médias temporais tomadas ao longo da trajetória de G(q_i,p_i) no espaço de fase, ou seja

onde a dependência temporal de f(q_i(t),p_i(t)) é dada pelas equações de movimento. No entanto o cálculo da média temporal ao longo da trajetória de fase exigiria a solução completa das equações de movimento, o que inviabiliza a tarefa.

Foi com o objetivo de desenvolver um formalismo mais apropriado para o cálculo das grandezas termodinâmicas que surgiram os chamados ensembles estatísticos. Ao invés de trabalharmos com um único sistema (o sistema a ser estudado) considera-se, juntamente com ele, uma infinidade de cópias fictícias, réplicas do sistema real, portanto, um ensemble de sistemas similares em sua natureza (macroestado), mas que diferem entre si nos valores particulares que seus parâmetros (coordenadas de posição e momento) assumem num dado instante (microestado). Agora, a dependência temporal da trajetória de G no espaço de fase não tem mais importância. A cada ponto deste espaço, (q_i,p_i), identificado com uma cópia do sistema real em um certo microestado, é atribuído um peso probabilístico, dado pela função r(q_i,p_i) (função densidade de probabilidade), que representa a probabilidade de que o microestado que ele representa seja atingido pelo sistema. Desta forma, um ensemble estatístico é constituído pelo conjunto dos estados microscópicos aos quais se associam determinados pesos probabilísticos. Assim, as grandezas termodinâmicas, f(q_i,p_i), seriam representadas por seus valores médios ( < f > ) em um dado macroestado, para o qual cada microestado contribuiria com um peso correspondente, r(q_i,p_i). Essa é a chamada média no ensemble de uma dada grandeza, que pode ser escrita como

Um aspecto fundamental da teoria de ensemble é a afirmação de que todas as grandezas termodinâmicas podem ser interpretadas como médias de suas correspondentes funções f(q_i,p_i), médias tomadas sobre o espaço de fase⁴ 4 A fundamentação lógica para esta interpretação caracteriza o chamado problema ergódico, cuja origem remonta a Maxwell e Boltzmann e cuja solução completa ainda se encontra em aberto. .

Ao longo deste artigo investigaremos no trabalho de James C. Maxwell (1831-79) e Ludwig Boltzmann (1844-1906) as bases dessa construção.

2. Maxwell e a noção de ensemble

Em 1879 Maxwell introduziu a noção de ensemble, uma idéia já utilizada por Boltzmann em 1871 [3], em um artigo intitulado On Boltzmann's Theorem on the Average Distribution of Energy in a System of Material Points [4], ao fazer considerações gerais sobre o equilíbrio térmico.⁵ 5 Este fato é reconhecido por Gibbs que, no prefácio de sua monografia rende importante tributo à Boltzmann, sublinhando o fato de que este último foi o primeiro a considerar explicitamente a distribuição de fase de um grande número de sistemas, assim como a estudar a evolução desta distribuição através do teorema de Liouville, conforme a Ref. [5, p. viii]. Neste momento o interesse de Maxwell estava voltado para o desenvolvimento de um novo método de cálculo da distribuição da energia em um dado sistema em equilíbrio (equipartição da energia).

Boltzmann já havia se debruçado sobre o problema na 3ª seção do seu artigo de 1868 (Estudos Sobre o Equilíbrio das Forças vivas entre os Pontos Materiais em Movimento) [6], apresentando como condição de sua dedução restrições que lançavam dúvidas sobre a generalidade da solução. Na dedução de Boltzmann, proposta para o caso em que as moléculas interagem unicamente por colisão, no estado de equilíbrio a equipartição da energia tem lugar, o que significa que a energia cinética disponível será distribuída igualmente entre os graus de liberdade do movimento. Assim, no caso de moléculas pontuais, que possuem unicamente movimento translacional, as componentes x, y e z das velocidades de todas elas terão, no equilíbrio, a mesma proporção da energia cinética total disponível.

Maxwell reconhecia a generalidade da solução de Boltzmann, não encontrando, portanto, razões para o uso da restrição relacionada a interação entre as moléculas. Desta forma ele propôs um método de cálculo para o equilíbrio onde a equipartição da energia resultante pode ser obtida de maneira independente de qualquer afirmação sobre os detalhes da interação entre as moléculas, sendo válido até mesmo no caso de interação de longo alcance por meio de um potencial. Preocupado com a existência de possíveis dúvidas em torno da generalidade da solução de Boltzmann para o problema da equipartição da energia em um sistema em equilíbrio, ele diz:

Na 3ª seção do seu artigo de 1868, sob o título Solução Geral do Problema do Equilíbrio das Forças Vivas, Boltzmann colocava como condição da dedução do teorema da equipartição da energia a interação por colisão entre as moléculas que constituem o sistema. Maxwell não encontrava razões que justificassem essa limitação. Ele afirmou:

Maxwell argumenta que uma prova direta do teorema da equipartição da energia exigiria a adoção de uma hipótese, cuja validade geral ele não reconhecia. Ele diz:

Esta pode ser considerada sua afirmação mais explícita acerca da hipótese ergódica.⁶ 6 A hipótese ergódica considera que um sistema mecânico, se deixado livre de perturbações, passará através de cada ponto do espaço de fase estando sobre uma superfície de energia. Em outras palavras, as posições e velocidades de todas as massas pontuais (representando os átomos) eventualmente tomarão cada valor possível consistente com a dada energia total do sistema De suas palavras pode-se depreender, em consonância com as afirmações de Brush [7, p. 170-171], que Maxwell propôs a hipótese ergódica unicamente para sistemas mecânicos interagindo com sua vizinhança, ao invés de sistemas mecânicos não perturbados. Ele não exige que esta interação seja de natureza aleatória em nível microscópico. Se as paredes do recipiente são rígidas, sua ação sobre as moléculas é completamente determinística, tendo como efeito golpear o sistema de uma órbita para a outra sobre a superfície de energia.⁷ 7 Brush chama-nos a atenção de que a versão da hipótese ergódica usualmente atribuída a Maxwell e a Boltzmann vai além daquilo que suas palavras nos permitem depreender.

Maxwell estava portanto diante do seguinte problema:

É justamente com vistas a resolução deste problema que Maxwell nos apresenta o instrumento heurístico a ser adotado, momento em que a noção daquilo que viria a ser conhecido como ensemble é sugerida. Vejamos as palavras de Maxwell:

O ensemble aqui apresentado por Maxwell estabelece a condição de constância da energia, o que o caracteriza, numa linguagem posteriormente adotada por Gibbs, como ensemble microcanônico.

Seu ponto de partida é o estabelecimento das condições do sistema a ser analisado:

A estratégia adotada por Maxwell na investigação do movimento, sob a base da noção de ensemble, é a seguinte:

1. Utilização da noção de ensemble na representação do sistema a ser estudado;

2. Especificação dinâmica do movimento;

Maxwell supõe o sistema material como sendo aquele de tipo mais geral, tendo sua configuração determinada por n variáveis q₁,q₂...q_n e seu movimento determinado pelos momentos correspondente p₁,p₂...p_n. Assim, o estado do sistema em qualquer instante fica completamente definido se nós conhecemos os valores destas 2n variáveis para aquele instante. A energia potencial do sistema (V) é definida como uma função das variáveis que definem a configuração do mesmo, a saber, q₁,q₂...q_n, e a energia cinética, expressa em termos dos q's e p's, é representada por T. Assim, a energia total, representada por

é uma constante durante todo o movimento do sistema. As equações de movimento para este sistema são portanto

onde q_r e p_r são a coordenada e o momento correspondentes.

3. Definição da ação do sistema durante o movimento;

A ''ação'' (A) do sistema durante o movimento é definida por Maxwell como duas vezes a integral no tempo da energia cinética, tomada do início ao fim do movimento, ou seja

e expressa em função das coordenadas iniciais (q₁'...q_n') e finais (q₁...q_n) e da energia total (E).

Ele nos mostra ainda que se t' e t são respectivamente os valores do tempo no início e no fim do movimento,

Ao longo de sua investigação, Maxwell pretende comparar o produto das diferenciais das coordenadas e momentos no início do movimento (ds'ds'dt') com o correspondente produto no fim do movimento(ds dsdt).⁸ 8 Por brevidade Maxwell escreve ds = dq 1 ... dqn para o produto das diferenciais das coordenadas, e ds = dp 1 ... dpn para o produto das diferenciais do momento.

4. Especificação estatística do sistema;

Na especificação estatística do sistema Maxwell adota uma definição mais ampla de fase. Até então ele vinha falando de uma fase (p,q) supondo-a definida pelos valores das n coordenadas e n momentos. Agora ele nos diz que o sistema está numa dada fase (a₁b) sempre que os valores das coordenadas são tais que q₁ está entre b₁ e b₁+db₁, q₂ entre b₂ e b₂+db₂, e assim por diante; Também p₂ entre a₂ e a₂+da₂, e assim por diante. Os limites da primeira componente do momento, p₁, não estão especificados porque os valores de p₁ não são independentes das outras variáveis, sendo dados em termos de E e das outras 2n-1 variáveis, em virtude da equação da energia. As quantidades a, b são do mesmo tipo que p e q respectivamente, com a diferença de que elas não variam com o movimento do sistema. Vê-se, portanto, que no método estatístico, adotado por Maxwell, o sistema não é seguido durante seu movimento. Toda atenção é fixada sobre uma fase particular, averiguando-se se o sistema está ou não naquela fase, e também quando ele entra e quando sai da mesma. Trata-se, portanto, de saber acerca da probabilidade de um dado sistema ser encontrado numa determinada fase. Contrapondo-se, então, a uma determinada concepção de probabilidade expressa por Boltzmann, Maxwell estabelece as condições para sua utilização do conceito de probabilidade. Ele nos diz:

Operando com o conceito de probabilidade acima estabelecido, ele vai buscar expressar o número de sistemas que, num dado tempo t, estão na fase (a₁b)(N(a₁,b,t)), como função do número total de sistemas (N), das coordenadas e momentos com seus limites, e o tempo t, ou seja,

sendo a forma da função f dada por

Assim, N(a₁,b,t) pode ser reescrita como

5. Definição de distribuição estacionária;

Maxwell nos diz ainda que se a distribuição dos N sistemas nas diferentes fases é tal que o número em uma dada fase não varia com o tempo, a distribuição é dita ser estacionária. O que ele procura mostrar é que se a distribuição é estacionária, uma certa função das variáveis (C) deve ser constante para todas as fases pertencentes ao mesmo caminho. Ele diz:

Como resultado de suas investigações, que de fato estabelece uma solução para o problema da distribuição estacionária, Maxwell pôde chegar a equipartição da energia, estabelecendo que a energia cinética média correspondente a qualquer uma das variáveis é a mesma para cada uma das variáveis do sistema.

Portanto, a noção de um ensemble de sistemas, uma distribuição de probabilidade sobre possíveis micro-estados para o sistema, encontra em Maxwell uma importante referência. Com ele a distribuição micro-canônica padrão como no mínimo uma distribuição invariante sob a evolução dinâmica, e a identificação dos valores de equilíbrio com as médias na fase das quantidades relativas a esta distribuição de probabilidades aparecem no cenário da discussão. Ao mesmo tempo Maxwell introduziu o que, nas palavras de Sklar [8, p. 157], se tornou o ''problema clássico da teoria de equilíbrio", a saber o de demonstrar que a distribuição de probabilidade padrão é a única estacionária no tempo.

A próxima seção procura identificar no trabalho de Boltzmann a raiz mesma da utilização dos ensembles como recurso heurístico para o cálculo das propriedades de um dado sistema.

3. Boltzmann e o papel heurístico dos ensembles

Conforme comentamos no item anterior, Boltzmann já havia utilizado em seu artigo de 1871 (Algumas Considerações Gerais Sobre o Equilíbrio Térmico) [3], portanto antes de Maxwell, a noção de ensemble como recurso heurístico ao fazer considerações de caráter geral sobre o equilíbrio térmico, buscando assim justificar as propriedades de equilíbrio dos gases. Mais especificamente, o objetivo de Boltzmann era obter uma prova de que o comportamento médio de um gás durante um movimento de duração ilimitada é idêntico ao seu comportamento no equilíbrio térmico, caracterizado pela distribuição de Maxwell-Boltzmann. Nesta direção, Boltzmann realiza o cálculo das médias temporais (que nos dão as probabilidades das diferentes distribuições) de funções que caracterizam as distribuições médias dos estados fazendo uso de um conjunto de sistemas (réplicas do gás estudado) que se movem de uma maneira completamente independente um do outro, de tal forma que todos têm a mesma energia (ensemble microcanônico). A estratégia foi calcular valores médios sobre o conjunto de sistemas (média no ensemble) igualando-os às médias temporais, que era o que lhe interessava calcular.⁹ 9 Para uma maior discussão acerca da heurística de Boltzmann, ver Ref. [9] Boltzmann achava difícil atribuir comportamento ergódico a um sistema único, o que implicava numa estrita dependência teórica às condições iniciais, razão pela qual ele elege os ensembles.

Como ponto de partida, Boltzmann nos propõe a representação de um gás composto de muitas moléculas através de um sistema de n pontos materiais:

Portanto, da mesma forma que se pode considerar cada uma das n moléculas de um gás como um sistema separado, Boltzmann tomou um número muito grande de sistemas de partículas, estabelecendo como única diferença na analogia a consideração de que

Na seqüência do seu raciocínio ele estabelece de maneira explícita a caracterização de microestados associados a um dado macroestado, completando, juntamente com as duas citações apresentadas anteriormente, aquilo que podemos chamar de sua idéia original da noção de ensemble.

Portanto, a partir da utilização desse novo recurso heurístico (ensemble microcanônico), Boltzmann pôde associar a um dado macroestado (o estado do sistema real) diferentes possíveis microestados (os estados dos diferentes sistemas de pontos), que são diferentes maneiras, de um ponto de vista microscópico, de alcançá-lo.

Em seu artigo de 1872, Novos Estudos Sobre o Equilíbrio Térmico de Moléculas Gasosas [10, p. 401], Boltzmann voltou a utilizar a noção de ensemble ao tentar encontrar uma relação apropriada entre entropia definida mecanicamente e a 2ª lei da termodinâmica.

A grande vantagem da utilização desta abordagem é que o problema, que antes estava relacionado ao acompanhamento da sucessão temporal de configurações de um dado sistema particular, agora se transferia para a determinação de como o número total de sistemas estará distribuído entre as várias configurações e velocidades possíveis em qualquer instante de tempo, quando a distribuição tiver sido dada para algum instante inicial. Foi, portanto, com o objetivo de contornar a impossibilidade prática de determinar a evolução temporal de um sistema com muitos graus de liberdade, e nela calcular os valores médios das várias grandezas termodinâmicas, que Boltzmann fez uso do método de ensembles. A análise da evolução temporal do sistema é então substituída pela análise de um ensemble estatístico de cópias fictícias do sistema real, todas compartilhando a mesma dinâmica, mas distribuídas sobre possíveis valores compatíveis com os vínculos do sistema. Numa passagem de Gastheorie, esse objetivo fica claramente explicitado:

Boltzmann retomou o tema dos ensembles em 1884¹⁰ 10 Este artigo é uma versão inicial de Boltzmann conforme a Ref. [12]. [13], desta vez ao tentar elaborar uma linha de pensamento iniciada por H. von Helmholtz (1821-1894) em 1880, com o objetivo de estudar questões fundamentais da relação entre mecânica e termodinâmica, mas apropriadamente representada pela busca por uma analogia mecânica para a 2ª lei [14]. Helmholtz havia introduzido um novo recurso heurístico, o conceito de sistemas monocíclicos,¹¹ 11 Numa linguagem moderna trata-se de sistemas cujo espaço de fase contém unicamente órbitas periódicas, ou ciclos. uma classe de sistemas mecânicos cujas equações de movimento poderiam ser escritas de uma forma tal que assemelhavam-se à segunda lei da termodinâmica. O ponto de partida de Helmholtz foi considerar um sistema mecânico, descrito pelas equações de movimento de Lagrange, cujas coordenadas generalizadas podiam ser categorizadas em duas classes distintas. As de primeiro tipo, as chamadas cíclicas, não apareciam diretamente na função lagrangiana do sistema e suas derivadas temporais, as velocidades generalizadas, apareciam na expressão da energia cinética e, portanto, nas equações de movimento. Estas velocidades, quando comparadas àquelas das outras classes de coordenadas, tornavam estas últimas desprezíveis. Os sistemas eram chamados de monocíclicos se eles tinham unicamente uma coordenada cíclica independente. Ao definir sistemas deste tipo Helmholtz tinha em mente uma clara analogia com os sistemas termodinâmicos, tais como um recipiente cheio de gás composto de muitas moléculas em rápido movimento. Neste caso as coordenadas moleculares, em qualquer instante de tempo, não tem efeito sobre as propriedades termodinâmicas do gás, embora suas velocidades moleculares determinem a energia cinética molecular, que é proporcional a temperatura. O volume do gás é um parâmetro do sistema que varia numa taxa muito lenta comparado as velocidades moleculares. As duas quantidades cuja interação constituem a essência da termodinâmica são o calor (variações na energia do sistema produzidas pelas mudanças nas velocidades moleculares) e o trabalho (produzido pela lenta variação de parâmetros do sistema como por exemplo o volume).

3.1. A noção de distribuição de probabilidade ''estacionária" sobre o espaço de fase: o conceito de Monode

Boltzmann havia percebido a importância da introdução do conceito de sistemas monocíclicos proposto por H. von Helmholtz, e foi justamente com o objetivo de refinar aquela analogia mecânica que ele escreveu o seu artigo de 1884, Über die Eigenschaften monzyklischer und anderer damit verwandter Systeme [15], agora já reforçado pela leitura do artigo de Maxwell, On Boltzmann's Theorem on the Average Distribution of Energy in a System of Material Points [4]. Logo na introdução ele afirma:

É interessante observar aqui o caráter heurístico que Boltzmann atribui aos sistemas monocíclicos de Helmholtz, percebendo-os como importantes analogias para os corpos aquecidos e não como correspondentes diretos destes últimos. Após discutir alguns exemplos (três) particulares de sistemas monocíclicos, ele chega, mais especificamente através da discussão do terceiro exemplo, a um dos momentos centrais do seu artigo, a saber, quando da introdução da noção de distribuição de probabilidade ''estacionária" sobre o espaço de fase de N partículas encerradas em um recipiente de volume V.

Ele chama o conjunto dessas probabilidades de um monode, generalizando um conceito análogo ao de sistemas monocíclicos de Helmholtz.

As órbitas de um sistema monocíclico podem ser vistas como dotadas de uma certa distribuição de probabilidade, atribuindo-se a um comprimento de arco uma certa probabilidade proporcional ao tempo gasto sobre ele pelo movimento. Um conjunto de tais comprimentos de arco forma uma coleção de distribuições de probabilidades estacionárias [16, p. 1572].

Embora o conceito de Monode tenha sido apresentado no contexto de um único sistema, Boltzmann também o utilizou no contexto de uma coleção de distribuições estacionárias (réplicas fictícias de um mesmo sistema em equilíbrio) parametrizadas diferentemente segundo a situação do sistema.

3.2. O ensemble de equilíbrio: o conceito de orthode

Uma distribuição de probabilidades estacionária, embora seja condição necessária para a representação dos sistemas em equilíbrio térmico, não é condição suficiente, razão pela qual ele vai trabalhar com a hipótese de que entre as possíveis distribuições estacionárias somente algumas podem ser intepretadas como estados de equilíbrio macroscópico. Para Boltzmann os representantes legítimos de um sistema em equilíbrio térmico deveriam obedecer a certas condições, ao se calcular os valores médios das quantidades observáveis em diferentes elementos m de um Monode, a saber:

Cumpridas estas condições o monode em questão se credenciaria como legítimo modelo mecânico da termodinâmica. Foram os monodes deste tipo que Boltzmann denominou deOrthode.

Uma vez caracterizadas as distribuições de probabilidades capazes de representar um dado sistema em equilíbrio térmico, Boltzmann passa à discussão de dois casos mais gerais (Caso 1 e 2) muito claramente especificados. Trata-se de dois tipos de orthode, momento em que são introduzidos os ensembles canônico (holode) e microcanônico (ergode), que serão analisados nas próximas duas subseções.

3.3. Introduzindo o ensemble canônico por meio do conceito de holode

Boltzmann inicia o 3^°§ do seu artigo caracterizando o sistema a ser estudado através do método de ensemble:

Operando com o método de ensemble ele introduz o ensemble canônico através da análise do que ele caracteriza como Caso 1:

dt = dr₁dr₂...dr_g. [15, p. 131-132]

As integrais são estendidas sobre todos os valores possíveis de coordenadas e momentos, sendo a totalidade de todos esses sistemas caracterizada como um holode (ensemble canônico), e cada um dos sistemas chamado um elemento do holode.

Ao apresentar a Eq. (11), Boltzmann está nos apresentando sua definição da probabilidade de se encontrar um dado sistema do holode (ensemble canônico) numa dada região do espaço de fase.

Na sequência do seu raciocínio ele escreve as expressões para as energias cinética (L) e potencial (F) do holode, respectivamente

e

sendo o valor médio de c.

O trabalho voltado para o aumento imediato do movimento interno ao sistema é escrito como

e a quantidade de movimento interno que é produzida pelo trabalho externo quando o parâmetro p_a e aumentado de dp_a, é -Pdp_a, onde

Completando sua análise ele nos apresenta outras analogias com a teoria do calor. Fazendo

ele escreve

e

Fazendo h = b = 1/KT, onde K é a constante de Boltzmann e T a temperatura absoluta, a expressão de Boltzmann (Eq. (11)) pode ser reescrita na forma

correspondendo, assim, à definição moderna de ensemble canônico. Desta forma Boltzmann estabeleceu as propriedades essenciais do ensemble canônico, mostrando que ele funciona como um modelo mecânico para a termodinâmica.

Renn chama-nos a atenção para o fato de que embora em seu Gastheorie, o único ensemble virtual considerado por Boltzmann tenha sido o ergódico, ele introduziu, ainda que no contexto de um sistema físico real, um gás, a expressão matemática do ensemble canônico, caracterizado por uma distribuição de probabilidade para os componentes atômicos [17, p. 138]. Ao tratar os gases poliatômicos Boltzmann assume que

De fato, aqui Boltzmann utiliza as coordenadas generalizadas P₁,P₂, ..., P_µ e momentos generalizados q₁,q₂,..., q_µ para representar a posição e o estado de uma molécula e não de um membro de um ensemble. h é uma constante que tem o mesmo valor para todos os tipos de moléculas; A₁ uma constante que é diferente para os diferentes tipos de moléculas; e E₁ corresponde ao valor da soma da energia cinética de uma moléculas e das energias potenciais devido as forças externas e intramoleculares que atuam sobre uma molécula num dado instante de tempo.

Embora a expressão tenha sido construída com um significado físico diferente daquele que a noção de ensemble nos proporciona, é interessante observar a correspondência, em termos analíticos, da mesma.

Já em 1871 [3] Boltzmann havia apresentado um tratamento analítico semelhante ao considerar um corpo arbitrário em equilíbrio térmico com um gás. Ali, ele nos oferece uma análise quantitativa detalhada do movimento dos átomos deste corpo, pressupondo que a energia de todo o sistema é uma constante do movimento e que as coordenadas e velocidades dos seus constituintes atômicos assumem todos os valores compatíveis com esta restrição.

3.4. Introduzindo o ensemble microcanônico por meio do conceito de Ergode

O ensemble microcanônico nos é apresentado por Boltzmann em seu artigo através da análise de um segundo exemplo (Caso 2), para o qual ele demonstra propriedades similares aquelas do ensemble canônico.

Também aqui, fazendo ds = D^1/2dp₁dp₂...dp_g Boltzmann escreve as expressões para as energias potencial e cinética do ergoden, respectivamente como

e

Analogamente ao exemplo do holode (ensemble canônico), o trabalho responsável pelo aumento da energia do sistema no ergode (ensemble microcanônico) é escrito como

Fazendo

e

dQ pode novamente ser escrito como dQ = qds.

4. Conclusão

Ao longo desse artigo discutimos o papel representado pelos trabalhos de J.C. Maxwell e Ludwig Boltzmann como antecedentes para a construção daquilo que ficou conhecido, após o trabalho de Willard Gibbs em mecânica estatística, como uma Teoria de Ensembles. Os pontos de vista defendidos por Maxwell e Boltzmann na investigação de sistemas em equilíbrio térmico lhes permitiram, particularmente a este último, o estabelecimento de métodos heurísticos para o cálculo das grandezas termodinâmicas de um dado sistema. Neste sentido, a introdução do Ensemble Canônico por meio do conceito de holode e do Ensemble Microcanônico por meio do conceito de ergode, ambos considerados por Boltzmann como ensembles ortódicos, foram aqui considerados como marcos fundamentais no trabalho de Boltzmann.

Recebido em 1/8/2007; Revisado em 14/11/2007; Aceito em 19/11/2007

Datas de Publicação

Histórico