Abstract
The Walecka model contains essentially two parameters that are associated with the Lorentz scalar (S) and vector (V) interactions. These parameters are related to a two-body interaction consisting of S and V, imposing the condition that the two-body binding energy is fixed. We have obtained a set of different values for the nuclear matter binding energies (B N) at equilibrium densities (rhoo). We investigated the existence of a linear correlation between B N and rhoo, claimed to be universal for nonrelativistic systems and usually known as the Coester line, and found an approximate linear correlation only if V - S remains constant. It is shown that the relativistic content of the model, which is related to the strength of V - S, is responsible for the shift of the Coester line to the empirical region of nuclear matter saturation.
REGULAR ARTICLES
The Coester line in relativistic mean field nuclear matter
A. DelfinoI; M. MalheiroI; V. S. TimóteoII; J. S. Sá MartinsI
IInstituto de Física, Universidade Federal Fluminense, 24210-340, Niterói, RJ, Brazil
IICentro Superior de Educação Tecnológica, Universidade Estadual de Campinas, 13484-370, Limeira, SP, Brazil
ABSTRACT
The Walecka model contains essentially two parameters that are associated with the Lorentz scalar (S) and vector (V) interactions. These parameters are related to a two-body interaction consisting of S and V, imposing the condition that the two-body binding energy is fixed. We have obtained a set of different values for the nuclear matter binding energies (BN) at equilibrium densities (ro). We investigated the existence of a linear correlation between BN and ro, claimed to be universal for nonrelativistic systems and usually known as the Coester line, and found an approximate linear correlation only if V S remains constant. It is shown that the relativistic content of the model, which is related to the strength of V S, is responsible for the shift of the Coester line to the empirical region of nuclear matter saturation.
1 Introduction
Quantum Chromodynamics (QCD) is the fundamental theory of the strong interaction and hence it should be able to explain possible modifications of hadron properties in the nuclear medium. However, typical nuclear phenomena at intermediate and low energies cannot be analitically derived from QCD, although one hopes that QCD will be solved numerically on the lattice in the near future. Meanwhile, we are left with the construction of phenomenological models in order to describe nuclear phenomena and bulk properties. On these grounds, we can conceive models in which hadrons are the degrees of freedom of some proposed Lagrangian density. From the Lagrangian, a two-nucleon interaction can be obtained and the parameters of this interaction are adjusted to reproduce the two-nucleon bound and scattering states observables. With this two-nucleon interaction, the many-body problem can be solved via a Brueckner-Hartree-Fock (BHF) calculation or a Relativistic-Brueckner-Hartree-Fock (RBHF) [1,2,3], if one intends to incorporate relativistic effects.
Another phenomenological way to treat the many-body problem has been proposed by Walecka and collaborators [4,5]. Their approach is based on a simple renormalizable field-theoretical model which is often referred to as Quantum Hadrodynamics (QHD). In this model nucleons interact through the exchange of s and w mesons, with the s providing medium range attraction and the w the short-range repulsion. This model is usually solved in the mean field approximation (MFA), in which the meson fields are replaced by their expectation values. The Walecka model has achieved important goals in the description of hadronic matter such as, for example, the calculation of some bulk properties of nuclear matter as well as some properties of finite nuclei. An interesting result of the model was to show the relativistic mechanism for nuclear matter saturation: it occurs at a density (ro) at which the scalar (S) and the vector (V) potentials largely cancel each other out. A curious aspect of this model is that the masses of the scalar and vector mesons ( ms and mw), and the coupling constants ( gs and gw) are eliminated in the equation of state for infinite nuclear matter in favour of  =
=  M2/
M2/ and
and  =
=  M2/
M2/ . These dimensionless constants,
. These dimensionless constants,  and
and  , the only free parameters in this simple version, are fitted to reproduce the nuclear matter bulk properties. Besides the relativistic mean field calculation, the Walecka model has also been used in a more complete treatment, the relativistic Hartree-Fock approximation [5,6,7]. A more sophisticated version of the Walecka model that includes non-linear self-interactions of the scalar field has been proposed by Boguta and Bodmer[8]. This non-linear version of the Walecka model has obtained not only more reasonable results for the incompressibility and the effective nucleon mass at nuclear matter saturation density but also has described various aspects of nuclear structure properties [9,10]. This model with a very limited number of parameters is also able to describe deformed nuclei [11,12] and for the first time the anomalous shifts in the isotopic chains of different nuclei has been explained [13,14]. As a consequence of all this work, a new parametrization for this non-linear version of the Walecka model has been proposed and gives a very good description not only for the properties of stable nuclei but also for the nuclei far from the valley of beta stability [15].
, the only free parameters in this simple version, are fitted to reproduce the nuclear matter bulk properties. Besides the relativistic mean field calculation, the Walecka model has also been used in a more complete treatment, the relativistic Hartree-Fock approximation [5,6,7]. A more sophisticated version of the Walecka model that includes non-linear self-interactions of the scalar field has been proposed by Boguta and Bodmer[8]. This non-linear version of the Walecka model has obtained not only more reasonable results for the incompressibility and the effective nucleon mass at nuclear matter saturation density but also has described various aspects of nuclear structure properties [9,10]. This model with a very limited number of parameters is also able to describe deformed nuclei [11,12] and for the first time the anomalous shifts in the isotopic chains of different nuclei has been explained [13,14]. As a consequence of all this work, a new parametrization for this non-linear version of the Walecka model has been proposed and gives a very good description not only for the properties of stable nuclei but also for the nuclei far from the valley of beta stability [15].
The RBHF and Walecka models treat the many-body problem in different perspectives. The RBHF approach starts from a two-nucleon interaction which, in principle, fits some of the two-nucleon observables and proceeds iterating an effective two-nucleon t-matrix up to the point where convergence is obtained to the nuclear matter saturation. Therefore, depending on the two-nucleon interaction used, the nuclear matter binding energy and the saturation density change. On the other hand, the Walecka model and some of its variants try first of all to fit directly the observed nuclear matter binding energy at the experimental density. The tracing back of the two-nucleon interaction becomes difficult in this mean field scenario. To understand why, let's point out that the two-nucleon interaction that emerges from the Walecka model in the static approximation is the sum of two Yukawa potentials, one attractive and the other repulsive. The range of these potentials should be controlled by the masses of the mesons, ms and mw. However, the mean field approach in a Hartree perspective shows a dependence only on the dimensionless constants  and
and  , as already pointed out, and we loose track of the value of ms and mw. Let us recall that, in the mean field picture, this happens in a medium where each nucleon feels equally an averaged constant interaction coming from all the other nucleons. If one intends to have a crude idea about how a mean field many-body calculation such as the Walecka model may be connected to a two-body system in the vacuum, one has to model a two-body interaction in a relativistic perspective. The simplest interaction should be the sum of two large potentials, a scalar one S and the time component of a vector one V, each of them with an absolute value of a few hundreds MeV. In infinite nuclear matter, in the framework of the Walecka model, these two components cancel each other out to a large extent in the calculation of the binding energy. The assumption is that the same mechanism applies in the two-nucleon system to calculate the two-nucleon binding energy.
, as already pointed out, and we loose track of the value of ms and mw. Let us recall that, in the mean field picture, this happens in a medium where each nucleon feels equally an averaged constant interaction coming from all the other nucleons. If one intends to have a crude idea about how a mean field many-body calculation such as the Walecka model may be connected to a two-body system in the vacuum, one has to model a two-body interaction in a relativistic perspective. The simplest interaction should be the sum of two large potentials, a scalar one S and the time component of a vector one V, each of them with an absolute value of a few hundreds MeV. In infinite nuclear matter, in the framework of the Walecka model, these two components cancel each other out to a large extent in the calculation of the binding energy. The assumption is that the same mechanism applies in the two-nucleon system to calculate the two-nucleon binding energy.
Calculations done for the nonrelativistic nuclear matter BHF model [1], performed with different two-nucleon interactions, all of them fitting the deuteron binding energy and scattering data, show a correlation between the binding energy and the corresponding saturation density. This correlation, known as the Coester line, shows that the results obtained using different nucleon-nucleon interactions predict nuclear matter saturation to be located along a line which does not include the empirical data [16]. Recent work [17] based on a relativistic model of the nucleon-nucleon interaction addresses the discussion of whether this same correlation also takes place in a relativistic many-body calculation, exhibiting thus a kind of universality. We focus on the same question and, through a simple model, find that such a correlation is indeed present when the quantity V S is approximately constant. This last assumption can be justified since results from different hadronic models suggest that, in order to reproduce the experimental spin-orbit splittings for finite nuclei, the V S quantity should lie in a narrow band [19]. Moreover we conclude that the relativity within the model, which is related to the strength of V S, is responsible for the shift of the Coester line to the empirical region of nuclear matter saturation. We see this as an indication of a Dirac structure for the N-body potential with large scalar and vector parts.
After having finished this work we became aware of the appearance of a very recent paper analyzing this same correlation with the Bonn potentials; these involve different types of meson exchanges, in a relativistic Brueckner approach [18]. Representing the in-medium on-shell T matrix covariantly by five Lorentz invariant amplitudes, this last paper also arrives at the same conclusion as ours, namely that the new Coester lines are shifted towards the empirical region of saturation supporting the Dirac structure of the Nucleus-Nucleus potential.
Thus we can see that, despite dealing with a simple two-body model that has only central terms and models nuclear matter with the simple linear version of the Walecka model, we have the right physics, which is embeded in the relativistic form of the potential with large scalar and vector parts.
2 The two-body model
We start out with a two-body interaction consisting of a repulsive part (V) and an attractive one (S). For simplicity, we will take the potentials as constant inside a determined radius Ro and zero otherwise. The relativistic interaction is given by the operator U = UR = S + gºV, where gº is the time component of the Dirac matrix and S is implicitly multiplied by the identity matrix. We simulate our two-body system by a one-body Dirac equation in spinorial form,
The above equation can be solved for U = gºS (the relativistic case where S is considered as the time component of a pure attractive vector interaction, hereafter labeled R1) or for U = UR (the relativistic case with scalar and vector interactions, R2). We have solved Eq. (1) for each of these two potentials and for zero orbital angular momentum in coordinate space for different values of Ro, varying from 1.35 to 1.7 fm, obtaining different values for the two-body binding energy B2 = E M. Since we will later establish a connection with a N-body relativistic Walecka model, we have already imposed, for the case U = UR, a constraint on S and V to satisfy the optical relationship required from the Hugenholtz-van Hove theorem for any relativistic nuclear matter model in the mean field approximation [20],
where BN is the nuclear matter binding energy per nucleon, kf the Fermi momentum at saturation density, and M the bare nucleon mass. We have identified in the relativistic model R2 the quantity S + V with the depth of the square well vector potential S. This identification comes often when one interprets the Walecka model as qualitatively performing a large cancellation between S and V, resulting in a value close to 70 MeV for S. In Fig. (1) we display our results for the case BN = 16 MeV, kf = 1.3 fm1 , Ro= 1.4 fm, and M = 939 MeV where, for the sake of comparison, a nonrelativistic Schroedinger equation calculation for the nonrelativistic interaction UNR = S is included. The curves show that the solution of the relativistic Dirac equation with the time component of a pure vector interaction changes the nonrelativistic Schroedinger result only slightly. The binding energy in the former has a value somewhat greater than in the latter. However, the Dirac equation solved with the relativistic interaction, containing scalar and vector parts, changes dramatically the two-body binding in the opposite direction, i.e. the system becomes less bound.
The results can be understood as follows. The three distinct cases can be presented through formal dispersion relation equations in terms of the large component c of the wave function,
where in the R2 model D = V S, S = S + V , and in Eqs. (7 - 8) e stands for the difference between relativistic energy and the nucleon rest mass.
The results can be understood as follows. The three distinct cases can be presented through formal dispersion relation equations in terms of the large component c of the wave function,
where in the R2 model D = V S, S = S + V , and in Eqs. (7 - 8) e stands for the difference between relativistic energy and the nucleon rest mass.
All these cases can be cast into an unified formula in terms of a nucleon effective mass M*,
where
Since S and D are negative and positive quantities respectively, Eqs. (10 - 12) suggest that the model R1 (where the effective mass is larger than M, leading to a smaller kinetic energy) should in fact lead to a more tightly bound system, with greater binding energy than model NR, whereas model R2 (where the effective mass is smaller than M, leading to a larger kinetic energy) is the case where the system is less bound. The same information could be inferred if one thinks in terms of the effective quantities S* = S(1 S/2M) and e* = e(1 S/M) for Eq. (7), and S* = S(1 D/2M) and e* = e(1 D/M) for Eq. (8). In the cases we are discussing, the binding energy is small compared to the nucleon rest mass and we have neglected terms of order e2/2M. Note that for the model R2, not only S but also D, appear in Eq. (12). The potential depth S and the radius Ro control the two-body binding energy in Eqs. (10) and (11), whereas in Eq. (12) an additional value - D - is needed, working therefore as a new degree of freedom of the problem, since for the same Ro, different possible values of S and D are possible, as shown in Fig. 2. The large difference between the results of the models R1 and R2 is not surprising, since D is expected to be about ten times larger than S. To stress this point, it is worth mentioning that the two-body bound state for the R1 model arises when - S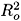 > p2
> p2
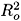 > p22/8, in units where c = 1.
> p22/8, in units where c = 1.
3 The N-body model
The N-body model we use for nuclear matter is the linear Walecka model that now we briefly present. The degrees of freedom are baryon fields (y), scalar meson fields (s), and vector meson fields (w). The Lagrangian density is given by
where Fmn = ¶mwn ¶nwm, M is the bare nucleon mass, and ms and mv are the scalar and vector mesonic masses respectively. From the above Lagrangian we obtain, through the Euler-Lagrange formalism, the equations of motion for the nucleon and mesons fields.
When the meson fields are replaced by the constant classical fields so and wo, we arrive at the mean-field approximation with the equations
where rb and rs are the vector and scalar densities respectively.
Now we define the scalar (S) and the vector (V) potentials. This can be done by looking at the Dirac equation for the models, and rewriting M* in the form M* = M gss = M + S. Still from the analysis of the Dirac equation, V can be defined as a quantity which shifts the energy, V = gvwo. It is convenient to introduce the following dimensionless quantities: m* = M*/M,  =
=  M2/
M2/ , and
, and  =
=  M2/
M2/ . Using Eqs. (14) and (15) we can rewrite the scalar and vector potentials in terms of
. Using Eqs. (14) and (15) we can rewrite the scalar and vector potentials in terms of  and
and  as
as
The expressions for the energy density and pressure at zero temperature can be found as usual by the average of the energy-momentum tensor,
and
where rB = (g/6p2) , g = 4 is the degeneracy factor for symmetric nuclear matter, and E*(k) = (k2 +
, g = 4 is the degeneracy factor for symmetric nuclear matter, and E*(k) = (k2 +  )1/2.
)1/2.
The solution of the model is obtained explicitly through the minimization of  as a function of m*. The equation thus obtained reads
as a function of m*. The equation thus obtained reads
where we have introduced the dimensionless variable x =  . This equation has to be solved self consistently and provides the basis for obtaining all kinds of thermodynamical quantities in the mean field approach we are using.
. This equation has to be solved self consistently and provides the basis for obtaining all kinds of thermodynamical quantities in the mean field approach we are using.
The usual procedure to obtain the values of the coupling constants is the following: at the saturation density ro the pressure vanishes ( hydrostatic equilibrium ) and at this same point the Hugenholtz-van Hove theorem allows us to write down the relation, already built-in in Eq.(2),  /ro = V + [
/ro = V + [ + (M + S)2]1/2 M. These two constraints can then be used to find the constants
+ (M + S)2]1/2 M. These two constraints can then be used to find the constants  and
and  by imposing the experimental values for the nuclear matter binding energy
by imposing the experimental values for the nuclear matter binding energy  /ro M = BN = 16 MeV and for the density ro = 0.15 fm3.
/ro M = BN = 16 MeV and for the density ro = 0.15 fm3.
We could have used the non-linear version of the Walecka model discussed in the introduction [15]. This would have changed the expression for the energy density and the self consistent Eq.(19); however, the correlation we are analyzing in this work would still survive, because of the presence of the large scalar and vector potentials.
4 Results and discussions
To look for the correlation between two-body and N-body bindings we proceed in the following way. From the two-body calculation for a fixed two-body binding energy B2 at a given radius Ro one obtains the scalar (S) and the vector (V) potentials. In the Walecka model we then use these two quantities, coming from the two-body calculation, in order to find the constants  and
and  . Only after we have these constants do we proceed in the calculation of the N-body system saturation. Therefore, we will have a set of saturated (BN,ro) pairs for each different (S, V) set pairs, which keeps a fixed B2. We have chosen a fixed B2 = 2 MeV, allowing variation of Ro from 1.4 fm to 2.1 fm. The set of (Ro,S,V) is given by Fig. 2 in a three-dimensional plot.
. Only after we have these constants do we proceed in the calculation of the N-body system saturation. Therefore, we will have a set of saturated (BN,ro) pairs for each different (S, V) set pairs, which keeps a fixed B2. We have chosen a fixed B2 = 2 MeV, allowing variation of Ro from 1.4 fm to 2.1 fm. The set of (Ro,S,V) is given by Fig. 2 in a three-dimensional plot.
Within the above procedure we have obtained the set of (BN,ro) values presented in Fig. 3. In principle, there is no clear correlation between BN and ro unless one constrains the interaction of the two-body system to have the same range Ro but allowing different values of D, or to have the same value of D but having different Ro values. In the first case, the correlation points show a positive slope for increasing saturation density while in the second one, the Coester line correlation is present. This correlation has been shown to exist in nonrelativistic calculations of the nuclear matter saturation point. Different phenomenological two-body potentials furnish different (BN,ro) values, which lead to a rough linear increasing of BN for increasing ro also shown in the Fig.3. To trace back the reason why this happens in the relativistic case, we have rewritten Eq. (2) as
where M* = M(1  ). Since BN
). Since BN  D, M* ® M(1 D/2M) and when D becomes constant, Eq. (20) acquires a nonrelativistic form with an effective nucleon mass. The relativistic information of the model is contained in the strenght of D. The relativistic effect is shown in Fig. 3, where the Coester line is shifted to the empirical region of saturation provided D is large. This suggests a Dirac structure for the potential with large scalar and vector parts.
D, M* ® M(1 D/2M) and when D becomes constant, Eq. (20) acquires a nonrelativistic form with an effective nucleon mass. The relativistic information of the model is contained in the strenght of D. The relativistic effect is shown in Fig. 3, where the Coester line is shifted to the empirical region of saturation provided D is large. This suggests a Dirac structure for the potential with large scalar and vector parts.
Regarding the role of D in the nuclear data fittings, it is interesting to point out that recent nuclear matter analysis with many different quantum-hadrodynamics models show a correlation between the finite nuclei spin-orbit energy splitting and the nuclear matter effective nucleon mass m* [19]. The spin-orbit energy splitting increases as m* decreases. To accurately reproduce the empirical splittings, it is found that one should require m* to be between 0.58 and 0.64. From the Hugenholtz-van Hove theorem [20], we can relate m* and D through D = 2M BN M* ( +
+  )1/2. Therefore, a correlation between the splittings and D also exists, namely the energy splitting increases with D. Moreover, the phenomenology of finite nuclei restricts the values of D to lie in a narrow band if one intends to reproduce good results for spin-orbit splitting. On the other hand, relativistic results, obtained via Dirac-Brueckner-Hartree-Fock calculations, using three different versions (A, B and C) of the Bonn potential, show a roughly linear BN × ro correlation [1]. The corresponding nuclear matter D quantities lie on a narrow range.
)1/2. Therefore, a correlation between the splittings and D also exists, namely the energy splitting increases with D. Moreover, the phenomenology of finite nuclei restricts the values of D to lie in a narrow band if one intends to reproduce good results for spin-orbit splitting. On the other hand, relativistic results, obtained via Dirac-Brueckner-Hartree-Fock calculations, using three different versions (A, B and C) of the Bonn potential, show a roughly linear BN × ro correlation [1]. The corresponding nuclear matter D quantities lie on a narrow range.
In Fig. 4 we present the incompressibility (K) as a function of ro. Again, the possible correlations follow the same trend established in Fig. (3). Roughly, K increases linearly with ro for fixed D values. When we consider bigger values for D, K increases, turning the equation of state stiffer. In Fig. (5), the effective nucleon mass M* is displayed as a function of ro, also showing the same qualitative behavior for the possible correlations in terms of the two-body Ro and D inputs. As expected by our previous discussion, when D increases M* decreases. In these two last figures we only want to exhibit the correlations between the incompressibility and the effective nucleon mass on one hand and the saturation density on the other. The specific values of the two first quantities are not important here and we would certainly get more reasonable results for them at the nuclear matter saturation density had we used the non-linear Walecka model [15].
5 Conclusions
The plots of the binding energy versus the saturation density of nuclear matter that are obtained by nonrelativistic calculations with a large number of different two-nucleon interactions show a correlation that is known as the Coester line. In a nonrelativistic approach, the Coester line has to be conceived from the phenomenology contained in two-body systems with a low fixed binding energy interacting via a short range potential. In terms of our simple two-body model, the main ingredients are S ( the depth of the potential) and the range Ro. Both suffice to parametrize in a nonrelativistic approach the two-body problem itself, with a fixed two-body binding energy.
From a relativistic point of view, we have presented a discussion about this possible correlation. Our main conclusions can be summarized as follows:
(1) In the relativistic case with scalar and vector interactions, a new degree of freedom D arises and we have seen that unless D is constant, the correlation contained in the nonrelativistic Coester line is destroyed.
(2) Since the phenomenology of relativistic finite nuclei calculations restricts the values of D to lie in a narrow band, if one intends to reproduce good results for spin-orbit splitting, we conjecture that a Coester line would survive in such models.
(3) For large values of D we show that the relativistic Coester line is shifted to the empirical region of saturation, which we see as an indication of a Dirac structure for the potential with large scalar and vector parts, and also as a signature of the relativistic content of nuclear matter.
(4) For a fixed value of B2, the study of BN,K and M* as a function of ro suggests that they are themselves correlated.
We have modeled our system in a very simple way, where the two-body interaction has only the central term. We are aware that the phenomenological two-nucleon interactions in vacuum, as used by Reid, Paris, Hamada-Jonston, Bonn and others have not only simple central terms, but include spin-spin, spin-orbit and tensor force. Their magnitudes are different in strength. In particular, the tensor force is believed to be important for the nuclear matter saturation [21]. However, as already mentioned in our introduction, a recent paper has analyzed the Coester line for various Bonn potentials in a relativistic Brueckner approach [18]. Its conclusion is that the new Coester lines are shifted towards the empirical region of saturation, supporting a Dirac structure for the Nucleus-Nucleus potential. Then we can conclude that even when we are dealing with a simple two-body model that has only central terms, we have the dominant aspect of the correct physics. This physics is in fact embedded in the relativistic form of the potential, with scalar and vector parts, because, in the medium, many pieces of the interaction are averaged out, while the remaining part is largely dominated by the scalar and the vector central potentials [22].
To finish, we remark that for the first time a connection between the Coster line has been proposed as a function of the D = V S quantity (see Fig. 3). We have exagerated the D interval in this figure to better exhibit how the relativistic content of the model would manifest itself in the Coester lines themselves.
Acknowledgements
We would like to thank Dr. Yuki Nogami for the careful reading of our manuscript and his very useful sugestions.
References
[1] R. Brockman and R. Machleidt, Phys. Rev. C 42, 1965 (1990); ibid, Phys.Rev. C 42, 1981 (1990).
[2] B. ter Haar and R. Malfliet, Phys. Rep. 149, 207 (1987).
[3] L. Sehn, C. Fuchs, and A. Faessler, Phys. Rev. C 56, 216 (1997).
[4] J. D. Walecka, Ann. Phys. 83 (1974) 491; S. A. Chin and J. D. Walecka, Phys. Lett. B 52, 24 (1974).
[5] B. D. Serot and J. D. Walecka, Adv. Nucl. Phys. 16, 1 (1985); ibid, Int. J. Mod. Phys. E 6, 515 (1997).
[6] C. J. Horowitz and B. D. Serot, Nucl. Phys. A 399, 529 (1983) ; T. Matsui and B. D. Serot, Ann. Phys. 144, 107 (1982) ; G. Krein, D. P. Menezes, and M. Nielsen, Phys. Lett. B 294, 7 (1992).
[7] A. Bouyssy, J. -F. Mathiot, N. V. Giai, and S. Marcos, Phys. Rev. C 36, 380 (1987).
[8] J. Boguta and A. R. Bodmer, Nucl. Phys. A 292, 413 (1977).
[9] P. G. Reinhard, Rep. Prog. Phys. 52, 439 (1989).
[10] P. G. Reinhard, M. Rufa, J. Maruhn, W. Greiner, and J. Friedrich, Z. Phys. A 323, 13 (1986).
[11] Y. K. Gambir, P. Ring, and A. Thimet, Ann. Phys. 198, 132 (1990).
[12] P. Ring, Prog. Part. Nucl. Phys. 37, 193 (1996).
[13] G. A. Lalazissis and M. M. Sharma, Nucl. Phys. A 586 , 201(1995).
[14] G. A. Lalazissis, M. M. Sharma, and P. Ring, Nucl. Phys. A 597, 35 (1996).
[15] G. A. Lalazissis, J. Konig, and P. Ring, Phys. Rev. C 55, 540 (1997).
[16] F. Coester, S. Cohen, B. D. Day, and C. M. Vincent, Phys. Rev. C 1, 769 (1970).
[17] A. Amorim and J. A. Tjon, Phys. Rev. Lett. 68, 772 (1992); M. K. Banerjee and J. A. Tjon, Phys.Rev. C 56, 497 (1997).
[18] T. Gross-Boelting, C. Fuchs, and A. Faessler, nucl-th/9812002, submitted to Prog. Part. Nucl. Phys.
[19] R. J. Furnstahl, J. J. Rusnak, and B. D. Serot, Nucl. Phys. A 632, 607 (1998).
[20] N. M. Hugenholtz and L. Van Hove, Physica (Amsterdam) 24, 363 (1958).
[21] M. K. Banerjee and J. A. Tjon, Phys. Rev. C 56, 2945 (1997).
[22] P. Bernardos, V. N. Fomenko, N. V. Giai, M. L. Quelle, S. Marcos, R. Niembro, and L. N. Savushkin, Phys. Rev. C 48, 2665 (1993).
Received on 8 December, 2004
- [1] R. Brockman and R. Machleidt, Phys. Rev. C 42, 1965 (1990); ibid, Phys.Rev. C 42, 1981 (1990).
- [2] B. ter Haar and R. Malfliet, Phys. Rep. 149, 207 (1987).
- [3] L. Sehn, C. Fuchs, and A. Faessler, Phys. Rev. C 56, 216 (1997).
- [4] J. D. Walecka, Ann. Phys. 83 (1974) 491;
- S. A. Chin and J. D. Walecka, Phys. Lett. B 52, 24 (1974).
- [5] B. D. Serot and J. D. Walecka, Adv. Nucl. Phys. 16, 1 (1985);
- ibid, Int. J. Mod. Phys. E 6, 515 (1997).
- [6] C. J. Horowitz and B. D. Serot, Nucl. Phys. A 399, 529 (1983) ;
- T. Matsui and B. D. Serot, Ann. Phys. 144, 107 (1982) ;
- G. Krein, D. P. Menezes, and M. Nielsen, Phys. Lett. B 294, 7 (1992).
- [7] A. Bouyssy, J. -F. Mathiot, N. V. Giai, and S. Marcos, Phys. Rev. C 36, 380 (1987).
- [8] J. Boguta and A. R. Bodmer, Nucl. Phys. A 292, 413 (1977).
- [9] P. G. Reinhard, Rep. Prog. Phys. 52, 439 (1989).
- [10] P. G. Reinhard, M. Rufa, J. Maruhn, W. Greiner, and J. Friedrich, Z. Phys. A 323, 13 (1986).
- [11] Y. K. Gambir, P. Ring, and A. Thimet, Ann. Phys. 198, 132 (1990).
- [12] P. Ring, Prog. Part. Nucl. Phys. 37, 193 (1996).
- [13] G. A. Lalazissis and M. M. Sharma, Nucl. Phys. A 586 , 201(1995).
- [14] G. A. Lalazissis, M. M. Sharma, and P. Ring, Nucl. Phys. A 597, 35 (1996).
- [15] G. A. Lalazissis, J. Konig, and P. Ring, Phys. Rev. C 55, 540 (1997).
- [16] F. Coester, S. Cohen, B. D. Day, and C. M. Vincent, Phys. Rev. C 1, 769 (1970).
- [17] A. Amorim and J. A. Tjon, Phys. Rev. Lett. 68, 772 (1992);
- M. K. Banerjee and J. A. Tjon, Phys.Rev. C 56, 497 (1997).
- [19] R. J. Furnstahl, J. J. Rusnak, and B. D. Serot, Nucl. Phys. A 632, 607 (1998).
- [20] N. M. Hugenholtz and L. Van Hove, Physica (Amsterdam) 24, 363 (1958).
- [21] M. K. Banerjee and J. A. Tjon, Phys. Rev. C 56, 2945 (1997).
- [22] P. Bernardos, V. N. Fomenko, N. V. Giai, M. L. Quelle, S. Marcos, R. Niembro, and L. N. Savushkin, Phys. Rev. C 48, 2665 (1993).
Publication Dates
-
Publication in this collection
03 May 2005 -
Date of issue
Mar 2005
History
-
Received
08 Dec 2004 -
Accepted
08 Dec 2004




















