1. 介绍
水库大坝在防洪、供水、发电等方面发挥了巨大的作用,是水利工程体系中的重要组成部分。但是如果大坝因各种因素被损毁,那后果一般都是灾难性的。而超标准的洪水就是大坝溃决的自然因素之一。洪水是最频繁发生的自然灾害,影响了众多的人口和农田,而且还会造成人员伤亡和基础设施损坏。由于城市化,降雨时间延长和河流容量不足引起的径流率增加是洪水发生的一些主要原因。2020年入汛以后,中国南方地区发生多轮强降雨过程,造成多地发生较重洪涝灾害。截至7月9日,洪涝灾害造成27省(区、市) 3020万人次受灾,直接经济损失617.9亿元。2021年,河南山西等地也遭受了特大暴雨的袭击。所以了解流道中水流的行为对于早期洪水灾难管理和挽救生命至关重要 [1]。本文的研究方向就是通过对地表水流的数值模拟来研究洪水的行为,并对模拟过程进行并行处理和可视化。
数学模型是运用数理逻辑方法和数学语言建构的科学或工程模型,以解决各种各样的实际问题 [2]。在水利科学中,就经常使用数学模型对不同现象的流体进行模拟,使用数值方法对流体模型进行控制。我们研究使用的是洪水波传播动力学方程,最早由圣维南提出 [3],所以也被称为Saint-Venant (SV)方程。它由反映质量守恒定律的连续方程和反映动量守恒定律的运动方程组成,广泛用于预测地表流动参数,例如速度,深度或高度。SV方程是针对一维的,对于二维的地表水流,SV方程源自Navier-Stokes方程 [4],通常被称作浅水方程 [5]。由于圣维南方程组在数学上属于拟线性双曲型偏微分方程组,很难用解析方法求得圣维南方程组的解析解。因此人们提出了不同的数值方法来进行地表水流的模拟。
在计算机出现之前,就有人通过数值模拟对圣维南方程进行求解,Reinaldo和Rene [6] 较早地使用了基于显式MacCormack时间分裂格式,建立了求解二维SV方程组的数学模型,最后介绍了当时的两个工业应用,证明了模型的有效性。之后Fiedler和Ramirez [7] 也使用该方法模拟了具有空间可变性质的不连续二维水动力地表流动方程(二维圣维南方程的变体)。该方法被开发用于模拟空间可变渗透和微地形,也可用于模拟灌溉、潮滩和湿地循环以及洪水。之后随着计算机的发展,计算性能的提升 [8],越来越多的人将原本使用纸笔的模拟过程放到计算机上实现。比如Kamboh [5] 等人也是为了预测和模拟洪水行为,使用二维圣维南偏微分方程建立了具有初始条件和边界条件的数学模型。接下来,使用常见的显式有限差分法将相应模型离散化并在MATLAB上实现。最终生成的图形结构可以直观地看到随时间变化的各参数变化情况。Asier [9] 等人同样是使用二维圣维南方程来模拟降水或径流事件,使用的方法却是有限体积法,按照以下三种编程方法进行了开发和比较:顺序、多线程和众核架构。多线程代码是使用OpenMP库编写的,而众核架构是使用CUDA编写的。
综上所述,虽然很多不同的系统已经针对SV方程进行建模,并且还有了并行化、性能优化的讨论,但是还很少有对大规模圣维南系统的研究。因此本研究旨在建立一个二维的简单的有限差分模型,并使用MPI + OpenMP进行大规模处理。
2. 系统介绍
2.1. 控制方程
二维圣维南方程有很多不同的形式,因为我们并不是研究不同条件下圣维南方程不同的表示,所以只是使用了一个较为常见和简单的针对明渠的表示形式,公式如下所示,
(1)
(2)
(3)
方程1是由质量守恒得来,方程2和3分别来自x,y两个方向上的动量守恒。其中,z是指的明渠水流的海拔(深度或高度),u、v分别是在x,y两个方向上的水的流速,t是时间,g是重力加速度,S0和Sf是指水面梯度和摩擦阻力,下标中的x,y也同样表示不同方向。为了在计算机中更方便的使用这个方程组,我们需要使用微分的乘积法则对公式(1) (2) (3)进行变形,之后使用显示有限差分格式进行离散化,其中时间和空间导数分别由以下表达式离散化:
时间和空导数都是使用中心差分格式,其中时间上的中心差分也被称为跳蛙格式,它的优点是可以加强计算的稳定性。这样离散化后的等式就变成下列这种形式,
(4)
(5)
(6)
这样在简单的移项、去分母后,就可以迭代求解z、u、v三个变量。如图1所示,每次计算一个迭代值的时候都要使用到上两次迭代的结果,这也是跳蛙格式的特性。也正因如此,加强了计算过程的稳定性。

Figure 1. Schematic diagram of iterative process
图1. 迭代过程示意图
2.2. 初始条件
考虑到先将并行逻辑完整讲述,再进行规模扩大,我们采用如图2一样的长方体水槽来模拟单一明渠内流体的流动行为。

Figure 2. Schematic diagram of single open channel
图2. 单个明渠示意图
最初,我们让整个区域处于静止状态,即z = 10 m,u = 0 m/s,v = 0 m/s,然后使用公式
在明渠的中心点产生高度为1 m的洪水波。这个公式中,a0和b0分别是泛洪波最高处在x方向y方向上的定位,k是最初始的水波高度。至于a和b则是每个网格节点在坐标轴上的坐标。在我们的例子中,我们假设在区域中心产生洪水波,并且还考虑了ghost cell,因此测试值取为a = 100,b = 500,k = 10。
除上述变量外,还有一些在这里展示,Δx和Δy均为1 m,Δt = 0.01 s,且S0x = 0,Sfx= 0.1,S0y = 0,Sfy = 0.1。还有我们不考虑复杂的边界条件,选择使用自反射边界条件。
2.3. 并行策略
如同2.2提到的同样的原因,我们先选择使用四个节点进行小规模并行化。我们使用MPI对每个节点进行操作。这样,我们把200 * 1000大小的网格划分为四个大小同样为100 * 500的小网格,每个节点拥有一个自定义结构体存储每一次迭代每一个网格节点内z,u,v的值。我们使用OpenMP中#pragma omp parallel for对单次迭代中的结构为双层循环的计算部分进行并行化,对计算结束后的两个结构为单层循环的边界处理也进行同样处理。因为图1所展示的计算过程,使得在计算小网格边界值时需要使用相邻网格的边界值,所以我们使用MPI_Sendrecv()函数进行节点之间的数据交换。在数据交换结束后,一次迭代才算作完成。通过图3、图4可以更直观地理解这一并行处理。
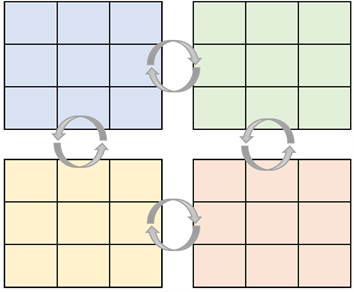
Figure 3. Schematic diagram of grid data exchange
图3. 网格数据交换示意图
2.4. 结果
我们将每次迭代每个网格节点的z,u,v值全部输出到逗号分隔值文件中,再对文件进行处理并可视化,就能很直观的看到实验结果。图5所展示的就是在不同迭代次数下模拟的二维SV方程的海拔,通过它能够清楚看出随时间变化水面高度变化的情况。图中第一个曲面所展示的是开始迭代之前的状态,经过迭代计算不断地变换成后续的状态。同样的我们也可以去分析u,v的图像,但因其看起来不够直观,在此不予展示。
3. 大规模与性能分析
我们的并行框架在设计之初就是为了大规模模拟而设计的,只需要简单更改初始条件和节点规模,规模就可以不断扩大。通过宏定义,节点内的计算规模、节点逻辑上的排列方式、节点间通信地址的寻址方式都是可以随时更改的,所以我们可以很轻易的将我们模型的规模不断扩大。

Figure 5. Simulation of water surface height of open channel
图5. 明渠水面高度模拟
接下来就是对大规模扩展进行测试,我们所有测试都是运行在国家超级计算昆山中心的共享超级计算平台。本计算集群每个节点配置1颗32核心2.5 GHz主频的x86处理器和8根16 GB DDR4 2666 ECC REG内存,采用全线速、无阻塞的200 Gb HDR Infiniband专用计算网络。而MPI是用hpcx-2.4.1编译的,OpenMP启用的线程数是32个。初始化过程和最终输出过程虽然做了多进程并行优化,但不计入执行时间。我们在大规模方面进行了强弱扩展测试。首先是弱扩展测试,在保持每个进程分配的计算量基本一致的情况下,通过不断增加进程数来测试程序的并行性能,图6是弱扩展测试的折线图,图7是对应的并行效率;之后是强扩展测试,在保证问题计算规模一定的情况下,测试程序随着核数增多单个节点计算量降低而导致程序性能的变化情况,如图8所示。此处性能的计算公式为:
式中:p为CPU数,即节点数,T1为串行执行算法的执行时间,Tp为p个处理器时并行算法的执行时间。
我们强弱扩展测试均以单核时间为基准,每种情况测试10次取均值,迭代次数为1000次。弱扩展测试的并行效率在千核时还保持在80%,框架始终运行在较高的效率之上,展性较好。强展性测试也有较为理想的并行效率,在千核内同样保持80%效率,说明划分平衡度较好。
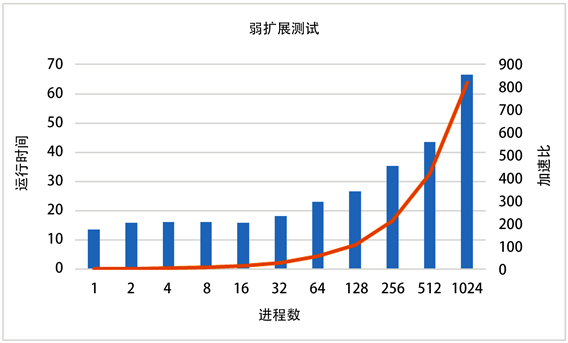
Figure 6. Weak expansion time and acceleration ratio
图6. 弱扩展测试时间与加速比
4. 总结
本文使用数值方法来模拟明渠中的二维圣维南系统。使用Leapfrog方案的有限差分法求解方程。考虑到大规模并行化要求,考虑了一个简单的长方体明渠,在中心产生洪水波。通过对z,u,v值的迭代计算输出,得到可视化图形,增强人们对洪水波的认知。然后使用MPI + OpenMP对程序进行并行化,分析并行效率。最后得出结论,所研究的并行框架具有良好的稳定性和可扩展性。