Statistical Physics-Based Model of Solid Electrolyte Interphase Growth in Lithium Ion Batteries

In our model, the electrodes are assumed to consist of random distributions of active particles. Particles at both electrodes are connected by inert binders. Further assumptions are that (1) the concentrations of solvent and Li ions in the solution phase are uniform, (2) the solution phase potential is uniform, (3) the electric potential in the solid phase of active particles is uniform; and (4) the faradaic current is distributed uniformly on the particle surfaces. Given these assumptions, particles charge and discharge uniformly throughout the electrode at all C-rates. The possibility of non-uniform current distribution or a particle-by-particle charging mechanism as discussed by Li et al.³⁵ will be considered in a forthcoming work.

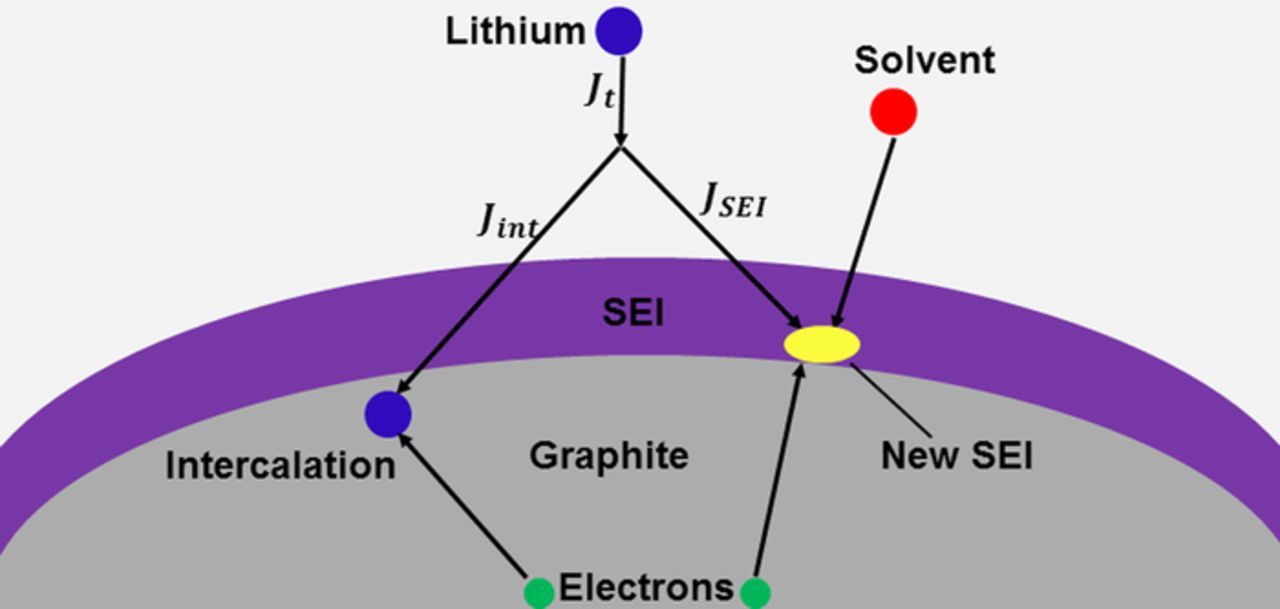
The transport of solvent molecules inside the SEI layer proceeds via diffusion, as shown in Fig. 1. The material balance for the solvent concentration inside of the SEI layer is

The boundary conditions for this equation are

and

where D_s is the diffusion coefficient for solvent molecules in the SEI layer and C_{s, b} is the solvent bulk concentration.

Zoom In Zoom Out Reset image size

The diffusion of lithium ions in an active solid particle is governed by Fick's second law in spherical coordinates,

where C denotes the concentration of lithium ions in the particle, D_i is the diffusion coefficient of Li ions in the solid and r is the radial coordinate. The boundary conditions are

For the sake of simplicity, we assume that the SEI layer grows in a reaction between Li ions, electrons and solvent molecules,

where Solv represents a solvent molecule such as ethylene carbonate, dimethyl carbonate, or diethyl carbonate and P stands for the reaction product.

The evolution of the SEI thickness is described by the Faraday law,

The SEI growth reaction is assumed to be irreversible and to follow a Tafel kinetics,

In this equation, k_SEI is the reaction rate constant for SEI growth, C_s is the solvent concentration at the particle surface and α is the electronic charge transfer coefficient. The overpotential of SEI growth is

In Eq. 10, φ_M and φ_E are the potentials in metal phase and solution phase, respectively, and κ_SEI is the ionic conductivity of the SEI. U^ref_SEI is the equilibrium potential for the SEI growth, for which a value of 0.4 V vs. Li electrode has been reported.¹⁷ J_t in Eq. 10 is the total current density,

The electrochemical reaction for intercalation/deintercalation of Li ions at the solid/solution interface can be written as

where θ_s represents a vacant site on the particle surface.¹⁸ The rate of this reaction is given by the Butler-Volmer Equation 16,

where is the intercalation reaction rate constant, C_max the maximum solid phase concentration, C_surf the Li ion concentration at the surface of active particles and C_e the concentration of Li ions in the electrolyte, which is assumed to be constant. The overpotential for the intercalation reaction at the negative electrode, η^N_int, is given by

Here, U^N is the open circuit voltage of the negative electrode, which was extracted from experimental data of Liu et al.³⁶ by Pinson et al.³⁷

In this work, we employ a population balance model (PBM) based on the Fokker-Planck Equation. This approach provides a predictive framework to explore the structural evolution of a statistical distribution of solid particles, droplets, or bubbles.³⁸ Within this framework, a random distribution of objects propagates according to the kinetics of processes that transform the properties of individual objects. The rate of these transformations of objects depends on local conditions inside the medium.³⁹ Examples for systems described successfully by this formalism include catalyst layers of PEM fuel cells, in which the catalyst particle radius distribution changes as a result of degradation,^29–32,40 biological cells in biomedical systems, e.g. in cancer research,⁴¹ or monomer droplets during suspension polymerization of vinyl chloride.⁴²

In the mathematical formalism, the electrode is represented by a particle density distribution, which is the particle number per unit volume of the electrode in the parameter space spanned by the vector variable . The temporal evolution of is governed by the FPE,⁴³

where represents a set of quantities that describe the state of individual particles in the distribution, including for instance particle radius, SEI thickness or charging state. The drift term accounts for the continuous transformation of these particle properties. Source/sink terms, included in , represent processes that delete or add particles from or to the distribution.

The present work specifically focuses on the growth of the SEI layer thickness as the structure transforming process at the single particle level. We therefore replace by the SEI layer thickness, δ. Moreover, it is assumed that the total number of particles is constant, which implies that source/sink terms are neglected. With these assumptions, we obtain a simplified FPE,

where represents the SEI thickness change. Given an initial function f(δ, 0), Eq. 16 allows the propagation of the SEI thickness and of dependent properties to be computed. The accuracy of the calculation depends on the knowledge of f(δ, 0) and on the inclusion and suitable parameterization of particle-level processes. We consider f(δ, 0) as the distribution of the SEI thickness formed during the production of the battery; this distribution depends on the fabrication approach and conditions as well as the conditioning parameters of the battery. For the present work, we determined the initial distribution using data from SEM image analysis of a LIB negative electrode, reported in Ref. 11. These data were interpolated by an exponentially modified Gaussian (EMG) function, given by

with h = 0.9, μ = 32.0, σ = 8.0 and ρ = 7.5 obtained from fitting.

The solution of Eq. 16 allows for the calculation of transiently changing moments of the distribution, viz. average SEI thickness, , and capacity fade, Q_loss, as given by

where M_SEI and ρ_SEI are the molar mass and the density of the SEI film and Q₀ is the initial capacity of the battery.

The system of equations is solved in MATLAB, using a central difference discretization scheme to transform the PDEs into a system of ordinary differential equations (ODEs). All ODEs are solved simultaneously employing the ode15s solver in MATLAB, which is a variable-step, variable-order solver based on the numerical differentiation formulae of order 5. Discretization of the PDEs is explained in the Appendix. Instead of time, we consider the number of cycles, N, as the independent transient variable, considering kinetic model parameters as effective parameters, i.e. average values over a single cycle.

The model was compared to capacity fade data from Wang et al. for varying T and charging rate. We adopted the same method for the capacity fade calculation as Wang et al.,⁴⁴ i.e., the capacity measured during the first cycle is used as Q₀. For the capacity fade simulations at different temperatures, a fitting procedure was implemented in MATLAB to find k_SEI and D_Solv for one set of operating conditions (15°C and C/2). A charging rate of 1C corresponds to a current of 2 A.⁴⁴ At the other two temperatures (45°C and 60°C), only k_SEI was fitted. For the simulation of capacity fade at different charging rates, the fitting procedure was used to obtain k_SEI and D_s at 20°C and 2C. At the other two charging rates (6C, 10C), only k_SEI was fitted. The list of parameters used in the simulations is presented in Table I. Parameters are based on the experimental work of Wang et al.⁴⁴ and they were extracted by Prada et al.⁴⁸

Table I. Model parameters used in the simulations,

Parameter	Symbol	Value	Unit	Ref.
Faraday Constant	F	96485.33	As/mol
Charge transfer coefficient	β	0.5		assumed
SEI reaction charge transfer coefficient	α	0.5		assumed
Universal gas constant	R	8.314	J/(molK)
SEI layer electric conductivity	κSEI	17.5 × 10− 5	S/m	48
SEI layer molar mass	MSEI	0.162	kg/mol	48
SEI layer density	ρSEI	1690	kg/m3	48
Intercalation reaction rate constant		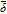2 × 10− 6	mol4 − 3βs− 1m1 − β	48
Maximum solid phase concentration	Cmax	30555	mol/m3	48
Electrolyte concentration in solution phase	Ce	1200	mol/m3	48
Active material volume fraction	εs	0.56		48
Particle radius	R	5 × 10− 6	m	48
Solvent diffusion coefficient	Ds	1.80 × 10− 18	m2/s	fitted
SEI growth reaction rate constant	kSEI	1.37 × 10− 17	m/s	fitted
Solvent bulk concentration	CS, b	4541	mol/m3	48
Diffusion coefficient of lithium ions	Di	3 × 10− 15	m2/s	48
Electrode surface area	A	0.18	m2	48
Electrode thickness	l	3.4 × 10− 5	m	48

Evolution of SEI layer

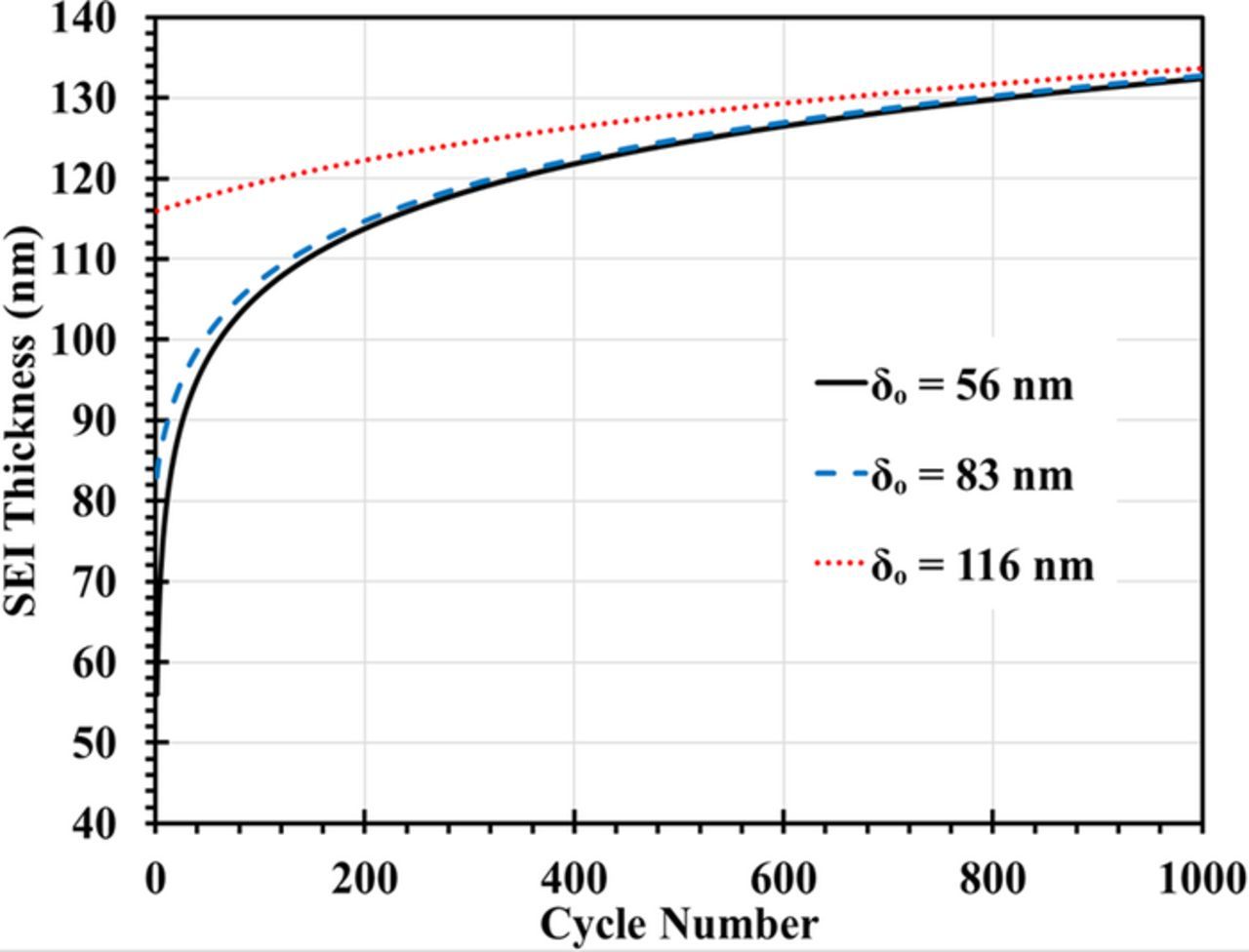
We first evaluated the impact of the SEI thickness growth on the single particle properties. From the initial SEI distribution (Eq. 17), we chose three sample particles with initial SEI thicknesses of 56 nm, 83 nm and 116 nm to simulate their SEI growth at 15°C and under a C/2 charging rate, as shown in Fig. 2. Initially, the SEI layer grows quickly. At higher cycle numbers, the rate of growth slows down due to the increasing ionic and diffusion resistance of the SEI layer. Since SEI thickness growth is slower for particles with initially thicker SEI layer, the three curves converge.

Zoom In Zoom Out Reset image size

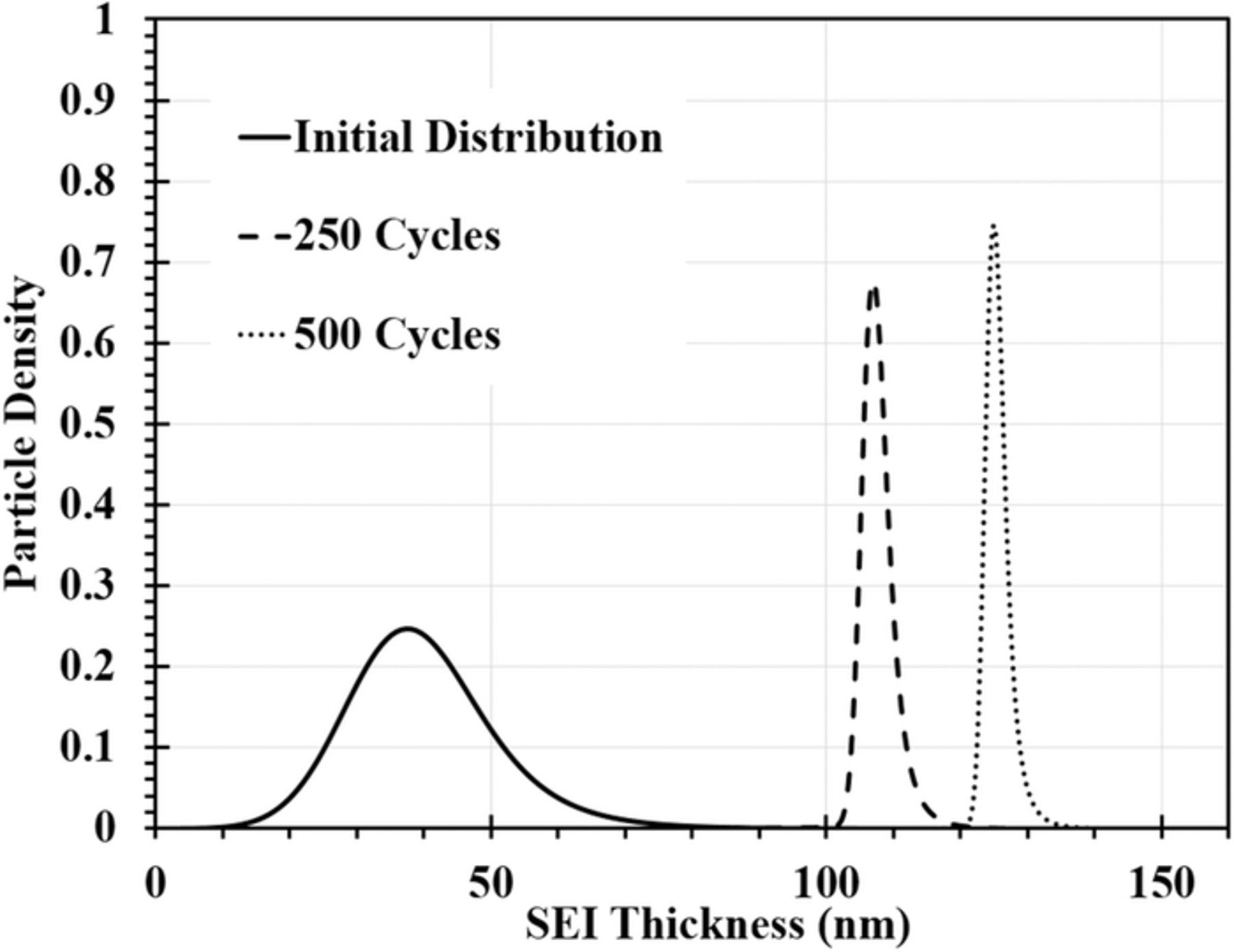
The evolution of the SEI thickness distribution during LIB cycling is shown in Fig. 3. The overarching trend is a shift of the particle density distribution to larger average SEI thickness. Since the SEI thickness grows faster on particles with smaller initial SEI thickness, the SEI distribution narrows with N, with a corresponding increase of the height of the peak.

Zoom In Zoom Out Reset image size

Effect of initial SEI distribution

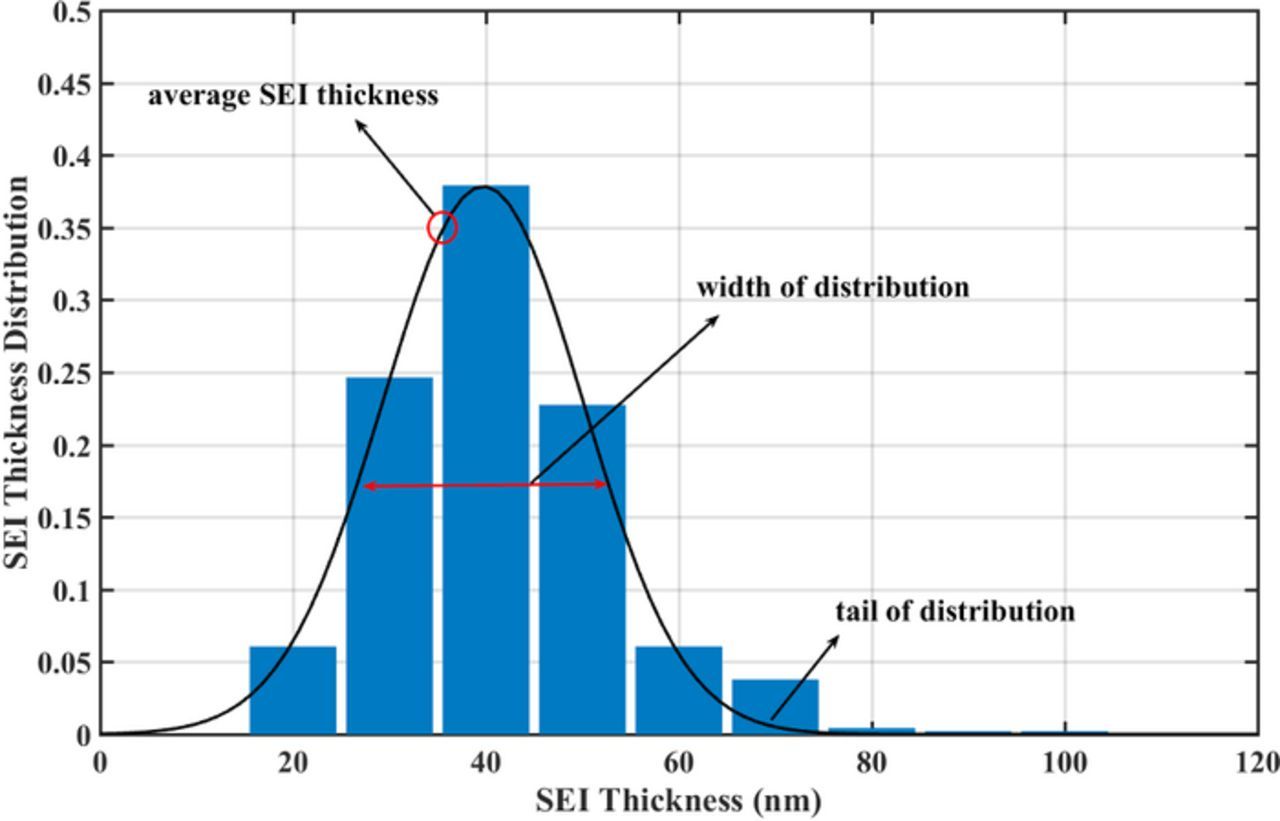
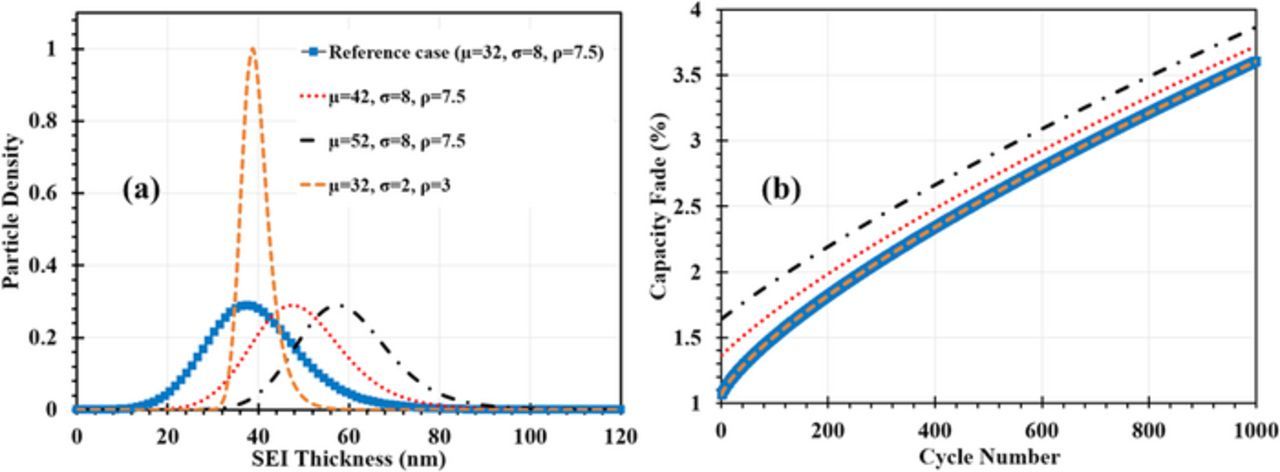
As explained in the modeling section, we use an EMG function (Eq. 17) to describe the initial SEI distribution. Fig. 4 shows the EMG function along with the SEM image analysis data. Three features determine the SEI distribution: (1) the average SEI thickness, , (2) the width, (3) and the tail of the distribution. These features can be influenced during the manufacturing process and initial conditioning of the battery. We have studied the effect of each factor on the shape of the SEI distribution and on the capacity fade.

Zoom In Zoom Out Reset image size

For comparative analyses of the impact of these characteristics, we created four initial SEI distributions, as shown in Fig. 5a: an EMG distribution as a reference case with = 40 nm; two EMG distributions with larger , which were created by increasing μ from 32 to 42 and 52; an EMG distribution with the same as the reference case but different values of σ and ρ. The capacity fade incurred by the SEI formation that occurs during the first charge-discharge cycle of the freshly made battery and during SEI growth over 1000 subsequent cycles was simulated at 15°C and under a C/2 charging rate. The results are shown in Fig. 5b.

Zoom In Zoom Out Reset image size

We found that exerts the most significant impact on Q_loss, whereas the width and the tail of the particle distribution did not exert any discernible effect. This can be seen in Fig. 5b. The curves of Q_loss for the two EMG distributions with = 40 nm but different σ and ρ lie on top of each other.

Effect of temperature on SEI thickness growth

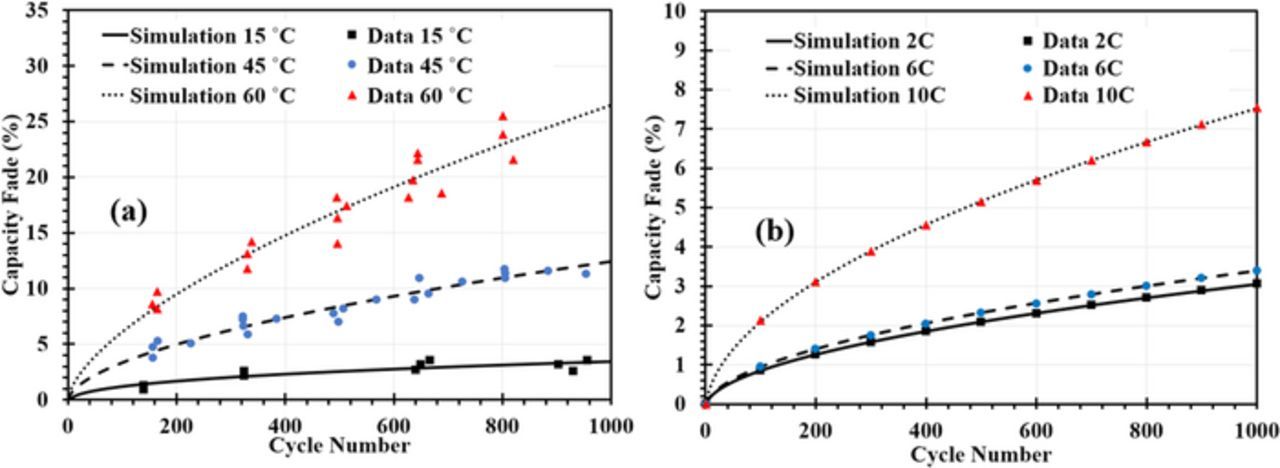
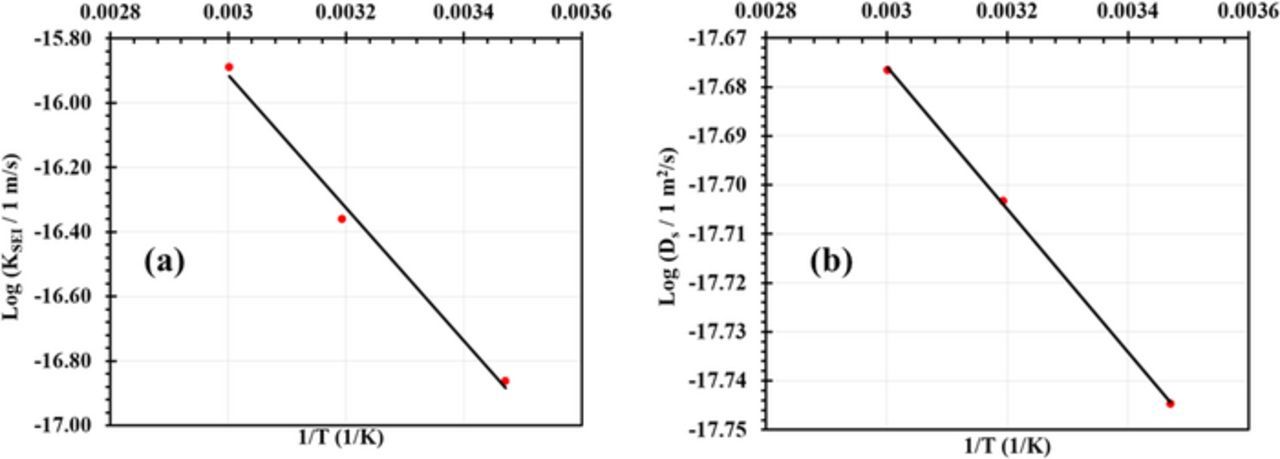
Fig. 6 shows the result of fitting the model to experimental data for Q_loss of Wang et al.⁴⁴ at T = 15°C, 45°C, and 60°C in Fig. 6a and at charging rates of 2C, 6C and 10C in Fig. 6b. The fitted curves were obtained by variation of k_SEI and D_s. Only the capacity fade caused by SEI growth was included for the comparison with experimental data. Higher T accelerates SEI growth due to the enhanced electrochemical reaction rate. The obtained model fits are in very good agreement with experimental data. From the Arrhenius plot in Fig. 7a and Fig. 7b we calculated an activation energy of 0.45 eV for the SEI growth reaction and 0.02 eV for solvent diffusion through the SEI layer. The activation energy of the SEI growth reaction in Eq. 7 is highly dependent on the surface properties of the negative electrode material and more importantly on the solvent properties.⁴⁵ Different values have been reported in the literature, ranging from 0.34 eV to 1.5 eV.^45–47 The scatter of activation energy values can be attributed to variations in cycling conditions as well as differences in materials structure and composition. For instance, we do not know what type of solvent was used by Wang et al.⁴⁴

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

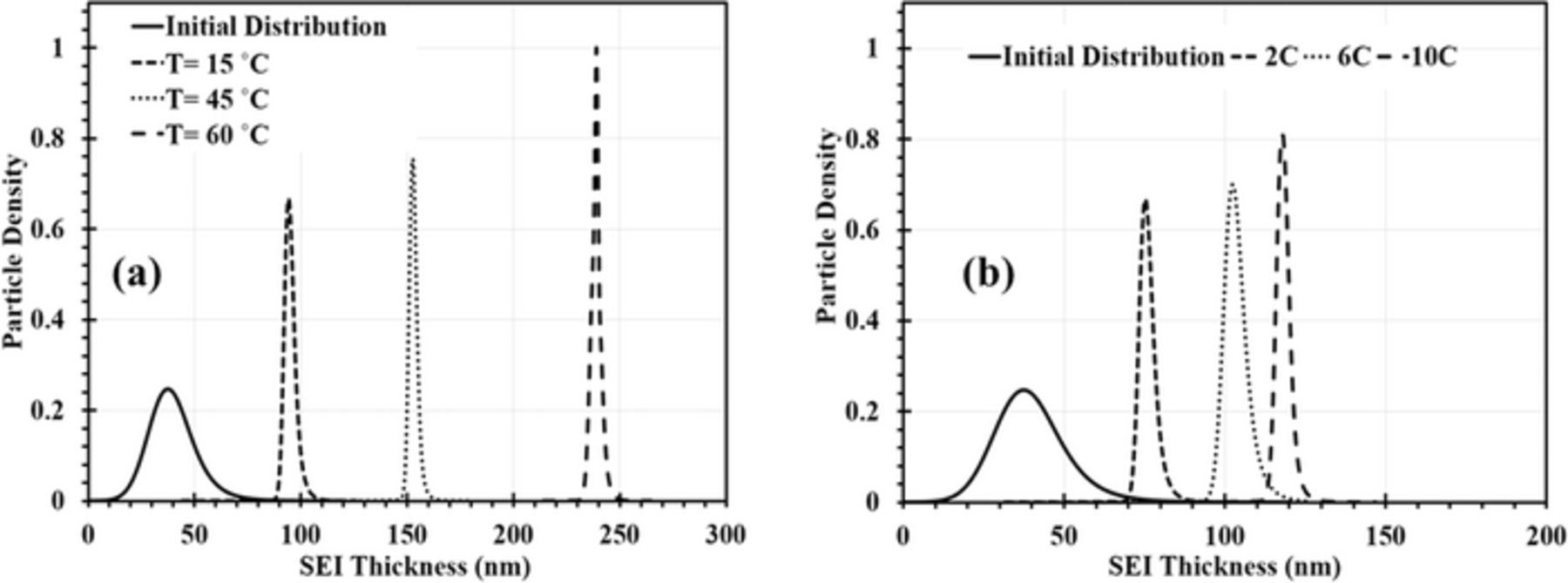
Fig. 8a shows the change in the SEI thickness distribution after 100 cycles for the three curves in Fig. 6a. When T increases, the distribution shifts to higher and the distributions becomes narrower.

Zoom In Zoom Out Reset image size

Effect of charging rate on SEI thickness growth

This article presented a statistical physics-based model to study the impact of SEI growth on the structure and performance of the negative electrode of lithium ion batteries. The two-scale approach employs a formalism based on the Fokker-Planck Equation to relate the SEI thickness growth at the single particle level to the changes in structural properties at the electrode level. The model allows exploring the correlations of structural changes that occur during charge-discharge cycling and electrode performance.

A parametric analysis of the model reveals that the first moment of the initial SEI distribution, i.e., the average SEI thickness, is the determining factor in predicting the capacity fade. The shape and width of the initial SEI distribution do not exert any discernible impact on capacity fade. During battery cycling, the SEI thickness distribution of particle-based electrodes converges toward a narrowly shaped distribution with uniform SEI thickness.

Comparison of the model to experimental data showed convincing agreement and it allows for the rate of SEI growth and the solvent diffusion coefficient to be obtained. Further analysis using Arrhenius plots provides the activation energies of these processes. Given a set of initial structural and kinetic parameters for a specific battery electrode, the model will be able to predict the evolution of electrode structure and performance upon exposure of the battery to varying life cycle protocols. The versatile modeling framework will allow incorporating further structure-transforming processes in order to systematically improve the accuracy of that prediction.

This research was conducted as part of the project entitled "Lithium ion batteries for auxiliary power units in transportation systems: from physical modeling to optimal operation", with Cool-It HiWay Services Inc. The project is supported by the Collaborative Research and Development Grants program of the Natural Sciences and Engineering Research Council of Canada (NSERC) under file No. CRDPJ 481280 – 15. The authors wish to acknowledge discussions with Dr. Kourosh Malek, Peter Johnson and Saaed Zaeri.

In order to solve the Fokker-Planck equation numerically, Eq. 16 needs to be discretized. In the following, two discretization methods are discussed: constant bin sizes and growing bin sizes. With constant bin sizes, the parameter space is discretized into finite volume elements ("bins") of constant size. When the SEI on a particle grows, this particle moves from one bin into the next. In the simplest case, all elements have the same size Δδ. With this equidistant discretization and using a central difference scheme, Eq. 16 becomes

where i is the index of the element. The size of each bin is given by

where δ_max and δ_min are the largest and the smallest SEI thickness and m is the number of elements. Rinaldo et al.³² used this discretization scheme of the Fokker-Planck Equation to calculate the evolution of the Pt nanoparticle radius distribution in PEFCs. In the current model, this method is computationally more efficient for a very fine discretization of the SEI thickness distribution, e.g., when analyzing analytical distribution functions. Since the bin sizes are constant, the evolution of the solvent and Li concentration profiles during one cycle, Eqs. 1 and 4, only need to be calculated once for each bin. The SEI growth can then be assumed to happen in discrete steps after each cycle by moving the particle from one bin to the next. This way, only the Fokker-Planck Equation needs to be solved in subsequent cycles, which reduces the simulation time. A disadvantage of this method is that in order to solve the FPE accurately, a fine discretization of the SEI thickness distribution is necessary. This is often not available from experimental data, since it would require measuring a large amount of particles to get statistically meaningful results. A second problem is that only a finite parameter space from δ_min to δ_max is simulated. Particles leaving this parameter space are lost. Therefore, it is necessary to have a sufficient number of empty bins in stock, into which particles can move. However, it is possible to estimate an upper bound for δ_maxfrom the total amount of Li in the battery.

In the second discretization method, first the initial SEI thickness distribution is discretized. Then, the SEI growth is simulated by changing the size of the bin according to the SEI growth law, while the number of particles in each bin is constant and does not need to be calculated. This way, SEI growth is simulated by stretching the initial SEI distribution along the parameter axis. With this method, the Fokker-Planck Equation does not need to be solved explicitly, but the solvent and Li concentrations have to be updated at each time step or cycle. The computation is equivalent to solving the single particle model for each bin. This makes the method computationally inexpensive if only a few bins need to be calculated. This is usually the case for experimental data from image analysis. This second method is used in the current work.