1 Introduction

The respiratory system, which includes the nose, throat, and lungs, is affected by viruses that cause influenza, sometimes known as the flu [1]. Flu is frequently characterized by acute symptoms and potentially fatal consequences. Viruses with the names influenza A, B, C, and D are four different varieties [2]. Seasonal diseases brought on by influenza types A and B occur nearly every winter. The disease brought on by type C influenza is often quite mild and frequently symptomless. Cattle are affected by type D influenza viruses, which are not known to cause any illnesses in people. All subtype of type A influenza viruses is split into strains, and each strain is additionally categorized into subcategories. Just viruses of type A have sparked pandemic. The various types of proteins found on the outside of the influenza virus envelope are designated by the letters H and N. the different influenza subtypes Hemagglutinin, also known as the HA protein, and neuraminidase, sometimes known as the NA protein, are two types of proteins that attach to the surface of viruses. The immune system of the body may produce antibodies that can identify these particular viral proteins (antigens) and hence can combat this particular influenza virus.

Scholars have identified 18 distinct HA protein forms and 11 distinct NA protein types that may co-occur in a wide range of combinations in influenza viruses that infect birds. According to reports, each of these mixtures represents a unique strain of influenza virus with a specific number of H(number) and N(number) proteins, such as \(\hbox {H}7\hbox {N}1\), \(\hbox {H}9\hbox {N}2\), \(\hbox {H}5\hbox {N}1\), etc [3, 4]. Although they might be classified as strains, type B influenza viruses are not classified into sub-types. Rarely does vaccination offer protection against novel influenza viruses. This was evident during the 2009 \(\hbox {H}1\hbox {N}1\) influenza pandemic. Antiviral medication is thus necessary to prevent the spread of the flu epidemic [5]. Resistance to the influenza virus is increasingly a problem. As an illustration, consider the \(\hbox {H}3\hbox {N}2\) and \(\hbox {H}1\hbox {N}1\) viruses’ resistance to aminoadamantanes and oseltamivir, respectively [8,9,10]. Future pandemics might be brought on through resistance, which is lethal. In comparison to the original strain, a new strain’s force of transmission is typically thought to be quite weak. According to references [10,11,12], mutation reduces the viral strength, which is connected to this event.

In epidemiology, mathematical modelling is crucial for a deeper understanding of the numerous facets of many illnesses. Because there are several diseases in which more than one pathogen strain is noted due to the process of viral mutation, for example, influenza [32], human immunodeficiency virus [33], tuberculosis [34], and COVID-19 [35], multi-strain epidemics models have attracted the focus of many researchers. Recently, in [26,27,28], the research of the two-strain epidemic model by fractional differential equation was also established, because the fractional-order differential equations can be helpful in modelling biological systems [29,30,31]. In actuality, some unknown environmental perturbations invariably affect population dynamics and epidemic systems. As we all know, real life is filled with randomness and unpredictability. Stochastic models can better conform to the actual situation, because most epidemic models are influenced by environmental factors, such as percipitation, temperature, relative humidity. Thus, the variability of epidemic growth and spread is random due to the different infectious periods. It has equally been shown that stochastic models can provide additional degree of realism as compared with their deterministic study. Furthermore, several writers have extensively examined certain stochastic epidemics models, including [36,37,38,39,40]. An epidemic model with a twofold hypothesis that combines two transmission mechanisms, SIS and SIR, with two distinct saturation incidence rates is addressed in [36] Boukanjime et al. Although there might be two epidemic illnesses in the current world, one brought on by virus A and the other by virus B, the authors of [37] explored an SIS model with the twin epidemic theory. With two distinct saturation incidence rates, Chang et al. [38] constructed a stochastic SIRS model and determined the thresholds that determine whether the disease will remain or go away. The existence of an ergodic stationary distribution of the nonnegative solutions to a stochastic SIS epidemic model with double illnesses and the Beddington-DeAngelis incidence was demonstrated by Liu and Jiang, who used [39] as their source. In [40], it was looked at how two different infectious diseases might spread vertically under a stochastic epidemic model.

In our case we will study two strains of an influenza epidemic model, after analyze the situation in which the two strains can coexist and the difference in their mode of transmission, we employ the use of mathematical modeling. Principal element in mathematical modeling is the incidence rate. Its significance in epidemiology can’t be over emphasized.

Recently, Baba et al. [41] constructed and studied a resistance and non-resistance strains of influenza.

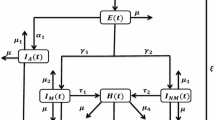
$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle \dfrac{\mathrm {d} S(t)}{\mathrm {d} t}= \Lambda - \alpha S(t) I_N(t) - \dfrac{\beta S(t) I_R(t)}{1+\kappa I_R(t)}-d S(t) ,\\ \\ \displaystyle \dfrac{\mathrm {d} I_N(t)}{\mathrm {d} t} = \alpha S(t) I_N(t) - (d + \mu )I_N(t),\\ \\ \displaystyle \dfrac{\mathrm {d} I_R(t)}{\mathrm {d} t} = \dfrac{\beta S(t) I_R(t)}{1+\kappa I_R(t)}-(d + \gamma )I_R(t) ,\\ \\ \displaystyle \dfrac{\mathrm {d} R(t)}{\mathrm {d} t} = \mu I_N(t) + \gamma I_R(t) -d R(t). \end{array} \right. \end{aligned}$$
(1.1)

Here S(t) is the susceptibles, \(I_R(t)\) is the infective resistant individuals, \(I_N(t)\) is the infective non-resistant individuals and R(t) is the removed ones. The parameters in the model (1.1) are positive constants where : \(\Lambda\) is a recruitment into susceptible. \(\dfrac{1}{d}\) is natural mortality rate, The rate of infection by resistant strain is represented by \(\alpha\), the rate of infection by non-resistant strain is denoted by \(\beta\), removal of individuals carrying the resistant strain from the population is \(\frac{1}{\gamma }\), removal of individuals carrying the non-resistant strain is \(\frac{1}{\mu }\), and the mutation effect on the resistant strain is \(\kappa\). Both illnesses are spread by interaction between people in the susceptible compartment and those in the \(I_N\) and \(I_R\) compartments, which have, respectively, bilinear and saturation incidence rates. We anticipate that the populations that reside in environments where random accidents are prevalent are mostly impacted by the contact rate, which will primarily present itself as changes in the saturated response rate, so that \(\alpha\) turn into \(\alpha + \sigma _N {\dot{B}}(t)\) and \(\beta\) turn into \(\beta + \sigma _R {\dot{B}}(t)\) where \(B_N(t)\) and \(B_R(t))\) are standard Brownian motion with intensities \(\sigma _N>0\) and \(\sigma _R>0\). Now, the corresponding stochastic model of the system (1.1) is as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle \mathrm {d} S(t)=\bigg ( \Lambda - \alpha S(t) I_N(t) - \dfrac{\beta S(t) I_R(t)}{1+\kappa I_R(t)}-d S(t) \bigg ) \mathrm {d} t- \sigma _N S(t)I_N(t)\mathrm {d} B_N(t)-\dfrac{\sigma _R S(t) I_R(t)}{1+\kappa I_R(t)} \mathrm {d} B_R(t) ,\\ \\ \displaystyle \mathrm {d} I_N(t) = \bigg ( \alpha S(t) I_N(t) - (d + \mu )I_N(t) \bigg ) \mathrm {d} t+\sigma _N S(t)I_N(t)\mathrm {d} B_N(t),\\ \\ \displaystyle \mathrm {d} I_R(t) = \bigg ( \dfrac{\beta S(t) I_R(t)}{1+\kappa I_R(t)}-(d + \gamma )I_R(t) \bigg ) \mathrm {d}t+\dfrac{\sigma _R S(t) I_R(t)}{1+\kappa I_R(t)} \mathrm {d} B_R(t) ,\\ \\ \displaystyle \mathrm {d} R (t) = \bigg ( \mu I_N(t) + \gamma I_R(t) -d R(t) \bigg )\mathrm {d} t. \end{array} \right. \end{aligned}$$
(1.2)
Fig. 1
figure 1

The detailed flowchart of system (1.2)

Full size image

The remaining of this paper is arranged as: In the Sect. 2, we show the positivity and the boundedness of solutions of the stochastic system (1.2). The extinction of the non-resistance and resistance infectious diseases will be discussed in Sect. 3. In Sect. 4 we study the persistence in mean of the epidemic. In Sect. 5, the numerical simulations are carried out to confirm our theoretical results. Lastly, a brief discussion is given in the end to conclude this paper.

2 Existence and uniqueness of the global nonnegative solution

The notations, definitions, and lemmas we utilised to examine our primary outcomes are provided in this part.

Consider a filtration \({ \lbrace {\mathscr {F}}_t \rbrace _{t \ge 0}}\) with a complete probability space \(\left( \Omega , {\mathscr {F}},\left\{ {\mathscr {F}}_t\right\} _{t \ge 0}, {\mathbb {P}}\right)\) that fulfills the usual conditions with increasing and right continuous while \({\mathscr {F}}_0\) is the set of \({\mathbb {P}}\)-null sets. The function B(t) denotes a scalar Brownian motion which is defined on \(\Omega\).

We introduce the following notations:

$$\begin{aligned} {\mathbb {R}}_{+}^d=\left\{ x=\left( x_1, \ldots , x_d\right) \in {\mathbb {R}}^d: x_i>0,1 \le i \le d\right\} \text{ and } \overline{{\mathbb {R}}}_{+}^d=\left\{ x=\left( x_1, \ldots , x_d\right) \in {\mathbb {R}}^d: x_i \ge 0,1 \le i \le d\right\} . \end{aligned}$$

In general, consider the d-dimensional stochastic differential equation

$$\begin{aligned} d X(t)=f(X(t)) d t+g(X(t)) d B(t) \text{ for } t \ge t_0, \end{aligned}$$

with initial value \(X(0)=X_0 \in {\mathbb {R}}^d\). B(t) denotes a d-dimensional standard Brownian motion defined on the complete probability space \(\left( \Omega , {\mathscr {F}},\left\{ {\mathscr {F}}_t\right\} _{t \ge 0}, {\mathbb {P}}\right)\). Denote by \(C^2\left( {\mathbb {R}}^d ; \overline{{\mathbb {R}}}_{+}\right)\)the family of all nonnegative functions V(X) defined on \({\mathbb {R}}^d\) such that they are continuously twice differentiable in X. The differential operator L of Eq. (1.5) is defined by [42]

$$\begin{aligned} L=\sum _{i=1}^d f_i(X) \frac{\partial }{\partial X_i}+\frac{1}{2} \sum _{i, j=1}^d\left[ g^T(X) g(X)\right] _{i j} \frac{\partial ^2}{\partial X_i \partial X_j}. \end{aligned}$$

If L acts on a function \(V \in C^2\left( {\mathbb {R}}^d ; \overline{{\mathbb {R}}}_{+}\right)\), then

$$\begin{aligned} L V(X)=V_X(X) f(X)+\frac{1}{2} {\text {trace}}\left[ g^T(X) V_{X X}(X) g(X)\right] , \end{aligned}$$

where \(V_X=\left( \frac{\partial V}{\partial X_1}, \ldots , \frac{\partial V}{\partial X_d}\right) , V_{X X}=\left( \frac{\partial ^2 V}{\partial X_i \partial X_j}\right) _{d \times d}\).

In view of Itô’s formula [42], if \(X(t) \in {\mathbb {R}}^d\), then

$$\begin{aligned} d V(X(t))=L V(X(t)) d t+V_X(X(t)) g(X(t)) d B(t). \end{aligned}$$

For arbitrary integrable function h on \([0,+\infty )\), define \(\langle h (t)\rangle = \dfrac{\int _{0}^{t} h(\theta ) \, \mathrm {d} \theta }{t}\).

Let \({\mathbf {S}}(t)=(S(t), I_N(t), I_R(t),R(t))\) and \({\mathbf {S}}_0=(S(0), I_N(0), I_R(0),R(0)).\)

Definition 1

  1. 1.

    The diseases \(I_N(t)\) and \(I_R(t)\) are said to go extinction if \(\lim \nolimits _{t \rightarrow +\infty } I_N(t)=0\) and \(\lim \nolimits _{t \rightarrow +\infty } I_R(t)=0\).

  2. 2.

    The diseases \(I_N(t)\) and \(I_R(t)\) will be persist in mean if \(\exists\) \(a_1>0\) and \(a_2>0\) such that \(\liminf \nolimits _{t \rightarrow +\infty } \langle I_N(t)\rangle \geqslant a_1\) and \(\liminf \nolimits _{t \rightarrow +\infty } \langle I_R(t)\rangle \geqslant a_2.\)

Remark 2

Let the set

$$\begin{aligned} \Gamma = \left\{(S(t),I_N(t),I_R(t),R(t)) \in {\mathbb {R}}_+^{4} : S(t)+I_N(t)+I_R(t)+R(t) \le \dfrac{\Lambda }{d} \right\} . \end{aligned}$$

The total population \(N(t)=S(t)+I_N(t)+I_R(t)+R(t)\) in systems (1.1) and (1.2) verifies, the equation

$$\begin{aligned} \dfrac{\mathrm {d} N(t)}{\mathrm {d} t} \le \Lambda -dN(t), \end{aligned}$$

which gives by integration

$$\begin{aligned} N(t) \le e^{-dt}\left(N(0) - \dfrac{\Lambda }{d}\right) + \dfrac{\Lambda }{d} \le \max \left(N(0),\dfrac{\Lambda }{d}\right). \end{aligned}$$

If \({\mathbf {S}}_0 \in \Gamma\), then \(N(t) \le \dfrac{\Lambda }{d}\) almost surely. Thus, the set \(\Gamma\) is almost surely positively invariant by the systems (1.1) and (1.2) respectively, throughout the rest, we assume that \({\mathbf {S}}_0\in \Gamma .\)

Lemma 3

For the initial condition \({\mathbf {S}}_0\in \Gamma\), the model (1.2) has at most one solution and will belong to \({\mathbb {R}}_+^{4}\) with probability one \(\forall\) \(t \geqslant 0\) almost surely.

Proof

As all the coefficients of the proposed stochastic model (1.2) are locally Lipschitz continuous, then for each initial condition \({\mathbf {S}}_0\in {\mathbb {R}}_+^{4}\), \(\exists\) exclusive local solution \({\mathbf {S}}(t)\) on \(t \in [0, \tau _e)\), where \(\tau _e\) denotes the explosion time.

It is obligatory to verify that the solution is global, one need only to prove that \(\tau _e= \infty\) almost surely.

For this, let us take \(m_0 \ge 1\) sufficiently large to get that \({\mathbf {S}}_0\in [ \dfrac{1}{m_0},m_0]\), \(\forall\) integer \(m_0 \le m\). Next, we express the stopping time by:

$$\begin{aligned} \tau _m = \inf \left \{t \in [0, \tau _e) : S(t) \notin \left(\dfrac{1}{m},m\right), \; \text {or} \; I_N(t)\notin \left(\dfrac{1}{m},m\right), \; \text {or} \; I_R(t)\notin \left(\dfrac{1}{m},m\right), \; \text {or} \; R(t) \notin \left(\dfrac{1}{m},m\right) \right \}, \end{aligned}$$
(2.1)

where one can set \(\inf \emptyset = \infty\). Thus, \(\tau _m\) increases as m tends to \(\infty\).

Let \(\tau _{\infty } = \lim \nolimits _{m \rightarrow +\infty } \tau _m\), and \(\tau _{\infty } \leqslant \tau _e\) almost surely. When \(\tau _{\infty }= \infty\) almost surely is true, then \(\tau _e= \infty\) almost surely and \({\mathbf {S}}(t)\in {\mathbb {R}}_+^{4}\) almost surely \(\forall\) \(t \geqslant 0\). To put it another way, we just need to demonstrate that \(\tau _{\infty }=\infty\) almost surely. Otherwise, there will be constants \({\mathcal {T}}>0\) and \(0<\varepsilon <1\) with

$$\begin{aligned} \varepsilon < {{\mathbb {P}}} \lbrace \tau _{\infty } \leqslant {\mathcal {T}} \rbrace . \end{aligned}$$
(2.2)

So, \(\exists\) \(m_0 \geqslant m_1\) with

$$\begin{aligned} \varepsilon \le {{\mathbb {P}}} \lbrace {\mathcal {T}}\ge \tau _m \rbrace , \ \; \forall \; m_1 \leqslant m. \end{aligned}$$
(2.3)

Let us take a \({\mathcal {C}}^2\)-function as

$$\begin{aligned} {\mathcal {V}}(S,I_N,I_R,R)= \chi (S)+\chi (I_N)+\chi (I_R)+\chi (R), \end{aligned}$$
(2.4)

where \(\chi (x) = -1+x- \log x\), \(\forall x \in ]0, + \infty [\)

Applying the Itô’s method on \({\mathcal {V}}\), one get

$$\begin{aligned} \mathrm {d} {\mathcal {V}}(S,I_N,I_R,R)= {{\mathcal {L}}}{{\mathcal {V}}}(S,I_N,I_R,R) \mathrm {d} t + \sigma _N (I_N - S)\mathrm {d}B_N(t) + \dfrac{\sigma _R(I_R - S)}{1+ \kappa I_R}\mathrm {d}B_R(t), \end{aligned}$$
(2.5)

where \({{\mathcal {L}}}{{\mathcal {V}}}: {\mathbb {R}}_+^{4} \rightarrow {\mathbb {R}}^{4}\) is defined by

$$\begin{aligned} {{\mathcal {L}}}{{\mathcal {V}}}&= \Lambda + 4d - \frac{\Lambda }{S} -dS + \alpha I_N + \dfrac{\beta I_R}{1+ \kappa I_R}+ \dfrac{\sigma _N^2 I_N^2}{2} + \dfrac{\sigma _R^2 I_R^2}{2(1+ \kappa I_R)^2} \end{aligned}$$
(2.6)
$$\begin{aligned}&\quad - d I_N - \alpha S + \mu + \dfrac{\sigma _N^2 S^2}{2} - dI_R + \dfrac{\sigma _R^2 S^2}{2(1+ \kappa I_R)^2} \nonumber \\&\quad - \dfrac{\beta S}{1+k I_R} + \gamma -dR - \dfrac{\mu I_N}{R} - \dfrac{\gamma I_R}{R} \nonumber \\&\le \Lambda + 4d + \alpha I_N + \dfrac{\beta }{\kappa } + \mu + \gamma +\dfrac{\sigma _N^2 I_N^2}{2} + \dfrac{\sigma _R^2 }{2 \kappa ^2} + \dfrac{\sigma _N^2 S^2}{2} + \dfrac{\sigma _R^2 S^2}{2(1+ \kappa I_R)^2} \nonumber \\&\le \Lambda + 4d + \alpha \dfrac{\Lambda }{d} + \dfrac{\beta }{\kappa } + \mu + \gamma +\dfrac{\sigma _N^2 \Lambda ^2}{2 d^2} + \dfrac{\sigma _R^2 }{2 \kappa ^2} + \dfrac{\sigma _N^2 \Lambda ^2}{2 d^2} + \dfrac{\sigma _R^2 \Lambda ^2}{2 \kappa d^2} := {\mathcal {M}}. \end{aligned}$$
(2.7)

Thus

$$\begin{aligned} \mathrm {d} {\mathcal {V}}(S,I_N,I_R,R) \le {\mathcal {M}}\mathrm {d}t + \sigma _N (I_N - S)\mathrm {d}B_N(t) + \dfrac{\sigma _R(I_R - S)}{1+ \kappa I_R}\mathrm {d}B_R(t). \end{aligned}$$
(2.8)

Integrating (2.8) from 0 to \(\tau _m \wedge {\mathcal {T}} = \min \lbrace \tau _m , {\mathcal {T}} \rbrace\) and then using the notion of expectations, we have

$$\begin{aligned} {\mathbb {E}} {\mathcal {V}} \bigg (S(\tau _m \wedge {\mathcal {T}}),I_N(\tau _m \wedge {\mathcal {T}}),I_R(\tau _m \wedge {\mathcal {T}}),R(\tau _m \wedge {\mathcal {T}}) \bigg ) \le {\mathcal {V}} \bigg ({\mathbf {S}}_0\bigg ) + {{\mathcal {M}}}{{\mathcal {T}}}. \end{aligned}$$
(2.9)

Let \(\Omega _m = \lbrace \tau _m \le {\mathcal {T}} \rbrace\) for \(m_1\le m\). Using (2.3), one can acquire \({{\mathbb {P}}}(\Omega _m) \ge \varepsilon .\) Notice that \(\forall\) \(\varpi \in \Omega _m\), \(\exists\) \(S(\tau _m,\varpi )\) or \(I_N(\tau _m,\varpi )\) or \(I_R(\tau _m,\varpi )\) or \(R(\tau _m,\varpi )\) equals either m or \(\dfrac{1}{m}.\)

Therefore,

$$\begin{aligned} {\mathcal {V}} \bigg (S(\tau _m,\varpi ),I_N(\tau _m,\varpi ),I_R(\tau _m,\varpi ),R(\tau _m,\varpi )) \bigg ) \ge \bigg ( m-1-\log m \bigg ) \wedge \bigg ( \dfrac{1}{m}-1+\log m \bigg ). \end{aligned}$$

Then we attain

$$\begin{aligned} {\mathcal {V}} \bigg ({\mathbf {S}}_0 \bigg ) + {{\mathcal {M}}}{{\mathcal {T}}}&\ge {\mathbb {E}} \bigg ( 1_{\Omega _m} {\mathcal {V}} \Big (S(\tau _m,\varpi ),I_N(\tau _m,\varpi ),I_R(\tau _m,\varpi ),R(\tau _m,\varpi ) \Big ) \bigg ) \nonumber \\&\ge \varepsilon \bigg ( m-1-\log m \bigg ) \wedge \bigg ( \dfrac{1}{m}-1+\log m \bigg ), \end{aligned}$$
(2.10)

where \(1_{\Omega _m(\varpi )}\) is the indicator function of \(\Omega _m\). For \(m \rightarrow \infty\), one reach

$$\begin{aligned} \infty > {\mathcal {V}} \bigg ({\mathbf {S}}_0 \bigg ) + {{\mathcal {M}}}{{\mathcal {T}}} = \infty , \end{aligned}$$
(2.11)

is a contradiction. Hence, \(\tau _{\infty } = \infty\). \(\hfill\square\)

Lemma 4

[42] Let \({\mathbf {S}}(t)\) satisfies model (1.2) with \({\mathbf {S}}_0\in \Gamma\). Then

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{1}{t} \displaystyle \int _{0}^{t} \dfrac{\sigma _R S(\zeta )}{1+ \kappa I_R(\zeta )} \, \mathrm {d} B_R(\zeta )=0, \qquad \lim \limits _{t \rightarrow + \infty } \dfrac{1}{t} \displaystyle \int _{0}^{t} \sigma _N S(\zeta ) \, \mathrm {d} B_N(\zeta )=0, \qquad \lim \limits _{t \rightarrow + \infty } \dfrac{1}{t} \displaystyle \int _{0}^{t} \sigma _R S(\zeta ) \, \mathrm {d} B_R(\zeta )=0. \end{aligned}$$
(2.12)

3 Extinction

Here, we create the conditions that result in extinction of the non-resistance and resistance infectious strains motioned in the system (1.2).

Proposition 5

If

$$\begin{aligned} \sigma _N > \dfrac{\alpha }{\sqrt{2(d+\mu )}} \end{aligned}$$
(3.1)

then the non-resistance strain of (1.2) go to the extinction almost surely.

Proof

Let \({\mathbf {S}}(t)\) satisfies the model(1.2) with \({\mathbf {S}}_0\in \Gamma\). Using the Itô’s method, one get

$$\begin{aligned} \mathrm {d} \log I_N(t)&= \Big ( \alpha S(t) -(d+ \mu ) - \dfrac{ \sigma _N^2 S^2(t)}{2} \Big ) \mathrm {d} t + \sigma _N S(t) \mathrm {d} B_N(t) \nonumber \\&\le \bigg [ -\dfrac{ \sigma _N^2 }{2} \Big ( S(t) - \dfrac{ \alpha }{ \sigma _N^2} \Big )^2 + \dfrac{ \alpha ^2}{2 \sigma _N^2} -(d+ \mu ) \bigg ] \mathrm {d} t + \sigma _N S(t) \mathrm {d} B_N(t) \end{aligned}$$
(3.2)
$$\begin{aligned}&\le \bigg [ \dfrac{ \alpha ^2}{2 \sigma _N^2} -(d+ \mu ) \bigg ]\mathrm {d}t +\sigma _N S(t) \mathrm {d} B_N(t). \end{aligned}$$
(3.3)

Integrating (3.3) from 0 to t and doing some manipulation, we obtain

$$\begin{aligned} \dfrac{\log I_N(t)}{t} \le - \Big ( d+ \mu - \dfrac{\alpha ^2}{2 \sigma _N^2} \Big ) + \dfrac{{\mathcal {M}}_N (t)}{t}+ \dfrac{\log I_N(0)}{t}, \end{aligned}$$
(3.4)

where \({\mathcal {M}}_N (t)= \displaystyle \int _{0}^{t} \sigma _N S(\zeta ) \, \mathrm {d} B_N(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_N (0)=0\), and by the Lemma 4, we obtain

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_N (t)}{t} = 0. \end{aligned}$$
(3.5)

Since \(\sigma _N > \dfrac{\alpha }{\sqrt{2(d+\mu )}}\). Applying superior limit of 3.4, we conclude

$$\begin{aligned} \limsup \limits _{t \rightarrow + \infty } \dfrac{\log I_N(t)}{t} \le - \Big ( d+ \mu - \dfrac{\alpha ^2}{2 \sigma _N^2} \Big ) < 0, \end{aligned}$$
(3.6)

which means that \(\limsup \limits _{t \rightarrow + \infty } I_N(t) =0\) almost surely. Hence the theorem. \(\hfill\square\)

Proposition 6

If

$$\begin{aligned} \sigma _R > \dfrac{\beta }{\sqrt{2(d+ \gamma )}}, \end{aligned}$$
(3.7)

then the resistance strain of (1.2) go to the extinction almost surely.

Proof

Let \({\mathbf {S}}(t)\) satisfies the model (1.2) with \({\mathbf {S}}_0\in \Gamma\). Implementing the Itô’s technique on model (1.2) results in

$$\begin{aligned} \mathrm {d} \log I_R(t)&= \Big ( \dfrac{\beta S(t) }{1+\kappa I_R(t)} -(d+ \gamma ) - \dfrac{ \sigma _R^2 S^2(t)}{2(1+\kappa I_R(t))^2} \Big ) \mathrm {d} t + \dfrac{ \sigma _R S(t)}{1+\kappa I_R(t)} \mathrm {d} B_R(t) \nonumber \\&\le \bigg [ -\dfrac{ \sigma _R^2 }{2} \Big ( \dfrac{\beta S(t) }{1+\kappa I_R(t)} - \dfrac{ \beta }{ \sigma _R^2} \Big )^2 + \dfrac{ \beta ^2}{2 \sigma _R^2} -(d+ \gamma ) \bigg ] \mathrm {d} t + \dfrac{ \sigma _R S(t)}{1+\kappa I_R(t)} \mathrm {d} B_R(t) \end{aligned}$$
(3.8)
$$\begin{aligned}&\le \bigg [ \dfrac{ \beta ^2}{2 \sigma _R^2} -(d+ \gamma ) \bigg ]\mathrm {d}t + \dfrac{ \sigma _R S(t)}{1+\kappa I_R(t)} \mathrm {d} B_R(t). \end{aligned}$$
(3.9)

Integrating Eq. (3.9), we reach

$$\begin{aligned} \dfrac{\log I_R(t)}{t} \le - \Big ( d+ \gamma - \dfrac{\beta ^2}{2 \sigma _R^2} \Big ) + \dfrac{{\mathcal {M}}_R (t)}{t}+ \dfrac{\log I_R(0)}{t}, \end{aligned}$$
(3.10)

where \({\mathcal {M}}_R (t)= \displaystyle \int _{0}^{t} \dfrac{ \sigma _R S(\zeta )}{1+\kappa I_R(\zeta )} \, \mathrm {d} B_R(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_R (0)=0\), and by the Lemma 4, one may reach

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_R (t)}{t} = 0. \end{aligned}$$
(3.11)

Since \(\sigma _R > \dfrac{\beta }{\sqrt{2(d+\gamma )}}\). Applying superior limit to (3.10), we conclude

$$\begin{aligned} \limsup \limits _{t \rightarrow + \infty } \dfrac{\log I_R(t)}{t} \le - \Big ( d+ \gamma - \dfrac{\beta ^2}{2 \sigma _R^2} \Big ) < 0, \end{aligned}$$
(3.12)

which implies that \(\limsup \limits _{t \rightarrow + \infty } I_R(t) =0\) almost surely. \(\square\)

Remark 7

Proposition 5 and Proposition 6 shows that when \(\sigma _N > \dfrac{\alpha }{\sqrt{2(d+\mu )}}\) and \(\sigma _R > \dfrac{\beta }{\sqrt{2(d+ \gamma )}}\) the non-resistance strain and resistance strain of system (1.2) die out almost surely, respectively. In other words, large white noise stochastic disturbance yield the two strains extinct. Hence, we presume that the white noise disturbance is not large in the rest of this manuscript.

Let

$$\begin{aligned}&{\mathcal {R}}_N^s = \dfrac{\alpha \Lambda }{d(d+ \mu )} - \dfrac{\sigma _N^2 \Lambda ^2}{2 d^2(d+ \mu )}, \\&\quad {\mathcal {R}}_R^s = \dfrac{\beta \Lambda }{d(d+ \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2 d^2(d+ \gamma )}. \end{aligned}$$

Theorem 8

Let \({\mathbf {S}}(t)\) satisfies the model (1.2) with \({\mathbf {S}}_0\in \Gamma\).

  1. 1.

    If \({\mathcal {R}}_N^s <1\) and \(\sigma _N \leqslant \sqrt{ \dfrac{2 d \alpha }{\Lambda }}\) then the non-resistant strain of system (1.2) exhibits extinction almost surely, i.e

    $$\begin{aligned} \lim \limits _{t \rightarrow + \infty } I_N(t)= 0. \end{aligned}$$
  2. 2.

    If \({\mathcal {R}}_R^s <1\) and \(\sigma _R \leqslant \sqrt{ \dfrac{2 d \beta }{\Lambda }}\) then the resistant strain of system (1.2) exhibits extinction almost surely, i.e

    $$\begin{aligned} \lim \limits _{t \rightarrow + \infty } I_R(t)= 0 , \end{aligned}$$

    Meanwhile, \(\lim \limits _{t \rightarrow + \infty } S(t)= \dfrac{\Lambda }{d}\), and \(\lim \limits _{t \rightarrow + \infty } R(t)= 0\).

Proof

Firstly, taking integral of both sides of (3.2) and doing some manipulations gives

$$\begin{aligned} \dfrac{\log I_N(t)}{t}&= \dfrac{1}{t} \displaystyle \int _{0}^{t} \Big (\alpha S(\tau ) - (d+ \mu ) - \dfrac{ \sigma _N^2 S^2(\tau )}{2} \Big ) \, \mathrm {d} \tau + \dfrac{{\mathcal {M}}_N (t)}{t}+ \dfrac{\log I_N(0)}{t} \nonumber \\&\le \Big (\dfrac{\alpha \Lambda }{d} - (d+ \mu ) - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2} \Big )+ \dfrac{{\mathcal {M}}_N (t)}{t}+ \dfrac{\log I_N(0)}{t}\nonumber \\&= (d + \mu )\Big (\dfrac{\alpha \Lambda }{d(d+ \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2(d+ \mu )} -1 \Big )+ \dfrac{{\mathcal {M}}_N (t)}{t}+ \dfrac{\log I_N(0)}{t} \end{aligned}$$
(3.13)
$$\begin{aligned} = (d + \mu )\Big ({\mathcal {R}}_N^s -1 \Big ) + \dfrac{{\mathcal {M}}_N (t)}{t}+ \dfrac{\log I_N(0)}{t}, \end{aligned}$$
(3.14)

where \({\mathcal {M}}_N (t)= \displaystyle \int _{0}^{t} \sigma _N S(\zeta ) \, \mathrm {d} B_N(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_N (0)=0\), and by the Lemma 4, one have

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_N (t)}{t} = 0. \end{aligned}$$
(3.15)

Using superior limit on Eq. (3.14), one get

$$\begin{aligned} \limsup \limits _{t \rightarrow +\infty } \dfrac{ \log I_N(t)}{t} \le (d + \mu )\Big ({\mathcal {R}}_N^s -1 \Big ) <0. \end{aligned}$$
(3.16)

Consequently, \(\lim \nolimits _{t \rightarrow + \infty } I_N(t)= 0\), almost surely.

Secondly, for both sides of (3.8), integrating from 0 to t first and doing some manipulations gives

$$\begin{aligned} \dfrac{\log I_R(t)}{t}&= \dfrac{1}{t} \displaystyle \int _{0}^{t} \Big (\dfrac{\beta S(\tau ) }{1+\kappa I_R(\tau )} - (d+ \gamma ) - \dfrac{ \sigma _R^2 S^2(\tau )}{2(1+\kappa I_R(\tau ))^2} \Big ) \, \mathrm {d} \tau + \dfrac{{\mathcal {M}}_R (t)}{t}+ \dfrac{\log I_R(0)}{t} \nonumber \\&\le \Big (\dfrac{\beta \Lambda }{d} - (d+ \gamma ) - \dfrac{ \sigma _R^2 \Lambda ^2}{2d^2} \Big )+ \dfrac{{\mathcal {M}}_R (t)}{t}+ \dfrac{\log I_R(0)}{t} \nonumber \\&= (d + \gamma )\Big (\dfrac{\beta \Lambda }{d(d+ \gamma )} - \dfrac{ \sigma _R^2 \Lambda ^2}{2d^2(d+ \gamma )} -1 \Big )+ \dfrac{{\mathcal {M}}_R (t)}{t}+ \dfrac{\log I_R(0)}{t} \end{aligned}$$
(3.17)
$$\begin{aligned}&= (d + \gamma )\Big ({\mathcal {R}}_R^s -1 \Big ) + \dfrac{{\mathcal {M}}_R (t)}{t}+ \dfrac{\log I_R(0)}{t}, \end{aligned}$$
(3.18)

where \({\mathcal {M}}_R (t)= \displaystyle \int _{0}^{t} \dfrac{ \sigma _R S(\zeta )}{1+\kappa I_R(\zeta )} \, \mathrm {d} B_R(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_R (0)=0\), and by the Lemma 4, one have

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_R (t)}{t} = 0. \end{aligned}$$
(3.19)

We achieve the following result by using superior limit

$$\begin{aligned} \limsup \limits _{t \rightarrow +\infty } \dfrac{ \log I_R(t)}{t} \le (d + \gamma )\Big ({\mathcal {R}}_R^s -1 \Big ) <0, \end{aligned}$$
(3.20)

Consequently, \(\lim \nolimits _{t \rightarrow + \infty } I_R(t)= 0\), almost surely.

Lastly, without loss of generality, one can suppose that \(0< I_N(t) < \varepsilon _N\) and \(0< I_R(t) < \varepsilon _R\) \(\forall\) \(t \ge 0\), from the first class of the model (1.2), one obtain

$$\begin{aligned} \dfrac{ \mathrm {d} S(t)}{ \mathrm {d} t} \ge \Lambda - \Big ( d+ \alpha \varepsilon _N + \beta \varepsilon _R + \sigma _N \varepsilon _N \vert {\dot{B}}_N \vert + \sigma _R \varepsilon _R \vert {\dot{B}}_R \vert \Big ) S(t), \end{aligned}$$
(3.21)

As \(\varepsilon _N \rightarrow 0\) and \(\varepsilon _R \rightarrow 0\), thus

$$\begin{aligned} \liminf \limits _{t \rightarrow + \infty } S(t) \ge \dfrac{\Lambda }{d}. \end{aligned}$$
(3.22)

Also,

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } S(t) \le \dfrac{\Lambda }{d} + \varepsilon _N + \varepsilon _R. \end{aligned}$$
(3.23)

Let \(\varepsilon _N \rightarrow 0\) and \(\varepsilon _R \rightarrow 0\), one attain

$$\begin{aligned} \limsup \limits _{t \rightarrow + \infty } S(t) \le \dfrac{\Lambda }{d}. \end{aligned}$$
(3.24)

From (3.24) and (3.22), one get

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } S(t)= \dfrac{\Lambda }{d}. \end{aligned}$$
(3.25)

Next, we prove the last conclusion. Using the third equation of (1.2), we obtain

$$\begin{aligned} \mathrm {d} R(t) \ge ( \mu \varepsilon _N + \gamma \varepsilon _R -dR(t) ) \mathrm {d}t. \end{aligned}$$
(3.26)

Its clear by comparison theorem we deduce

$$\begin{aligned} \limsup \limits _{t \rightarrow + \infty } R(t)= \dfrac{ \mu \varepsilon _N + \gamma \varepsilon _R }{d}. \end{aligned}$$
(3.27)

Extending \(\varepsilon _N\) and \(\varepsilon _R\) to 0, we have

$$\begin{aligned} \lim \limits _{t \rightarrow + \infty } R(t)=0. \end{aligned}$$
(3.28)

\(\hfill\square\)

Remark 9

From Theorem 8 we show that the non-resistant and the resistant strains will die out if the white noise disturbances are large than certain values or \({\mathcal {R}}_N^s < 1\) and \({\mathcal {R}}_R^s < 1\), and the white noise disturbances are not so large.

4 Persistence in mean

In this section, our main concern to determine sufficient conditions for the persistence of the infectious disease.

Theorem 10

Let \({\mathbf {S}}(t)\) satisfies the model (1.2) with \({\mathbf {S}}_0\in \Gamma\),

  1. 1.

    If \({\mathcal {R}}_N^s > 1\), \({\mathcal {R}}_R^s <1\) and \(\sigma _R \le \sqrt{\dfrac{2 d \beta }{\Lambda }}\), then the resistance strain will go to extinct and the strain \(I_N\) will persist, furthermore, \(I_N\) satisfies

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) \rangle \ge \dfrac{d}{\alpha (d + \mu )}({\mathcal {R}}_N^s-1). \end{aligned}$$
  2. 2.

    If \({\mathcal {R}}_R^s > 1\), \({\mathcal {R}}_N^s < 1\) and \(\sigma _N \le \sqrt{\dfrac{2 d \alpha }{\Lambda }}\), then the non-resistance strain go to extinct and the strain \(I_R\) will persist, furthermore, \(I_R\) satisfies

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_R(t) \rangle \ge \dfrac{d}{\beta + d}({\mathcal {R}}_R^s-1). \end{aligned}$$
  3. 3.

    If \({\mathcal {R}}_N^s > 1\), \({\mathcal {R}}_R^s >1\), then the two strains \(I_N\) and \(I_R\) are persistent in mean, furthermore, \(I_N\) and \(I_R\) satisfy

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) + I_R(t) \rangle \ge \dfrac{1}{\varpi _{max}}\left[ (d+ \mu )( {\mathcal {R}}_N^s-1) + (d+ \gamma )( {\mathcal {R}}_R^s-1) \right] , \end{aligned}$$

where \(\varpi _{max} = \max \{ (\alpha + \beta )\dfrac{d+ \mu }{d}, (\dfrac{(\alpha + \beta )}{d}+1)(d + \gamma ) \}.\)

Proof

  1. 1.

    Let the function \(\Theta (t)\) define by \(\Theta (t)= S(t)+I_N(t)+I_R(t).\) Then the first three equation of model (1.2), implies

    $$\begin{aligned} \dfrac{\Theta (t)-\Theta (0)}{t} = \Lambda - d \langle S(t) \rangle - (d+ \mu ) \langle I_N(t) \rangle - (d+ \gamma ) \langle I_R(t) \rangle . \end{aligned}$$
    (4.1)

    Since \({\mathcal {R}}_R^s <1 ,\) and \(\sigma _R \le \sqrt{\dfrac{2 d \beta }{\Lambda }}\) one can see from Proposition 6 that, \(\limsup \limits _{t \rightarrow +\infty } I_R(t)=0\) almost surely. Then we can choose for all t large enough \(\varepsilon _R\) small enough, such that \(0< I_R(t) < \varepsilon _R ,\) therefore,

    $$\begin{aligned} \langle S(t) \rangle \ge \dfrac{\Lambda - (d+ \gamma ) \varepsilon _R}{d} - \dfrac{d+ \mu }{d} \langle I_N(t) \rangle - \dfrac{\Theta (t)}{d}. \end{aligned}$$
    (4.2)

    Using the Itô’s formula to model (1.2), we obtain

    $$\begin{aligned} \mathrm {d} \log I_N(t) = \Big ( \alpha S(t) -(d+ \mu ) - \dfrac{ \sigma _N^2 S^2(t)}{2} \Big ) \mathrm {d} t + \sigma _N S(t) \mathrm {d} B_N(t). \end{aligned}$$
    (4.3)

    Hence,

    $$\begin{aligned} \mathrm {d} \log I_N(t) \geqslant \Big ( \alpha S(t) -(d+ \mu ) - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2} \Big ) \mathrm {d} t + \sigma _N S(t) \mathrm {d} B_N(t). \end{aligned}$$
    (4.4)

    Integration of (4.4) gives

    $$\begin{aligned} \dfrac{\log I_N(t) - \log I_N(0) }{t}&\ge \alpha \langle S(t) \rangle - \Big [ d+ \mu + \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2} \Big ] + \dfrac{{\mathcal {M}}_N (t)}{t} \nonumber \\&\ge \alpha \Big [ \dfrac{\Lambda - (d+ \gamma ) \varepsilon _R}{d} - \dfrac{d+ \mu }{d} \langle I_N(t) \rangle - \dfrac{\Theta (t)}{d} \Big ] \nonumber \\&\quad - \Big [ d+ \mu + \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2} \Big ] + \dfrac{{\mathcal {M}}_N (t)}{t} \nonumber \\&= (d + \mu ) \Big [\dfrac{ \alpha [ \Lambda - (d+ \gamma ) \varepsilon _R ]}{d(d + \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2 (d + \mu )} -1 \Big ] - \dfrac{\alpha (d+ \mu )}{d} \langle I_N(t) \rangle + \dfrac{{\mathcal {M}}_N (t)}{t} -\alpha \dfrac{\Theta (t)}{d}. \end{aligned}$$
    (4.5)

    So, we obtain

    $$\begin{aligned} \dfrac{\log I_N(t)}{t}&\ge (d + \mu ) \Big [\dfrac{ \alpha [ \Lambda - (d+ \gamma ) \varepsilon _R ]}{d(d + \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2 (d + \mu )} -1 \Big ] - \dfrac{\alpha (d+ \mu )}{d} \langle I_N(t) \rangle \nonumber \\&\quad + \dfrac{{\mathcal {M}}_N (t)}{t} -\alpha \dfrac{\Theta (t)}{d} + \dfrac{\log I_N(0)}{t}, \end{aligned}$$
    (4.6)

    where \({\mathcal {M}}_N (t)= \displaystyle \int _{0}^{t} \sigma _N S(\zeta ) \, \mathrm {d} B_N(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_N (0)=0\), and using Lemma 4, the result is:

    $$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_N (t)}{t} = 0. \end{aligned}$$
    (4.7)

    Since \({\mathcal {R}}_N^s >1,\) for all t large enough we can choose \(\varepsilon _R\) small enough, such that

    $$\begin{aligned} \dfrac{ \alpha [ \Lambda - (d+ \gamma ) \varepsilon _R ]}{d(d + \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2 (d + \mu )} > 1. \end{aligned}$$

    By Lemmas 3 and 4, we get that

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) \rangle \ge \dfrac{d}{\alpha (d + \mu )} \bigg ( \dfrac{ \alpha [ \Lambda - (d+ \gamma ) \varepsilon _R ]}{d(d + \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2 (d + \mu )}-1 \bigg ). \end{aligned}$$

    Let \(\varepsilon _R \rightarrow 0\) yields

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) \rangle \ge \dfrac{d}{\alpha (d + \mu )} \bigg (\dfrac{ \alpha \Lambda }{d(d + \mu )} - \dfrac{ \sigma _N^2 \Lambda ^2}{2d^2 (d + \mu )}-1 \bigg ). \end{aligned}$$

    Therefore,

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) \rangle \ge \dfrac{d}{\alpha (d + \mu )}({\mathcal {R}}_N^s-1). \end{aligned}$$
  2. 2.

    Notice that

    $$\begin{aligned} \langle S(t) \rangle \ge \dfrac{\Lambda }{d} - \dfrac{(d + \mu )}{d} \varepsilon _N - \dfrac{(d + \gamma )}{d} \langle I_R(t) \rangle - \dfrac{ \Theta (t) }{d}. \end{aligned}$$
    (4.8)

    Applying the Itô’s formula leads to

    $$\begin{aligned} \mathrm {d} \left( \log I_R(t)+ I_R(t) \right)&= \left[ \beta S(t) - (d + \gamma ) - (d + \gamma ) I_R(t) - \dfrac{\sigma _R^2 S^2(t)}{2(1+ \kappa I_R(t))^2} \right] \mathrm {d} t + \sigma _R S(t) \mathrm {d} B_R(t) \nonumber \\&\ge \left[ \beta S(t) - (d + \gamma ) - (d + \gamma ) I_R(t) - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2} \right] \mathrm {d} t + \sigma _R S(t) \mathrm {d} B_R(t). \end{aligned}$$
    (4.9)

    Integration of (4.9) gives

    $$\begin{aligned} \dfrac{\log I_R(t) - \log I_R(0) }{t} + \dfrac{ I_R(t) - I_R(0) }{t}&\ge \beta \langle S(t) \rangle - (d + \gamma ) - (d + \gamma ) \langle I_R(t) \rangle \nonumber \\&\quad - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2} + \dfrac{{\mathcal {M}}_R (t)}{t} \nonumber \\&\ge \beta \left( \dfrac{\Lambda - (d + \mu ) \varepsilon _N }{d} \right) - (d + \gamma ) - (d + \gamma ) \langle I_R(t) \rangle \nonumber \\&\quad - \beta \dfrac{(d + \gamma )}{d} \langle I_R(t) \rangle - \beta \dfrac{ \Theta (t)}{d} + \dfrac{{\mathcal {M}}_R (t)}{t} \nonumber \\&= (d + \gamma ) \bigg [ \dfrac{\beta ( \Lambda - (d + \mu ) \varepsilon _N )}{d(d + \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2 (d + \gamma )} -1 \bigg ] \nonumber \\&\quad - \bigg [ \dfrac{\beta (d + \gamma ) }{d} + (d + \gamma ) \bigg ] \langle I_R(t) \rangle - \beta \dfrac{ \Theta (t)}{d} + \dfrac{{\mathcal {M}}_R (t)}{t}. \end{aligned}$$
    (4.10)

    Hence, we have

    $$\begin{aligned} \dfrac{\log I_R(t) }{t}&\ge (d + \gamma ) \bigg [ \dfrac{\beta ( \Lambda - (d + \mu ) \varepsilon _N )}{d(d + \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2 (d + \gamma )} -1 \bigg ] - \bigg [ \dfrac{\beta (d + \gamma ) }{d} + (d + \gamma ) \bigg ] \langle I_R(t) \rangle \nonumber \\&\quad - \beta \dfrac{ \Theta (t)}{d} + \dfrac{{\mathcal {M}}_R (t)}{t}- \dfrac{ I_R(t) - I_R(0) }{t} + \dfrac{ \log I_R(0) }{t}, \end{aligned}$$
    (4.11)

    where \({\mathcal {M}}_R (t)= \displaystyle \int _{0}^{t} \dfrac{ \sigma _R S(\zeta )}{1+\kappa I_R(\zeta )} \, \mathrm {d} B_R(\zeta )\) is the local continuous martingale satisfying \({\mathcal {M}}_R (0)=0\), and using Lemma 4, one have

    $$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_R (t)}{t} = 0. \end{aligned}$$
    (4.12)

    Since \({\mathcal {R}}_R^s >1,\) for all t large enough we can choose \(\varepsilon _N\) small enough, such that

    $$\begin{aligned} \dfrac{\beta ( \Lambda - (d + \mu ) \varepsilon _N )}{d(d + \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2 (d + \gamma )} > 1, \end{aligned}$$

    By Lemmas 3 and 4, we get that

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_R(t) \rangle \ge \dfrac{d}{\beta + d} \bigg ( \dfrac{\beta ( \Lambda - (d + \mu ) \varepsilon _N )}{d(d + \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2 (d + \gamma )}-1 \bigg ), \end{aligned}$$

    Let \(\varepsilon _N \rightarrow 0\) yields

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_R(t) \rangle \ge \dfrac{d}{\beta + d} \bigg ( \dfrac{\beta \Lambda }{d(d + \gamma )} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2 (d + \gamma )}-1 \bigg ). \end{aligned}$$

    Therefore

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_R(t) \rangle \ge \dfrac{d}{\beta + d} \bigg ( {\mathcal {R}}_R^s-1 \bigg ). \end{aligned}$$
  3. 3.

    Notice that

    $$\begin{aligned} \langle S(t) \rangle = \dfrac{\Lambda }{d} - \dfrac{(d + \mu )}{d} \langle I_N(t) \rangle - \dfrac{(d + \gamma )}{d} \langle I_R(t) \rangle - \dfrac{ \Theta (t) }{d}. \end{aligned}$$
    (4.13)

    Define

    $$\begin{aligned} \vartheta (t) = \log (I_N(t)) + \log (I_R(t)) + I_R(t). \end{aligned}$$
    (4.14)

    With the help of Itô’s formula, we reach:

    $$\begin{aligned} \mathrm {d} \vartheta (t)=& \Big ( \alpha S(t) + \beta S(t) - (d+ \mu ) - (d + \gamma )(1+ I_R(t)) - \dfrac{\sigma _N^2}{2} S^2(t) - \dfrac{\sigma _R^2 S^2(t)}{2(1+ \kappa I_R(t))^2} \Big ) \mathrm {d} t \nonumber \\&\quad + \sigma _N S(t) \mathrm {d} B_N(t) + \sigma _R S(t) \mathrm {d} B_R(t). \end{aligned}$$
    (4.15)

    Therefore

    $$\begin{aligned} \mathrm {d} \vartheta (t)&\ge (\alpha + \beta )S(t) - (d+ \mu ) - \dfrac{\sigma _N^2 \Lambda ^2}{2 d^2} + \sigma _N S(t) \mathrm {d} B_N(t) \nonumber \\&\quad - (d + \gamma )(1+ I_R(t)) - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2} + \sigma _R S(t) \mathrm {d} B_R(t). \end{aligned}$$
    (4.16)

    Integration of (4.16) gives

    $$\begin{aligned} \dfrac{\vartheta (t)}{t} - \dfrac{\vartheta (0)}{t}&\ge (\alpha + \beta ) \langle S(t) \rangle - (d+ \mu ) - (d+ \gamma ) - \dfrac{\sigma _N^2 \Lambda ^2}{2d^2} + \dfrac{{\mathcal {M}}_N (t)}{t} \nonumber \\&\quad - (d + \gamma )\langle I_R(t) \rangle - \dfrac{\sigma _R^2 \Lambda ^2}{2 d^2} + \dfrac{{\mathcal {M}}_R (t)}{t} \nonumber \\&= (\alpha + \beta ) \dfrac{\Lambda }{d} - (d+ \mu ) - (d+ \gamma ) - \dfrac{\sigma _N^2 \Lambda ^2}{2 d^2} + \dfrac{{\mathcal {M}}_N (t)}{t} - (\alpha + \beta )\dfrac{d+ \mu }{d} \langle I_N(t) \rangle \nonumber \\&\quad - \left(\dfrac{(\alpha + \beta )}{d}+1\right)(d + \gamma )\langle I_R(t) \rangle - \dfrac{\sigma _R^2 \Lambda ^2}{2 d^2} + \dfrac{{\mathcal {M}}_R (t)}{t} - ( \alpha + \beta ) \dfrac{ \Theta (t)}{d}\nonumber \\&\ge ( \alpha + \beta ) \dfrac{\Lambda }{d} - (d+ \mu ) - (d+ \gamma )- \dfrac{\sigma _N^2 \Lambda ^2}{2 d^2} - \dfrac{\sigma _R^2 \Lambda ^2}{2d^2} \nonumber \\&\quad - \varpi _{max} \bigg [ \langle I_N(t) \rangle + \langle I_R(t) \rangle \bigg ] - ( \alpha + \beta ) \dfrac{ \Theta (t)}{d} + \dfrac{{\mathcal {M}}_N (t)}{t} + \dfrac{{\mathcal {M}}_R (t)}{t}. \end{aligned}$$
    (4.17)

    Hence, the result becomes

    $$\begin{aligned} \langle I_N(t) \rangle + \langle I_R(t) \rangle&\ge \dfrac{1}{\varpi _{max}} \bigg [ (\alpha + \beta ) \dfrac{\Lambda }{d} - (d+ \mu ) - (d+ \gamma ) - \dfrac{\sigma _N^2 \Lambda ^2}{2d^2} - \dfrac{\sigma _R^2 \Lambda ^2}{2 d^2} \nonumber \\&\quad - ( \alpha + \beta ) \dfrac{ \Theta (t)}{d} + \dfrac{{\mathcal {M}}_N (t)}{t} + \dfrac{{\mathcal {M}}_R (t)}{t} - \dfrac{\vartheta (t)}{t}+ \dfrac{\vartheta (0)}{t} \bigg ], \end{aligned}$$
    (4.18)

    where \({\mathcal {M}}_N (t)= \displaystyle \int _{0}^{t} \sigma _N S(\zeta ) \, \mathrm {d} B_N(\zeta )\) and \({\mathcal {M}}_R (t)= \displaystyle \int _{0}^{t} \dfrac{ \sigma _R S(\zeta )}{1+\kappa I_R(\zeta )} \, \mathrm {d} B_R(\zeta )\) which are local continuous martingales satisfying \({\mathcal {M}}_N (0)=0\) and \({\mathcal {M}}_R (0)=0\), and by lemma 4, we have

    $$\begin{aligned} \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_N (t)}{t} = \lim \limits _{t \rightarrow + \infty } \dfrac{{\mathcal {M}}_R (t)}{t} = 0. \end{aligned}$$
    (4.19)

    From Lemmas 3 and 4, we get that

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) + I_R(t) \rangle \ge \dfrac{1}{\varpi _{max}}\bigg [(\alpha + \beta ) \dfrac{\Lambda }{d} - (d+ \mu ) - (d+ \gamma ) - \dfrac{\sigma _N^2 \Lambda ^2}{2d^2} - \dfrac{\sigma _R^2 \Lambda ^2}{2 d^2} \bigg ]. \end{aligned}$$

    Hence

    $$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \langle I_N(t) + I_R(t) \rangle \ge \dfrac{1}{\varpi _{max}}\bigg [ (d+ \mu )( {\mathcal {R}}_N^s-1) + (d+ \gamma )( {\mathcal {R}}_R^s-1) \bigg ] >0. \end{aligned}$$

    This is completes the proofs.

\(\hfill\square\)

Remark 11

Proposition 5 and Proposition 6 shows that the non-resistance and the resistance infections diseases can be extinct if the white noise disturbances are larger than certain values. Theorem 8 and 10 show that the non-resistant (resistant) infection diseases can prevail if the white noise disturbances are small enough such that \({\mathcal {R}}_N^s > 1\) ( \({\mathcal {R}}_R^s > 1\) ) respectively. This implies that the stochastic disturbance may cause epidemic diseases to die out.

5 Graphical analysis

In this section, we implement the Milstein procedure which is given in [43] to test numerically the persistence and the extinction of the disease. The discretization of system 1.2 is given by

$$\begin{aligned} \left\{ \begin{array}{llll} \displaystyle S_{j+1}&=S_j + \bigg [ \Lambda - \alpha S_j I_{Nj} - \dfrac{\beta S_j I_{Rj}}{1+\kappa I_{Rj}}-d S_j \bigg ] \Delta t - \sigma _N S_j I_{Nj} \sqrt{ \Delta t} \xi _j -\dfrac{\sigma _R S_j I_{Rj}}{1+\kappa I_{Rj}} \sqrt{\Delta t} \xi _j \\ & \quad\quad + \dfrac{\sigma _N^2}{2} S_j^2 I_{Nj} ^2 (\xi _j^2-1) \Delta t + \dfrac{\sigma _R^2}{2}\bigg (\dfrac{\beta S_j I_{Rj}}{1+\kappa I_{Rj}} \bigg ) ^2 ( \xi _j^2-1) \Delta t ,\\ \\ \displaystyle I_{Nj+1} &=I_{Nj} + \bigg ( \alpha S_j I_{Nj} - (d + \mu ) I_{Nj} \bigg ) \Delta t + \sigma _N S_j I_{Nj} \sqrt{\Delta t} \xi _j + \dfrac{\sigma _N^2}{2} S_j^2 I_{Nj}^2(\xi _j^2-1) \Delta t ,\\ \\ \displaystyle I_{Rj+1}& =I_{Rj} + \bigg ( \dfrac{\beta S_j I_{Rj}}{1+\kappa I_{Rj}}-(d + \gamma )I_{Rj} \bigg ) \Delta t+\dfrac{\sigma _R S_j I_{Rj}}{1+\kappa I_{Rj}} \sqrt{\Delta t} \xi _j + \dfrac{\sigma _R^2}{2} \bigg (\dfrac{\beta S_j I_{Rj}}{1+\kappa I_{Rj}} \bigg )^2(\xi _j^2-1) \Delta t ,\\ \\ \displaystyle R_{j+1} &=R_{j} + \bigg ( \mu I_{Nj} + \gamma I_{Rj} -d R_j \bigg )\Delta t, \end{array} \right. \end{aligned}$$
(5.1)

where \(\xi _k,\) \((j=1,2,...,n)\) are the Guassian random variables which Obey Gaussian distribution \({\mathcal {N}}(0;1)\).

Indeed, Fig. 2 shows the dynamics of the non-resistance and resistance strains of influenza for the chosen values of the parameters \(\Lambda =10\), \(\alpha =0.08\), \(\beta =0.09\), \(d=0.5\), \(\mu =0.5\), \(\kappa =0.04\), \(\gamma =0.5\), \(\sigma _N= 0.01\) and \(\sigma _R= 0.01\). We clearly see that the all the model variables stay at a strictly positive level. Within this parameters, we have \({\mathcal {R}}_N^s =1.58 >1\) and \({\mathcal {R}}_R^s =1.78 >1\), then the two infectious diseases \(I_N\) and \(I_R\) will persist. This result is consistent with the theoretical result given in Theorem 10.

Fig. 2
figure 2

Dynamic describing the persistence of the non-resistance and resistance diseases

Full size image

Next, we take the parameters values for the stochastic model 1.2 as: \(\Lambda =10\), \(\alpha =0.03\), \(\beta = 0.09\), \(d=0.3\), \(\mu =0.7\), \(\kappa =0.4\), \(\sigma _N=0.01\) and \(\sigma _R=0.01\). Within this parameters we get \({\mathcal {R}}_N^s =0.9444<1\) and \({\mathcal {R}}_R^s =2.9306 >1\), \(\sigma _N =10^{-4}\le \sqrt{\dfrac{2 d\alpha }{\Lambda }}=0.0018\). Thus, non-resistance strain \(I_N\) goes to the extinction, and resistance strain \(I_R\) will persist (see Fig. 3). This result is consistent with the theoretical result given in Theorem 10.

Fig. 3
figure 3

Dynamic describing the persistence of the non-resistance strain and the extinction of resistance strain

Full size image

In Fig. 4, we take the parameters values for the model 1.2 as: \(\Lambda =10\), \(\alpha =0.09\), \(\beta = 0.03\), \(d=0.3\), \(\mu =0.7\),\(\gamma =0.9\), \(\kappa =0.4\), \(\sigma _N=0.01\) and \(\sigma _R=0.01\). Within this parameters we get \({\mathcal {R}}_N^s =2.9444>1\), \({\mathcal {R}}_R^s =0.9537 <1\) and \(\sigma _R =10^{-4}\le \sqrt{\dfrac{2d\beta }{\Lambda }}=0.0018\). Thus, non-resistance strain \(I_N\) is persistent, and resistance strain \(I_R\) go to extinction.

Fig. 4
figure 4

Dynamics of the infection describing the persistence of the non-resistance strain and the extinction of resistance strain

Full size image

In Fig. 5, we take the parameters values for the model 1.2 as: \(\Lambda =10\), \(\alpha =0.03\), \(\beta = 0.03\), \(d=0.3\), \(\mu =0.7\), \(\gamma =0.9\), \(\kappa =0.4\), \(\sigma _N=0.01\) and \(\sigma _R=0.01\). Within this parameters we get \({\mathcal {R}}_N^s =0.9444<1\), \({\mathcal {R}}_R^s =0.9537 <1\) and both conditions \(\sigma _N = 0.01 \le \sqrt{\dfrac{2d \alpha }{\Lambda }} = 0.1341\) and \(\sigma _R = 0.01 \le \sqrt{\dfrac{2d \beta }{\Lambda }} = 0.1341\). Thus, both of them go to the extinction which is consistent with the theoretical result given in Sect. 3.

Fig. 5
figure 5

Dynamics of the infection describing the persistence of the non-resistance strain and the extinction of resistance strain

Full size image

6 Conclusion and discussion

The novelty of this study is that we analyzed the dynamics of two-strain SIR epidemic model including non-resistance and resistance sub-strain of influenza, by considering different incidence rates for these strains. This is due to the fact that the mutated strain will have a minimal effect. We have assumed saturated and bilinear incidence rates for the resistant and non-resistant strains respectively. Saturated incidence rate grasps the negotiating alteration and swarming impact of the infected people and hinders the unboundedness of the interconnection rate by fitting parameters, which was reused in several epidemic issue . Indeed, a stochastic two-strain epidemic model describing resistance and non-resistance strains of influenza was suggested and studied. The existence and uniqueness of the positive solution to the stochastic model (1.2) are proved. The extinction of our studied disease was derived with sufficient conditions. The persistence in the mean of the infection was also established. Different numerical simulations for different noises disturbance were performed to illustrate the efficiency of our theoretical study.

Some interesting topics deserve further investigation. On the one hand, one may propose some more realistic models, such as considering the effects of impulsive perturbations on system (1.2). On the other hand, it is interesting to introduce the telegraph noise, such as continuous-time Markov chain, into system (1.2). Also it is interesting to consider more complex influenza virus models, for example, multi-group model. These problems will be the subject of future work.