Nonintegrable threshold singularities of two-point functions in perturbation theory

Abstract

In perturbation theory, the spectral densities of two-point functions develop nonintegrable threshold singularities at higher orders. In QCD, such singularities emerge when calculating the diagrams in terms of the pole quark mass, and they become stronger when one rearranges the perturbative expansion in terms of the running quark mass. In this paper, we discuss the proper way to handle such singularities.

Appendices

Appendix A: Proof by induction for $F_{n+\frac{1}{2}}$ [odd powers $1/v^{2n+1}$]

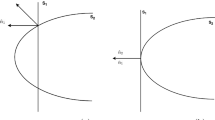
We start with the integral over the cut

$$\begin{aligned} F_{n+\frac{1}{2}}(z,\epsilon )= \frac{z}{\pi }\int _{1 + \epsilon }^\infty \mathrm{d}z' \frac{1}{(1- \frac{1}{z'})^{n+\frac{1}{2}}} \frac{1}{z'(z'-z)}. \end{aligned}$$

(A.1)

By virtue of (2.6), we come to a recursive relation

$$\begin{aligned} F_{n+\frac{1}{2}}(z,\epsilon )= \frac{z}{z-1} F_{n-\frac{1}{2}}(z,\epsilon ) + \frac{1}{\pi }\frac{z}{1 - z}\Delta F_{n+\frac{1}{2}}(\epsilon ), \end{aligned}$$

(A.2)

where

$$\begin{aligned} \Delta F_{n+\frac{1}{2}}(\epsilon )= & {} \int _{1 + \epsilon }^\infty \mathrm{d}z' \frac{1}{(1- \frac{1}{z'})^{n+\frac{1}{2}}} \frac{1}{z'^2}\nonumber \\= & {} \frac{\left( \frac{\epsilon }{1+\epsilon }\right) ^{\frac{1}{2}-n}-1}{n-\frac{1}{2}}. \end{aligned}$$

(A.3)

This function is represented by an infinite sum of powers of $\sqrt{\epsilon }$, the most singular term being of the order ${\epsilon }^{-(n-\frac{1}{2})}$. Noteworthy, the $\epsilon$-independent term in $\Delta F_{n+\frac{1}{2}}(\epsilon )$ is

$$\begin{aligned} -\frac{1}{(n-\frac{1}{2})}. \end{aligned}$$

(A.4)

We now conjecture that the $\epsilon$-independent part of the recursive relation (A.2) yields the recursive relation for $F_{n+\frac{1}{2}}(z)$:

$$\begin{aligned} F_{n+\frac{1}{2}}(z)-F_{n+\frac{1}{2}}(0)= & {} \frac{z}{z-1}\left\{ F_{n-\frac{1}{2}}(z)-F_{n-\frac{1}{2}}(0)\frac{}{}\right\} \nonumber \\&+\frac{1}{\pi }\frac{z}{z-1} \frac{1}{(n-\frac{1}{2})},\quad n\ge 1, \end{aligned}$$

(A.5)

where the knowledge of the $\epsilon$-independent term in $\Delta F_{n+\frac{1}{2}}(\epsilon )$ is used.

The analytic solution $F_{\frac{1}{2}}(z)$ is easily found:

$$\begin{aligned} F_{\frac{1}{2}}(z)=F_{\frac{1}{2}}(0) -\frac{2}{\pi }\sqrt{\frac{z}{z-1}}\log \left( \sqrt{-z}+\sqrt{1-z}\right) . \end{aligned}$$

(A.6)

Solving (A.5) iteratively, we find the conjectured solution $F_{n+\frac{1}{2}}(z)$. We still have to prove that this function indeed satisfies the integral equation (2.4). To this end, we need to calculate the small-circle integral of the function $F_{n+\frac{1}{2}}(z)$, see Eq. (2.4).

Using (2.6), the small-circle integral satisfies a recursive relation similar to (A.2):

$$\begin{aligned} I_{n+\frac{1}{2}}(z,\epsilon )= & {} \frac{z}{z-1} I_{n-\frac{1}{2}}(z,\epsilon ) + \frac{1}{\pi }\frac{z}{1 - z}\Delta I_{n+\frac{1}{2}}(\epsilon ), \end{aligned}$$

(A.7)

where

$$\begin{aligned} \Delta I_{n+\frac{1}{2}}(\epsilon )= & {} \frac{1}{2\pi i}\oint _{1 + \epsilon } \mathrm{d}z' F_{n+\frac{1}{2}}(z')\frac{1}{z'^2}. \end{aligned}$$

(A.8)

To calculate this small-circle integral, we expand the integrand near $z=1$. Making use of the expansion

$$\begin{aligned} F_{n+\frac{1}{2}}(z)= & {} (-1)^n\left( \frac{z}{1-z}\right) ^{n+\frac{1}{2}}+O((z-1)^0) \end{aligned}$$

(A.9)

and expanding also $1/z^2$ near $z=1$, we find

$$\begin{aligned} \Delta F_{n+\frac{1}{2}}(\epsilon )+\Delta I_{n+\frac{1}{2}}(\epsilon )=-\frac{1}{(n-\frac{1}{2})}, \end{aligned}$$

(A.10)

yielding

$$\begin{aligned}&F_{n+\frac{1}{2}}(z,\epsilon )+I_{n+\frac{1}{2}}(z,\epsilon )\nonumber \\&\quad =\frac{z}{z-1}\left\{ F_{n-\frac{1}{2}}(z,\epsilon )+I_{n-\frac{1}{2}}(z,\epsilon ) \right\} \nonumber \\&\qquad +\frac{z}{\pi (z-1)}\frac{1}{(n-\frac{1}{2})}. \end{aligned}$$

(A.11)

This equation coincides with Eq. (A.5) for

$$\begin{aligned} F_{n+\frac{1}{2}}(z)-F_{n+\frac{1}{2}}(0) =F_{n+\frac{1}{2}}(z,\epsilon )+I_{n+\frac{1}{2}}(z,\epsilon ) \end{aligned}$$

(A.12)

and verifies by induction that the sum $F_{n+\frac{1}{2}}(z,\epsilon )+I_{n+\frac{1}{2}}(z,\epsilon )$ does not depend on $\epsilon$ (since $F_{\frac{1}{2}}(z)-F_{\frac{1}{2}}(0)$ is $\epsilon$-independent). We therefore prove our conjecture that the solution $F_{n+\frac{1}{2}}(z)$ is obtained from the dispersion integral over the cut, $F_{n+\frac{1}{2}}(z,\epsilon )$, by omitting all $\epsilon$-dependent terms. Let us emphasize that the only role of the small-circle integral $I_{n+\frac{1}{2}}(z,\epsilon )$ is to cancel the $\epsilon$-dependent terms in $F_{n+\frac{1}{2}}(z,\epsilon )$; it leaves no other traces.

Appendix B: Proof by induction for $F_n$ [even powers $1/v^{2n}$]

This appendix gives the analysis for the case $F_{n}$ which has some subtleties compared to the analysis for $F_{n+\frac{1}{2}}$ of Appendix A.

We start with the integral over the cut

$$\begin{aligned} F_n(z,\epsilon )= \frac{z}{\pi }\int _{1 + \epsilon }^\infty \mathrm{d}z' \frac{1}{(1- \frac{1}{z'})^n} \frac{1}{z'(z'-z)}. \end{aligned}$$

(B.1)

By virtue of (2.6), one obtains a recursive relation

$$\begin{aligned} F_n(z,\epsilon )= \frac{z}{z-1} F_{n-1}(z,\epsilon )+ \frac{1}{\pi }\frac{z}{1 - z}\Delta F_n(\epsilon ), \end{aligned}$$

(B.2)

where

$$\begin{aligned} \Delta F_n(\epsilon )= & {} \int _{1 + \epsilon }^\infty \mathrm{d}z' \frac{1}{(1- \frac{1}{z'})^n} \frac{1}{z'^2}\nonumber \\= & {} \frac{ \left[ (1 + \frac{1}{\epsilon })^n - 1\right] \epsilon - 1}{(n-1)(1 + \epsilon )}. \end{aligned}$$

(B.3)

For integer n, this function is represented by a finite sum of poles in $1/\epsilon$ of the increasing order; it contains no regular structures in $\epsilon$.

Solving (B.2) for the $\epsilon$-independent part and making use of the known expression for $F_1(z)$, we obtained $F_n(z)$ in the form [see (2.21)]:

$$\begin{aligned} F_n(z)=F_n(0) - \frac{1}{\pi } \left( \frac{z}{z - 1} \right) ^n \log (1-z). \end{aligned}$$

(B.4)

This is still our conjecture and we have to check that this function satisfies the integral equation (2.4).

Let us calculate the small-circle integral for $F_n(z)$ given by (B.4). Using again (2.6), we obtain also for the small-circle integral a recursive relation

$$\begin{aligned} I_n(z,\epsilon )= & {} \frac{z}{z-1} I_{n-1}(z,\epsilon )+ \frac{1}{\pi } \frac{z}{1 - z}\Delta I_n(\epsilon ), \end{aligned}$$

(B.5)

where

$$\begin{aligned} \Delta I_n(\epsilon )= & {} \frac{1}{2\pi i}\oint _{1 + \epsilon } \mathrm{d}z'\log (1-z') \frac{1}{(1- \frac{1}{z'})^n} \frac{1}{z'^2}\nonumber \\= & {} -\frac{ \left[ (1 + \frac{1}{\epsilon })^n - 1\right] \epsilon - 1}{(n-1)(1 + \epsilon )}=-\Delta F_n(\epsilon ), \end{aligned}$$

(B.6)

Thus, $F_n(z,\epsilon )+I_n(z,\epsilon )$ satisfies the recursive relation

$$\begin{aligned} F_n(z,\epsilon )+I_n(z,\epsilon )=\frac{z}{z-1}\left\{ F_{n-1}(z,\epsilon ) +I_{n-1}(z,\epsilon ) \frac{}{}\right\} . \end{aligned}$$

(B.7)

For $n=1$ we find

$$\begin{aligned} F_1(z,\epsilon )= & {} -\frac{1}{\pi } \frac{z}{z-1}\log (1-z) +\frac{1}{\pi } \frac{z}{z-1} \log (\epsilon )\nonumber \\&+\frac{z}{(z-1)^2}\epsilon +\frac{z}{2(z-1)^3}\epsilon ^2+O(\epsilon ^3) \end{aligned}$$

(B.8)

and

$$\begin{aligned} I_1(z,\epsilon )= & {} -\frac{1}{\pi } \frac{z}{z-1} \log (\epsilon )\nonumber \\&-\frac{z}{(z-1)^2}\epsilon -\frac{z}{2(z-1)^3}\epsilon ^2+O(\epsilon ^3), \end{aligned}$$

(B.9)

leading to

$$\begin{aligned} F_1(z,\epsilon )+I_1(z,\epsilon )=-\frac{1}{\pi }\frac{z}{z-1}\log (1-z). \end{aligned}$$

(B.10)

Let us emphasize again that not only singular in $\epsilon$ terms, but also powers of $\epsilon$ cancel in the sum, so $F_1(z,\epsilon )+I_1(z,\epsilon )$ does not depend on $\epsilon$ at all. As follows from (B.7), for any n the sum $F_n(z,\epsilon )+I_n(z,\epsilon )$ also does not depend on $\epsilon$ and has the form

$$\begin{aligned} F_n(z,\epsilon )+I_n(z,\epsilon )=-\frac{1}{\pi }\left( \frac{z}{z-1}\right) ^n\log (1-z). \end{aligned}$$

(B.11)

So our conjectured solution (B.4) indeed solves the integral equation (2.4).