Transverse dynamics of vector solitons in defocusing nonlocal media

Abstract

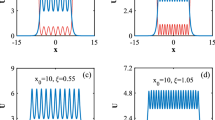
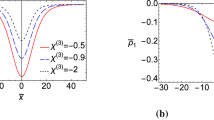
The transverse instability of line solitons of a multicomponent nonlocal defocusing nonlinear Schrödinger (NLS) system is utilized to construct lump and vortex-like structures in 2D nonlocal media, such as nematic liquid crystals. These line solitons are found by means of a perturbation expansion technique, which reduces the nonintegrable vector NLS model to a completely integrable scalar one, namely to a Kadomtsev–Petviashvili equation. It is shown that dark or antidark soliton stripes, as well as dark lumps, are possible depending on the strength of nonlocality: dark (antidark) solitons are formed for weaker (stronger) nonlocality, relatively to a threshold that is analytically determined in terms of the parameters of the system and the continuous-wave amplitude. Direct numerical simulations are used to show that dark lump-like- and vortex-like-structures can spontaneously be formed as a result of the transverse instability of the dark soliton stripes.

Appendix: Derivation of the KP equation

Here, we provide details on the perturbation expansion and the derivation of the KP equation. First, Eq. (12a) yields:

$$\begin{aligned} O(\varepsilon ^{3/2})&: \quad -c\rho _{1X} + d_1 \rho _0 \phi _{1XX} =0, \end{aligned}$$

(33)

$$\begin{aligned} O(\varepsilon ^{5/2})&: \quad \rho _{1T}-c \rho _{2X}+d_1\left[ \left( \rho _1\phi _{1X}\right) _X +\rho _0\phi _{1YY}+\rho _0\phi _{2XX}\right] =0. \end{aligned}$$

(34)

From Eq. (12b), we obtain:

$$\begin{aligned} O(\varepsilon )&:\quad -c\phi _{1X}+2g_1\theta _1=0, \end{aligned}$$

(35)

$$\begin{aligned} O(\varepsilon ^2)&:\quad \phi _{1T}-c\phi _{2X}+2g_1\theta _2+\frac{d_1}{2} \left( \phi _{1X}^2-\frac{1}{2\rho _0}\rho _{1XX}\right) =0. \end{aligned}$$

(36)

Equation (12c) yields:

$$\begin{aligned} O(\varepsilon ^{3/2})&: \quad -c\sigma _{1X} + d_2 \sigma _0 \psi _{1XX} =0, \end{aligned}$$

(37)

$$\begin{aligned} O(\varepsilon ^{5/2})&: \quad \sigma _{1T}-c \sigma _{2X}+d_2\left[ \left( \sigma _1\psi _{1X}\right) _X +\sigma _0\phi _{1YY}+\sigma _0\psi _{2XX}\right] =0. \end{aligned}$$

(38)

From Eq. (12d), we obtain:

$$\begin{aligned} O(\varepsilon )&:\quad -c\psi _{1X}+2g_2\theta _1=0, \end{aligned}$$

(39)

$$\begin{aligned} O(\varepsilon ^2)&:\quad \psi _{1T}-c\psi _{2X}+2g_2\theta _2+\frac{d_2}{2} \left( \psi _{1X}^2-\frac{1}{2\sigma _0}\sigma _{1XX}\right) =0, \end{aligned}$$

(40)

and, finally, Eq. (12e) leads to:

$$\begin{aligned} O(\varepsilon )&:\quad -q\theta _1+g_1\rho _1+g_2\sigma _1=0, \end{aligned}$$

(41)

$$\begin{aligned} O(\varepsilon ^2)&:\quad \nu \theta _{1XX}-2q\theta _2+2(g_1\rho _2+g_2\sigma _2)=0. \end{aligned}$$

(42)

We consider the linear equations (33), (35), (37), (39) and (41). This system can be simplified as follows: differentiate Eqs. (35) and (39) with respect to X, and substitute $\theta _1$ from Eq. (41), $\phi _{1XX}$ from Eq. (33) and $\psi _{1XX}$ from Eq. (37). This yields the following two equations:

$$\begin{aligned}&\left( -\frac{c^2}{d_1\rho _0}+\frac{2g_1^2}{q} \right) \rho _{1X}+ \frac{2g_1g_2}{q}\sigma _{1X}=0, \end{aligned}$$

(43)

$$\begin{aligned}&\frac{2g_1g_2}{q}\rho _{1X} + \left( -\frac{c^2}{d_2\sigma _0}+\frac{2g_2^2}{q} \right) \sigma _{1X}=0. \end{aligned}$$

(44)

The above system for the unknown functions $\rho _{1X}$ and $\sigma _{1X}$ has nontrivial solutions as long as the determinant of the coefficients is equal to zero. This requirement leads to the speed of sound, given in Eq. (15).

Next, we proceed with the equations at the next order of approximation, namely with Eqs. (34), (36), (38), (40) and (42). First, multiply (36) by $\frac{d_1\rho _0}{c}$ and (40) by $\frac{d_2\sigma _0}{c}$, respectively, and differentiate them with respect to X. Then, adding the resulting equations with (34) and (38), respectively, we obtain the following system of equations:

$$\begin{aligned}&-c\rho _{2X}+ \rho _{1T}+ d_1(\rho _1\phi _{1X})_{X}+d_1\rho _0\phi _{1YY} +\frac{d_1\rho _0}{c}\phi _{1TX}+\frac{2d_1g_1\rho _0}{c}\theta _{2X}\nonumber \\&\quad +\,\frac{d_1^2\rho _0}{2c}(\phi _{1X})^2_{X}-\frac{d_1^2}{4c}\rho _{1XXX}=0, \end{aligned}$$

(45)

$$\begin{aligned}&-\,c\sigma _{2X}+ \sigma _{1T}+ d_2(\sigma _1\psi _{1X})_{X}+d_2\sigma _0\psi _{1YY} +\frac{d_2\sigma _0}{c}\psi _{1TX}+\frac{2d_2g_2\sigma _0}{c}\theta _{2X}\nonumber \\&\quad +\,\frac{d_2^2\sigma _0}{2c}(\psi _{1X})^2_{X}-\frac{d_2^2}{4c}\sigma _{1XXX}=0, \end{aligned}$$

(46)

$$\begin{aligned}&\nu \theta _{1XX}-2q\theta _2+2(g_1\rho _2+g_2\sigma _2)=0. \end{aligned}$$

(47)

This system can be further simplified as follows. Multiply Eqs. (45) and (46) by $-\frac{g_1}{qc}$ and $-\frac{g_2}{qc}$, respectively, and add the resulting equations. Then, substituting $\theta _2$ from Eq. (47), and using Eqs. (33), (37) and (43), we derive the KP equation (19).