1 Introduction

Compact objects play a crucial role in recent astrophysics, as they directly demonstrate the most interesting effects of general relativity. The most relevant astrophysical compact objects are surely black holes, both stellar mass and supermassive, at least from the point of view of the studies of the strong gravity phenomena, related e.g. to the existence of the unstable photon spheres. In the analysis of gravitational waves detected because of merging black holes, their mimickers, or neutron stars [1], quasinormal modes of gravitational waves (or related electromagnetic waves) created during the merging are related to the unstable circular null geodesics, as demonstrated in [2], if models based on the Einstein gravity are assumed; however, this is not necessarily true in alternative gravity theories [3] and exceptions can occur also in the Einstein theory combined with a non-linear electrodynamics [4,5,6].

Interesting phenomena could be related also to the stable photon spheres whose existence is possible in the vacuum Kerr naked singularity space-times, or Kerr superspinars [7, 8] related to the Kerr black holes [9, 10]. Of special interest are non-vacuum extremely compact objects allowing for the existence of stable photon spheres that could be relevant for the description of extremely compact neutron stars [11, 12]. The extremely compact objects contain a region of trapped null geodesics, allowing for trapping of gravitational waves [13], gravitational collapse [14], or trapping of neutrinos [15].

Recent studies indicate that the Tolman VII space-time with energy density radial profile of quadratic character [16], being an exact solution of the non-vacuum Einstein gravitational equations, can well represent neutron stars with realistic equations of state [17,18,19,20,21,22], contrary to the famous internal Schwarzschild solution governed by uniform distribution of energy in the interior [23, 24] representing the polytrope solution with polytropic index \(n=0\) [12, 25]. An anisotropic version of the Tolman VII solution was presented in [26].Footnote 1 In the same direction, it has been studied the rotation influence on the trapping effect in the case of linearized Hartle-Thorne space-times based on the Tolman VII spherically symmetric solutions, where was demonstrated enhancement (suppression) of the trapping effect in the case of counter-rotating (co-rotating) null geodesics due to the behavior of the effective potentials and escape cones of the null geodesics [28]. Given this result, it should be interesting to explore how other modifications of Tolman VII solution have an impact on the trapping effect and, among all the possibilities, in this work we are interested in modifications based on its interaction with a fluid satisfying a polytropic equation of state.

In the framework of general relativity, we can always group fluids of different nature into a single energy–momentum tensor

$$\begin{aligned} {\tilde{T}}_{\mu \nu }=T_{\mu \nu }^{1}+T_{\mu \nu }^{2}+\cdots \end{aligned}$$
(1)

However, extracting the information on which source dominates over the others, and consequently rule out any equation of state incompatible with the dominant source should be a difficult task. However, in a recent paper [29], we found a systematic way to explore the effect that a polytropic fluid has on an arbitrary source regardless its nature through the gravitational decoupling (GD) [30] in spherically symmetric space-times based on the minimal geometric deformation (MGD) [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] in its extended form [49] (for an incomplete list of references, see [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91]. See also Ref. [92], for the axially symmetric case). In this work, we shall follow Ref. [29] to study the effect of a polytrope on the Tolman VII geometry.

The paper is organized as follows: in Sect. 2, we first review the fundamentals of the GD approach to a spherically symmetric system containing two generic sources; in Sect. 3, we choose a polytropic fluid to study its effects on a generic gravitational source, and we introduce a systematic and direct procedure to elucidate these effects; in Sect. 4, we implement the strategy developed in Sect. 3 for the case of a perfect fluid; finally, we summarize our conclusions in Sect. 5.

2 Gravitational decoupling

In this section, we briefly review the GD for spherically symmetric gravitational systems (see [49] for details). Let us consider the Einstein field equationsFootnote 2

$$\begin{aligned} G_{\mu \nu } \equiv R_{\mu \nu }-\frac{1}{2}\,R\, g_{\mu \nu } = \kappa \,\,{\tilde{T}}_{\mu \nu } \ , \end{aligned}$$
(2)

where,

$$\begin{aligned} {\tilde{T}}_{\mu \nu } = T^\mathrm{}_{\mu \nu } + \theta _{\mu \nu } \ , \end{aligned}$$
(3)

with \(T_{\mu \nu }\) representing the source of some known solution and \(\theta _{\mu \nu }\) being an extra source containing new fields (or a new gravitational sector not described by general relativity). Note that, Bianchi identities lead to conservation of the total source, namely

$$\begin{aligned} \nabla _\mu \,{\tilde{T}}^{\mu \nu }=0 \ . \end{aligned}$$
(4)

In static and spherically symmetric space-times, we can parameterize the line element as

$$\begin{aligned} ds^{2} = e^{\nu }\,dt^{2}-e^{\lambda }\,dr^{2} -r^{2}\,d\varOmega ^2 \ , \end{aligned}$$
(5)

where \(\nu =\nu (r)\) and \(\lambda =\lambda (r)\) are functions of the areal radius r only and \(d\varOmega ^2=d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\). Besides,

$$\begin{aligned}&T_\mu ^{\,\,\nu }=diag[\rho ,\,-p_r,\,-p_t,\,-p_t]\ ,\end{aligned}$$
(6)
$$\begin{aligned}&\theta _\mu ^{\,\,\nu }=diag[{{\mathcal {E}}},\,-{{\mathcal {P}}}_r,\,-{{\mathcal {P}}}_t,\,-{{\mathcal {P}}}_t]\, \end{aligned}$$
(7)

from where the Einstein equations (2) read

$$\begin{aligned} \kappa \,\! \left( \rho +{{\mathcal {E}}} \right)= & {} \frac{1}{r^2} - e^{-\lambda }\left( \frac{1}{r^2}-\frac{\lambda '}{r}\right) \end{aligned}$$
(8)
$$\begin{aligned} \kappa \,\! \left( p_r+{{\mathcal {P}}}_r \right)= & {} -\frac{1}{r^2} + e^{-\lambda }\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \end{aligned}$$
(9)
$$\begin{aligned} \kappa \,\! \left( p_t+{{\mathcal {P}}}_t \right)= & {} \frac{e^{-\lambda }}{4} \left( 2\nu ''+\nu '^2-\lambda '\nu ' +2\,\frac{\nu '-\lambda '}{r}\right) \ , \end{aligned}$$
(10)

where primes indicate derivation with respect to the radial coordinate. From Eqs. (8)–(10), we identify

$$\begin{aligned} {\tilde{\rho }}= & {} T_0^{\ 0} + \theta _0^{\ 0}=\rho +{{\mathcal {E}}} \ , \end{aligned}$$
(11)
$$\begin{aligned} {\tilde{p}}_{r}= & {} -T_1^{\ 1} -\theta _1^{\ 1}=p_r+{{\mathcal {P}}}_r \ , \end{aligned}$$
(12)
$$\begin{aligned} {\tilde{p}}_{t}= & {} -T_2^{\ 2} -\theta _2^{\ 2}=p_t+{{\mathcal {P}}}_t \ , , \end{aligned}$$
(13)

as the effective energy density, and the effective radial and tangential pressure, respectively. It is worth noticing that, in general, the anisotropy

$$\begin{aligned} \varPi \equiv {\tilde{p}}_{t}-{\tilde{p}}_{r} \end{aligned}$$
(14)

does not vanish and the system of Eqs. (8)–(10) could be anisotropic.

Next, let us consider a solution to the Eqs. (2) for the seed source \(T_{\mu \nu }\) alone, namely,

(15)

which line element

$$\begin{aligned} ds^{2} = e^{\xi (r)}\,dt^{2} -e^{\mu (r)}\,dr^{2} - r^{2}\,d\varOmega ^2 \ , \end{aligned}$$
(16)

where

$$\begin{aligned} e^{-\mu (r)} \equiv 1-\frac{\kappa \,}{r}\int _0^r x^2\,T_0^{\, 0}(x)\, dx = 1-\frac{2\,m(r)}{r} \end{aligned}$$
(17)

is the well-known expression that contains the mass function \(m=m(r)\). In this regard, we can interpret the consequences of adding the source \(\theta _{\mu \nu }\) as a geometric deformation of the metric (16), namelyFootnote 3

$$\begin{aligned} \xi\rightarrow & {} \nu \,=\,\xi +g \end{aligned}$$
(18)
$$\begin{aligned} e^{-\mu }\rightarrow & {} e^{-\lambda }=e^{-\mu }+f \ , \end{aligned}$$
(19)

where f and g are respectively the geometric deformations for the radial and temporal metric components. Now, replacing (18) and (19) in (8)–(10), the Einstein equations can be separated in two sets: A) the first one given by the Einstein field equations sourced by the energy-momentum tensor \(T_{\mu \nu }\) with metric (16), namely

$$\begin{aligned} \kappa \rho= & {} \frac{1}{r^2} - e^{-\mu }\left( \frac{1}{r^{2}}-\frac{\mu '}{r}\right) , \end{aligned}$$
(20)
$$\begin{aligned} \kappa p_r= & {} -\frac{1}{r^2} + e^{-\mu }\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) , \end{aligned}$$
(21)
(22)

B) a second set containing the source \(\theta _{\mu \nu }\) which reads

$$\begin{aligned} \kappa \,{{\mathcal {E}}}= & {} -\frac{f}{r^{2}} -\frac{f'}{r}\, \end{aligned}$$
(23)
$$\begin{aligned} \kappa {{\mathcal {P}}}_r -Z_1= & {} f\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \end{aligned}$$
(24)
$$\begin{aligned} \kappa \,{{\mathcal {P}}}_t -Z_2= & {} \frac{f}{4}\left( 2\,\nu ''+\nu '^2+2\frac{\nu '}{r}\right) \frac{f'}{4}\left( \nu '+\frac{2}{r}\right) \, \end{aligned}$$
(25)

where

$$\begin{aligned} Z_1= & {} \frac{e^{-\mu }\,g'}{r} \end{aligned}$$
(26)
$$\begin{aligned} 4\,Z_2= & {} e^{-\mu }\left( 2g''+g'^2+\frac{2\,g'}{r}+2\xi '\,g'-\mu 'g'\right) . \end{aligned}$$
(27)

Note that, tensor \(\theta _{\mu \nu }\) vanishes when the deformations vanish, namely \(f=g=0\), as expected. For the particular case \(g=0\), Eqs. (23)–(25) reduce to the simpler “quasi-Einstein” system of the MGD of Ref. [30], in which f is only determined by \(\theta _{\mu \nu }\) and the undeformed metric (16). It is worth emphasizing that, in this case, the conservation equation  (4) can be written as

$$\begin{aligned}&\left[ \left( {T}_1^{\ 1}\right) ' - \frac{\xi '}{2}\left( {T}_0^{\ 0}-{T}_1^{\ 1}\right) - \frac{2}{r}\left( {T}_2^{\ 2}-{T}_1^{\ 1}\right) \right] \nonumber \\&-\frac{g'}{2}\left( {T}_0^{\ 0}-{T}_1^{\ 1}\right) +\left( {\theta }_1^{\ 1}\right) ' \nonumber \\&- \frac{\nu '}{2}\left( {\theta }_0^{\ 0}-{\theta }_1^{\ 1}\right) - \frac{2}{r}\left( {\theta }_2^{\ 2}-{\theta }_1^{\ 1}\right) = 0\ , \end{aligned}$$
(28)

where the term in brackets corresponds to the divergence of \(T_{\mu \nu }\) computed with the covariant derivative \(\nabla ^{(\xi ,\mu )}\) for the metric (16), and the last term corresponds to \(\nabla _{\sigma }\theta ^{\sigma }\ _{\nu }\) where the divergence is calculated with the deformed metric in Eq. (5). Now, as the Einstein tensor \({G}^{(\xi ,\mu )}_{\mu \nu }\) for the metric (16) satisfies its respective Bianchi identity, the momentum tensor \(T_{\mu \nu }\) is conserved in this geometry,

$$\begin{aligned} \nabla ^{(\xi ,\mu )}_\sigma \,T^{\sigma }_{\ \nu }=0 \ , \end{aligned}$$
(29)

and as a consequence (28)

$$\begin{aligned} \nabla _\sigma \theta ^{\sigma }_{\ \nu } = \frac{g'}{2}\left( \rho +p_{r}\right) \delta ^{\sigma }_{\ \nu } \ . \end{aligned}$$
(30)

At this point, a couple of comments are in order. First, note that the two sources \(T_{\mu \nu }\) and \(\theta _{\mu \nu }\) can be successfully decoupled through the GD which is particularly remarkable since it does not require any perturbative expansion in f or g [31]. Second, Eq. (30) encodes the information of energy-momentum exchange \(\varDelta \,\mathrm{E}\) between the sources, namely

$$\begin{aligned} \varDelta \,\mathrm{E}= \frac{g'}{2}\left( \rho +p_r\right) \ , \end{aligned}$$
(31)

which we can write in terms of pure geometric functions as [see Eqs. (20)–(22)]

$$\begin{aligned} \varDelta \,\mathrm{E}= \frac{g'}{2\,\kappa }\frac{e^{-\mu }}{r}\left( \xi '+\mu '\right) \ . \end{aligned}$$
(32)

From the expression (31) we can see that \(g'>0\) yields \(\varDelta \,\mathrm{E}>0\). This indicates \(\nabla _\sigma \theta ^{\sigma }_{\ \nu }>0\), according to the conservation equation (30), which means that the source \(\theta _{\mu \nu }\) is giving energy to the environment. The opposite occurs when \(g'<0\).

2.1 Matching conditions at the surface

The interior of the self-gravitating system of radius R is described by the metric (5), which we can be written as

$$\begin{aligned} ds^{2} = e^{\nu ^{-}(r)}\,dt^{2} -\left[ 1-\frac{2\,{\tilde{m}}(r)}{r}\right] ^{-1}dr^2 -r^{2}\,d\varOmega ^2 \ , \end{aligned}$$
(33)

where

$$\begin{aligned} {\tilde{m}}(r) = m(r)-\frac{r}{2}\,f(r) \ . \end{aligned}$$
(34)

In this work, we shall describe the exterior space-time by the Schwarzschild metric

$$\begin{aligned} ds^2 = \left( 1-\frac{2\,{{\mathcal {M}}}}{r}\right) \,dt^2 -\frac{dr^2}{\left( 1-\frac{2\,{{\mathcal {M}}}}{r}\right) } -r^{2}\,d\varOmega ^2\ . \end{aligned}$$
(35)

Now, to ensure the smooth continuity of the manifolds, the metrics  (33) and (35) must satisfy the Israel-Darmois matching conditions at the star surface \(\varSigma \) defined by \(r=R\). On the one hand, the continuity of the metric across \(r=R\) implies

$$\begin{aligned} e^{\nu ^{-}(R)} = 1-\frac{2\,{{\mathcal {M}}}}{R} \ , \end{aligned}$$
(36)

and

$$\begin{aligned} e^{-\lambda ^{-}(R)} = 1-\frac{2\,{{\mathcal {M}}}}{R} \ . \end{aligned}$$
(37)

On the other hand, the second fundamental form leads to

$$\begin{aligned} \left[ {\tilde{T}}_{\mu \nu }\,r^{\nu }\right] _{\varSigma } = 0 \ , \end{aligned}$$
(38)

where \(r_\mu \) is the unit radial vector normal to a surface of constant r, from where

$$\begin{aligned} p_{R} +{{\mathcal {P}}}_R = 0 \ , \end{aligned}$$
(39)

with \(p_{R}\equiv p(R)\) and \({{\mathcal {P}}}_R\equiv \,{{\mathcal {P}}}(R)\,\). Finally, the condition (39) can be written as

$$\begin{aligned} {\tilde{p}}_R\equiv \,p_{R}+\frac{f_{R}}{\kappa \,} \left( \frac{1}{R^{2}}+\frac{\nu _{R}^{\prime }}{R}\right) +\frac{g_{R}^{\prime }}{\kappa \,\,R}e^{-\mu }=0 \ , \end{aligned}$$
(40)

where \(\nu _{R}^{\prime }\equiv \partial _{r}\nu ^{-}|_{r=R}\). Eqs. (36), (37) and (40) are the necessary and sufficient conditions for matching the interior GD metric (33) with the outer Schwarzschild metric (35).

Fig. 1
figure 1

Radial pressure \([6{\tilde{p}}_r(r)\times \,10^3]\) for \(K=0.01\) and three different values of n. The pressure reach a maximum at \(r=0\) (red color) and decreases towards the surface and vanish at \(r=R\) (violet color)

Full size image
Fig. 2
figure 2

Radial pressure \([6{\tilde{p}}_r(r)\times \,10^3]\) for three different values of K and \(n=2\). Note that the pressure decreases monotonically form the center (red colored regions) towards the surface (violet colored region)

Full size image
Fig. 3
figure 3

Radial pressure \([6{\tilde{p}}_r(r,K)\times \,10^3]\) as a function of (r, K) for \(n=2\) (left panel) and \([6{\tilde{p}}_r(r,n)\times \,10^3]\) as function of (r, n) for \(K=0.01\) (right panel). The radial pressure decreases from the center (red color) towards the surface (violet color)

Full size image
Fig. 4
figure 4

Exchange of energy \([2\varDelta E\times \,10^4]\) for \(n=2\) and three different values of K. The red colored regions indicate the location where the exchange reach its maximum value. The region of maximum exchange grows as K increases

Full size image
Fig. 5
figure 5

Exchange of energy \([2\varDelta E\times \,10^4]\) for \(K=0.01\) and three different values of n. In this case the region of maximum exchange diminishes as n increases

Full size image
Fig. 6
figure 6

\([g'\times \,10^2]\) as a function of r for different values of K (left panel, \(n=2\)) and for different values of n (right panel, \(K=0.01\))

Full size image

3 Polytropic equation of state

To explore the effects of \(\theta _{\mu \nu }\) on another generic source \(T_{\mu \nu }\) described by Einstein’s equations (20)–(22) we need to provide some extra information to close the system. In this work, a first requirement is that the radial pressure satisfies the polytropic equation of state,

$$\begin{aligned} {{\mathcal {P}}}_r = K \left( {{\mathcal {E}}}\right) ^\varGamma \ne \,{{\mathcal {P}}}_t \ , \end{aligned}$$
(41)

with \(\varGamma =1+1/n\), where n is the polytropic index. The parameter \(K>0\) has dimensions of a length to the power of 2/n and contains the temperature implicitly and is governed by the thermal characteristics of a given polytrope. (For all details regarding basic concepts of polytropes, see for instance Ref. [93], also see references Refs. [12, 14, 22, 24, 25, 94]).

Let us start by using Eqs. (23) and (24) in the expression (41), which yields a first order non-linear differential equation for the deformation f,

$$\begin{aligned} \frac{{f}'}{r} + \frac{f}{r^2} =-\left( \frac{\kappa ^{\varGamma -1}}{K}\right) ^{1/\varGamma }\left[ \frac{e^{-\mu }\,g'}{r}+f\left( \frac{1}{r^2}+\frac{\nu '}{r}\right) \right] ^{1/\varGamma }\nonumber \\ \end{aligned}$$
(42)

Therefore, given a seed solution \(\{\xi ,\,\mu \}\) to Einstein equations (20)–(22), we end with a non-linear differential expression in Eq. (42) to determinate the deformations \(\{g,\,f\}\).

As a second requirement, we can impose the so-called mimic constraint for the pressure, namely, \({{\mathcal {P}}}_r\sim \,{p}_{r}\), which can be formally written as

$$\begin{aligned} {{\mathcal {P}}}_r(r)=\alpha (K,\,\varGamma ){p}_{r}(r)\ , \end{aligned}$$
(43)

where \(\alpha (K,\,\varGamma )\) is a characteristic dimensionless function for each polytrope. The simplest form for \(\alpha (K,\,\varGamma )\) consistent with the polytropic equation of state (41) and with the condition

$$\begin{aligned} f(r)\big |_{K=0}=0 \end{aligned}$$
(44)

is given by

$$\begin{aligned} \alpha (K,\,\varGamma )=\chi K^{\varGamma }, \end{aligned}$$
(45)

where \(\chi \) is a constant with dimensions of a length to the power of \(-2\varGamma /n\). Indeed, \(\chi \) could be written in terms of constants related to the seed sector. However, for future calculations, we shall assume \(\chi =1\) without loss of generality. Hence, the expression (43) becomes

$$\begin{aligned} {{\mathcal {P}}}_r(r)=K^{\varGamma }\,{p}_{r}(r)\ , \end{aligned}$$
(46)

from where  (42) and (46) read

$$\begin{aligned} \frac{{f}'}{r} + \frac{f}{r^2}= & {} -\,(\kappa \,K)^{\frac{\varGamma -1}{\varGamma }}\left[ e^{-\mu }\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) -\frac{1}{r^2}\right] ^{1/\varGamma }, \end{aligned}$$
(47)
$$\begin{aligned} g'= & {} \left( \frac{1}{e^{-\mu }+f}\right) \left[ \left( K^{\varGamma }\,e^{-\mu }-f\right) \left( \xi '+\frac{1}{r}\right) -\frac{K^{\varGamma }}{r}\right] \ .\nonumber \\ \end{aligned}$$
(48)

In summary, note that for a given seed solution \(\{\xi ,\,\mu \}\) to Einstein equations (20)–(22), we can determinate \(\{g,\,f\}\) for any polytrope \(\{K,\,\varGamma \}\) by Eqs. (47) and (48) so that this approach allows to determinate the effects of polytropes on any generic fluid satisfying Einstein equations (20)–(22), independent of its nature.

Another possibility is to consider the mimic-constrain for the density. In this case, we impose

$$\begin{aligned} {{\mathcal {E}}}(r)=\alpha (K,\varGamma )\rho =\chi K^{\varGamma }\,\rho (r)\ , \end{aligned}$$
(49)

which yields,

$$\begin{aligned} \frac{{f}'}{r} + \frac{f}{r^2}= & {} -\alpha \left[ \frac{1}{r^2} - e^{-\mu }\left( \frac{1}{r^2}-\frac{\mu '}{r}\right) \right] \ , \end{aligned}$$
(50)
$$\begin{aligned} g'= & {} \left( \frac{r}{e^{-\mu }+f}\right) \left[ \kappa \,K\left( \frac{\alpha }{\kappa }\left[ \frac{1}{r^2} - e^{-\mu }\left( \frac{1}{r^2}-\frac{\mu '}{r}\right) \right] \right) ^\varGamma \right. \nonumber \\&\left. -f\left( \frac{1}{r^2}+\frac{\xi '}{r}\right) \right] \ , \end{aligned}$$
(51)

where we have assumed \(\chi =1\) as in the previous case.

In what follows, we shall take the well-known Tolman VII models as a seed solution of Eqs. (20)–(22). Then, we shall consider a polytropic fluid, characterized by the constant K and index n in the equation of state (41). Finally, we shall consider the mimic constraint for both the pressure and density given by  (46) and (49), respectively, to ensure a polytropic fluid with acceptable physical behavior.

4 Polytropes and a perfect fluid supporting the Tolman VII geometry

In this section, we shall consider the Tolman VII solution as a seed \(\{\xi ,\mu ,\rho , p\}\) for perfect fluids [16], namely,

$$\begin{aligned} e^{\xi }= & {} B^2 \sin ^2\log \left( \sqrt{\frac{\exp \left( -\frac{\mu (r)}{2}\right) +\frac{2 r^2}{A^2}-\frac{A^2}{4 R^2}}{C}}\right) \end{aligned}$$
(52)
$$\begin{aligned} e^{-\mu }= & {} 1-\frac{r^2}{R^2}+\frac{4 r^4}{A^4} \end{aligned}$$
(53)
$$\begin{aligned} \rho _{0}= & {} \frac{1}{8 \pi }\left( \frac{3}{R^2}-\frac{20 r^2}{A^4}\right) , \end{aligned}$$
(54)
$$\begin{aligned} p_{0}= & {} \frac{ 4 A^2 R^2 \varXi (r) \cot \varPsi (r) -A^4+4 r^2 R^2}{8 \pi A^4 R^2} \end{aligned}$$
(55)
$$\begin{aligned} \varXi= & {} \sqrt{\frac{4 r^4}{A^4}-\frac{r^2}{R^2}+1}\end{aligned}$$
(56)
$$\begin{aligned} \varPsi= & {} \frac{1}{2} \log \left( \frac{\varXi (r)+\frac{2 r^2}{A^2}-\frac{A^2}{4 R^2}}{C}\right) \end{aligned}$$
(57)

where R is the radius of the stellar configuration and the constants A, B and C are determined by the matching conditions in Eqs. (36), (37) and (40) with \(f_R=g_R=0\), which leads to

$$\begin{aligned} A= & {} \left( \frac{4R^{5}}{R-2M}\right) ^{1/4}\end{aligned}$$
(58)
$$\begin{aligned} B= & {} \sqrt{\frac{5M^{2}-4MR+R^{2}}{R(R-2M)}}\end{aligned}$$
(59)
$$\begin{aligned} C= & {} \frac{(3 R-8 M) e^{-2 \cot ^{-1}\left( \frac{M}{R-2 M}\right) }}{2 \sqrt{R(R-2 M)}}, \end{aligned}$$
(60)

with the compactness \(M/R<4/9\), and \(M=m(R)\) the total mass in Eq. (17). The expressions in Eq. (58) ensure the geometric continuity at \(r=R\). It is worth mentioning that the lower value of the radius of the Tolman VII sphere is given by [28]

$$\begin{aligned} R_{Tmin}=2.589M, \end{aligned}$$
(61)

which is also the lowest radius of the extremely compact, trapping Tolman VII solution. Indeed, the upper value corresponds to \(R_{t}=3.202M\), so that, the trapping Tolman VII space-times exist for \(R_{Tmin}/M\le R/M\le R_{t}/M\). Besides, the spacetimes can be separated into two classes depending on the location of unstable null geodesics. In the first class, \(R_{Tmin}/M\le R/M\le 3\) and null geodesics are located on the exterior of the sphere. In contrast, for the second class, we have \(3\le R/M\le R_{t}/M\), and both stable and unstable null geodesics occur in the interior of the stellar configuration [28].

In what follows, we shall use Eqs. (52) and (53) we the aim to obtain the geometric deformation functions, namely \(\{f,g\}\), from either Eqs. (47) and (48) (mimic constraint for the pressure) or Eqs. (50) and (51) (mimic constraint for the density).

4.1 Mimic constraint for the pressure.

Replacing the metric functions in Eqs. (52) and (53) in the differential expression (47), we obtain the geometric deformation in terms of the polytropic index n, which reads

$$\begin{aligned} f(r) =-\frac{(8 \pi k)^{\frac{1}{n+1}} }{r}\mathcal {I}(r,n) , \end{aligned}$$
(62)

where

$$\begin{aligned} \mathcal {I}=\int \limits _{0}^{r} u^2 \left( \frac{4 u^2}{A^4}-\frac{4}{A^2} \cot \varPsi (u) \varXi (u)-\frac{1}{R^2}\right) ^{\frac{n}{n+1}}du. \end{aligned}$$
(63)

which must be numerically solved after providing the constants \(\{A,C\}\) through the matching conditions and an appropriate set of the polytropic parameters \(\{K,n\}\).

From the continuity of the first fundamental form, we obtain

$$\begin{aligned} e^{\xi (R)}e^{g_R}= & {} 1-\frac{2\,{{\mathcal {M}}}}{R} \ \end{aligned}$$
(64)
$$\begin{aligned} e^{-\mu (R)}+f_{R}= & {} 1-\frac{2\,{{\mathcal {M}}}}{R} \ , \end{aligned}$$
(65)

where \(f_{R}=f(R)\) and \(g_{R}=g(R)\) are the deformations evaluated at the surface of the star. Now, from the continuity of the second fundamental form in Eq. (40), we have

$$\begin{aligned} C=\frac{\left( A^4-16 R^4\right) }{4 A^2 R^2} e^{2 \cot ^{-1} \left( \frac{A^4}{8R^4}-\frac{1}{2}\right) }. \end{aligned}$$
(66)
Fig. 7
figure 7

Radial pressure \([6{\tilde{p}}_r(r)\times \,10^3]\) for \(K=0.01\) and three different values of n. The pressure decreases monotonously from the center (red colored region) towards the surface (violet colored region)

Full size image
Fig. 8
figure 8

Radial pressure \([6{\tilde{p}}_r(r)\times \,10^3]\) for \(n=0.2\) and three different values of K

Full size image
Fig. 9
figure 9

Radial pressure \([6{\tilde{p}}_r(r,K)\times \,10^3]\) as a function of (r, K) for \(n=0.05\) (left panel) and \([6{\tilde{p}}_r(r,n)\times \,10^3]\) as a function of (r, n) for \(K=0.01\)(right panel)

Full size image
Fig. 10
figure 10

Exchange of energy \([2\varDelta E\times \,10^4]\) for \(n=0.5\) and three different values of K. The exchange grows as K increases

Full size image
Fig. 11
figure 11

Exchange of energy \([2\varDelta E\times \,10^7]\) for \(K=0.09\) and three different values of n. Note that, he exchange of energy grows as n increases

Full size image
Fig. 12
figure 12

\([g'\times \,10^4]\) as a function of r for different values of K (left panel, \(n=0.5\)) and for different values of n (right pane, \(K=0.09\))

Full size image

It is worth emphasizing that Eqs. (64), (65) and (66) are the necessary and sufficient conditions for the matching of the interior metric (5) to a spherically symmetric outer “vacuum” described by the Schwarzschild metric in Eq. (35). Indeed, from Eqs. (47) and (48), the deformation functions f and g can be formally expressed in terms of the constants \(\{A(K,n),B(K,n),C(K,n)\}\), so that, after using (66), the problem reduces to (64) and (65) for A and B. However, as (48) and (63) must be solved numerically, the boundary values \(f_{R}\) and \(g_{R}\) remain unknown until we specify \(\{A,B,C,K,n\}\) so that the matching conditions cannot be straightforwardly implemented. To be more precise, the problem reduces to solve two equations with three unknowns, namely \(\{A,{\tilde{B}},f_{R}\}\) where we have defined \({\tilde{B}}=Be^{g_{R}}\). To solve this problem, in this work we proceed as follows. First, note that since we want to keep the Tolman VII solution when \(f=g=0\), we introduce

$$\begin{aligned} A(K,n)=A_0+\zeta (K,n)\ , \end{aligned}$$
(67)

where \(A_0\) is the perfect fluid value in Eq. (58), and \(\zeta (K,n)\) a function with dimensions of a length encoding the polytropic effects, which satisfies

$$\begin{aligned} \zeta (K,n)\big \vert _{K=0}=0\ . \end{aligned}$$
(68)

Hence, given an expression for \(\zeta (K,n)\), the problem at the stellar surface is closed. Now, as A should have dimensions of a length, we propose

$$\begin{aligned} \zeta (K,\varGamma )=K^{n/2}\ , \end{aligned}$$
(69)

where \(\zeta >0\) is in agreement with (58), which indicates that A increases as M increases [see Eq. (34) ]. Hence, for a given polytrope \(\{K,\,n\}\), we can find the effective source and the energy exchange \(\varDelta \text {E}\).

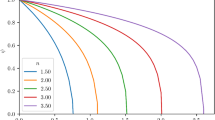
Figures 1 and 2 correspond to the effective radial pressure showing the effects of polytropes on stellar spheres explicitly. Here and in the rest of the work, we shall take \(M/R=0.2\). Note that the radial pressure decreases monotonously as expected.

In Fig. 3 (left panel) it is shown the pressure \({\tilde{p}}_r(r,K)\). Note that the maximum decreases as K grows for a fixed value of n. Similarly, in Fig. 3 (right panel) we show \({\tilde{p}}_r(r,n)\) but this time, the maximum increases with n for some K.

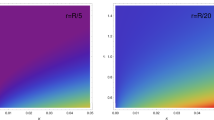
Finally, the interaction between the polytrope and the perfect fluid which produces anisotropic consequences is shown in Figs. 4 and 5. We see that, in contrast to what occurs in the Tolman IV case, the exchange of energy is minimal near both the center and the surface of the stellar configuration, and reaches a maximum at some inner core \(0<r<R\). Besides, it should be noticed that \(\varDelta E\) increases a K grows for a fixed n in contrast with what occurs in the opposite case. In both cases, as \(g'>0\) (see Fig. 6) the polytrope gives energy to the perfect fluid.

4.2 Mimic constraint for the density

In this case, the solution is analytic for f and is given by

$$\begin{aligned} f=K^{\varGamma } \left( \frac{4 r^4}{A^4}-\frac{r^2}{R^2}\right) \end{aligned}$$
(70)

Now, the matching conditions lead to

$$\begin{aligned} B^2 e^{g(R)}= & {} \frac{1-\frac{2 M}{R}}{\sin ^2\left( \log \left( \sqrt{\frac{16 R^4-A^4}{4 A^2 C R^2}}\right) \right) }\end{aligned}$$
(71)
$$\begin{aligned} A= & {} \left( \frac{4R^5 \left( K^{\varGamma }+1\right) }{ R (K^{\varGamma }+1)-2 M}\right) ^{1/4}\end{aligned}$$
(72)
$$\begin{aligned} C= & {} \frac{16 R^4-A^4}{4 A^2 R^2} \exp \left( -2 \cot ^{-1}\varPhi (r)\right) \end{aligned}$$
(73)

with

$$\begin{aligned} \varPhi= & {} \left( \frac{A^4-4 R^4-8\pi R^2 A^4 h(R,K,\varGamma )}{8 R^4}\right) \end{aligned}$$
(74)
$$\begin{aligned} h(r,K,\varGamma )= & {} \left( \frac{K^{\varGamma +\frac{1}{\varGamma } }}{\kappa ^2} \left( \frac{3}{R^2}-\frac{20 r^2}{A^4}\right) \right) ^{\varGamma }. \end{aligned}$$
(75)

The matter sector reads

$$\begin{aligned} {\tilde{\rho }}= & {} \left( K^{\frac{1}{n}+1}+1\right) \rho _{0}\end{aligned}$$
(76)
$$\begin{aligned} {\tilde{p}}_{r}= & {} h(r,K,\varGamma )+ p_{0} \end{aligned}$$
(77)

Clearly, there is also an analytical expression for the tangential pressure but, as it is too long, it will not be shown here. In Figs. 7 and 8 we show the radial pressure.

In Fig. 9 (left panel) it is shown the pressure \({\tilde{p}}_r(r,K)\). Note that the maximum decreases as K grows for a fixed value of n. Similarly, in Fig. 9 (right panel) we show \({\tilde{p}}_r(r,n)\) but this time, the maximum increases with n for some K.

Finally, the interaction between the polytrope and the perfect fluid, which produces anisotropic consequences, is shown in Figs. 10 and 11. We see that the exchange of energy is minimal near both the center and the surface of the stellar configuration, and reach a maximum at some inner core \(0<r<R\) as occurs in the previous case. Besides, it is noticeable that \(\varDelta E\) increases as both K and n grow in contrast to the previous case. In both cases, as \(g'>0\) (see Fig. 12) the polytrope gives energy to the perfect fluid.

5 Conclusions

In this work, we implemented the Gravitational Decoupling through the extended minimal geometric deformation approach to elucidate the exchange of energy between a perfect fluid and a polytrope. In particular, we use the well-known Tolman VII perfect fluid solution as a seed and use both the mimic constraint for the pressure and the density as complementary conditions to close the system of differential equations. In the first case, the geometric deformation functions, namely \(\{f,g\}\), were obtained numerically. As a consequence, the matching conditions were implemented in an alternative manner to ensure the physical acceptability of the solution. In contrast, the mimic constraint for the density leads to analytical results so that the application of Darmois’ condition was straightforward. In both cases, we explored the radial pressure and the exchange of energy between the fluids in terms of the polytropic parameters, \((K,\varGamma )\). The main result of our work is that the exchange of energy is minimum at the center, reaches a maximum at some inner core located around, and then decreases again towards the surface in contrast to what occurs when the seed is Tolman IV (as reported in [29]). Furthermore, we observed that, as occurred in [29] the flux of energy is from the polytrope to the perfect fluid. More precisely, the gradients of energy are positive (negative) for the polytrope (perfect fluid) which indicates that the polytrope needs to give up energy to achieve coexistence with the perfect fluid compatible with the exterior Schwarzschild solution.

Before concluding this work, we would like to emphasize that the study of polytropes in the framework of general relativity is not a trivial task. In particular, it is well-known that the Lane–Emden equation does not have analytic solutions. In this regard, the gravitational decoupling not only avoids the solving of the Lane–Emden equation but it allows us to explore how is the exchange of energy between the polytrope and a perfect fluid which is difficult to achieve with other approaches.

It should be interesting to explore how the exchange of energy between the polytrope and the perfect fluid affects the limits for the existence of trapping Tolman VII space-times. However, an extensive study on this and other related topics is left for future development.