Explaining muon ${g}-2$ data in the $\mu \nu$SSM

Abstract

We analyze the anomalous magnetic moment of the muon $g-2$ in the $\mu \nu$SSM. This R-parity violating model solves the $\mu$ problem reproducing simultaneously neutrino data, only with the addition of right-handed neutrinos. In the framework of the $\mu \nu$SSM, light left muon-sneutrino and wino masses can be naturally obtained driven by neutrino physics. This produces an increase of the dominant chargino-sneutrino loop contribution to muon $g-2$, solving the gap between the theoretical computation and the experimental data. To analyze the parameter space, we sample the $\mu \nu$SSM using a likelihood data-driven method, paying special attention to reproduce the current experimental data on neutrino and Higgs physics, as well as flavor observables such as B and $\mu$ decays. We then apply the constraints from LHC searches for events with multi-leptons + MET on the viable regions found. They can probe these regions through chargino–chargino, chargino–neutralino and neutralino–neutralino pair production. We conclude that significant regions of the parameter space of the $\mu \nu \mathrm{SSM}$ can explain muon $g-2$ data.

1 Introduction

One of the long standing problems of the standard model (SM) is the deviation between its prediction and the measured value of the muon anomalous magnetic dipole moment, $a_\mu = (\text {g}-2)_\mu /2$ (for a recent review, see Ref. [1]). This discrepancy has persisted even after precise measurements have been made at E821 BNL experiment [2], and theoretical calculations depending especially on the estimation of the hadronic vacuum polarization have been improved (for recent results see Refs. [3, 4]). In our analysis we used the value of $\Delta a_{\mu }= a_{\mu }^{\text {exp}}-a_{\mu }^{\text {SM}}$ from Ref. [5]¹

$$\begin{aligned} \Delta a_{\mu } = (26.8 \pm 6.3\pm 4.3) \times 10^{-10}, \end{aligned}$$

(1)

where the errors are from experiment and theory prediction (with all errors combined in quadrature), respectively. This represents a discrepancy of 3.5 times $1\,\sigma$ the combined $1\,\sigma$ error, that we will try to explain through effects of new physics beyond the SM. Besides, a new measurement of $g-2$ is underway at E989 Fermilab experiment [6] producing its first results soon, and the E34 experiment at J-PARC [7] is in preparation. They are planned to reduce the experimental uncertainty of $a_\mu$ by a factor of four, leading to a discrepancy of about $7\,\sigma$ assuming the same mean value for $a_{\mu }^{\text {exp}}$ as the BNL measurement [8, 9]. This result would be a very strong evidence of new physics.

Weak-scale supersymmetry (SUSY) has been in the forefront among handful of candidates for beyond SM theories, and has received a lot of attention from both theoretical and experimental viewpoints. If SUSY is responsible for the deviation of the measurement of $a_{\mu }$ with respect to the SM prediction, then its particle spectrum is expected to be in the vicinity of the electroweak scale, especially concerning the masses of the left muon-sneutrino, smuon and electroweak gauginos. The search for predictions of R-parity conserving (RPC) SUSY models at the experiments, such as the minimal supersymmetric standard model (MSSM) (for reviews, see e.g. Refs. [10,11,12]), puts significant bounds on sparticle masses [5], especially for strongly interacting sparticles whose masses must be above about 1 TeV. Although less stringent bounds of about 100 GeV have been obtained for weakly interacting sparticles, and the bino-like neutralino is basically not constrained at all, in models with universal soft SUSY-breaking terms at the GUT scale such as the CMSSM, NUHM1 and NUHM2 it is already not possible to fit the muon $g-2$ while respecting all the LHC constraints. Nevertheless, this is still possible in the pMSSM11 where universality is not assumed, although at the expense of either chargino or slepton coannihilation to reduce the neutralino dark matter abundance [13]. Thus some tuning in the input parameters is necessary. In addition, when the results of direct detection experiments searching for dark matter are imposed, significant constraints on the parameter space of RPC SUSY models are obtained [14,15,16,17,18,19,20,21,22,23].

On the other hand, R-parity violating (RPV) models (for reviews, see e.g. Refs. [24, 25]) are free from these tensions with dark matter and LHC constraints. Concerning dark matter, the tension is avoided since the lightest supersymmetric particle (LSP) is not stable. Concerning LHC constraints, the extrapolation of the usual bounds on sparticle masses in RPC models cannot be applied automatically to the case of RPV models. All this offers greater flexibility that can be exploited to explain more naturally the muon $g-2$ discrepancy. In this work, we will focus on the ‘$\mu$ from $\nu$’ supersymmetric standard model ($\mu \nu \mathrm{SSM}$) [25, 26], which solves the $\mu$-problem [27] of the MSSM (for a recent review, see Ref. [28]) and simultaneously reproduces neutrino data [29,30,31,32] through the presence of three generations of right-handed neutrino superfields.² In this framework, gravitino and/or axino can be candidates for dark matter with a lifetime longer than the age of the Universe, and they can be detectable with gamma-ray experiments [34,35,36,37,38,39]. Also, it was shown in Refs. [40, 41] that the LEP lower bound on masses of slepton LSPs of about 90 GeV obtained in the simplified trilinear RPV scenario [42,43,44,45,46,47], is not applicable in the $\mu \nu \mathrm{SSM}$. For the case of the bino LSP, only a small region of the parameter space of the $\mu \nu \mathrm{SSM}$ was excluded [48] when the left sneutrino is the next-to-LSP (NLSP) and hence a suitable source of binos. In particular, this happens in the region of bino (sneutrino) masses of 110–150 (110–160) GeV.

A key ingredient in SUSY to solve the discrepancy of the muon $g-2$ (for a review, see e.g. Ref. [49]), is to enhance the dominant chargino-sneutrino loop contribution by decreasing the values of the soft wino mass $M_2$ and the left muon-sneutrino mass $m_{\widetilde{\nu }_\mu }$. The $\mu \nu \mathrm{SSM}$ offers a framework where this can be obtained in a natural way. First, it is worth noting that, although RPV produces the mixing of Higgses and sneutrinos, the off diagonal terms of the mass matrix are suppressed implying that left sneutrino states are almost pure. Besides, left sneutrinos are special in the $\mu \nu \mathrm{SSM}$ because their masses are directly connected to neutrino physics, and the hierarchy in neutrino Yukawas implies also a hierarchy in sneutrino masses. This was exploited in Ref. [41] to obtain the left tau-sneutrino as the LSP, using the hierarchy $Y_{\nu _3}< Y_{\nu _1} < Y_{\nu _2}$. However, as we will show, a different hierarchy $Y_{\nu _2}< Y_{\nu _1} < Y_{\nu _3}$ is also possible to reproduce neutrino physics, giving rise to a light left muon-sneutrino. In addition, as also shown in Ref. [41], light electroweak gaugino soft masses, $M_{1,2}$, are viable reproducing correct neutrino physics. With both ingredients, light left muon-sneutrino and wino masses, the SUSY contributions to $a_\mu$ in the $\mu \nu \mathrm{SSM}$ can be sizable solving the discrepancy between theory and experiment.

In this work, we analyze first the regions of the parameter space of the $\mu \nu \mathrm{SSM}$ that feature light left muon-sneutrino and electroweak gauginos, reproducing simultaneously neutrino/Higgs physics, and flavor observables such as B and $\mu$ decays, and explaining the discrepancy shown in Eq. (1). Second, we study the constraints from LHC searches on the viable regions obtained. The latter correspond to different patterns of left muon-sneutrino and neutralino-chargino masses, which can be analysed through multi-lepton + MET searches [50, 51] from the production and subsequent decays of chargino–chargino, chargino–neutralino and neutralino–neutralino pairs.

The paper is organized as follows. In Sect. 2, we will briefly review the $\mu \nu \mathrm{SSM}$ and its relevant parameters for our analysis of the neutrino/sneutrino sector, emphasizing the special role of the sneutrino in this scenario since its couplings have to be chosen so that the neutrino oscillation data are reproduced. In Sect. 3, we will discuss the SUSY contributions to $a_{\mu }$ in the $\mu \nu \mathrm{SSM}$, studying in particular the parameters controlling them. Sect. 4 will be devoted to the strategy that we employ to perform the scan searching for points of the parameter space compatible with experimental data on neutrino and Higgs physics, as well as flavor observables, and explaining the discrepancy of the muon $g-2$. The results of the scan will be presented in Sect. 5. In Sect. 6, we will apply the constraints from LHC searches on the points found. Finally, our conclusions are left for Sect. 7.

2 The $\mu \nu \mathrm{SSM}$

2.1 Neutrino/sneutrino mass spectrum

The $\mu \nu \mathrm{SSM}$ [26] is a natural extension of the MSSM where the $\mu$ problem is solved and, simultaneously, neutrino data can be reproduced [26, 52,53,54,55,56]. This is obtained through the presence of trilinear terms in the superpotential involving right-handed neutrino superfields $\hat{\nu }^c_i$, which relate the origin of the $\mu$-term to the origin of neutrino masses and mixing angles. The simplest superpotential of the $\mu \nu \mathrm{SSM}$ [26, 52, 57] with three right-handed neutrinos is the following:

$$\begin{aligned} W= & {} \epsilon _{ab} \left( Y_{e_{ij}} \, \hat{H}_d^a\, \hat{L}^b_i \, \hat{e}_j^c + Y_{d_{ij}} \, \hat{H}_d^a\, \hat{Q}^{b}_{i} \, \hat{d}_{j}^{c} + Y_{u_{ij}} \, \hat{H}_u^b\, \hat{Q}^{a} \, \hat{u}_{j}^{c} \right) \nonumber \\&+ \epsilon _{ab} \left( Y_{{\nu }_{ij}} \, \hat{H}_u^b\, \hat{L}^a_i \, \hat{\nu }^c_j - \lambda _i \, \hat{\nu }^c_i\, \hat{H}_u^b \hat{H}_d^a \right) + \frac{1}{3} \kappa _{ijk} \hat{\nu }^c_i\hat{\nu }^c_j\hat{\nu }^c_k,\nonumber \\ \end{aligned}$$

(2)

where the summation convention is implied on repeated indices, with $a,b=1,2$ $SU(2)_L$ indices and $i,j,k=1,2,3$ the usual family indices of the SM.

The simultaneous presence of the last three terms in Eq. (2) makes it impossible to assign R-parity charges consistently to the right-handed neutrinos ($\nu _{iR}$), thus producing explicit RPV (harmless for proton decay). Note nevertheless, that in the limit $Y_{{\nu }_{ij}} \rightarrow 0$, $\hat{\nu }^c$ can be identified in the superpotential as a pure singlet superfield without lepton number, similar to the next-to-MSSM (NMSSM) [58], and therefore R parity is restored. Thus, the neutrino Yukawa couplings $Y_{\nu _{ij}}$ are the parameters which control the amount of RPV in the $\mu \nu \mathrm{SSM}$, and as a consequence this violation is small. After the electroweak symmetry breaking induced by the soft SUSY-breaking terms of the order of the TeV, and with the choice of CP conservation, the neutral Higgses ($H_{u,d}$) and right ($\widetilde{\nu }_{iR}$) and left ($\widetilde{\nu }_i$) sneutrinos develop the following vacuum expectation values (VEVs):

$$\begin{aligned} \langle H_{d}\rangle = \frac{v_{d}}{\sqrt{2}},\quad \langle H_{u}\rangle = \frac{v_{u}}{\sqrt{2}},\quad \langle \widetilde{\nu }_{iR}\rangle = \frac{v_{iR}}{\sqrt{2}},\quad \langle \widetilde{\nu }_{i}\rangle = \frac{v_{i}}{\sqrt{2}},\nonumber \\ \end{aligned}$$

(3)

where $v_{iR}\sim$ TeV, whereas $v_i\sim 10^{-4}$ GeV because of the small contributions $Y_{\nu } \lesssim 10^{-6}$ whose size is determined by the electroweak-scale seesaw of the $\mu \nu \mathrm{SSM}$ [26, 52]. Note in this sense that the last term in Eq. (2) generates dynamically Majorana masses, ${\mathcal M}_{ij}={2}\kappa _{ijk} \frac{v_{kR}}{\sqrt{2}}\sim$ TeV. On the other hand, the fifth term in the superpotential generates the $\mu$-term, $\mu =\lambda _i \frac{v_{iR}}{\sqrt{2}}\sim$ TeV.

The new couplings and sneutrino VEVs in the $\mu \nu \mathrm{SSM}$ induce new mixing of states. The associated mass matrices were studied in detail in Refs. [52, 54, 57]. Summarizing, there are eight neutral scalars and seven neutral pseudoscalars (Higgses-sneutrinos), eight charged scalars (charged Higgses-sleptons), five charged fermions (charged leptons-charginos), and ten neutral fermions (neutrinos-neutralinos). In the following, we will concentrate in briefly reviewing the neutrino and neutral Higgs sectors, which are the relevant ones for our analysis.

The neutral fermions have the flavor composition $(\nu _{i},\widetilde{B},\widetilde{W},\widetilde{H}_{d},\widetilde{H}_{u},\nu _{iR})$. Thus, with the low-energy bino and wino soft masses, $M_1$ and $M_2$, of the order of the TeV, and similar values for $\mu$ and $\mathcal {M}$ as discussed above, this generalized seesaw produces three light neutral fermions dominated by the left-handed neutrino ($\nu _i$) flavor composition. In fact, data on neutrino physics [29,30,31,32] can easily be reproduced at tree level [26, 52,53,54,55,56], even with diagonal Yukawa couplings [53, 55], i.e. $Y_{{\nu }_{ii}}=Y_{{\nu }_{i}}$ and vanishing otherwise. A simplified formula for the effective mass matrix of the light neutrinos is [55]:

$$\begin{aligned}&(m_{\nu })_{ij} \simeq \frac{Y_{{\nu }_{i}} Y_{{\nu }_{j}} v_u^2}{6\sqrt{2} \kappa v_{R}} (1-3 \delta _{ij})-\frac{v_{i} v_{j}}{4M^{\text {eff}}}\nonumber \\&\quad -\frac{1}{4M^{\text {eff}}}\left[ \frac{v_d\left( Y_{{\nu }_{i}}v_{j} +Y_{{\nu }_{j}} v_{i}\right) }{3\lambda } +\frac{Y_{{\nu }_{i}}Y_{{\nu }_{j}} v_d^2}{9\lambda ^2 }\right] , \end{aligned}$$

(4)

with

$$\begin{aligned} M^{\text {eff}}\equiv & {} M -\frac{v^2}{2\sqrt{2} \left( \kappa v_R^2+\lambda v_u v_d\right) \ 3 \lambda v_R}\nonumber \\&\times \left( 2 \kappa v_R^{2} \frac{v_u v_d}{v^2} +\frac{\lambda v^2}{2}\right) , \end{aligned}$$

(5)

and

$$\begin{aligned} \frac{1}{M} = \frac{g'^2}{M_1} + \frac{g^2}{M_2}, \end{aligned}$$

(6)

where $v^2 = v_d^2 + v_u^2 + \sum _i v^2_{i}={4 m_Z^2}/{(g^2 + g'^2)}\approx$ (246 GeV)$^2$. For simplicity, we are also assuming in these formulas, and in what follows, $\lambda _i = \lambda$, $v_{iR}= v_{R}$, and $\kappa _{iii}\equiv \kappa _{i}=\kappa$ and vanishing otherwise. We are then left with the following set of variables as independent parameters in the neutrino sector:

$$\begin{aligned} \lambda , \, \kappa ,\, Y_{\nu _i}, \tan \beta , \, v_{i}, \, v_R, \, M_1, \, M_2, \end{aligned}$$

(7)

and the $\mu$-term is given by

$$\begin{aligned} \mu =3 \lambda \frac{v_{R}}{\sqrt{2}}. \end{aligned}$$

(8)

In Eq. (7), we have defined $\tan \beta \equiv v_u/v_d$ and since $v_{i} \ll v_d, v_u$, we have $v_d\approx v/\sqrt{\tan ^2\beta +1}$. For the discussion, hereafter we will use indistinctly the subindices (1, 2, 3) $\equiv$ ($e,\mu ,\tau$). In the numerical analyses of the next sections, it will be enough for our purposes to consider the sign convention where all these parameters are positive. Of the five terms in Eq. (4), the first two are generated through the mixing of $\nu _i$ with $\nu _{iR}$-Higgsinos, and the rest of them also include the mixing with the gauginos. These are the so-called $\nu _{R}$-Higgsino seesaw and gaugino seesaw, respectively [55].

As we can understand from these equations, neutrino physics in the $\mu \nu \mathrm{SSM}$ is closely related to the parameters and VEVs of the model, since the values chosen for them must reproduce current data on neutrino masses and mixing angles.

Concerning the neutral scalars and pseudoscalars in the $\mu \nu \mathrm{SSM}$, although they have the flavor composition ($H_d, H_u, \widetilde{\nu }_{iR},\widetilde{\nu }_{i}$), the off-diagonal terms of the mass matrix mixing the left sneutrinos with Higgses and right sneutrinos are suppressed by $Y_{\nu }$ and $v_{iL}$, implying that scalar and pseudoscalar left sneutrino states will be almost pure. In addition scalars have degenerate masses with pseudoscalars $m_{\widetilde{\nu }^{\mathcal {R}}_{i}} \approx m_{\widetilde{\nu }^{\mathcal {I}}_{i}} \equiv m_{\widetilde{\nu }_{i}}$. From the minimization equations for $v_i$, we can write their approximate tree-level values as

$$\begin{aligned} m_{\widetilde{\nu }_{i}}^2 \approx \frac{Y_{{\nu }_i}v_u}{v_i} \frac{v_R}{\sqrt{2}} \left[ \frac{-T_{{\nu }_i}}{Y_{{\nu }_i}} + \frac{v_R}{\sqrt{2}} \left( -\kappa + \frac{3\lambda }{\tan \beta }\right) \right] , \end{aligned}$$

(9)

where $T_{{\nu }_i}$ are the trilinear parameters in the soft Lagrangian, $-\epsilon _{ab} T_{{\nu }_{ij}} H_u^b \widetilde{L}^a_{iL} \widetilde{\nu }_{jR}^*$, taking for simplicity $T_{{\nu }_{ii}}=T_{{\nu }_i}$ and vanishing otherwise. Therefore, left sneutrino masses introduce in addition to the parameters of Eq. (7), the

$$\begin{aligned} T_{{\nu }_i}, \end{aligned}$$

(10)

as other relevant parameters for our analysis. In the numerical analyses of Sects. 4 and 5, we will use negative values for them in order to avoid tachyonic left sneutrinos.

Let us point out that if we follow the usual assumption based on the breaking of supergravity, that all the trilinear parameters are proportional to their corresponding Yukawa couplings, defining $T_{\nu }= A_{\nu } Y_{\nu }$ we can write Eq. (9) as:

$$\begin{aligned} m_{\widetilde{\nu }_{i}}^2 \approx \frac{Y_{{\nu }_i}v_u}{v_i} \frac{v_R}{\sqrt{2}} \left[ -A_{{\nu }_i} + \frac{v_R}{\sqrt{2}} \left( -\kappa + \frac{3\lambda }{\tan \beta }\right) \right] , \end{aligned}$$

(11)

and the parameters $A_{{\nu }_i}$ substitute the $T_{{\nu }_i}$ as the most representative. We will use both type of parameters throughout this work.

Using diagonal sfermion mass matrices, from the minimization conditions for Higgses and sneutrinos one can eliminate the corresponding soft masses $m_{H_{d}}^{2}$, $m_{H_{u}}^{2}$, $m^2_{\widetilde{\nu }_{iR}}$ and $m^2_{\widetilde{L}_{iL}}$ in favor of the VEVs. Thus, the parameters in Eqs. (7) and (10), together with the rest of soft trilinear parameters, soft scalar masses, and soft gluino masses

$$\begin{aligned} T_{\lambda }, \, T_{\kappa }, \, T_{u_{i}}, \, T_{d_{i}}, \, T_{e_{i}}. \, m_{\widetilde{Q}_{iL}},\, m_{\widetilde{u}_{iR}}, \, m_{\widetilde{d}_{iR}}, \, m_{\widetilde{e}_{iR}}, \, M_3, \end{aligned}$$

(12)

constitute our whole set of free parameters. Given that we will focus on a light $\widetilde{\nu }_{\mu }$, we will use negative values for $T_{u_3}$ in order to avoid cases with too light left sneutrinos due to loop corrections.

The neutral Higgses and the three right sneutrinos, which can be substantially mixed in the $\mu \nu \mathrm{SSM}$, were discussed recently in detail in Ref. [59]. The tree-level mass of the SM-like Higgs can be written in an elucidate form for our discussion below as

$$\begin{aligned} m^{2}_{0h}= & {} {m^2_Z} \left\{ \left( \frac{1 - \mathrm{tan}^2\beta }{1 + \mathrm{tan}^2\beta }\right) ^2 + \left( \frac{v/\sqrt{2}}{m_Z}\right) ^2 \right. \nonumber \\&\times \left. ({\sqrt{3}\lambda })^2 \left( \frac{\mathrm{2\ tan\beta }}{1 + \mathrm{tan}^2\beta }\right) ^2 \right\} , \end{aligned}$$

(13)

where the factor $({v/\sqrt{2} m_Z})^2\approx 3.63$, and we have neglected for simplicity the mixing of the SM-like Higgs with the other states in the mass squared matrix. We see straightforwardly that the second term grows with small tan$\beta$ and large ${\lambda }$. If $\lambda$ is not large enough, a contribution from loops is essential to reach the target of a SM-like Higgs in the mass region around 125 GeV as in the case of the MSSM. In Refs. [33, 60, 61], a full one-loop calculation of the corrections to the neutral scalar masses was performed. Supplemented by MSSM-type corrections at the two-loop level and beyond (taken over from the code FeynHiggs [62,63,64]) it was shown that the $\mu \nu$SSM can easily accommodate a SM-like Higgs boson at $\sim 125$ GeV, while simultaneously being in agreement with collider bounds and neutrino data. This contribution is basically determined by the soft parameters $T_{u_3}, m_{\widetilde{u}_{3R}}$ and $m_{\widetilde{Q}_{3L}}$. Clearly, these parameters together with $\lambda$ and $\tan \beta$ are crucial for Higgs physics. In addition, the parameters $\kappa$, $v_R$ and $T_{\kappa }$ are the key ingredients to determine the mass scale of the right sneutrino states [52, 53]. For example, for $\lambda \lesssim 0.01$ they are basically free from any doublet contamination, and the masses can be approximated by [57, 65]:

$$\begin{aligned} m^2_{\widetilde{\nu }^{\mathcal {R}}_{iR}} \approx \frac{v_R}{\sqrt{2}} \left( T_{\kappa } + \frac{v_R}{\sqrt{2}}\ 4\kappa ^2 \right) , \quad m^2_{\widetilde{\nu }^{\mathcal {I}}_{iR}}\approx - \frac{v_R}{\sqrt{2}}\ 3T_{\kappa }. \end{aligned}$$

(14)

Given this result, we will use negative values for $T_{\kappa }$ in order to avoid tachyonic pseudoscalar right sneutrinos. Finally, the parameters $\lambda _i$ and $T_{\lambda _i}$ ($A_{\lambda _i}$ assuming the supergravity relation $T_{\lambda _i}= \lambda _i A_{\lambda _i}$) also control the mixing between the singlet and the doublet states and hence, contribute in determining the mass scale. We conclude that the relevant independent low-energy parameters in the Higgs-right sneutrino sector are the following subset of the parameters in Eqs. (7), (10), and (12):

$$\begin{aligned} \lambda ,\,\, \kappa ,\,\, \tan \beta ,\,\, v_R,\,\, T_\kappa ,\,\, T_\lambda ,\,\, T_{u_{3}},\,\, m_{\widetilde{Q}_{3L}},\,\, m_{\widetilde{u}_{3R}}. \end{aligned}$$

(15)

2.2 Neutrino/sneutrino physics

Since reproducing neutrino data is an important asset of the $\mu \nu \mathrm{SSM}$, as explained above, we will try to establish here qualitatively what regions of the parameter space are the best in order to be able to obtain correct neutrino masses and mixing angles. Although the parameters in Eq. (7), $\lambda$, $\kappa$, $v_{R}$, $\tan \beta$, $Y_{\nu _i}$, $v_{i}$, $M_1$ and $M_2$, are important for neutrino physics, the most crucial of them are $Y_{\nu _i}$, $v_{i}$ and M, where the latter is a kind of average of bino and wino soft masses (see Eq. (6)). Thus, we will first determine natural hierarchies among neutrino Yukawas, and among left sneutrino VEVs.

Considering the normal ordering for the neutrino mass spectrum, and taking advantage of the dominance of the gaugino seesaw for some of the three neutrino families, representative solutions for neutrino physics using diagonal neutrino Yukawas were obtained in Ref. [41]. In particular, the so-called type 3 solutions, which have the following structure:

$$\begin{aligned} M>0, \quad \text {with}\ Y_{\nu _2}< Y_{\nu _1}< Y_{\nu _3}, \ \text {and} \ v_1<v_2\sim v_3, \end{aligned}$$

are especially interesting for us, since, as will be argued below, they are able to produce the left muon-sneutrino as the lightest of all sneutrinos. In this case of type 3, it is easy to find solutions with the gaugino seesaw as the dominant one for the second family. Then, $v_2$ determines the corresponding neutrino mass and $Y_{\nu _2}$ can be small. On the other hand, the normal ordering for neutrinos determines that the first family dominates the lightest mass eigenstate implying that $Y_{\nu _{1}}< Y_{\nu _{3}}$ and $v_1 < v_2,v_3$, with both $\nu _{R}$-Higgsino and gaugino seesaws contributing significantly to the masses of the first and third family. Taking also into account that the composition of the second and third families in the third mass eigenstate is similar, we expect $v_3 \sim v_2$.

In addition, left sneutrinos are special in the $\mu \nu \mathrm{SSM}$ with respect to other SUSY models. This is because, as discussed in Eq. (9), their masses are determined by the minimization equations with respect to $v_i$. Thus, they depend not only on left sneutrino VEVs but also on neutrino Yukawas, and as a consequence neutrino physics is very relevant. For example, if we work with Eq. (11) assuming the simplest situation that all the $A_{{\nu }_i}$ are naturally of the order of the TeV, neutrino physics determines sneutrino masses through the prefactor ${Y_{{\nu }_i}v_u}/{v_i}$. Thus, values of ${Y_{{\nu }_i}v_u}/{v_i}$ in the range of about 0.01–1, i.e. $Y_{{\nu }_i}\sim 10^{-8}{-}10^{-6}$, will give rise to left sneutrino masses in the range of about 100-1000 GeV. This implies that with the hierarchy of neutrino Yukawas $Y_{{\nu }_{2}}\sim 10^{-8}{-}10^{-7}<Y_{{\nu }_{1,3}}\sim 10^{-6}$, we can obtain a $\widetilde{\nu }_{\mu }$ with a mass around 100 GeV whereas the masses of $\widetilde{\nu }_{e,\tau }$ are of the order of the TeV, i.e. we have $m_{\widetilde{\nu }_{2}}$ as the smallest of all the sneutrino masses. Clearly, we are in the case of solutions for neutrino physics of type 3 discussed above.

Let us finally point out that the crucial parameters for neutrino physics, $Y_{\nu _i}$, $v_{iL}$ and M, are essentially decoupled from the parameters in Eq. (15) controlling Higgs physics. Thus, for a suitable choice of $Y_{\nu _i}$, $v_{iL}$ and M reproducing neutrino physics, there is still enough freedom to reproduce in addition Higgs data by playing with $\lambda$, $\kappa$, $v_R$, $\tan \beta$, etc., as shown in Ref. [59]. As a consequence, in Sect. 5 we will not need to scan over most of the latter parameters, relaxing our demanding computing task. We will discuss this issue in more detail in Sect. 4.3.

3 SUSY contribution to $a_\mu$ in the $\mu \nu \mathrm{SSM}$

The contributions to $a_\mu$ in SUSY models, $a_{\mu }^{\text {SUSY}}$, are known to essentially come from the chargino-sneutrino and neutralino-smuon loops. In the case of the MSSM, one- and two-loop contributions have been intensively studied in the literature, as can be seen for example in Refs. [66,67,68,69] and [70,71,72,73,74,75], respectively. In the singlet(s) extension(s) of the MSSM, the contributions to $a_{\mu }^{\text {SUSY}}$ have the same expressions provided that the mixing matrices are appropriately taken into account. Nevertheless, as pointed out in Refs. [76, 77] the numerical results in these models can differ from the ones in the MSSM. Depending on the parameters of the concerned model, very light neutral scalars (few GeV) can appear at the bottom of the spectrum and the presence of such very light eigenstates can have an impact on the value of $a_{\mu }^{\text {SUSY}}$. This scenario has been also addressed in Ref. [78,79,80] in the context of two-Higgs-doublet-models. Note that although light neutralinos with leading singlino composition are possible, their contributions are small owing to their small mixing to the MSSM sector.

Fig. 1

Chargino-sneutrino (left) and neutralino-smuon (right) one-loop contributions to the anomalous magnetic moment of the muon

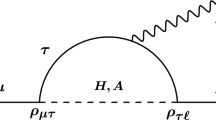
Concerning the $\mu \nu \mathrm{SSM}$, which is an extension of the MSSM with three singlet superfields, i.e. the three generations of right sneutrinos, RPV induces on the one hand, a mixing of the MSSM neutralinos and charginos with left- and right-handed neutrinos and charged leptons, respectively, and on the other hand a mixing of the Higgs doublets with the left and right sneutrinos. However, assuming that singlet scalars and pseudoscalars as well as singlino-like states are heavy, as naturally expected, their contributions are very small, and therefore the expressions of $a_{\mu }^{\text {SUSY}}$ in the $\mu \nu \mathrm{SSM}$ can be straightforwardly obtained from the MSSM. In particular, it follows that the dominant one-loop contributions to $a_{\mu }^{\text {SUSY}}$, displayed in Fig. 1, can be approximated for charginos when $\tan \beta$ is not too small, as [81]

$$\begin{aligned} a_\mu ^C\approx & {} \frac{\alpha _2 m^2_\mu }{4\pi } \frac{ \mu M_2 \tan \beta }{ m^2_{\widetilde{\nu }_\mu } } \nonumber \\&\times \left[ \frac{F_C(M_2^2/ m^2_{\widetilde{\nu }_\mu }) - F_C(\mu ^2/ m^2_{\widetilde{\nu }_\mu })}{ M_2^2 - \mu ^2 } \right] , \end{aligned}$$

(16)

and for neutralinos when there is a light bino-like neutralino, as [67, 76]

$$\begin{aligned} a_\mu ^N\approx & {} \frac{\alpha _1 m^2_\mu }{4\pi } \frac{ M_1 (\mu \tan \beta - A_\mu )}{( m^2_{\widetilde{\mu }_2} - m^2_{\widetilde{\mu }_1}) } \nonumber \\&\times \left[ \frac{F_N(M_1^2/ m^2_{\widetilde{\mu }_1})}{ m^2_{\widetilde{\mu }_1} } -\frac{ F_N(M_1^2/ m^2_{\widetilde{\mu }_2})}{ m^2_{\widetilde{\mu }_2}} \right] , \end{aligned}$$

(17)

where the loop functions are given by

$$\begin{aligned} F_C(k)= & {} \frac{3 -4k +k^2 + 2\ln k}{(1-k)^3},\nonumber \\ F_N(k)= & {} \frac{1-k^2+2k\ln k}{(1-k)^3}, \end{aligned}$$

(18)

$m_\mu$ and $m_{\widetilde{\mu }_1}$ ($m_{\widetilde{\mu }_2}$) are muon and lightest (heaviest) smuon masses, respectively, and $\alpha _i = g_i^2/(4\pi )$.

Fig. 2

$a_{\mu }^C$ versus $m_{\widetilde{\nu }_\mu }$, for different values of $M_2$ and fixed values of $\tan \beta =14$, $\mu =380$ GeV. The green and yellow bands represent the $1\sigma$ and $2\sigma$ regions of $\Delta a_\mu$ in Eq. (1), respectively, and the red dashed line the mean value

It is well known that the chargino contribution $a_\mu ^C$ is typically larger than the neutralino contribution $a_\mu ^N$ [66, 68]. Thus, in the following we concentrate our discussions on Eq. (16) in order to draw some important conclusions about the SUSY contributions to $a_\mu$, that we will check with our numerical results using the full one-loop formulas. In the light of Eq. (1), decreasing the values of $M_2$, $\mu$ or $m_{\widetilde{\nu }_\mu }$ leads to an enhancement in $a_\mu ^C$. Also, the sign of $a_\mu ^C$ is given by the sign of the product $\mu M_2$ since the factor in brackets of Eq. (16) is positive in general [68]. As discussed in Sect. 2, we are working with positive $M_2$ and $\mu$ and therefore we have a positive contribution to $a_\mu$. One the other hand, $a_\mu ^C$ increases with increasing $\tan \beta$. Thus, the parameters controlling the SUSY contributions to $a_\mu$ in the scenario that we are considering are

$$\begin{aligned} M_2, \, \mu , \, m_{\widetilde{\nu }_\mu }, \, \tan \beta , \end{aligned}$$

(19)

and they have to be appropriately chosen to satisfy in addition the constraints that we impose on Higgs/neutrino physics and flavor observables.

To qualitatively understand the behaviour of the dominant contribution to $a_{\mu }^{\text {SUSY}}$, as an example we show $a_\mu ^C$ versus $m_{\widetilde{\nu }_\mu }$ in Fig. 2 for several values of the other relevant parameters. As we can see, for the cases studied with $\tan \beta = 14$ and $\mu =380$ GeV, $a_\mu ^C$ is compatible at to $2 \sigma$ with $\Delta a_\mu$ in Eq. (1) for $m_{\widetilde{\nu }_\mu } \lesssim 600$ (100) GeV corresponding to $M_2 = 150$ (900) GeV. For larger sneutrino masses the contribution to $a_\mu ^C$ is too small. On the contrary, this contribution turns out to be too large for small masses $m_{\widetilde{\nu }_\mu } \lesssim 200$ GeV in the case of $M_2 =150$ GeV. We will check these features with the numerical results presented in Sect. 5.

4 Strategy for the scanning

In this section, we describe the methodology that we have employed to search for points of our parameter space that are compatible with the current experimental data on neutrino and Higgs physics as well as with the measurement of $\Delta a_\mu$. In addition, we have demanded the compatibility with some flavor observables, such as B and $\mu$ decays. To this end, we have performed a scan on the parameter space of the model, with the input parameters optimally chosen as will be discussed in Sect. 4.3.

4.1 Sampling the $\mu \nu \mathrm{SSM}$

For the sampling of the $\mu \nu \mathrm{SSM}$, we have used a likelihood data-driven method employing the Multinest [82] algorithm as optimizer. The goal is to find regions of the parameter space of the $\mu \nu \mathrm{SSM}$ that are compatible with the given experimental data. It is worth noting here that we are not performing any statistical interpretation of the set of points obtained, i.e. the Multinest algorithm is just used to obtain viable points.

For this purpose we have constructed the joint likelihood function:

$$\begin{aligned} {\mathcal {L}}_{\text {tot}}= & {} {\mathcal {L}}_{a_\mu } \times {\mathcal {L}}_{\text {neutrino}} \times {\mathcal {L}}_{\text {Higgs}} \times {\mathcal {L}}_{\text {B physics}} \times {\mathcal {L}}_{\mu \text {decay}} \nonumber \\&\times {\mathcal {L}}_{m_{\widetilde{\chi }^\pm }}, \end{aligned}$$

(20)

where ${\mathcal {L}}_{a_\mu }$ is the constraint from the muon anomalous magnetic moment, ${\mathcal {L}}_{\text {neutrino}}$ represents measurements of neutrino observables, ${\mathcal {L}}_{\text {Higgs}}$ Higgs observables, ${\mathcal {L}}_{\text {B physics}}$ B-physics constraints, ${\mathcal {L}}_{\mu \text { decay}}$ $\mu$ decay constraints and ${\mathcal {L}}_{m_{\widetilde{\chi }^\pm }}$ LEPII constraints on the chargino mass.

To compute the spectrum and the observables we have used SARAH [83] to generate a SPheno [84, 85] version for the model. We condition that each point is required not to have tachyonic eigenstates. For the points that pass this constraint, we compute the likelihood associated to each experimental data set and for each sample all the likelihoods are collected in the joint likelihood ${\mathcal {L}}_{\text {tot}}$ above.

4.2 Likelihoods

We used three types of likelihood functions in our analysis. For observables in which a measure is available we use a Gaussian likelihood function defined as follows

$$\begin{aligned} {\mathcal {L}}(x) = \exp \left[ -\frac{(x-x_0)^2}{2(\sigma _{\text {exp}}^2 +\tau ^2)} \right] , \end{aligned}$$

(21)

where $x_0$ is the experimental best fit set on the parameter x, and $\sigma _{\text {exp}}$ and $\tau$ are the experimental and theoretical uncertainties on the observable x, respectively. Since in our scan we are not performing a statistical analysis, we take the value of $\tau$ in such a way that a set of points is obtained with their values close enough to the mean value of the corresponding observable. This is used to impose subsequently to these points the criteria of acceptance that will be discussed below in Sect. 5.

On the other hand, for any observable for which the constraint is set as a lower limit, such as the chargino mass lower bound, the likelihood function is defined as [86]

$$\begin{aligned} {\mathcal {L}}(x)= & {} \frac{\sigma _{\text {exp}}}{\sqrt{\sigma _{\text {exp}}^2+\tau ^2}} \left[ 1-K\left( D(x)\right) \right] \nonumber \\&\times \exp \left[ -\frac{(x-x_0)^2}{2(\sigma _{\text {exp}}^2+\tau ^2)}\right] + K\left( \frac{x-x_0}{\tau }\right) , \end{aligned}$$

(22)

where

$$\begin{aligned} D(x) = \frac{\sigma _{\text {exp}}}{\tau } \left( \frac{x_0 - x}{\sqrt{\sigma _{\text {exp}}^2 +\tau ^2}} \right) ,\quad K(a) = \frac{1}{2} \text {erfc}\left( \frac{a}{\sqrt{2}}\right) , \nonumber \\ \end{aligned}$$

(23)

with erfc is the complementary error function.

Table 1 Neutrino data used in the sampling of the $\mu \nu \mathrm{SSM}$ for the anomalous magnetic moment of the muon

The last class of likelihood function we used is a step function in such a way that the likelihood is one/zero if the constraint is satisfied/non-satisfied.

Subsequently, we present each constraint used in this work together with the corresponding type of likelihood function.

Muon anomalous magnetic moment

The main goal of this work is to explain the current $3.5 \,\sigma$ discrepancy between the measurement of the anomalous magnetic moment of the muon and the SM prediction $\Delta a_\mu$ in Eq. (1), therefore we impose $a_{\mu }^{\text {SUSY}}=\Delta a_\mu$. The corresponding likelihood is ${\mathcal {L}}_{a_\mu }$, and we used $\tau =2\times 10^{-10}$.

Neutrino observables

We used the results for normal ordering from Ref. [32] summarized in Table 1, where $\Delta m^2_{ij}=m_i^2-m_j^2$. For each of the observables listed in the neutrino sector, the likelihood function is a Gaussian (see Eq. (21)) centered at the mean value $x_0$ and with width $\sigma _{\text {exp}}$. Concerning the cosmological upper bound on the sum of the masses of the light active neutrinos given by $\sum m_{\nu _i} < 0.12$ eV [87], even though we did not include it directly in the total likelihood, we imposed it on the viable points obtained.

Higgs observables

Before the discovery of the SM-like Higgs boson, the negative searches of Higgs signals at the Tevatron, LEP and LHC, were transformed into exclusions limits that must be used to constrain any model. Its discovery at the LHC added crucial constraints that must be taken into account in those exclusion limits. We have considered all these constraints in the analysis of the $\mu \nu \mathrm{SSM}$, where the Higgs sector is extended with respect to the MSSM as discussed in Sect. 2. For constraining the predictions in that sector of the model, we interfaced HiggsBounds v5.3.2 [88, 89] with MultiNest. First, several theoretical predictions in the Higgs sector (using a conservative $\pm 3$ GeV theoretical uncertainty on the SM-like Higgs boson) are provided to determine which process has the highest exclusion power, according to the list of expected limits from Tevatron, LEP and LHC. Once the process with the highest statistical sensitivity is identified, the predicted production cross section of scalars and pseudoscalars multiplied by the branching ratios (BRs) are compared with the limits set by these experiments. Then, whether the corresponding point of the parameter under consideration is allowed or not at 95% confidence level is indicated. In constructing the likelihood from HiggsBounds constraints, the likelihood function is taken to be a step function. Namely, it is set to one for points for which Higgs physics is realized, and zero otherwise. Finally, in order to address whether a given Higgs scalar of the $\mu \nu \mathrm{SSM}$ is in agreement with the signal observed by ATLAS and CMS, we interfaced HiggsSignals v2.2.3 [90, 91] with MultiNest. A $\chi ^2$ measure is used to quantitatively determine the compatibility of the $\mu \nu \mathrm{SSM}$ prediction with the measured signal strength and mass. The experimental data used are those of the LHC with some complements from Tevatron. The details of the likelihood evaluation can be found in Refs. [90, 91].

B decays

$b \rightarrow s \gamma$ is a flavour changing neutral current (FCNC) process, and hence it is forbidden at tree level in the SM. However, it occurs at leading order through loop diagrams. Thus, the effects of new physics (in the loops) on the rate of this process can be constrained by precision measurements. In the combined likelihood, we used the average value of $(3.55 \pm 0.24) \times 10^{-4}$ provided in Ref. [92]. Notice that the likelihood function is also a Gaussian (see Eq. (21)). Similarly to the previous process, $B_s \rightarrow \mu ^+\mu ^-$ and $B_d \rightarrow \mu ^+\mu ^-$ are also forbidden at tree level in the SM but occur radiatively. In the likelihood for these observables (21), we used the combined results of LHCb and CMS [93], $\text {BR} (B_s \rightarrow \mu ^+ \mu ^-) = (2.9 \pm 0.7) \times 10^{-9}$ and $\text {BR} (B_d \rightarrow \mu ^+ \mu ^-) = (3.6 \pm 1.6) \times 10^{-10}$. Concerning the theoretical uncertainties for each of these observables we take $\tau = 10 \%$ of the corresponding best fit value. We denote by ${\mathcal {L}}_{\text {B physics}}$ the likelihood from $b \rightarrow s \gamma$, $B_s \rightarrow \mu ^+\mu ^-$ and $B_d \rightarrow \mu ^+\mu ^-$.

$\mu \rightarrow e \gamma$ and $\mu \rightarrow e e e$

We also included in the joint likelihood the constraint from BR$(\mu \rightarrow e\gamma ) < 5.7\times 10^{-13}$ and BR$(\mu \rightarrow eee) < 1.0 \times 10^{-12}$. For each of these observables we defined the likelihood as a step function. As explained before, if a point is in agreement with the data, the likelihood ${\mathcal {L}}_{\mu \text {decay}}$ is set to 1 otherwise to 0.

Chargino mass bound

In RPC SUSY, the lower bound on the lightest chargino mass of about 94 GeV depends on the spectrum of the model [5, 94]. Although in the $\mu \nu \mathrm{SSM}$ there is RPV and therefore this constraint does not apply automatically, to compute ${\mathcal {L}}_{m_{\widetilde{\chi }^\pm }}$ we have chosen a conservative limit of $m_{\widetilde{\chi }^\pm _1} > 92$ GeV with $\tau = 5 \%$ of the chargino mass.

4.3 Input parameters

In order to efficiently scan for $a_{\mu }^{\text {SUSY}}$ in the $\mu \nu \mathrm{SSM}$ to reproduce $\Delta a_\mu$, it is important to identify the parameters to be used, and optimize their number and their ranges of values. As discussed in Sect. 2.2, the most relevant parameters in the neutrino sector of the $\mu \nu \mathrm{SSM}$ are $v_i, Y_{\nu _i}$ and M. Concerning M, we will assume $M_2=2M_1$ and scan over $M_2$. This relation is inspired by GUTs, where the low-energy result $M_2= (\alpha _2/\alpha _1) M_1\simeq 2 M_1$ is obtained, with $g_2=g$ and $g_1=\sqrt{5/3}\ g'$. On the other hand, sneutrino masses introduce in addition the parameters $T_{{\nu }_i}$ (see Eq. (9)). In particular, $T_{{\nu }_2}$ is the most relevant one for our discussion of a light $\widetilde{\nu }_{\mu }$, and we will scan it in an appropriate range of small values. Since the left sneutrinos of the other two generations can be heavier, we will fix $T_{{\nu }_{1,3}}$ to a larger value. The parameter $\tan \beta$ is important for Higgs physics, thus we will consider a narrow range of possible values to ensure good Higgs physics.

Summarizing, we will perform scans over the 9 parameters $Y_{\nu _i}, v_i, T_{{\nu }_2}, \tan \beta , M_2$, as shown in Table 2, using log priors (in logarithmic scale) for all of them, except for $\tan \beta$ which is taken to be a flat prior (in linear scale). The ranges of $v_i$ and $Y_{\nu _i}$ are natural in the context of the electroweak-scale seesaw of the $\mu \nu \mathrm{SSM}$, as discussed in Sect. 2. The range of $T_{\nu _{2}}$ is chosen to have light $\widetilde{\nu }_{\mu }$ below about 600 GeV. This is a reasonable upper bound to be able to have sizable SUSY contributions to $a_\mu$. If we follow the usual assumption based on the supergravity framework discussed in Eq. (11) that the trilinear parameters are proportional to the corresponding Yukawa couplings, i.e. in this case $T_{\nu _{2}}= A_{\nu _{2}} Y_{\nu _2}$, then $-A_{\nu _{2}}\in$ ($1, 4\times 10^{4}$) GeV.

Table 2 Range of low-energy values of the input parameters that are varied in the scan, where $Y_{\nu _{i}}$, $v_i$, $T_{\nu _{2}}$ and $M_2$ are $\log$ priors while $\tan \beta$ is a flat prior. The VEVs $v_i$, and the soft parameters $T_{\nu _{2}}$ and $M_2$, are given in GeV. The GUT-inspired low-energy relation $M_2=2M_1$ is assumed

Table 3 Low-energy values of the input parameters that are fixed in the scan. The VEV $v_R$ and the soft trilinear parameters, soft gluino masses and soft scalar masses are given in GeV

Other benchmark parameters relevant for Higgs physics are fixed to appropriate values, and are shown in Table 3. As one can see, we choose a small/moderate value for $\lambda \approx 0.1$. Thus, we are in a similar situation as in the MSSM, and moderate/large values of $\tan \beta$, $|T_{u_{3}}|$, and soft stop masses, are necessary to obtain through loop effects the correct SM-like Higgs mass, as discussed in Eq. (13). In addition, if we want to avoid the chargino mass bound of RPC SUSY, the value of $\lambda$ also forces us to choose a moderate/large value of $v_R$ to obtain a large enough value of $\mu =3 \lambda \frac{v_{R}}{\sqrt{2}}$. In particular, we choose $v_R=1750$ GeV giving rise to $\mu \approx 379$ GeV. As explained in Eq. (14), the parameters $\kappa$ and $T_{\kappa }$ are also crucial to determine the mass scale of the right sneutrinos. Since we choose $T_{\kappa }=-390$ GeV to have heavy pseudoscalar right sneutrinos (of about 1190 GeV), the value of $\kappa$ has to be large enough in order to avoid too light (even tachyonic) scalar right sneutrinos. Choosing $\kappa =0.4$, we get masses for the latter of about 700–755 GeV. The parameter $T_{\lambda }$ is relevant to obtain the correct values of the off-diagonal terms of the mass matrix mixing the right sneutrinos with Higgses, and we choose for its value 340 GeV.

The values of the other parameters, shown below $m_{\widetilde{u}_{3R}}$ in Table 3, concern gluino, squark and slepton masses, and quark and lepton trilinear parameters, and are not specially relevant for our scenario of muon $g-2$. Finally, compared to the values of $T_{\nu _{2}}$, the values chosen for $T_{\nu _{1,3}}$ are natural within our framework $T_{\nu _{1,3}}= A_{\nu _{1,3}} Y_{\nu _{1,3}}$, since larger values of the Yukawa couplings are required for similar values of $A_{\nu _{i}}$. In the same way, the values of $T_{d_3}$ and $T_{e_3}$ have been chosen taking into account the corresponding Yukawa couplings.

Fig. 3

$-A_{\nu _2}$ versus $Y_{\nu _2} v_u/{v_2}$. The colours indicate different values of the left muon-sneutrino mass

Fig. 4

$v_2$ versus $Y_{\nu _2}$ for the scan. The colours indicate different values of the gaugino mass parameter M defined in Eq. (6)

5 Results of the scan

Following the methods described in the previous sections, to find regions consistent with experimental observations we have performed about 36 million of spectrum evaluations in total and the total amount of computer required for this was approximately 190 CPU years.

To carry this analysis out, we select points from the scan that lie within $\pm 3\sigma$ of all neutrino physics observables [32] summarized in Table 1. Second, we put $\pm 3\sigma$ cuts from $b \rightarrow s \gamma$, $B_s \rightarrow \mu ^+\mu ^-$ and $B_d \rightarrow \mu ^+\mu ^-$ and require the points to satisfy also the upper limits of $\mu \rightarrow e \gamma$ and $\mu \rightarrow eee$. In the third step, we impose that Higgs physics is realized. In particular, we require that the p-value reported by HiggsSignals be larger than 5%. We also check with Vevacious [95] that the electroweak symmetry-breaking vacua corresponding to the previous allowed points are stable. The points found will be discussed in Sect. 5.1. Finally, since we want to explain the current experimental versus theoretical discrepancy in the muon anomalous magnetic moment, of the allowed points we select those within $\pm 2 \sigma$ of $\Delta a_\mu$. The resulting points will be presented in Sect. 5.2.

5.1 Constraints from neutrino and light $\tilde{\nu }_{\mu }$ physics

Imposing all the cuts discussed above, we show in Fig. 3 the values of the parameter $A_{\nu _2}$ versus the prefactor in Eq. (11), $Y_{\nu _2} v_u/{v_2}$, giving rise to different values for the mass of the $\widetilde{\nu }_{\mu }$. The colours indicate different values of this mass. Let us remark that the plot has been obtained using the full numerical computation including loop corrections, although the tree-level mass in Eq. (11) gives a good qualitative idea of the results. We found solutions with $A_{\nu _2}$ in the range $-A_{\nu _2}\in$ ($861, 25.5\times 10^4$) GeV, corresponding to $-T_{\nu _2}\in$ ($8.8\times 10^{-6}, 3.8\times 10^{-4}$) GeV, but for the sake of naturalness we prefer to discuss only those solutions with the upper bound for $-A_{\nu _2}$ in 5 TeV. These are the ones shown in Fig. 3. In any case, larger values of $-A_{\nu _2}$ increase the sneutrino mass, being disfavoured by the value of the muon $g-2$. Thus, our solutions correspond to $-A_{\nu _2}\in$ ($861, 5\times 10^3$) GeV with $-T_{\nu _2}\in$ ($10^{-5}, 3\times 10^{-4}$) GeV. We can see, as can be deduced from Eq. (11), that for a fixed value of $-A_{\nu _2}$ ($Y_{\nu _2} v_u/{v_2}$) the greater $Y_{\nu _2} v_u/{v_2}$ ($-A_{\nu _2}$) is, the greater $m_{\widetilde{\nu }_{\mu }}$ becomes. Let us finally note that $m_{\widetilde{\nu }_{\mu }}$ is always larger than 64 GeV, which corresponds to about half of the mass of the SM-like Higgs (remember that we allow a ±3 GeV theoretical uncertainty on its mass). For smaller masses, the latter would dominantly decay into sneutrino pairs, leading to an inconsistency with Higgs data [41].

Fig. 5

$\Delta m^2_{21}$ versus neutrino Yukawas (left) and left sneutrino VEVs (right). Colors blue, green and grey correspond to $i=1,2,3$, respectively

In Fig. 4, we show $v_2$ versus $Y_{\nu _2}$, with the colours indicating now different values of M. There we can see that the greater $v_2$ is, the greater M becomes. In addition, for a fixed value of $v_2$, M is quite independent of the variation in $Y_{\nu _2}$. This confirms that, as explained in Sect. 2.2, the gaugino seesaw is the dominant one for the second neutrino family. From the figure, we can see that the range of M reproducing the correct neutrino physics is 223–1467 GeV corresponding to $M_2$ in the range 152–1000 GeV.

The values of $Y_{\nu _{2}}$ and $v_2$, used in order to obtain a light $\widetilde{\nu }_{\mu }$, in turn constrain the values of $Y_{\nu _{1,3}}$ and $v_{1,3}$ producing a correct neutrino physics. This is shown in Fig. 5, where $\Delta m^2_{21}$ versus $Y_{\nu _{i}}$ and $v_i$ is plotted. As we can see, we obtain the hierarchy qualitatively discussed in Sect. 2.2, i.e. $Y_{\nu _{2}}< Y_{\nu _{1}} < Y_{\nu _{3}}$, and $v_1 < v_3\lesssim v_2$. Concerning the absolute value of neutrino masses, we obtain $m_{\nu _1}\sim$ 0.001–0.002 eV, $m_{\nu _2}\sim$ 0.008–0.009 eV, and $m_{\nu _3}\sim$ 0.05 eV, fulfilling the cosmological upper bound on the sum of neutrino masses of 0.12 eV mentioned in Sect. 4.2. The predicted value of the sum of the neutrino masses can be tested in future CMB experiments such as CMB-S4 [96].

Fig. 6

$a_\mu ^{\text {SUSY}}$ versus $\tan \beta$ from the scan of Tables 2 and 3. The green and blue colors represent points in the $1\sigma$ and $2\sigma$ regions of $\Delta a_\mu$ in Eq. (1), respectively. The red points are not within the $2\sigma$ cut on $\Delta a_\mu$

Fig. 7

$a_\mu ^{\text {SUSY}}$ versus $M_2$ from the scan of Tables 2 and 3. The color code is the same as in Fig. 6

Fig. 8

$a_\mu ^{\text {SUSY}}$ versus $m_{\widetilde{\nu }_\mu }$ from the scan of Tables 2 and 3. The color code is the same as in Fig. 6

5.2 Constraints from muon $g-2$

Once neutrino (and sneutrino) physics has determined the relevant regions of the parameter space of the $\mu \nu \mathrm{SSM}$ with light left muon-sneutrino mass consistent with Higgs physics, we are ready to analyze the subset of regions that can explain the deviation between the SM prediction and the experimental value of the muon anomalous magnetic moment.

As discussed in Sect. 4.3, we have chosen $\mu \approx 379$ GeV, thus, from Eq. (19) the relevant parameters to determine the chargino-sneutrino contribution to $a_\mu ^{\text {SUSY}}$ are $M_2$, $m_{\widetilde{\nu }_\mu }$ and $\tan \beta$. In the following we will discuss the $\Delta a_\mu$ constraint on these parameters.

First, we expect $\tan \beta$ not to have notable effects on the $a_\mu ^{\text {SUSY}}$ considering the narrow range, between 10–16, that we have chosen for it. This is shown in Fig. 6, where all the points found in the previous subsection are plotted. As we can see, although not all of them (red points) are within the $2\sigma$ cut on $\Delta a_\mu$, there are many not only in the $2\sigma$ (blue) but also in the $1\sigma$ region (green). Obviously, the green points are also included in the $2\sigma$ region of the blue points. As expected, $a_\mu ^{\text {SUSY}}$ is quite independent of the variation of $\tan \beta$ in the range 10–16.

On the other hand, the effects are expected to be significant with the variations of $M_2$ and $m_{\widetilde{\nu }_\mu }$, for the ranges analyzed in our scan. In Figs. 7 and 8, we show $a_\mu ^{\text {SUSY}}$ versus $M_2$ and $m_{\widetilde{\nu }_\mu }$, respectively. As we can see, now the smaller $M_2$ ($m_{\widetilde{\nu }_\mu }$) is, the greater $a_\mu ^{\text {SUSY}}$ becomes. For example, for $M_2$ from $\sim 800$ to 200 GeV, the SUSY contribution to $a_\mu$ increases from about 13 to 40 in units of $10^{-10}$. The same increase in $a_\mu ^{\text {SUSY}}$ occurs when $m_{\widetilde{\nu }_\mu }$ decreases from $\sim 440$ to 100 GeV, Also, one can explain the $1\,\sigma$ ($2\,\sigma$) region of $\Delta a_\mu$ with values of $M_2$ smaller than about 510 (920) GeV, and with values of $m_{\widetilde{\nu }_\mu }$ smaller than 302 (422) GeV. In sum, this result agrees with the features of Fig. 2, and confirms as expected that in our scenario Eq. (16) can be qualitatively used to describe the SUSY contribution to $a_\mu$.

Fig. 9

$m_{\widetilde{\nu }_\mu }$ versus $M_2$ from the scan of Tables 2 and 3. The color code is the same as in Fig. 6. The viable points (green and blue) are classified in three categories: The dot symbol corresponds to points with left muon-sneutrino mass smaller than bino mass, the cross corresponds to sneutrino mass between bino and wino masses, and the triangle is for points with sneutrino mass heavier than wino mass. We assume in our scan the GUT-inspired low-energy relation $M_1=M_2/2$, and therefore $m_{\widetilde{B}^0}<m_{\widetilde{W}}$

Figure 9 can be regarded as the summary of our results. There we show $m_{\widetilde{\nu }_\mu }$ versus $M_2$. We find (green) points in the $1\sigma$ region of $\Delta a_\mu$ in the mass ranges $72 \lesssim m_{\widetilde{\nu }_\mu }\lesssim 302$ GeV and $152 \lesssim M_2\lesssim 510$ GeV. The (blue) points in the $2\sigma$ region are in the wider ranges $64 \lesssim m_{\widetilde{\nu }_\mu }\lesssim 422$ GeV and $152 \lesssim M_2\lesssim 920$ GeV. Concerning the physical gaugino masses, these ranges of $M_2$ correspond to bino masses in the range about 73–465 GeV and wino masses between 152–945 GeV. We conclude that significant regions of the parameter space of the $\mu \nu \mathrm{SSM}$ can solve the discrepancy between theory and experiment in the muon $g-2$, reproducing simultaneously neutrino and Higgs physics, as well as flavour observables.

Let us finally mention that the viable points (green and blue) are classified in Fig. 9 in three different categories as explained in the caption. This categorization will be important in the next section where the constraints from LHC searches are taken into account. For example, the presence of light left muon-sneutrinos and winos, or light long-lived binos, could be excluded by LHC searches of particles decaying into lepton pairs.

6 Constraints from LHC searches

Depending on the different masses and orderings of the lightest SUSY particles of the spectrum found in our scan, we expect different signals at colliders. As shown in Fig. 9, the possible situations can be classified in three cases: (i) the left muon-sneutrino is the LSP, (ii) the bino-like neutralino is the LSP and the left muon-sneutrino is the NLSP, and (iii) the bino-like neutralino is the LSP and the wino-like neutralino-chargino are co-NLSPs. In addition, depending on the value of the parameters, the decay of the LSP can be prompt or displaced. Altogether, there is a variety of possible signals arising from the regions of the parameter space analyzed in the previous sections, that could be constrained using LHC searches. In the following, we will use indistinctly the notation $\widetilde{\chi }^0$, $\widetilde{\chi }^\pm$, or $\widetilde{B}^0$, $\widetilde{W}^0$, $\widetilde{W}^\pm$, $\widetilde{H}^\pm$, etc.

6.1 Case (i) $m_{\tilde{\nu }_\mu }<m_{\tilde{B}^0} < m_{\tilde{W}^0}$

Let us consider first the case with a left muon-sneutrino as the LSP. As analyzed in Refs. [40, 41, 57], the main decay channel of the LSP corresponds to neutrinos, which constitute an invisible signal. Limits on sneutrino LSP from mono-jet and mono-photon searches have been discussed in the context of the $\mu \nu \mathrm{SSM}$ in Refs. [40, 41], and they turn out to be ineffective to constrain it. However, the presence of charginos and neutralinos in the spectrum with masses not far above from that of the LSP is relevant to multi-lepton+MET searches. In particular, the production of wino/higgsino-like chargino pair at the LHC can produce the signal of $2\mu +4\nu$, as shown in Fig. 10. These processes produce a signal similar to the one expected from a directly produced pair of smuons decaying as $\widetilde{\mu }\rightarrow \mu +\widetilde{\chi }^0$ in RPC models. Therefore, they can be compared with the limits obtained by the ATLAS collaboration in the search for sleptons in events with two leptons $+$ MET [50].

To carry this analysis out, we will compare the limits on the signal cross section available in the auxiliary material of Ref. [50] with the production cross section of the chargino pair times BR$(\widetilde{\chi }^{\pm }\rightarrow \mu \ \widetilde{\nu }_\mu )\times$ BR$( \widetilde{\nu }_\mu \rightarrow \nu \nu )$, where the former is calculated using RESUMMINO-2.0.1 [97,98,99,100] at NLO.

Fig. 10

Production of chargino pair decaying to left muon-sneutrino, which in turn decays to neutrinos, giving rise to the signal $2\mu +\mathrm {MET}$

Let us finally point out that other decay modes are possible for the wino-like charginos, in particular chains involving higgsinos when $M_2>\mu$. However, the search is designed to require exactly two opposite-sign leptons plus MET and the presence of additional leptons, b-jets, or multiple non b-jets, will make the candidate events to be discarded. An exception is the decay of wino-like charginos to lighter higgsino-like charginos plus Z bosons. The produced signal will be similar to the one shown in Fig. 10, with the addition of two Z bosons that would not spoil the signal as long as they decay to neutrinos. This process will have therefore a similar effective cross section as the one in Fig. 10, but the additional suppression from the branching fraction of both Z bosons to neutrinos makes the channel subdominant.

We have also considered the signals produced in events where two neutral higgsinos are directly produced and decay into two smuons plus two muons, giving rise to a final signal with $4\mu +$ MET. This signal could be compared with the ATLAS search for SUSY in events with four or more leptons [101]. However, the signal regions are optimised to look for SUSY particles with masses above 600 GeV. In our scan we have fixed $\mu \approx 379$ GeV following the discussion of Sect. 4.3, thus the events initiated by higgsinos with a mass of that order are ineffective passing the selection cuts. Although we will also explore in Sect. 6.4 regions of the parameter space with higgsino masses of about 800 GeV, satisfying therefore the kinematical requirements, their production cross section turns out to be too small. In this scenario, we have also considered the search for events with 2 leptons $+$ MET [50] or 3 leptons $+$ MET [102] in the case where two or one of the muons would remain undetected. However, higgsinos have enough energy to make all the muons produced in the decay chain detectable.

6.2 Case (ii) $m_{\tilde{B}^0}<m_{\tilde{\nu }_\mu }< m_{\tilde{W}^0}$

The bino-like neutralino can also be the LSP, with the left muon-sneutrino lighter than the wino-higgsino-like chargino–neutralino. Then, the production of a chargino–neutralino will produce sneutrinos-smuons in the decay. When the mass of the bino is $m_{\widetilde{B}^0} \lesssim m_W$ its decay is suppressed in comparison with the one of the left sneutrino LSP. This is because of the kinematical suppression associated with the three-body nature of the bino decay. For this reason, it is natural that the bino proper decay length is an order of magnitude larger than the one of the left sneutrino, being therefore of the order of ten centimeters. The points of the parameter space where the LSP decays with a proper decay distance larger than 1 mm can be constrained applying the limits on long-lived particles (LLPs) obtained by the ATLAS 8 TeV search [51], as explained in the following.

The proton–proton collisions produce a pair chargino–chargino, chargino–neutralino or neutralino–neutralino of dominant wino composition as shown in Fig. 11. The charginos and neutralinos will rapidly decay to sneutrinos/smuons and muons/neutrinos, with the former subsequently decay to muons/neutrinos plus long-lived binos. The possible decays form the following combinations:

• (1) $p p \rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{\pm }_j\rightarrow 3\mu \ \nu \ 2[\widetilde{\chi }^0_1]_{displaced}$

• (2) $p p \rightarrow \widetilde{\chi }^{\pm }_i\ \widetilde{\chi }^{{\mp }}_j\rightarrow 2\mu \ 2\nu \ 2[\widetilde{\chi }^0_1]_{displaced}$

• (3) $p p \rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{\pm }_j\rightarrow \mu \ 3\nu \ 2[\widetilde{\chi }^0_1]_{displaced}$

• (4) $p p \rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{0}_j\rightarrow 4\mu \ 2[\widetilde{\chi }^0_1]_{displaced}$

• (5) $p p \rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{0}_j\rightarrow 4\nu \ 2[\widetilde{\chi }^0_1]_{displaced}.$

Here and in the following the indices i, j and k run through the chargino and neutralino mass eigenstates in the combinations shown in Fig. 11.

Fig. 11

Production of chargino–neutralino pair decaying to left muon-sneutrino, which in turn decays to a long-lived Bino giving rise to a displaced signal

Finally, the displaced binos will decay through an off-shell W mediated by a diagram including the RPV mixing bino-neutrino. Among the possible decays, the five relevant channels are

• (a) $\widetilde{\chi }^0_1\rightarrow 2e + \nu$

• (b) $\widetilde{\chi }^0_1\rightarrow \mu e + \nu$

• (c) $\widetilde{\chi }^0_1\rightarrow 2\mu + \nu$

• (d) $\widetilde{\chi }^0_1\rightarrow qq' + \mu$

• (e) $\widetilde{\chi }^0_1\rightarrow qq' + e$

where each of the 5 channels constitutes a different signal. The ATLAS search found no candidate events in any of the signal regions, which are defined to be background free. Hence any point predicting more than 3 events in any of the signal regions corresponding to the aforementioned channels will be excluded at the 95% confidence level.

We follow the prescription of Refs. [40, 41] for recasting the ATLAS 8 TeV search, but adding to the analysis also the channels corresponding to the decays $\widetilde{\chi }^0_1\rightarrow qq'\ell$, and without considering the optimization of the triggers requirements proposed in those works. The number of displaced vertices corresponding to each channel is calculated as described below and summarized in Eq. (25). We extract the displaced vertex selection efficiency from the plots stating an upper limit on the number of LLP decays provided by ATLAS. Unlike the case studied in Refs. [40, 41], the LLP will be produced here with different expected boosts depending on the mass gap $m_{\widetilde{\chi }^0_2}-m_{\widetilde{\chi }^0_1}$. This is solved using an interpolation between the values extracted for the different lines in the figures of the ATLAS analysis, where the boost factors of the LLP in our proposed model as well as in the benchmark scenarios proposed by ATLAS are estimated according to

$$\begin{aligned} \gamma =\left( 1+\frac{(m_{\widetilde{\chi }^0_2}^2-m_{\widetilde{\chi }^0_1}^2)^2}{4m_{\widetilde{\chi }^0_2}^2m_{\widetilde{\chi }^0_1}^2}\right) ^{1/2}. \end{aligned}$$

(24)

In addition, the efficiency passing the trigger selection requirements is simulated for a sample of points with masses $m_{\widetilde{\chi }^0_2}\in [60,700]~\text {GeV}$ and $m_{\widetilde{\chi }^0_1}\in [60,350]~\text {GeV}$, and the mass of the left muon-sneutrinos considered to be in the middle of both. Events are generated using MadGraph5_aMC@NLO 2.6.7 [103] and PYTHIA 8.243 [104] and we use DELPHES v3.4.2 [105] for the detector simulation. For each point of the parameter space, the value of the trigger efficiency is calculated using a linear interpolation between the points simulated as described before. For the points where the mass $m_{\widetilde{\chi }^0_2}$ is above 700 GeV we use the corresponding upper simulated value, since the efficiency saturates the upper value around this mass.

The number of displaced vertices detectable for each channel is then calculated as

$$\begin{aligned} N^{DV}_{X}= & {} {\mathcal {L}}\times \left\{ \sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{\pm }_j)\right. \nonumber \\&\times \left[ \epsilon ^T_{1X} \times \text {BR}(\widetilde{\chi }^0_i \rightarrow \mu \widetilde{\mu })\times \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \mu \widetilde{\nu }_{\mu })\right. \nonumber \\&\left. +\epsilon ^T_{1X}\times \text {BR}(\widetilde{\chi }^0_i \rightarrow \mu \widetilde{\mu })\times \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \nu \widetilde{\mu } )\right. \nonumber \\&\left. +\epsilon ^T_{3X} \times \text {BR}(\widetilde{\chi }^0_i \rightarrow \nu \widetilde{\nu }_{\mu } )\times \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \mu \widetilde{\nu }_{\mu } )\right. \nonumber \\&\left. \left. +\epsilon ^T_{3X}\times \text {BR}(\widetilde{\chi }^0_i \rightarrow \nu \widetilde{\nu }_{\mu }) \times \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \nu \widetilde{\mu })\right] \right. \nonumber \\&+\sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^{\pm }_j \widetilde{\chi }^{{\mp }}_j)\times \epsilon ^T_{2X} \nonumber \\&\left. \times \left[ \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \mu \widetilde{\nu }_{\mu }) + \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow \nu \widetilde{\mu })\right] ^2\right. \nonumber \\&+\sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^{0}_i \widetilde{\chi }^{0}_k) \nonumber \\&\times \left. \left[ \epsilon ^T_{2X}\times 2\times \text {BR}(\widetilde{\chi }^0_i \rightarrow \mu \widetilde{\mu })\times \text {BR}(\widetilde{\chi }^0_i \rightarrow \nu \widetilde{\nu }_{\mu })\right. \right. \nonumber \\&+\epsilon ^T_{4X} \times \text {BR}(\widetilde{\chi }^0_i \rightarrow \mu \widetilde{\mu })^2\nonumber \\&\left. \left. \left. +\epsilon ^T_{5X}\times \text {BR}(\widetilde{\chi }^0_i \rightarrow \nu \widetilde{\nu }_{\mu })^2\right] \right. \right\} \nonumber \\&\times \epsilon ^{sel}_{X} \times 2\times \text {BR}(\widetilde{\chi }^0_1\rightarrow X), \end{aligned}$$

(25)

where $\epsilon ^T_{1-5X}$ refers to the trigger efficiency associated to each intermediate chain, (1)–(5), and each final decay of the bino ($X=a,b,c,d,e$). For example, $\epsilon ^T_{1a}$ corresponds to the trigger efficiency when the binos are produced through the channel (1) and decay to electrons and neutrinos as in (a). Also $\epsilon ^{sel}_X$ correspond to the selection efficiency of the displaced vertex originating in the decay of the binos through the channel X.

Concerning this analysis of displaced vertices, let us finally remark that we have used the 8 TeV ATLAS search [51] instead of the more recent 13 TeV one [106], because the former search tests all the possible decay channels of the bino while the latter focuses exclusively on leptonic displaced vertices. Moreover, we will show in Sect. 6.4 that many points with a long-lived bino can be excluded with the 8 TeV analysis, and the remaining points cannot be excluded by the most recent analysis.

On the other hand, as already mentioned the selection requirements defined to identify the displaced vertex by the ATLAS collaboration [51] set a lower bound on the proper decay length of about 1 mm, for which the particle could be detected. However, when the mass of the bino is $m_{\widetilde{B}^0} > rsim 130$ GeV the two-body nature of its decay implies that $c\tau$ becomes smaller than 1 mm. In that case, we can apply ATLAS searches based on the promptly produced leptons in the decay of the heavier chargino–neutralino, as we already did in Sect. 6.1 using the auxiliary material of Ref. [50]. If $c\tau \lesssim 1$mm, a fraction of ${\widetilde{\chi }^0_1}$ will decay with a large impact parameter and the corresponding tracks will be discarded from further analysis in prompt searches. Note also that all our (bino LSP-like) points fulfill $c\tau >0.1$ mm. Thus we can compare the events generated as in Fig. 11, without considering the bino products, with the ATLAS search [50] where signal leptons are required to have $|d_0|/\sigma (d_0) < n$ with $d_0$ the transverse impact parameter relative to the reconstructed primary vertex, $\sigma (d_0)$ its error, and $n=3$ for muons and 5 for electrons. The fraction of LSP decays with impact parameters larger than $d_0$ is then expressed by

$$\begin{aligned} \epsilon =e^{- \frac{\sqrt{2} n \sigma (d_0)}{c\tau \beta \gamma } }, \end{aligned}$$

(26)

where $\sigma (d_0)$ is taken to be 0.03 mm according to [107]. For each point of the parameter space, if the production cross section of the process in Fig. 11 times the result of Eq. (26) is above the upper limit obtained by ATLAS in Ref. [50], the point is regarded as excluded.

Let us finally point out that we have also considered here and in the next subsection, whether the case of the direct production of a smuon pair, with the smuon decaying into a muon and a long lived bino, could produce a significant signal. However, as we will discuss in Sect. 6.4, the points that are not excluded by the analysis described above, have a proper decay length around 1 mm, and it is not possible to exclude them by their smuon-initiated signals either.

6.3 Case (iii) $m_{\tilde{B}^0}< m_{\tilde{W}^0}< m_{\tilde{\nu }_\mu }$

The situation in this case is similar to the one presented in the previous subsection, with the difference in the particles produced in the intermediate decay, as shown in Fig. 12. While in Sect. 6.2 this corresponds in most cases to muons, now the intermediate decay will mainly produce hadrons. The LHC constraints are applied in an analogous way, depending also on the value of the proper decay length, larger or smaller than 1 mm. In the former situation, the number of displaced vertices expected to be detectable at ATLAS is now given by

$$\begin{aligned} N^{DV}_{X}= & {} {\mathcal {L}}\times \left\{ \sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^0_i\ \widetilde{\chi }^{\pm }_j)\right. \nonumber \\&\left. \times \left. \epsilon ^T_{1X} \times \text {BR}(\widetilde{\chi }^0_i \rightarrow Z^{0} \widetilde{\chi }^0_1)\times \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow W^{\pm } \widetilde{\chi }^0_1)\right. \right. \nonumber \\&+ \sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^{\pm }_j \widetilde{\chi }^{{\mp }}_j)\times \epsilon ^T_{2X}\nonumber \\&\times \left[ \text {BR}(\widetilde{\chi }^{\pm }_j \rightarrow W^{\pm }\widetilde{\chi }^0_1)\right] ^2\nonumber \\&\quad \times \sigma _{@8~{\mathrm{TeV}}}(pp\rightarrow \widetilde{\chi }^{0}_i \widetilde{\chi }^{0}_k)\times \epsilon ^T_{4X} \nonumber \\&\left. \times \left[ \text {BR}(\widetilde{\chi }^0_{i,k} \rightarrow Z^{0} \widetilde{\chi }^0_1)\right] ^2 \right\} \nonumber \\&\times \epsilon ^{sel}_{X} \times 2\times \text {BR}(\widetilde{\chi }^0_1\rightarrow X), \end{aligned}$$

(27)

where the efficiencies $\epsilon ^T_{1-4X}$ are calculated again with events simulated based on the new scenario. Note that when ${m_{\widetilde{\chi }^{\pm }/\widetilde{\chi }^0}}< m_{W^{\pm }/Z^0} + m_{\widetilde{B}^0}$ the intermediate BRs correspond to three-body decays. If $c\tau < 1$ mm, a similar analysis as in the previous subsection follows.

Fig. 12

Production of chargino–neutralino pair decaying to a long-lived bino giving rise to a displaced signal

6.4 Results

The points obtained in the scan of Sect. 5, and summarized in Fig. 9, are compatible with experimental data on neutrino and Higgs physics, as well as with flavor observables, and explain the discrepancy of the muon $g-2$. In the previous subsections, we have shown that they present a rich collider phenomenology. Depending on the different masses and orderings of the light SUSY particles of the spectrum, we expect different possible signals at colliders. Then, we have argued that this variety of possible signals can be constrained using LHC searches, and explained the analysis to be carried out.

The results of the computation of the LHC limits imposed on the parameter space of our scenario are presented in Fig. 13, which can be compared with those of Fig. 9. The (green and blue) viable points of Fig. 9 are shown in Fig. 13 with light colors when they are excluded by LHC searches. Processes considered relevant for these searches, such as those initiated by $\widetilde{W}^0 \widetilde{W}^{\pm }$ or $\widetilde{W}^{{\mp }} \widetilde{W}^{\pm }$ production, are expected to decrease their exclusion power with increasing values of $M_2$. This is the case for (sneutrino LSP-like) points in the right part of the plot which are allowed by the analysis of these processes (up to $M_2=920$ GeV). However, at the end of the day most of them turn out to be excluded, as can be seen in Fig. 13, and only a bunch compatible with $\Delta a_{\mu }$ at the 2$\sigma$ level survives with $460\lesssim M_2\lesssim 660$ GeV (and $210 \lesssim m_{\widetilde{\nu }_\mu }\lesssim$ 270 GeV). These values of $M_2$ correspond to bino and wino masses in the ranges about 220–311 GeV and 510–695 GeV, respectively. This extensive exclusion is because of the limits imposed on the higgsino-like chargino pair production, and typically occurs when $M_2>\mu$ and therefore the higgsino is lighter than the wino. Since in our scan we have fixed $\mu \approx 379$ GeV following the discussion of Sect. 4.3, points with $M_2 > rsim 379$ GeV have this hierarchy of masses.

Fig. 13

The same as in Fig. 9, but without showing the red points which are not within the $2\sigma$ cut on $\Delta a_\mu$. The light-green and light-blue colors indicate points that are excluded by LHC searches

Fig. 14

The same as in Fig. 13, but allowing green and blue points not fulfilling the relation $M_2=2M_1$. In addition, points with a larger value of $\mu$ are allowed as discussed in the text. The orange colors represent the latter points in the $2\sigma$ region of $\Delta a_\mu$ in Eq. (1). Light-violet and light-orange colors indicate those points in the $1\sigma$ and $2\sigma$ regions excluded nevertheless by LHC searches

On the other hand, most of the (bino LSP-like) points turn out to be also excluded. For $c\tau>$ 1 mm, i.e. with $152\lesssim M_2\lesssim 283$ GeV, only a few points represented by blue crosses in the figure, with $M_2$ between 260 and 283 GeV and therefore with $c\tau$ close to 1, survive. They have $240 \lesssim m_{\widetilde{\nu }_\mu }\lesssim$ 250 GeV, and their corresponding bino and wino masses are in the ranges about 126–133 GeV and 255–266 GeV, respectively. Similarly, when the proper decay length of the bino LSP is smaller than 1 mm corresponding to $283\lesssim M_2\lesssim 460$ GeV, most of the points are excluded by the constraints from LHC searches discussed in Sects. 6.2 and 6.3 with Eq. (26). Only some points represented by blue triangles in the region of $283\lesssim M_2\lesssim 350$ GeV and $280\lesssim m_{\widetilde{\nu }_\mu }\lesssim$ 410 GeV are still compatible with $\Delta a_{\mu }$ at the 2$\sigma$ level. These values of $M_2$ correspond to bino and wino masses in the ranges about 136–168 GeV and 272–320 GeV, respectively.

The conclusion of this analysis is that LHC searches are very powerful to constrain our scenario. In particular, all the points found compatible with $\Delta a_{\mu }$ at the 1$\sigma$ level turn out to be excluded, and not many regions of points compatible at the 2$\sigma$ level survive. Fortunately, this is not the end of the story. The GUT-inspired low-energy assumption $M_2=2M_1$ was very useful to optimize the number of parameters used in the scan, given the demanding computing task. Nevertheless, we will be able to explore other interesting regions of the parameter space breaking this relation, and using essentially the points already got from the previous scan.

As already explained, neutrino physics depends mainly on the parameter M defined in Eq. (6). Thus for a given value of M reproducing the correct neutrino (and Higgs) physics, one can get different pairs of values of $M_1$ and $M_2$ with the same good property, without essentially modifying the values of the other parameters. In addition, given the left muon-sneutrino mass corresponding to each one of these points, one can obtain more good points just varying $T_{\nu _2}$, since this parameter does not affect neutrino/Higgs physics. The result of this strategy can be seen in Fig. 14, where the previous blue points of Fig. 13 in the $2\sigma$ region of $\Delta a_\mu$ are shown together with the new blue points obtained. In addition points in the $1\sigma$ region shown with green color are obtained. Given that the GUT relation between bino and wino masses is not imposed, many bino LSP-like points represented by crosses and triangles become now unconstrained by LHC searches. Similarly, more sneutrino LSP-like points represented by dots are also allowed, since more sneutrino masses have been explored for given values of the rest of parameters.

On the other hand, it is worth noticing that an important constraint on sneutrino LSP-like points in Fig. 13 was due to higgsino-like chargino pair production, with the higgsino as the NLSP when $M_2>\mu$. Nevertheless, this originates from the fact that the $\mu$ parameter used in our scan was fixed to 379 GeV in order to reproduce Higgs physics, constraining therefore mainly points with values of $M_2>379$ GeV. As already pointed out above, this is nothing more than an artifact of our calculation, since many different values of $\mu$ are possible reproducing the correct Higgs physics [59], and in particular larger ones. Thus, in Fig. 14 we have also included points with $\mu =3 \lambda \frac{v_{R}}{\sqrt{2}}\approx 800$ GeV, in order to allow the events initiated by higgsinos to pass the selection cuts. To carry it out, we have modified the values of $\lambda$ and $v_R$ in Table 3, using $\lambda =0.126$ and $v_R=3000$ GeV. Other benchmark parameters relevant for Higgs physics have to be modified such as $\kappa =0.36$, $-T_{\kappa } =150$ GeV, $T_{\lambda }=1000$ GeV, $-T_{u_{3}}=4375$, $m_{\widetilde{Q}_{3L},\widetilde{u}_{3R}}= 2500$ GeV, $M_3 = 3500$ GeV, and $m_{\widetilde{Q}_{1,2L}}, m_{\widetilde{u}_{1,2R}}, m_{\widetilde{d}_{1.2,3R}}, m_{\widetilde{e}_{1,2,3R}}= 1500$ GeV. In Table 2 we have also modified $\tan \beta \in (25, 35)$. Concerning the left muon-sneutrino mass we have slightly increased the upper limit of $-T_{\nu _{2}}$ up to $4.4\times 10^{-4}$, and to obtain slightly smaller chargino masses we have decreased the lower limit of $M_2$ up to 100 GeV. The effect of the larger value of the higgsino mass, together with the breaking of the GUT relation between wino and bino masses, give rise to more points in the parameter space fulfilling not only the value of $\Delta a_\mu$ in Eq. (1) but also the LHC bounds. These points are shown with orange colors in Fig. 14. For some of the orange dots in the range $600\lesssim M_2\lesssim 700$ GeV we have allowed points with the hierarchy $M_2<M_1$, since it is not relevant for the LHC constraints used.

Therefore, although LHC searches can be important to constrain the parameter space of the $\mu \nu \mathrm{SSM}$, we have obtained that significant regions fulfilling these constraints can be found, explaining at the same time the muon $g-2$ data. The $1\sigma$ region is shown with green color in Fig. 14, and the $2\sigma$ with blue and orange colors.

7 Conclusions and outlook

We have analyzed within the framework of the $\mu \nu \mathrm{SSM}$, regions of its parameter space that can explain the $3.5\sigma$ deviation of the measured value of the muon anomalous magnetic moment with respect to the SM prediction. We have shown that the $\mu \nu \mathrm{SSM}$ can naturally produce light left muon-sneutrinos and electroweak gauginos, that are consistent with Higgs and neutrino data as well as with flavor observables such as B and $\mu$ decays. The presence of these light sparticles in the spectrum is known to enhance the SUSY contribution to $a_\mu$, and thus it is crucial for accommodating the discrepancy between experimental and SM values.

We have obtained this result sampling the $\mu \nu \mathrm{SSM}$ in order to reproduce the latest value of $\Delta a_\mu$, simultaneously achieving the latest Higgs and neutrino data. We have found significant regions of the parameter space with these characteristics. Then, we have studied the constraints from LHC searches on the solutions obtained. The latter have a rich collider phenomenology with the possibilities of left muon-sneutrino, or bino-like neutralino, as LSP. In particular, we found that multi-lepton $+$ MET searches [50, 51] can probe some regions of our scenario through chargino–chargino, chargino–neutralino and neutralino–neutralino production.

The final result is that significant regions of the parameter space of the $\mu \nu \mathrm{SSM}$ are compatible with the value of $\Delta a_\mu$ and LHC constraints. They correspond to the ranges $120\lesssim m_{\widetilde{\nu }_\mu }\lesssim 620$ GeV, $120\lesssim M_1\lesssim 2200$ GeV and $200\lesssim M_2\lesssim 900$ GeV. These values of $M_1$ and $M_2$ correspond to bino and wino masses in the ranges about 120–2200 GeV and 200–930 GeV, respectively. Figure 14 summarizes this result about muon $g-2$, which can have important implications for future LHC searches. If the deviation with respect to the SM persists in the future, then this prediction of the $\mu \nu \mathrm{SSM}$ can be used for pinning down the mass of the left muon-sneutrino, as well as for narrowing down the mass scale for a potential discovery of electroweak gauginos.

Let us finally discuss briefly several other possibilities for the analysis of the muon $g-2$ in the $\mu \nu \mathrm{SSM}$ that are worth investigating in the future. Note first that we have only scanned the model over the parameters controlling neutrino/sneutrino physics, fixing those controlling Higgs physics. Although this simplification was necessary to relax our demanding computing task, it also indicates that more solutions could have been found in other regions of the parameters relevant for Higgs physics [59]. Actually, a similar comment applies to the parameters controlling neutrino physics where the scan was carried out. We worked with a solution with diagonal neutrino Yukawas fulfilling in a simple way neutrino physics through the dominance of the gaugino seesaw, but if a different hierarchy of Yukawas (and sneutrino VEVs) is considered, or off-diagonal Yukawas are allowed, more solutions could have been found. Thus, the result summarized in Fig. 14 can be considered as a subset of all the solutions that could be obtained if a general scan of the parameter space of the model is carried out. Besides, we could have a significant neutralino-smuon contribution to muon $g-2$ to be added to the chargino-sneutrino one, allowing for a light right smuon mass. In our scan we used this mass equal to 1000 (and 1500) GeV for simplicity, but smaller values are possible through light soft masses, increasing therefore this contribution.