Quadruply charmed dibaryons as heavy quark symmetry partners of the DDK bound state

Abstract

Both unitary chiral theories and lattice QCD simulations show that the DK interaction is attractive and can form a bound state, namely, $D^*_{s0}(2317)$. Assuming the validity of the heavy antiquark–diquark symmetry, the $\Xi _{cc}{\bar{K}}$ interaction is the same as the DK interaction, which implies the existence of a $\Xi _{cc}{\bar{K}}$ bound state with a binding energy of $49-64$ MeV. In this work, we study whether a $\Xi _{cc}\Xi _{cc}{\bar{K}}$ three-body system binds. The $\Xi _{cc}\Xi _{cc}$ interaction is described by exchanging $\pi$, $\sigma$, $\rho$, and $\omega$ mesons, with the corresponding couplings related to those of the NN interaction via the quark model. We indeed find a $\Xi _{cc}\Xi _{cc}{\bar{K}}$ bound state, with quantum numbers $J^P=0^-$, $I=\frac{1}{2}$, $S=1$ and $C=4$, and a binding energy of 80–118 MeV. With the same formalism, we find that the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system also binds, yielding a $I(J^P)=\frac{1}{2}(0^+)$ state and a $\frac{1}{2}(1^+)$ state with binding energies of 56–68 MeV and 56–67 MeV respectively. As a byproduct, we show the existence of a $NN{\bar{K}}$ state with a binding energy of 35–43 MeV, consistent with the results of other theoretical works and experimental data, which serves as a consistency check on the predicted $\Xi _{cc}\Xi _{cc}{\bar{K}}$ bound state.

1 Introduction

In 2017, the LHCb Collaboration reported the observation of a doubly charmed baryon, the $\Xi _{cc}^{++}$ [1]. Its quark content is ccu, where it is interesting to notice that we expect the cc charmed quark pair to be tightly packed together. The theoretical reason behind this is heavy antiquark–diquark symmetry (HADS) [2], a type of heavy-quark symmetry stating that a heavy-quark pair behaves approximately as a heavy antiquark. In practical terms what this means is that the structure of the doubly heavy baryon is the same as the one of a heavy antimeson, i.e. the wave function of the light-quark within the $\Xi _{cc}^{(*)}$ baryon is the same as that in the $\bar{D}^{(*)}$ meson (modulo corrections owing to the finite charm quark mass). Consequently, HADS also implies that many of the findings related to ${D}^{(*)}$ mesons are likely to apply to $\Xi _{cc}^{(*)}$ baryons. For instance, if there are DK [3,4,5,6] and DDK [7,8,9] bound states the same is expected to happen to the $\Xi _{cc} {\bar{K}}$ and $\Xi _{cc} \Xi _{cc} {\bar{K}}$ systems. This last system will be the subject of the present manuscript.

The existence of a DK bound state is usually argued on the basis of the experimental location of the $D_{s0}^*(2317)$ [10,11,12]. The mass of this resonance is excessively low to be accommodated as a $c {\bar{s}}$ state in the quark-model. Yet from chiral symmetry we expect the DK interaction to be really strong and attractive, leading to the natural explanation that the $D_{s0}^*(2317)$ is a bound state [3,4,5,6]. Indeed the attraction in the DK system has been repeatedly shown to be strong enough to form this state [13,14,15,16,17,18]. Now, if we consider HADS, then the binding of the DK system implies that the $\Xi _{cc}{\bar{K}}$ system should bind too, a conclusion which has been pointed out in a series of theoretical works. For instance, Ref. [19] predicts an isoscalar $\Xi _{cc}{\bar{K}}$ bound state at about $60 \pm 20\,\mathrm{MeV}$ below threshold. Reference [20] considers the $\Xi _{cc}{\bar{K}}$-$\Omega _{cc}\eta$ coupled system, for which binding happens at about $150\,\mathrm{MeV}$ below threshold. In Ref. [21] the authors calculated the $\Xi _{cc}{\bar{K}}$ scattering length to be $2.15\,\mathrm{fm}$, which being positive (and provided that the system is attractive) indicates the existence of a bound state. In Ref. [22], in addition to the next-to-leading order chiral potentials, the P-wave excitation between the two heavy quarks was taken into account as a dynamical degree of freedom, a $\Xi _{cc}{\bar{K}}$ bound state with a binding energy of 50 MeV was predicted.

The bottom-line is that the existence of a $\Xi _{cc}{\bar{K}}$ bound state is really likely, at least if HADS breaking is not too large. This immediately raises the intriguing question of whether there exists a $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer. The reasons why such a trimer is probable are HADS and the theoretical predictions of a DDK bound state [7,8,9, 23]. It is also interesting to notice that the probable mechanism responsible for the formation of the DDK and $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimers is the strong Weinberg–Tomozawa (WT) term in the DK and $\Xi _{cc} {\bar{K}}$ subsystems. ¹ This feature is shared with the $N{\bar{K}}$ system, which is usually thought to be the most important component of the $\Lambda (1405)$ wave function and which also leads to the formation of $NN{\bar{K}}$ bound states, as has been extensively studied in both theory [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] and experiment [43,44,45,46,47,48,49,50], with the later supporting the existence of this trimer. Motivated by these facts, in this manuscript we will explore the three-body $\Xi _{cc}\Xi _{cc}{\bar{K}}$ as well as the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ systems, which we conclude to be likely to bind.

The article is organized as follows: in Sect. 2, we explain the $\Xi _{cc}{\bar{K}}$ and $\Xi _{cc}\Xi _{cc}$ interactions. In Sect. 3 we construct the three-body wave functions and solve the corresponding Schrödinger equation for the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system using the Gaussian expansion method (GEM). In Sect. 4, we explain how the Thomas collapse affects the cutoff dependence of the binding energy of the $\Xi _{cc}\Xi _{cc}\bar{K}$ trimer. In Sect. 5, we present our predictions and discuss the theoretical uncertainties associated with them. Finally, we summarize our results in Sect. 6.

2 Two-body interactions

Here we will explain in detail how to derive the $\Xi _{cc}{\bar{K}}$ and $\Xi _{cc}\Xi _{cc}$ interactions. For the case of the $\Xi _{cc}{\bar{K}}$ system the most important part of the interaction is given by the Weinberg–Tomozawa term, which happens to be identical to that of the DK system owing to HADS and chiral symmetry. For the $\Xi _{cc} \Xi _{cc}$ system we will resort to the one boson exchange (OBE) model, where the non-relativistic potential between the two baryons is determined by the exchange of a few light mesons (the pion, the sigma, the rho and the omega). For determining the coupling constants of these light mesons to the doubly-charmed baryons we will resort to HADS and the information we can deduce from the DD two charmed-meson system and the quark model.

2.1 0$\left( \frac{1}{2}^-\right)$ $\Xi _{cc}{\bar{K}}$ potential

The most important contribution to the $\Xi _{cc}{\bar{K}}$ interaction is the Weinberg–Tomozawa term between the kaon and the doubly charmed baryon, which in a non-relativistic normalization reads

$$\begin{aligned} V_{WT}(\vec {q}) = - \frac{C_{WT}(I)}{2 f_{\pi }^2}, \end{aligned}$$

(1)

with $f_{\pi } \simeq 130\,\mathrm{MeV}$ and $C_{WT}(0) = 2$, $C_{WT}(1) = 0$ for the isoscalar and isovector channels, respectively. This coincides with the standard half-relativistic (relativistic kaon and non-relativistic baryon) normalization $C_{WT}(I) (\omega _K + \omega _K') / 2f_{\pi }^2$. This potential is exactly the same one as for the DK system as a consequence of two independent facts: the universality of the WT term (and the fact that D and $\Xi _{cc}$ belong to the $\bar{3}$ and 3 representations of SU(3)-flavor) and HADS, which also implies the same interaction in both systems.

The Fourier-transform of the previous potential in coordinate space is

$$\begin{aligned} V_{WT}(\vec {r}) = - \frac{C_{WT}(I)}{2 f_{\pi }^2}\,\delta ^{(3)}(\vec {r}) , \end{aligned}$$

(2)

which is singular and requires regularization. For that purpose we will choose a Gaussian regulator of the type

$$\begin{aligned} V_{WT}(\vec {r}) = - \frac{C_{WT}(I)}{2 f_{\pi }^2}\, \frac{e^{-(r/R_c)^2}}{\pi ^{3/2} R_c^3}, \end{aligned}$$

(3)

where $R_c$ is a coordinate space cutoff. However the previous expression is still problematic, as the prediction of a bound $\Xi _{cc} {\bar{K}}$ state and its binding energy depends on the cutoff. If there is an experimentally known bound state, then it is easy to choose the cutoff in order to reproduce that bound state. Though this is not the case for the $\Xi _{cc} {\bar{K}}$, it happens that the $D_{s0}^*(2317)$ is suspected to be a DK bound state. From this we can set the cutoff in the DK system, which, owing to HADS, should be the same cutoff as in the $\Xi _{cc} {\bar{K}}$ system.

But there is the more powerful approach of fully renormalizing the $\Xi _{cc} {\bar{K}}$/DK interaction, which is what we will do here. For that, we allow the strength of the WT term to vary with the cutoff

$$\begin{aligned} V(\vec {r}) = \hat{C}(R_c)\,\frac{e^{-(r/R_c)^2}}{\pi ^{3/2} R_c^3}, \end{aligned}$$

(4)

where for every value of $R_c$ we determine $\hat{C}(R_c)$ by reproducing the $D_{s0}^*(2317)$ as a DK bound state. After this we can predict the binding energy of the $\Xi _{cc} {\bar{K}}$ system.² In addition to this, we can also modify the previous potential with a shorter-range contribution as follows

$$\begin{aligned} V_{WT}(\vec {r})= & {} \hat{C}(R_c)\,\frac{e^{-(r/R_c)^2}}{\pi ^{3/2} R_c^3} + \hat{C}_S\,\frac{e^{-(r/R_S)^2}}{\pi ^{3/2} R_S^3} \nonumber \\= & {} C(R_c)\,e^{-(r/R_c)^2} + C_S\,e^{-(r/R_S)^2}, \end{aligned}$$

(7)

where we take $R_S < R_c$ and $C_S > 0$ (i.e. repulsive) with $|C_S| > |C(R_c)|$. Notice that we also define the couplings $C(R_c)$ and $C_S$, which are equivalent to $\hat{C}(R_c)$ and $\hat{C}_S$ but more convenient to use. The purpose of this modification is to take into account the fact that the subleading order corrections to the WT term for the DK interaction are repulsive in nature (with the same thing happening in the $\Xi _{cc} {\bar{K}}$ system owing to HADS) [14]. For concreteness we will take $R_c =$ 0.5–2.0$\,\mathrm{fm}$ and $R_S = 0.1\,\mathrm{fm}$. For $C_S$ we will consider two possibilities: $C_S = 0$ (i.e. we ignore the existence of subleading order corrections) and ${C}_S = 1\,\mathrm{GeV}$ (to exaggerate the strength of these corrections). The binding energy we predict for the $\Xi _{cc} {\bar{K}}$ state lies in the range $B_2 =$ (50–60)$\,\mathrm{MeV}$ and are almost independent of $C_S$. Concrete results for each cutoff can be checked in Table 2, which we will discuss later on.

In addition to the strong force, the $\Xi _{cc} {\bar{K}}$ system also receives contributions from the electromagnetic force if the antikaon happens to be charged (the $\Xi _{cc}$ is always charged, with its particle states being $\Xi _{cc}^+$ or $\Xi _{cc}^{++}$). The two particle components of the $I=0$ channel in which the $\Xi _{cc} {\bar{K}}$ interaction is expected to be stronger are

$$\begin{aligned} | \Xi _{cc} {\bar{K}} (I=0) \rangle = \frac{1}{\sqrt{2}}\, \left[ | \Xi _{cc}^{+} {\bar{K}}^0 \rangle + | \Xi _{cc}^{++} {K}^- \rangle \right] . \end{aligned}$$

(8)

For each of these components the Coulomb force reads

$$\begin{aligned} V^C_{\Xi _{cc}^{+} {\bar{K}}^{0}}(r)= & {} 0 , \end{aligned}$$

(9)

$$\begin{aligned} V^C_{\Xi _{cc}^{++} K^{-}}(r)= & {} -2 \frac{\alpha }{r} , \end{aligned}$$

(10)

or, equivalently, if we write it with isospin operators

$$\begin{aligned} V^C_{\Xi _{cc} {\bar{K}}}(r)= \frac{\alpha }{r}\,\frac{(\tau _{z,1} +3)}{2}\, \frac{(-1+\tau _{z,2})}{2} , \end{aligned}$$

(5)

with $\tau _{z,1}$ and $\tau _{z,2}$ the third component of the isospin operator for the doubly charmed baryon and antikaon, respectively. The problem is that the Coulomb force breaks isospin symmetry, which can be dealt with in two ways. The simplest one is to average the Coulomb force over the particle components of the $I=0$ state

$$\begin{aligned} \langle \Xi _{cc} {\bar{K}} (I=0) | V^C(r) | \Xi _{cc} {\bar{K}} (I=0) \rangle = - \frac{\alpha }{r} . \end{aligned}$$

(11)

The other possibility is to consider the $| \Xi _{cc}^{+} {\bar{K}}^0 \rangle$ and $| \Xi _{cc}^{++} {K}^- \rangle$ components separately as channels 1 and 2, in which case we can write the full potential as

$$\begin{aligned} V(r) = V_{WT}(r)\,\frac{1}{2} \begin{pmatrix} 1 &{} 1 \\ 1 &{} 1 \end{pmatrix} - \frac{\alpha }{r} \begin{pmatrix} 0 &{} 0 \\ 0 &{} 2 \end{pmatrix} . \end{aligned}$$

(12)

In this work we will choose the first option, the one described by Eq. (11), as this will greatly simplify the formalism required to do the calculations, particularly once we consider the three-body system.

2.2 The $\Xi _{cc}\Xi _{cc}$ potential in the one boson exchange model

In the OBE model the interaction between two hadrons is described in terms of the exchange of a series of light mesons, which most commonly include the pion ($\pi$), sigma ($\sigma$), rho ($\rho$) and omega ($\omega$), but sometimes a few more bosons in its more sophisticated incarnations. Indeed the OBE model has provided one of the most quantitatively successful description of the nuclear forces [66, 67] and in principle there is nothing impeding its application to other two-hadron systems. Regarding hadronic molecules, it is interesting to notice that the original speculations about their existence were based on the OBE model [68], which later has been widely used for predicting or explaining molecular states [69,70,71,72,73,74].

The particular version of the OBE model we will use is the one developed in Ref. [75] for the $D\bar{D}$ and DD family of charmed meson molecules, which in turn can be related to the $\Xi _{cc} \Xi _{cc}$ case via HADS. The most important difference of Ref. [75] with previous implementations of the OBE model for heavy hadron molecules is the inclusion of a few of the ideas of the renormalized OBE model of Ref. [76]. In particular we partially renormalize the OBE model, by which we mean the following: the OBE model contains a form factor and a cutoff $\Lambda$, where we determine the cutoff $\Lambda$ from the condition of reproducing a known molecular state. The molecular state chosen is the X(3872), of which there is evidence that it might be a $D^*\bar{D}$ molecule with $J^{PC} = 1^{++}$ and isospin $I=0$. For the case of a monopolar form factor the resulting cutoff is $\Lambda _X = 1.01^{+0.19}_{-0.10}\,\mathrm{GeV}$.

We will not explain in detail here how to derive the OBE potential for the general $\Xi _{cc}^{(*)} \Xi _{cc}^{(*)}$ system from HADS and the potential developed in Ref. [75] for the $D^{(*)} D^{(*)}$ system. Instead we will simply indicate how to do it, where the starting point is the definitions of the charmed meson and doubly charmed baryon superfields

$$\begin{aligned} H_c= & {} \frac{1}{\sqrt{2}}\left[ D + \vec {\sigma } \cdot \vec {D}^* \right] \quad , \quad \vec {T}_{cc} = \frac{1}{\sqrt{3}} \vec {\sigma }\,\Xi _{cc} + \vec {\Xi }^*_{cc} , \end{aligned}$$

(13)

which group the D, $D^*$ meson ($\Xi _{cc}$, $\Xi _{cc}^*$ baryon) fields into a single superfield with good properties with respect to rotations of the heavy quark spin. For implementing HADS there are several possibilities, of which we briefly explain two. One is to group the two superfields $H_c$ and $T_{cc}$ into a new superfield $\mathcal {H}_c$ which is invariant under HADS. The other is to simply notice that the previous procedure at the end amounts to make the following substitutions in the Lagrangians:

$$\begin{aligned} \mathrm{Tr}\left[ H_c^\dagger \mathcal {O} H_c \right] \rightarrow T_{cc}^{\dagger } \, \mathcal {O} \, T_{cc} , \end{aligned}$$

(14)

with $\mathcal {O}$ some arbitrary spin operator acting on the superfields. If we do this with the OBE Lagrangian of Ref. [75] we will be able to derive the potentials we will write down below.

The outcome of the previous procedure for the particular case of the $\Xi _{cc} \Xi _{cc}$ system is

$$\begin{aligned} V_\mathrm{OBE}= & {} V_{\pi } + V_{\sigma } + V_{\rho } + V_{\omega } , \end{aligned}$$

(15)

where the contributions from the $\pi$, $\sigma$, $\rho$ and $\omega$ read

$$\begin{aligned} V_{\pi }(\vec {r})= & {} \vec {\tau }_1 \cdot \vec {\tau }_2\,\frac{g^2}{6 f_{\pi }^2}\,\Bigg [ - \frac{1}{9}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2\,m_{\pi }^3\, d\left( m_\pi r, \frac{\Lambda }{m_{\pi }}\right) \nonumber \\&\qquad + \frac{1}{9}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2\,m_{\pi }^3\, W_Y\left( m_{\pi } r, \frac{\Lambda }{m_{\pi }}\right) \nonumber \\&\qquad + \frac{1}{9}\,S_{12}(\vec {r})\,m_{\pi }^3\, W_T\left( m_{\pi } r, \frac{\Lambda }{m_{\pi }}\right) \Bigg ] , \end{aligned}$$

(16)

$$\begin{aligned} V_{\sigma }(\vec {r})= & {} -{g_{\sigma }^2}\,m_{\sigma }\, W_Y\left( m_{\sigma } r, \frac{\Lambda }{m_{\sigma }}\right) , \end{aligned}$$

(17)

$$\begin{aligned} V_{\rho }(\vec {r})= & {} \vec {\tau }_1 \cdot \vec {\tau }_2\,\Bigg [ {g_{\rho }^2}\,m_{\rho }\,W_Y\left( m_{\rho } r, \frac{\Lambda }{m_{\rho }}\right) \nonumber \\&\qquad + \frac{f_{\rho }^2}{4 M^2}\,\Bigg ( -\frac{2}{27}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2 \, m_{\rho }^3 \, W_Y\left( m_{\rho } r, \frac{\Lambda }{m_{\rho }}\right) \nonumber \\&\qquad +\frac{2}{27}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2 \, m_{\rho }^3 \, W_Y\left( m_{\rho } r, \frac{\Lambda }{m_{\rho }}\right) \nonumber \\&\qquad -\frac{1}{27}\,S_{12}(\hat{r})\, m_{\rho }^3 \, W_T\left( m_{\rho } r, \frac{\Lambda }{m_{\rho }}\right) \Bigg ) \, \Bigg ] , \end{aligned}$$

(18)

$$\begin{aligned} V_{\omega }(\vec {r})= & {} {g_{\omega }^2}\,m_{\omega }\,W_Y\left( m_{\omega } r, \frac{\Lambda }{m_{\omega }}\right) \nonumber \\&\qquad \times \frac{f_{\omega }^2}{4 M^2} \Bigg ( -\frac{2}{27}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2 \, m_{\omega }^3\,d\left( m_{\omega } r, \frac{\Lambda }{m_{\omega }}\right) \nonumber \\&\qquad +\frac{2}{27}\,\vec {\sigma }_1 \cdot \vec {\sigma }_2 \, m_{\omega }^3 \, W_Y\left( m_{\omega } r, \frac{\Lambda }{m_{\omega }}\right) \nonumber \\&\qquad -\frac{1}{27}\,S_{12}(\hat{r})\, m_{\omega }^3 \, W_T\left( m_{\omega } r, \frac{\Lambda }{m_{\omega }}\right) \Bigg ) , \end{aligned}$$

(19)

where for a monopolar form factor the functions d, $W_Y$ and $W_T$ take the form

$$\begin{aligned} d(x, \lambda )= & {} \frac{(\lambda ^2 - 1)^2}{2 \lambda }\, \frac{e^{-\lambda x}}{4 \pi } , \end{aligned}$$

(20)

$$\begin{aligned} W_Y(x, \lambda )= & {} W_Y(x) - \lambda W_Y(\lambda x) \nonumber \\&- \frac{(\lambda ^2 - 1)}{2 \lambda }\,\frac{e^{-\lambda x}}{4 \pi } , \end{aligned}$$

(21)

$$\begin{aligned} W_T(x, \lambda )= & {} W_T(x) - \lambda ^3 W_T(\lambda x) \nonumber \\&- \frac{(\lambda ^2 - 1)}{2 \lambda }\,\lambda ^2\, \left( 1 + \frac{1}{\lambda x} \right) \,\frac{e^{-\lambda x}}{4 \pi } . \end{aligned}$$

(22)

Fig. 1

Three permutations of the Jacobi coordinates for the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system

For the coupling constants we follow Ref. [75] and take $g = 0.60$, $g_{\sigma } = 3.4$, $g_{\rho } = g_{\omega } = 2.6$, $f_{\rho } = f_{\omega } = g_{\omega } \kappa _{\omega }$, $\kappa _{\omega } = 4.5$ and $M = 1867\,\mathrm{MeV}$.

Finally we have to include the Coulomb piece, which written in the isospin basis reads

$$\begin{aligned} V^C_{\Xi _{cc} \Xi _{cc}}(r)= \frac{\alpha }{r}\,\frac{(\tau _{z,1} +3)}{2}\,\frac{(\tau _{z,2} +3)}{2} . \end{aligned}$$

(23)

If we consider the $S=0$ (singlet) S-wave $\Xi _{cc} \Xi _{cc}$ molecule, there are three possible isospin states corresponding to the $\Xi _{cc}^+ \Xi _{cc}^+$, $\Xi _{cc}^+ \Xi _{cc}^{++}$ and $\Xi _{cc}^{++} \Xi _{cc}^{++}$ systems. If we consider the $S=1$ (triplet) case, this corresponds to $\Xi _{cc}^+ \Xi _{cc}^{++}$ and a Coulomb potential

$$\begin{aligned} V^C_{\Xi _{cc} \Xi _{cc}}(r; S=1, I = 0) = 2\,\frac{\alpha }{r}. \end{aligned}$$

(24)

Concrete calculations with the previous parameters indicate that there is no singlet bound state but that a triplet bound state – the charming deuteron – will bind for $\Lambda _S \ge 994\,\mathrm{MeV}$ without Coulomb and $\Lambda _C \ge 1112\,\mathrm{MeV}$ with Coulomb, consistent with the previous prediction of Ref. [77] .

3 Gaussian expansion method

Once we have determined all the relevant two-body interactions, we are ready to explore the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ three-body system. For this we will use the Gaussian Expansion Method (GEM) [78, 79], which is an efficient method to solve few-body systems. The starting point is the Schödinger equation

$$\begin{aligned} H\Psi _{JM}^{total}=E\Psi _{JM}^{total}, \end{aligned}$$

(25)

with the Hamiltonian

$$\begin{aligned} \hat{H} = \sum _{i=1}^{3} \frac{p_i^2}{2m_i}-T_{c.m.} + V_{\Xi _{cc}{\bar{K}}}(r_1) + V_{\Xi _{cc}{\bar{K}}}(r_2) + V_{\Xi _{cc}\Xi _{cc}}(r_3), \end{aligned}$$

(26)

where $T_{c.m.}$ is the kinetic energy of the center of mass and V(r) is the potential between the two relevant particles. The three possible permutations of the Jacobi coordinates for the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system are depicted in Fig. 1.

The total wave function can be expressed as the sum of the amplitudes of the three re-arrangement channels ($c = 1-3$), i.e. the permutations shown in Fig. 1, which we write as

$$\begin{aligned} \Psi _{JM}^{total}= \sum _{c,\alpha }C_{c,\alpha }\Psi _{JM,\alpha }^{c}(\mathbf {r}_c,\mathbf {R}_c), \end{aligned}$$

(27)

with $\mathbf {r}_c$ and $\mathbf {R}_c$ the Jacobi coordinates in channel c.

As can be appreciated, the wave function is expanded in a series in terms of $\alpha =\{nl,NL,\Lambda ,tT\}$ (explained below), with $C_{c,\alpha }$ the expansion coefficients.

Here l and L are the orbital angular momentum for the coordinate r and R, t is the isospin of the two-body subsystem in each channel, $\Lambda$³ and T are the total orbital angular momentum and isospin, n and N are the numbers of gaussian basis functions corresponding to coordinates r and R, respectively.

Considering that the two baryons are identical, the total wave function should be antisymmetric with respect to the exchange of the two $\Xi _{cc}$ baryons, which requires

$$\begin{aligned} P_{12} \Psi _{JM}^{total}= -\Psi _{JM}^{total}, \end{aligned}$$

(28)

where $P_{12}$ is the exchange operator of particles 1 and 2. The wave function of each channel has the following form

$$\begin{aligned} \Psi _{JM,\alpha }^{c}(\mathbf {r}_c,\mathbf {R}_c) = H_{T,t}^c\otimes [\Phi _{lL,\Lambda }^c(\mathbf {r}_c,\mathbf {R}_c)]_{JM}, \end{aligned}$$

(29)

where $H_{T,t}^c$ is the isospin wave function, and $\Phi _{lL,\Lambda }^c$ the spacial wave function. The isospin wave function in each channel reads as

$$\begin{aligned} H_{T,t}^{c=1}&= [[\eta _{\frac{1}{2}}(\Xi _{cc}^2)\eta _{\frac{1}{2}}({\bar{K}}^3)]_{t_1} \eta _{\frac{1}{2}}(\Xi _{cc}^1)]_{\frac{1}{2}}, \nonumber \\ H_{T,t}^{c=2}&= [[\eta _{\frac{1}{2}}(\Xi _{cc}^1)\eta _{\frac{1}{2}}({\bar{K}}^3)]_{t_2} \eta _{\frac{1}{2}}(\Xi _{cc}^2)]_{\frac{1}{2}},\nonumber \\ H_{T,t}^{c=3}&= [[\eta _{\frac{1}{2}}(\Xi _{cc}^1)\eta _{\frac{1}{2}}(\Xi _{cc}^2)]_{t_3} \eta _{\frac{1}{2}}({\bar{K}}^3)]_{\frac{1}{2}}. \end{aligned}$$

(30)

The orbital wave function $\Phi _{lL,\Lambda }^c$ is given in terms of the Gaussian basis functions

$$\begin{aligned} \Phi _{lL,\Lambda }^c(\mathbf {r}_c,\mathbf {R}_c)= & {} [\phi _{n_cl_c}^{G}(\mathbf {r}_c) \psi _{N_cL_c}^{G}(\mathbf {R}_c)]_{\Lambda }, \end{aligned}$$

(31)

$$\begin{aligned} \phi _{nlm}^{G}(\mathbf {r}_c)= & {} N_{nl}r_c^le^{-\nu _n r_c^2} Y_{lm}({\hat{r}}_c), \end{aligned}$$

(32)

$$\begin{aligned} \psi _{NLM}^{G}(\mathbf {R}_c)= & {} N_{NL}R_c^Le^{-\lambda _n R_c^2} Y_{LM}({\hat{R}}_c). \end{aligned}$$

(33)

Here $N_{nl}(N_{NL})$ is the normalization constant of the Gaussian basis and the parameters $\nu _n$ and $\lambda _n$ are given by

$$\begin{aligned} \nu _n&=1/r_n^2,\qquad r_n=r_{min}a^{n-1}\quad (n=1,n_{max}), \nonumber \\ \lambda _N&=1/R_N^2,\quad R_N=R_{min}A^{N-1}\quad (N=1,N_{max}), \end{aligned}$$

(34)

where $\{n_{max},r_{min},a$ or $r_{max}\}$ and $\{N_{max},R_{min},A$ or $R_{max}\}$ are gaussian basis parameters.

Table 1 Configurations of the $I(J^P)$=$\frac{1}{2}(0^-)$ $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system together with the number of Gaussian basis used. Here, $B=\Xi _{cc}$, $\phi ={\bar{K}}$ and $S_{BB}$ the spin of $\Xi _{cc}\Xi _{cc}$ subsystem. Note that channel 1 and channel 2 are identical

Since the $\Xi _{cc}$ is a doubly charmed $\frac{1}{2}\left( \frac{1}{2}^-\right)$ baryon and ${\bar{K}}$ a $\frac{1}{2}(0^-)$ meson, considering only S-wave interactions and the Fermi-Dirac statistics of the two identical $\Xi _{cc}$ baryons, the quantum numbers of the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system are $I(J^P)=\frac{1}{2}(0^-)$. We found that with 8–15 Gaussian basis functions, the binding energy of the three body system already converges up to a precision of 0.1 MeV. For concreteness, the numerical values reported in this work were obtained with 10 Gaussian basis functions. All the configurations of this three-body system are shown in Table 1.

As the wave function has been constructed, the Schödinger equation of this system is transformed into a generalized matrix eigenvalue problem by the basis expansion:

$$\begin{aligned}{}[T_{\alpha \alpha '}^{ab}+V_{{\alpha \alpha '}}^{ab}-EN_{\alpha \alpha '}^{ab}]\, C_{b,\alpha '} = 0 . \end{aligned}$$

(35)

Here, $T_{\alpha \alpha '}^{ab}$ is the kinetic matrix element, $V_{\alpha \alpha '}^{ab}$ is the potential matrix element and $N_{\alpha \alpha '}^{ab}$ is the normalization matrix element. The eigenenergy E and coefficients are determined by the Rayleigh–Ritz variational principle via the gaussian basis parameters.

4 Thomas collapse in the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system

A problem with the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system is that it is Efimov-like. Thus it will be possible for it to show Thomas collapse [80]. In principle this means that the predictions we will make will be cutoff dependent, as the only way to stabilize the energy of the ground state is to include a short-range repulsive three-body force.

Actually to show the existence of the Thomas collapse in this system we will use the Efimov effect as a proxy. The Efimov effect refers to the appearance of a geometric spectrum in the three-body system when a few of the interacting particles are in the unitary limit, i.e. their scattering lengths diverge. This is complementary to the Thomas collapse: reducing the range of the interaction is equivalent to a relative increase of the scattering length when expressed in units of the range. The presence of the Efimov effect can be deduced from the Faddeev equations for a contact-range potential, which we will not derive in detail here but can be consulted in Refs. [81,82,83]. Instead we will simply use the results derived in other works: if we consider a three-body system of the type AAB, where A and B are two different species of particles and the AB interaction is resonant, the condition for having the Efimov effect is

$$\begin{aligned} \lambda _{\alpha } = \frac{\sin {2 \alpha }}{2 \alpha } \le \lambda , \end{aligned}$$

(36)

with $\lambda$ a geometric factor depending on the characteristics of the AB interaction and quantum numbers of the system, and $\alpha$ an angle given by

$$\begin{aligned} \alpha = \mathrm{arcsin}\,\left( \frac{1}{1 + \frac{m_B}{m_A}} \right) . \end{aligned}$$

(37)

For the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system we have that $m_A = m(\Xi _{cc})$ and $m_B = m(K)$, which gives $\lambda _{\alpha } \simeq 0.389$. The factor $\lambda$ is given in this case by the condition that the $\Xi _{cc} {\bar{K}}$ interaction is strong in the isospin $I = 0$ channel, and can be calculated from the matrix element of the isospin wave functions from the two different permutations of the doubly charmed baryons:

$$\begin{aligned} \lambda = \left\langle H^{c=1}_{\frac{1}{2},0} | H^{c=2}_{\frac{1}{2},0} \right\rangle = \frac{1}{2} . \end{aligned}$$

(38)

From this we have that $\lambda \ge \lambda _{\alpha }$: the conclusion is that for the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system the Efimov effect can indeed happen. But of course, owing to the fact that the $\Xi _{cc} {\bar{K}}$ is far from the unitary limit (i.e. they do not form a shallow bound state), what we expect instead is Thomas collapse. For comparison purposes, in the DDK and $N N {\bar{K}}$ systems we have $\lambda _{\alpha } \simeq 0.531$ and 0.693, respectively, from which we deduce that there is no Thomas collapse in these two cases.

5 Predictions

Once we have determined the required two-body inputs, the calculation of prospective $\Xi _{cc}\Xi _{cc}{\bar{K}}$ ($\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$) trimers is straightforward. For this we will use the GEM, which we have already explained in Sect. 3. As already discussed, the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ three-body system suffers from Thomas collapse, i.e. if the range of the involved two-body $\Xi _{cc} {\bar{K}}$ interaction would be reduced to zero, the three-body system would collapse. Of course in the real world this does not happen because the range of the $\Xi _{cc} {\bar{K}}$ interaction is finite, but this collapse will manifest itself as a strong dependence on the cutoff $R_c$ we have chosen to regularize the potential. Finally, we notice that the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system is completely analogous to the $NN {\bar{K}}$ one: the doubly-charmed baryons and the nucleons belong to the same irreducible representation of the spin and isospin and are therefore interchangeable modulo two differences, one being the masses and the other being the strength of the WT term with the antikaon. For this reason we will also present calculations of the $NN{\bar{K}}$ trimer.

5.1 The $\frac{1}{2}(0^-)$ $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system

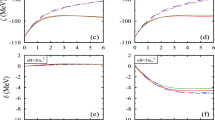
We now present here the $\Xi _{cc} {\bar{K}}$ dimer and $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer predictions. We begin with the dimer, as it is the basic building block for the calculation of the trimer binding energy. As already explained the $\Xi _{cc} {\bar{K}}$ interaction is given by a contact-range potential the strength of which can be related to that of the DK interaction by means of HADS. For the form of the potential we use Eq. (6), where we let the cutoff float in the $R_c =$ 0.5–2.0$\,\mathrm{fm}$ window but set $R_s = 0.1\,\mathrm{fm}$ for the second cutoff we use to model short-range repulsion. We determine the coupling $C(R_c)$ from the condition of reproducing the $D_{s0}^*(2317)$ as a DK bound state with a binding energy of $45\,\mathrm{MeV}$, where the resulting potential is shown in Fig. 2. From this potential and HADS, we predict the $\Xi _{cc} {\bar{K}}$ dimer to have a binding energy of 49–64$\,\mathrm{MeV}$ in the absence of a repulsive core, and 49–63 MeV if there is a repulsive core with $C_S = 1000\,\mathrm{MeV}$, from which we deduce that the influence of a repulsive core is negligible. A more detailed compilation of the binding energies of the dimer for different cutoffs can be found in Table 2.⁴ We note that the binding energy of the $\Xi _{cc}{\bar{K}}$ bound state is larger than that of the DK bound state because the $\Xi _{cc}$ baryon is heavier than the D meson.

Fig. 2

Weinberg–Tomozawa $\Xi _{cc}{\bar{K}}$ potential with specified $R_s$, $C_S$, and $R_c$. The other parameter $C(R_c)$ is determined by reproducing the $D_{s0}^*(2317)$

Table 2 Parameters ($C_S$, $C(R_c)$ in MeV, and $R_s$, $R_c$ in fm), binding energies ($B_2$, $B_3$ in MeV) and root mean square radii ($r_2$, $r_3$ in fm) of the $\Xi _{cc}{\bar{K}}$ and $\Xi _{cc}\Xi _{cc}{\bar{K}}$ bound states. Note that $r_3(\Xi _{cc}{\bar{K}})$ and $r_3(\Xi _{cc}\Xi _{cc})$ are the RMS radii of the corresponding two-body subsystems of the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer. The uncertainties are generated by considering a $25\%$ breaking in HADS

Now for the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system, besides the $\Xi _{cc}{\bar{K}}$ interaction explained in the previous paragraph, we also need the $\Xi _{cc}\Xi _{cc}$ potential. For this we use the OBE potential described in Eqs. (15–19). With this we arrive at the results we show in Table 2.

A few comments are in order at this point. First, the 3-body binding energy of the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system increases as the cutoff $R_c$ decreases. The origin of this cutoff dependence lies in the fact that the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system is susceptible to Thomas collapse, i.e. if we were to reduce the cutoff $R_c$ to zero, the binding energy of the system will diverge: $B_3 \rightarrow \infty$. For the cutoff range we have chosen, i.e. $R_c =$ 0.5–2.0$\,\mathrm{fm}$, the binding energy of the trimer varies between 80–118 MeV. Indeed it can be appreciated that the possibility of Thomas collapse in the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system translates into a considerable cutoff dependence of the results, yet the conclusion that the system binds is solid, as it happens even for really soft cutoffs like $R_c = 2.0\,\mathrm{fm}$. Second, if $R_c$ is large enough (1.5–2.0$\,\mathrm{fm}$), a second bound state appears. This additional bound state is expected to be a cutoff artifact: the cutoffs for which it appears are relatively soft, definitely larger than the size of the hadrons we are considering here. Be it as it may, the bottom-line is that the existence of the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ bound state is rather robust.

The uncertainties of our predictions as listed in Table 2 come from two different sources. One is violation of HADS, which is not a perfectly preserved symmetry, but instead it is expected to be broken at the $25\%$ level. This will affect the two two-body potentials on which the calculation of the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ trimer relies: the $\Xi _{cc}{\bar{K}}$ and the $\Xi _{cc}\Xi _{cc}$ potentials. In both cases we are inferring the strength of the potential from HADS and the corresponding potential for the DK and DD systems, which means that the mentioned $25\%$ relative uncertainty applies. In addition the individual couplings of the $\Xi _{cc}\Xi _{cc}$ potential inherit the same type of uncertainties as in the DD potential, as discussed in Ref. [75]. The origin of these uncertainties lies in the problem of determining the value of the different coupling constants in the OBE model, where we simply assume them to compound into a single uncertainty of about $30\%$ in the value of the OBE potential, These two sources of uncertainty – HADS and the OBE couplings – are then summed in quadrature (as we expect them to be independent error sources)

$$\begin{aligned} \mathrm{Error}=\sqrt{{\mathrm{Error}}(\mathrm{WT})^2+\mathrm{Error}(\mathrm{OBE})^2} \end{aligned}$$

(39)

where $\mathrm{Error}(\mathrm{WT})$ is calculated by scaling the $\Xi _{cc}{\bar{K}}$ potential by a factor of 0.75–1.25, while keeping the OBE $\Xi _{cc}\Xi _{cc}$ potential unchanged. Similarly, $\mathrm{Error}(\mathrm{OBE})$ is calculated by scaling the OBE $\Xi _{cc}\Xi _{cc}$ potential with a factor of 0.7–1.3, while keeping the $\Xi _{cc}{\bar{K}}$ potential unchanged. We find that the influence on the binding energy form the $\mathrm{Error}(\mathrm{WT})$ is about a few tens of MeV and that from $\mathrm{Error}(\mathrm{OBE})$ is less than 1 MeV. Therefore, we conclude that the dominant uncertainty in the binding energy of the trimer is from that of the $\Xi _{cc}{\bar{K}}$ interaction.

It is instructive to show how the presence of a third particle in a three-body system affects the size of the two-body subsystems. For this we calculate the root mean square (RMS) radius of the $\Xi _{cc}{\bar{K}}$ pair in the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer and compare it with that of the $\Xi _{cc}{\bar{K}}$ dimer. Table 2 shows that with the cutoff $R_c$ ranging from 0.5–2.0 fm, the distance between $\Xi _{cc}$ and ${\bar{K}}$ is slightly smaller in the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer than that of the $\Xi _{cc}{\bar{K}}$ dimer, which indicates that the second $\Xi _{cc}$ makes the $\Xi _{cc}{\bar{K}}$ subsystem a bit more bound. If we turn our attention to the $\Xi _{cc}\Xi _{cc}$ subsystem, for a cutoff $\Lambda =1.01$ GeV, the K meson pulls them together to the point that their RMS radius is slightly smaller than that of the $\Xi _{cc}{\bar{K}}$ pair, see Table 2. The same happens in the $NN{\bar{K}}$ and DDK systems [9], which indicates that the K meson plays an important role in forming some three-body bound states.

5.2 The $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system

Now, to study the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system, we can apply the same formalism as we did before for the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ case. For the description of the $\Xi _{cc}\bar{\Xi }_{cc}$ potential we use the OBE potential as presented in Sect. 2.2, where the only difference with the $\Xi _{cc}\Xi _{cc}$ case is a change of the pion- and omega- exchange contributions. For $\Xi _{cc}K$, we can simply relate it to the $D{\bar{K}}$ interacton via HADS. From chiral symmetry, it is well-known that the LO $D{\bar{K}}$ potential in the isoscalar channel is half the strength of the DK one, see for instance Ref. [14]. Therefore the $\Xi _{cc}K$ interaction will also be half the $\Xi _{cc}{\bar{K}}$ one mentioned in Sect. 2.1, see Eqs. (1–5).

First, we discuss the $\Xi _{cc}\bar{\Xi }_{cc}$ system. Since both the $\Xi _{cc}$ and the $\bar{\Xi }_{cc}$ have spin 1/2 and isospin 1/2 but have opposite parity, the allowed quantum numbers of the $\Xi _{cc}\bar{\Xi }_{cc}$ two-body system with S-wave interactions are $I(J^P)=0(0^-)$, $0(1^-)$, $1(0^-)$ and $1(1^-)$. The isospin wave functions read as

$$\begin{aligned} \left| \Xi _{cc}\bar{\Xi }_{cc}(I=0,I_3=0)\right\rangle= & {} \frac{1}{\sqrt{2}}\left( \left| \Xi _{cc}^+\Xi _{cc}^-\right\rangle + \left| \Xi _{cc}^{++}\Xi _{cc}^{--}\right) \right\rangle ,\nonumber \\ \left| \Xi _{cc}\bar{\Xi }_{cc}(I=1,I_3=0)\right\rangle= & {} \frac{1}{\sqrt{2}}\left( \left| \Xi _{cc}^+\Xi _{cc}^-\right\rangle - \left| \Xi _{cc}^{++}\Xi _{cc}^{--}\right\rangle \right) ,\nonumber \\ \left| \Xi _{cc}\bar{\Xi }_{cc}(I=1,I_3=+1)\right\rangle= & {} \left| \Xi _{cc}^{++}\Xi _{cc}^-\right\rangle ,\nonumber \\ \left| \Xi _{cc}\bar{\Xi }_{cc}(I=1,I_3=-1)\right\rangle= & {} -\left| \Xi _{cc}^+\Xi _{cc}^{--}\right\rangle , \end{aligned}$$

(40)

for which the corresponding Coulomb potentials are

$$\begin{aligned} V_{\Xi _{cc}\bar{\Xi }_{cc}}^C(r;I=0,I_3=0)&=-\frac{5\alpha }{2r},\nonumber \\ V_{\Xi _{cc}\bar{\Xi }_{cc}}^C(r;I=1,I_3=0)&=-\frac{5\alpha }{2r},\nonumber \\ V_{\Xi _{cc}\bar{\Xi }_{cc}}^C(r;I=1,I_3=+1)&=-\frac{2\alpha }{r},\nonumber \\ V_{\Xi _{cc}\bar{\Xi }_{cc}}^C(r;I=1,I_3=-1)&=-\frac{2\alpha }{r}. \end{aligned}$$

(41)

Table 3 $\Xi _{cc}\bar{\Xi }_{cc}$ binding energies (in units of MeV) with OBE and Coulomb potentials. The cutoff $\Lambda$ of the OBE potential is chosen to be 1.01GeV

We show the results for the $\Xi _{cc}\bar{\Xi }_{cc}$ system in Table 3. With the OBE potential only, the isospin 0 state binds while the isospin 1 state does not. This is because the OBE potential is more attractive in the isospin 0 channel. However, because $\Xi _{cc}$ and $\bar{\Xi }_{cc}$ have opposite electric charge, the Coulomb interaction is significant in this two-body system, to such an extent that it alone can bind the two-body systems, while with OBE only, some of the states are not bound. What is more interesting is that there is always a very loosely-bound excited state. One should also note that in the $I_3=0$ channel the positive and negative charged particles can annihilate each other, but we will ignore this effect in this manuscript.

Table 4 Binding energies (in units of MeV) and RMS radii (in units of fm) of $0\left( \frac{1}{2}^-\right)$ $\Xi _{cc}K$ and $\frac{1}{2}(0^+)$, $\frac{1}{2}(1^+)$ $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ bound states. $R_c$ in fm is the cutoff of $\Xi _{cc}{\bar{K}}$ and $\Xi _{cc}K$ potentials

Since the $\Xi _{cc}$($\bar{\Xi }_{cc}$) is a doubly charmed $\frac{1}{2}^+$ $\left( \frac{1}{2}^-\right)$ baryon (antibaryon) and ${\bar{K}}$ a spin 0 meson, considering only S-wave interactions, the spin of the possible $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ trimer can be 0 or 1. We note that in the isospin 1 channel the $\Xi _{cc} K$ interaction is repulsive while the $\Xi _{cc} {\bar{K}}$ vanishes, from which we deduce that the preferred quantum numbers of the possible $\Xi _{cc} \bar{\Xi }_{cc} K$ trimers will most likely be $\frac{1}{2}(0^+)$ and $\frac{1}{2}(1^+)$. In the numerical calculation, the number of Gaussian basis functions is taken to be the same as in the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system. For the $\Xi _{cc}K$ two-body system, we included the repulsive Coulomb interaction. For the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system, because there are both positive and negative charged particles, the contributions of the Coulomb interaction cancels out. Therefore, the Coulomb interaction was neglected.

Although the $\Xi _{cc}K$ interaction is only half the strength of the $\Xi _{cc}{\bar{K}}$ interaction, indeed this hidden-charmed three-body system is likely to bind. In Table 4, we show the results for the binding energies and RMS radii of the $0\left( \frac{1}{2}^-\right)$ $\Xi _{cc}K$ and $\frac{1}{2}(0^+)$, $\frac{1}{2}(1^+)$ $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ bound states. The $\Xi _{cc}K$ system is bound with $R_c=$ 1–2 fm, while not with $R_c=0.5$ fm. Considering that $R_c$ represents the effective interaction range, it seems that the $\Xi _{cc}K$ is more likely to bind if the interaction range is large. For the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system, both the $\frac{1}{2}(0^+)$ state and the $\frac{1}{2}(1^+)$ state are bound, with binding energies of about 56–68 MeV and a splitting about 1 MeV, while the former is slightly more bound. Compared with the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system, the binding energy is smaller, thus the sizes of the subsystems are a bit larger.

5.3 The $NN{\bar{K}}$ system as an analogue of the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system

As previously mentioned, the charmed meson D and doubly charmed baryon $\Xi _{cc}$ can be seen as an analogue to the nucleon: while the heavy quarks act as spectators, the light-quark within these heavy hadrons belong to the same spin and isospin irreducible representations as the nucleon (see, e.g.,  [77]). Thus it is natural to see the DDK and $\Xi _{cc}\Xi _{cc}{\bar{K}}$ systems as heavy counterparts of the $N N {\bar{K}}$ system.

Furthermore, the origin of the same $N{\bar{K}}$ interaction is the WT term which is also responsible for the binding of the DK and $\Xi _{cc} {\bar{K}}$ systems. Here there is a difference though: the nucleon belongs to the 8 representation of the SU(3)-flavor group, while the D and $\Xi _{cc}$ heavy hadrons to the $\bar{3}$ and 3 ones. This means that the strength of the WT term is not the same for $N {\bar{K}}$ as it is for DK and $\Xi _{cc} {\bar{K}}$ (in fact, for $N{\bar{K}}$ it is more attractive). Using the WT term or the chiral potential as kernel to the Lippmann–Schwinger or Bethe–Salpeter equations, one can describe the $\Lambda (1405)$ as a ${\bar{K}}N$ bound state [84,85,86,87,88,89,90,91]. In addition, the $NN{\bar{K}}$ system has been studied rather extensively and it seems that all the approaches lead to the conclusion that it should bind [26,27,28,29,30,31,32,33,34,35,36,37,38, 40,41,42], while only differing in minor details. If this were not enough, all the experiments performed so far support the existence of such a state [43,44,45, 47,48,49], again only differing in minor details.

Following the logic with which we studied the $\Xi _{cc}\Xi _{cc}{\bar{K}}$ system, here we calculate the binding energy of the $NN{\bar{K}}$ bound state using the $N{\bar{K}}$ and NN potentials as input. For fixing the strength of the $N{\bar{K}}$ interaction we simply reproduce the location of the $\Lambda (1405)$ with the potential of Eq. (6). For the NN interaction we use the OBE model. The binding energy of the $NN{\bar{K}}$ trimer is listed in Table 5 for different cutoffs. In the same table we also show the values of the coupling that reproduces the $\Lambda (1405)$ pole as a $N{\bar{K}}$ bound state with a binding energy $B_2 = 29.4\,\mathrm{MeV}$. The binding energy of the $NN{\bar{K}}$ trimer ranges from 35–$43\,\mathrm{MeV}$, where the cutoff dependence is relatively weak in comparison to the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system. The reason is that the $NN{\bar{K}}$ does not suffer from Thomas collapse as a consequence that the mass ratio between the nucleon and the kaon is not large enough as to trigger this effect. We notice that the inclusion of the $NN{\bar{K}}$ system in the present manuscript should be viewed mostly as a consistency check of the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ calculation: there is a large literature of calculations of the $NN{\bar{K}}$ system that are far more sophisticated that the one presented here.

Table 5 Parameters ($C_S$, $C(R_c)$ in MeV, and $R_s$, $R_c$ in fm) of the $N{\bar{K}}$ potential and binding energies ($B_2$ and $B_3$ in MeV) of the $N{\bar{K}}$ and $I(J^P)$=$\frac{1}{2}(0^-)$ $NN{\bar{K}}$ bound states. The parameters are determined by reproducing the $\Lambda (1405)$ with a binding energy 29.4 MeV with respect to the $N{\bar{K}}$ threshold

6 Summary

In this work we have investigated the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system. We have reached the conclusion that it is likely to bind. This is mostly a consequence of HADS, a type of heavy-quark symmetry that relates the $\Xi _{cc} {\bar{K}}$ interaction to the DK one. From this symmetry and the fact that previous theoretical explorations point out to the possibility of bound DDK [7, 8] and DDDK clusters [9], the natural expectation is that the $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system binds too. Concrete calculations within the GEM framework indicate that (i) the two-body $\Xi _{cc}{\bar{K}}$ system has a binding energy $B_2 = 49-64\,\mathrm{MeV}$ (ii) while for the three-body $\Xi _{cc} \Xi _{cc} {\bar{K}}$ system the binding energy is $B_3 =$ 80–118$\,\mathrm{MeV}$.

In the case of the two-body calculation, from HADS we expect the $\Xi _{cc} {\bar{K}}$ potential to be identical to the DK one, where for the later case the strength of the potential can be completely determined from the hypothesis that the $D_{s0}^*(2317)$ is a DK bound state. At the level of approximation we are considering, this interaction is given by the WT term, though we additionally considered the possibility of a short-range repulsive core in the $\Xi _{cc} {\bar{K}}$ potential to mimic the effect of subleading corrections. The uncertainty in the two-body binding energy comes mostly from violations of HADS, which we take to be as large as 25% percent.

For the three-body $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer the uncertainties are definitely larger because besides HADS we also have a sizable cutoff dependence: this trimer is in principle susceptible to Thomas collapse, i.e. if the range of the $\Xi _{cc} {\bar{K}}$ interaction were to be taken to zero the trimer binding energy would diverge, hence the cutoff dependence. This problem can be effectively circumvented by the fact that the size of the $\Xi _{cc}$ or $\bar{K}$ hadrons is finite or, more elegantly, by the inclusion of a repulsive short-range three-body force that will stabilize the results. Here we opt for the finite-cutoff solution, owing to its simplicity but also to the fact that the strength of a prospective three-body force should be determined from the data. Be it as it may, we consider the existence of a relatively compact $\Xi _{cc}\Xi _{cc}{\bar{K}}$ trimer as a robust conclusion. Besides, we can deduce the existence of additional trimers from the other heavy-quark symmetries. For instance, from heavy-flavor symmetry there should be $\Xi _{bc} \Xi _{bc} {\bar{K}}$ and $\Xi _{bb} \Xi _{bb} {\bar{K}}$ trimers.

With the same formalism, we have also studied the $\Xi _{cc}\bar{\Xi }_{cc}{\bar{K}}$ system and found that it is likely to bind as well, yielding a $\frac{1}{2}(0^+)$ state with a binding energy about 56–68 MeV and a $\frac{1}{2}(1^+)$ state with a binding energy about 56–67 MeV. Considering the hidden charm nature of these states, they are easier to be found experimentally.

Finally we applied our framework to study the $N{\bar{K}}$ and $NN{\bar{K}}$ systems. The motivation is a very simple analogy between the charmed mesons D, the doubly charmed baryons $\Xi _{cc}$ and the nucleon N, the three of which belong to the same representation of light-quark spin and isospin. From this analogy the only differences between few nucleons and few doubly-charmed baryons systems are the specific details of the potential, i.e. the coupling constants and masses. If we determine the $N{\bar{K}}$ interaction from the condition that the $\Lambda (1405)$ is a $N {\bar{K}}$ bound state, we reach the conclusion that the binding energy of the $NN{\bar{K}}$ system is $B_3 =$ 35–43$\,\mathrm{MeV}$ with respect to the three-body mass threshold, which is consistent with previous studies and experiments.