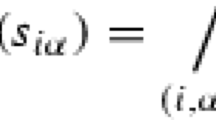1 Introduction

Understanding of the structure of spacetime at very small scales is one of the most challenging problems in theoretical physics: more so as it is, as we commonly believe, related to the properties of gravity at small scales, that is to quantization of gravity. In the absence of a sufficient amount of experimental data, it is presently approached by mathematical methods: still there are basic tests which every model of quantum spacetime has to satisfy, as the mathematical consistency and the existence of a classical limit, usually to general relativity.

A feature very often discussed in relation to quantization is discreteness of spacetime. Discreteness can mathematically be implemented in various ways, for example by endowing spacetime with lattice or simplicial structure. When discreteness is introduced by means of representation of the position vector by noncommuting operators or matrices we speak of fuzzy spaces. Assumption that coordinates are operators comes from quantum mechanics: in fact, it is quite natural (perhaps even too elementary) to presume that generalization of \(\,[x^\mu ,x^\nu ] =0\,\) to \(\,[x^\mu ,x^\nu ] \ne 0\,\) describes the shift of physical description to lower length scales. Operator representation has a potential to solve various problems of classical gravity and quantum field theory: it introduces minimal length, which in the dual, momentum space, can in principle resolve the problem of UV divergences; singular configurations of gravitational field can potentially be dismissed as corresponding to non-normalizable states, and so on. In addition, algebraic representation allows for a straightforward description of spacetime symmetries. Perhaps the main drawback of the assumption of discreteness is a loss of geometric intuition which is in many ways inbuilt in our understanding of gravity.

There are various ways to generalize geometry: one of the most important parts of any generalization is the definition of smoothness. In noncommutative geometry, derivatives are usually given by commutators; once they are defined, one can proceed more or less straightforwardly to differential geometry. We shall in the following use a variant of noncommutative differential geometry which was introduced by Madore, known as the noncommutative frame formalism [1]. It is a noncommutative generalization of the Cartan moving frame formalism and gives a very natural way to describe gravity on curved noncommutative spacetimes. In particular classical, that is commutative, limit of such noncommutative geometry is usually straightforward.

Let us introduce the notation. Noncommutative space is an algebra \(\mathcal {A}\) generated by coordinates \(x^\mu \) which are hermitian operators; fields are functions \(\phi (x^\mu )\) on \(\mathcal {A}\). Derivations or vector fields are represented by commutators. A special set of derivations \(e_\alpha \) can be chosen to define the moving frame,

$$\begin{aligned} e_\alpha \phi =[p_\alpha , \phi ], \qquad \phi \in \mathcal {A} \end{aligned}$$
(1)

Derivations \(e_\alpha \) are generated by antihermitian operators, momenta \(p_\alpha \), which can but need not belong to algebra \(\mathcal {A}\). 1-forms \(\theta ^\alpha \) dual to \(e_\alpha \) define the differential,

$$\begin{aligned} \theta ^\alpha (e_\beta ) = \delta ^\alpha _\beta , \qquad d\phi = (e_\alpha \phi )\theta ^\alpha . \end{aligned}$$
(2)

Supplementary condition which allows to interpret \(\theta ^\alpha \) as a locally orthonormal basis is \([\phi ,\theta ^\alpha ]=0\). In addition, one imposes consistency constraints on both structures, algebraic (associativity) and differential (\(d^2=0\)), and compatibility relations between them.

General features of the noncommutative frame formalism and many applications to gravity are known [2,3,4,5]; the aim of our present investigation is to construct four-dimensional noncommutative spacetimes which correspond to known classical configurations of gravitational field. This means, to find algebras and differential structures which are noncommutative versions of, for example, black holes or cosmologies. One very important idea in this context is that spacetimes of high symmetry can be naturally represented within the algebras of the symmetry groups. The first model of such noncommutative geometry was the fuzzy sphere [6, 7]: it has a number of remarkable properties which make it a role example for understanding what fuzzy geometry should or could mean. Different properties of the fuzzy sphere were used as guidelines to define other fuzzy spaces [8,9,10,11], including for us very important noncommutative de Sitter space in two and four dimensions [12,13,14]. In our previous paper [15] we analyzed differential-geometric properties of fuzzy de Sitter space in four dimensions realized within the algebra of the \(\text {SO}(1,4)\) group. We found two different differential structures with the de Sitter metric as commutative limit. Here we analyze geometry of fuzzy de Sitter space that is the spectra of the embedding coordinates.

The plan of the paper is the following. In Sect. 2 we introduce notation for the \(\text {SO}(1,4)\), review some results of [15] and discuss the flat limit of fuzzy de Sitter space revealing its relation to the Snyder space. In Sect. 3 we solve the eigenvalue problem of coordinates in the unitary irreducible representation \((\rho , s=\frac{1}{2})\,\) of the principal continuous series. The obtained spectrum we compare to the known group-theoretic result in Sect. 4.

2 Metric and scaling limits

We start with the algebra of the de Sitter group \(\text {SO}(1,4)\) with generators \(M_{\alpha \beta }\), (\(\alpha , \beta = 0,1,2,3,4\)) and signature \(\,\eta _{\alpha \beta } = \mathrm{diag}(+----)\),Footnote 1

$$\begin{aligned}{}[M_{\alpha \beta }, M_{\gamma \delta }]= & {} - i(\eta _{\alpha \gamma } M_{\beta \delta } -\eta _{\alpha \delta } M_{\beta \gamma } \nonumber \\&-\eta _{\beta \gamma } M_{\alpha \delta }+ \eta _{\beta \delta } M_{\alpha \gamma }). \end{aligned}$$
(3)

The only W-symbol of the \(\text {SO}(1,4)\) group, [16], is the vector \(W^\alpha \) which is quadratic in the generators

$$\begin{aligned}&W^\alpha =\dfrac{1}{8} \,\epsilon ^{\alpha \beta \gamma \delta \eta } M_{\beta \gamma } M_{\delta \eta }, \end{aligned}$$
(4)
$$\begin{aligned}&[M_{\alpha \beta }, W_\gamma ] = - i(\eta _{\alpha \gamma }W_\beta -\eta _{\beta \gamma }W_\alpha ). \qquad \end{aligned}$$
(5)

The Casimir operators of the \(\text {SO}(1,4)\) are

$$\begin{aligned} {{\mathcal {Q}}} = -\frac{1}{2} \, M_{\alpha \beta } M^{\alpha \beta }, \qquad \ {{\mathcal {W}}} =- W_\alpha W^\alpha . \end{aligned}$$
(6)

The de Sitter algebra can be contracted to the Poincaré algebra by the Inönü–Wigner contraction

$$\begin{aligned} M_{\alpha 4} \rightarrow \mu M_{\alpha 4}, \qquad M_{\alpha \beta }\rightarrow M_{\alpha \beta }, \qquad \mathrm{for}\ \ \mu \rightarrow \infty . \end{aligned}$$
(7)

In the contraction limit \(M_{\alpha 4}\) become the generators of 4-translations while \(M_{ij}\) and \(M_{0i}\) generate 3-rotations and boosts. Further, \(W_\alpha \rightarrow \mu W_\alpha \,\), \(W_4\rightarrow W_4\,\) become the components of the Pauli–Lubanski vector of the Poincaré group (one can assume that \(W_4\rightarrow 0\)). In the contraction limit \(\,{{\mathcal {Q}}}\,\) and \(\,{{\mathcal {W}}}\,\) become the Casimir operators of the Poincaré group, \({{\mathcal {Q}}}\rightarrow \mu ^2m^2\), \({{\mathcal {W}}}\rightarrow \mu ^2 W^2\). Relations between the de Sitter and the Poincaré algebras exist also at the level of representations but not in general, only in some particular cases.

It is obvious that there is a strong analogy between commutative four-dimensional de Sitter space described as an embedding in five flat dimensions,

$$\begin{aligned} \eta _{\alpha \beta } \mathtt{x}^\alpha \mathtt{x}^\beta =-\, \frac{3}{\varLambda }=\mathrm{const}, \end{aligned}$$
(8)

and the Casimir relation

$$\begin{aligned} \eta _{\alpha \beta }W^\alpha W^\beta = -\mathcal {W} =\mathrm{const}. \end{aligned}$$
(9)

It is therefore natural identify \(W^\alpha \) with the embedding coordinates, as first proposed in [12],

$$\begin{aligned} x^\alpha = \ell \, W^\alpha \end{aligned}$$
(10)

and to define fuzzy de Sitter space as a unitary irreducible representation (UIR) of the \(\text {so}(1,4)\) algebra. This definition makes senseFootnote 2 in all cases except when \(\mathcal {W}=0\), that is, for Class-I irreducible representations.

Group generators are dimensionless so a constant \(\,\ell \) is introduced in (10) to give \(x^\alpha \) a dimension of length.Footnote 3 There are two scales in our problem: the cosmological constant, \(\varLambda \sim (10^{26}\mathrm{m})^{-2}\), and the Planck length, \(\ell _{Pl}\sim 10^{-35} \mathrm{m}\). In preference to \( \ell _{Pl} \) we will use third constant, noncommutativity parameter , and assume that

(11)

The upper bound in (11) is a rough experimental limit to . Assumption which is often taken, , would indicate that noncommutative geometry is directly related to quantization of gravity; a more moderate (11) means that noncommutative geometry is or might be an effective description of quantized gravity in the appropriate range of distances. We thus scale coordinates as

(12)

Then the relation between the quartic Casimir operator and the cosmological constant reads

(13)

Relations as (12) define the quantization condition. Dimensionally, we could have assumed more general relation of the form

(14)

but we chose the simplest, \(n=0\). For an interesting discussion of the quantization condition defined with respect to the Compton wavelength of the elementary system, see [13].

Limit is the commutative limit of fuzzy de Sitter space. From

$$\begin{aligned}{}[W^\alpha , W^\beta ] = -\frac{i}{2}\, \epsilon ^{\alpha \beta \gamma \delta \eta }\, W_\gamma M_{\delta \eta } \end{aligned}$$
(15)

we see that position commutator is proportional to ,

(16)

that is, for coordinates commute. The flat (noncommutative) limit on the other hand can be obtained when we consider de Sitter space in a ‘small neighbourhood’ of a specific point, for example at the north pole,

$$\begin{aligned} x^4 \approx \sqrt{\frac{3}{\varLambda }}, \qquad x^\alpha \approx 0, \qquad \alpha = 0,1,2,3 \end{aligned}$$
(17)

for \( \varLambda \rightarrow 0\). At the level of the symmetry group this limit is defined by the Inönü–Wigner contraction (7). Commutation relations contract to

$$\begin{aligned}{}[x^4,x^\alpha ] =-\frac{i}{2}\,\sqrt{\frac{\varLambda }{3}}\,\, \epsilon ^{4\beta \gamma \delta \eta }\, x_\gamma M_{\delta \eta } \rightarrow 0,\qquad \varLambda \rightarrow 0, \end{aligned}$$
(18)

and it is consistent to take \(\, x^4 =\sqrt{\frac{3}{\varLambda }}\,\)= const. Furthermore,

(19)
(20)

Denoting , we see that we obtained the dual to the Snyder algebra. Namely, we found

$$\begin{aligned}{}[x^i,x^j]\sim ia^2 \epsilon ^{ijk} M_{0k},\qquad [x^0,x^i]\sim ia^2 \epsilon ^{ijk} M_{jk}, \end{aligned}$$
(21)

whereas the position algebra of [17] reads

$$\begin{aligned}{}[x^i,x^j]\sim ia^2 M^{ij},\qquad [x^0,x^i]\sim ia^2 M^{0i}. \end{aligned}$$
(22)

The limit \(\mu \rightarrow \infty \) corresponds to \(a\rightarrow 0\).

In [15], two sets of momenta that define fuzzy geometries with correct commutative limits to classical de Sitter space were proposed. In the noncommutative frame formalism, fulfil stricter requirements than coordinates: first, they close into an algebra which is at most quadratic. In addition, if we wish to interpret tetrad \(e^\alpha _A \) and metric \( \, g^{\alpha \beta } = \eta ^{AB} e^\alpha _A \, e^\beta _B \, \) as fields, we have to require that the frame elements depend only on coordinates,

$$\begin{aligned}{}[p_A, x^\alpha ] =e^\alpha _A(x), \qquad \ \ x\in {{\mathcal {A}}}. \end{aligned}$$
(23)

It is simplest to choose \(p_A\) among the group generators.Footnote 4 When momenta close into a Lie algebra, \(\, [p_A, p_B] = C^D{}_{AB}\, p_D\, \), the curvature defined in the framework of the noncommutative frame formalism is constant [1], and the curvature scalar is given by

$$\begin{aligned} R = \frac{1}{4}\, C^{ABD} C_{DAB}. \end{aligned}$$
(24)

This means in particular that, in our case, momenta scale as \( \sqrt{ \varLambda }\, \).

If we wish to preserve the full de Sitter symmetry on fuzzy de Sitter space, we choose as momenta all ten generators \(M_{\alpha \beta }\),

$$\begin{aligned} i p_A = \sqrt{ \zeta \varLambda }\, M_{\alpha \beta }, \end{aligned}$$
(25)

where index \(A=1,\dots , 10 \), denotes antisymmetric pairs \([\alpha \beta ]\). Normalization of the scalar curvature to \(\, R=4\varLambda \,\) gives \(\,\zeta = 1/3\). There are ten frame 1-forms \(\theta ^A\). Assuming the flat frame, \(g^{AB}=\eta ^{AB}\), with signature \(\, (++++++----)\), for the spacetime components of the metric, \(\, g^{\alpha \beta } = e^\alpha _A e^\beta _B \eta ^{AB} \ (\alpha = 0,1,2,3,4) \), we obtain

$$\begin{aligned} g^{\alpha \beta } = \eta ^{\alpha \beta } - \frac{ \varLambda }{3}\, x^\beta x^\alpha . \end{aligned}$$
(26)

In the commutative limit \(\,g^{\alpha \beta }\) is singular and reduces to the projector to the four-dimensional de Sitter space.

The second choice of momenta is

$$\begin{aligned}&i{\tilde{p}}_0 =\sqrt{\tilde{\zeta }\varLambda } \, M_{04},\quad \nonumber \\&i{\tilde{p}}_i =\sqrt{\tilde{\zeta }\varLambda } \,(M_{i4}+M_{0i}), \quad i=1,2,3. \end{aligned}$$
(27)

There are now four frame 1-forms \(\,\tilde{\theta }^\alpha \), \(\alpha = 0,1,2,3\). Calculating the spacetime components of the metric, for the noncommutative equivalent of the line element we find

$$\begin{aligned} {\tilde{d}}s^2 = (\tilde{\theta }^0)^2- (\tilde{\theta }^i)^2 = \tilde{d}\tau ^2 -e^{\frac{2\tau }{l}} (d\tilde{x}^i)^2 \end{aligned}$$
(28)

with natural identification of the cosmological time \(\tau \),

$$\begin{aligned} \frac{\tau }{\ell }= -\log \left( \frac{x^0+x^4}{\ell } \right) . \end{aligned}$$
(29)

This noncommutative metric and the corresponding moving frame do not possess the complete de Sitter symmetry. Normalization of the scalar curvature to the usual value gives \(\,\tilde{\zeta }= 16/3\).

3 Coordinates

Let us consider the spectra of the embedding coordinates \(x^\alpha \). Classification of the unitary irreducible representations of the de Sitter group was done in [18,19,20]; the UIR’s of the \(\text {SO}(1,4)\) are induced from representations of its maximal compact subgroup \(\text {SO}(4)\). The representation basis \(\,\{ f^{k,k'}_{m,m'}\} \) is discrete (k and \(k^\prime \) label the UIR’s of the two \(\text {SO}(3)\) subgroups of \(\text {SO}(4)\)). The unitary irreducible of the \(\text {SO}(1,4)\) are infinite-dimensional, labelled by two quantum numbers, \(\rho \) (or \(\nu =i\rho \), \(q=1/2+i\rho \)) and s.Footnote 5 They are grouped in three series,

  • principal continuous series, \(\rho \in \mathbf{R}\), \(\rho \ge 0\), \(s = 0, \frac{1}{2}, 1, \frac{3}{2},\dots \)

    \({{\mathcal {Q}}} = -s(s+1)+ \frac{9}{4} + \rho ^2\),   \({{\mathcal {W}}} = s(s+1)( \frac{1}{4} + \rho ^2)\),

  • complementary continuous series, \(\nu \in \mathbf{R}\), \(\vert \nu \vert <\frac{3}{2} \), \(s = 0, 1, 2\dots \)

    \({{\mathcal {Q}}} = -s(s+1)+ \frac{9}{4} - \nu ^2\),   \({{\mathcal {W}}} = s(s+1)( \frac{1}{4} - \nu ^2)\), and

  • discrete series, \(s = \frac{1}{2}, 1, \frac{3}{2},2 \dots \), \(q= s,s-1,\dots 0\ \mathrm{or}\ \frac{1}{2}\) \({{\mathcal {Q}}} = -s(s+1) - (q+1)(q-2)\),   \({{\mathcal {W}}} = - s(s+1)q(q-1)\).

In the discrete case there are two inequivalent representations \(\pi ^\pm _{s,q}\,\) for each value of q and s; values of the Casimir operators are discrete.

Using known matrix elements of \(M_{\alpha \beta }\) from [20], one can calculate matrix elements of \(W^\alpha \) in basis \(\, \{f^{k,k'}_{m,m'} \}\). We find

$$\begin{aligned} {W_0}&f^{k,k'}_{m,m'}=\left( k'(k'+1)-k(k+1)\right) f^{k,k'}_{m,m'}, \end{aligned}$$
(30)
$$\begin{aligned} {W_4}&f^{k,k'}_{m,m'} = -\dfrac{i}{2} A_{k,k'} (k-k') \nonumber \\&\left( \sqrt{(k-m+1)(k'+m'+1)}\, f^{k+\frac{1}{2},k'+\frac{1}{2}}_{m-\frac{1}{2},m'+\frac{1}{2}} \right. \nonumber \\&\left. - \sqrt{(k+m+1)(k'-m'+1)}\, f^{k+\frac{1}{2},k'+\frac{1}{2}}_{m+\frac{1}{2},m'-\frac{1}{2}} \right) \nonumber \\&-\frac{i}{2} B_{k,k'} (k+k'+1) \nonumber \\&\left( \sqrt{(k+m)(k'+m'+1)}\, f^{k-\frac{1}{2},k'+\frac{1}{2}}_{m-\frac{1}{2},m'+\frac{1}{2}}\right. \nonumber \\&\left. + \sqrt{(k-m)(k'-m'+1)}\, f^{k-\frac{1}{2},k' +\frac{1}{2}}_{m+\frac{1}{2},m'-\frac{1}{2}} \right) \nonumber \\&-\frac{i}{2} C_{k,k'} (k+k'+1) \nonumber \\&\left( \sqrt{(k-m+1)(k'-m')}\, f^{k+\frac{1}{2},k'-\frac{1}{2}}_{m-\frac{1}{2},m'+\frac{1}{2}} \right. \nonumber \\&\left. + \sqrt{(k+m+1)(k'+m')}\, f^{k+\frac{1}{2},k'-\frac{1}{2}}_{m+\frac{1}{2},m'-\frac{1}{2}} \right) \nonumber \\&-\frac{i}{2} D_{k,k'} (k-k') \nonumber \\&\left( \sqrt{(k+m)(k'-m')}\, f^{k-\frac{1}{2},k'-\frac{1}{2}}_{m-\frac{1}{2},m'+\frac{1}{2}} \right. \nonumber \\&\left. - \sqrt{(k-m)(k'+m')}\, f^{k-\frac{1}{2},k'-\frac{1}{2}}_{m+\frac{1}{2},m'-\frac{1}{2}}\right) , \end{aligned}$$
(31)

Constants \( A_{k,k'}\), \( B_{k,k'}\), \( C_{k,k'}\), \( D_{k,k'}\) are given for each concrete representation in [20]. From (30) we see that \(W_0\) has discrete spectrum as noted in [12]. On the other hand, the eigenvalue equation for \(W_4\) (and likewise for \(W_i\)) is quite difficult, if at all possible, to solve in this basis.

We therefore restrict to simpler problem: to find the eigenvalues of \(W^\alpha \) for a specific class of representations. The simplest possibility would be to consider Class I UIR’s (they are in the principal and complementary series): their Hilbert space representations are known, they have a lowest weight state so the coherent states can be constructed, etc. However, Class I is characterized by condition \(\,{{\mathcal {W}}}=0\): thus in our framework these UIR’s cannot be simply interpreted as de Sitter spaces: a fixed implies \(\varLambda \rightarrow \infty \).Footnote 6 Another subset which is singled out mathematically and physically is the principal continuous series. As shown in [21], in the Wigner-Inönü contraction limit these UIR’s contract to a sum of two representations of the Poincaré group with positive value of the mass-squared. The Hilbert space representations of the principal continuous series were found in [22,23,24]: we shall perform the construction explicitly in the simplest nontrivial case, \(s=1/2\).

We start from the \(s=0\,\) representation of the principal continuous series. The representation space is a direct sum of the two \(s=0\,\) representation spaces of the Poincaré algebra, [22, 23]. The states in each summand are wave functions in momentum space \(\psi (\mathbf {p})\), with the scalar product given by

$$\begin{aligned} (\psi ,\psi ^\prime )=\int \frac{d^3p}{2p_0}\, \psi ^*\psi ^\prime , \end{aligned}$$
(32)

and \( p_0=\sqrt{- p_i p^i +m^2}\). Generators of the \(\text {SO}(1,4)\) group, \(\, M_{\alpha \beta }\vert _{s=0}\equiv L_{\alpha \beta }\, \), are

$$\begin{aligned} L_{ij}&= i\left( p_i \, \frac{\partial }{\partial p^j }- p_j \, \frac{\partial }{\partial p^i } \right) \end{aligned}$$
(33)
$$\begin{aligned} L_{0i}&= ip_0\, \frac{\partial }{\partial p^i } \end{aligned}$$
(34)
$$\begin{aligned} L_{40}&= -\frac{\rho }{m}\, p_0 +\frac{1}{2m}\, \{p^i, L_{0i}\} \end{aligned}$$
(35)
$$\begin{aligned} L_{4k}&= -\frac{\rho }{m}\, p_k -\frac{1}{2m}\, \{p^0, L_{0k}\} -\frac{1}{2m}\, \{p^i, L_{ik}\}. \end{aligned}$$
(36)

They are hermitian with respect to the given scalar product, and one can easily check that \(\,W^\alpha \vert _{s=0} =0\,\), therefore \(\,{{\mathcal {W}}}=0\,\) for \(\,(\rho , s=0)\).

Higher spin representations \((\rho ,s)\) can be obtained from \((\rho , s=0)\,\) by adding spin generators \(\,S_{\alpha \beta }\) to orbital generators \(\,L_{\alpha \beta }\). Representation space will be again a direct sum of two spaces, each equivalent to the Hilbert space of the Bargmann–Wigner representation of the Poincaré group of a fixed spin s [25]. We shall here discuss the eigenvalue problem for \({s=\frac{1}{2}}\,\); the case of higher spins is more involved because of an additional projection to the highest spin states [27]. In addition, we will consider just a ‘half’ of the representation space, the other half being equivalent [24].

States for \({s=\frac{1}{2}}\,\) are Dirac bispinors in momentum space \(\psi (\mathbf {p})\) which are solutions to the Dirac equation. The Bargmann–Wigner scalar product is given by

$$\begin{aligned} (\psi ,\psi ^\prime )=\int \frac{d^3p}{\vert p_0\vert }\, \psi ^\dagger \gamma ^0\psi ^\prime =\int \frac{d^3p}{ p_0^2}\, \psi ^\dagger \psi ^\prime . \end{aligned}$$
(37)

In the Dirac representation of \(\gamma \)-matrices, \( \gamma ^0= \begin{pmatrix} I &{}\quad 0\\ 0 &{}\quad -I \end{pmatrix}\), \(\gamma ^i= \begin{pmatrix} 0 &{}\quad \sigma _i\\ -\sigma _i &{}\quad 0 \end{pmatrix} \), the states are bispinors

$$\begin{aligned} \psi (\mathbf {p}) =\begin{pmatrix} \varphi (\mathbf {p})\\ -\,\dfrac{\mathbf {p}\cdot \mathbf {\sigma }}{p_0+m}\,\varphi (\mathbf {p}) \end{pmatrix} \, \end{aligned}$$
(38)

and the scalar product reduces to

$$\begin{aligned} (\psi ,\psi ^\prime )=\int \frac{d^3p}{ p_0}\, \frac{2m}{p_0+m}\, \, \varphi ^\dagger \varphi ^\prime . \end{aligned}$$
(39)

In the chiral representation which we will use later, \( \,\tilde{\gamma }^0= \begin{pmatrix} 0 &{} I\\ I &{} 0 \end{pmatrix}\), \(\tilde{\gamma }^i= \begin{pmatrix} 0 &{} -\sigma _i\\ \sigma _i &{} 0 \end{pmatrix} \, \) and the states can be parametrized as

$$\begin{aligned} \tilde{\psi }(\mathbf {p}) =\begin{pmatrix} \tilde{\chi }(\mathbf {p})\\ \dfrac{p_0+\mathbf {p}\cdot \mathbf {\sigma }}{m}\,\tilde{\chi }(\mathbf {p}) \end{pmatrix}, \end{aligned}$$
(40)

while the scalar product becomes

$$\begin{aligned} (\psi ,\psi ^\prime )= (\tilde{\psi },\tilde{\psi }^\prime )= \int \frac{d^3p}{ p_0}\,\frac{2}{m}\,\, \tilde{\chi }^\dagger \, (p_0+\mathbf {p}\cdot \mathbf {\sigma }) \,\tilde{\chi }^\prime . \end{aligned}$$
(41)

The de Sitter group generators are given by

$$\begin{aligned} M_{ij}&= L_{ij}+S_{ij},\, \quad S_{ij}= \frac{i}{4}\, [\gamma _i,\gamma _j], \end{aligned}$$
(42)
$$\begin{aligned} M_{0i}&= L_{0i}+S_{0i}, \quad S_{0i}= \frac{i}{4}\, [\gamma _0,\gamma _i],\end{aligned}$$
(43)
$$\begin{aligned} M_{40}&= -\frac{\rho }{m}\, p_0 +\frac{1}{2m}\, \{p^i, M_{0i}\},\end{aligned}$$
(44)
$$\begin{aligned} M_{4k}&= -\frac{\rho }{m}\, p_k -\frac{1}{2m}\, \{p^0, M_{0k}\} -\frac{1}{2m}\, \{p^i, M_{ik}\}. \end{aligned}$$
(45)

One can easily check that with respect to (37) all generators are hermitian: for an operator-valued M of the \(2 \times 2\) block-form

$$\begin{aligned} M=\begin{pmatrix} A &{}\quad B\\ B &{}\quad A \end{pmatrix} \end{aligned}$$
(46)

hermiticity condition reads, in the Dirac representation of \(\gamma \)-matrices,

$$\begin{aligned} p_0^{-1} A = A^\dagger p_0^{-1}, \qquad p_0^{-1} B = - B^\dagger p_0^{-1}. \end{aligned}$$
(47)

From (33–36) we find the components \(W^\alpha \):

$$\begin{aligned} { W^0}&= \begin{pmatrix} U^0 &{}\quad V^0 \\ V^0 &{}\quad U^0 \end{pmatrix}, \end{aligned}$$
(48)
$$\begin{aligned} { W^i}&= \begin{pmatrix} U^i &{}\quad V^i \\ V^i &{}\quad U^i \end{pmatrix}, \end{aligned}$$
(49)
$$\begin{aligned} { W^4}&= -\frac{1}{2} \begin{pmatrix} i p_0\, \frac{\partial }{\partial p^i}\sigma ^i &{}\quad \epsilon ^{ijk} p_i\, \frac{\partial }{\partial p^j}\, \sigma _k + \frac{3i}{2} \\ \epsilon ^{ijk} p_i\, \frac{\partial }{\partial p^j}\, \sigma _k + \frac{3i}{2} &{}\quad i p_0\, \frac{\partial }{\partial p^i}\sigma ^i \end{pmatrix} \end{aligned}$$
(50)

with

$$\begin{aligned} U^0&= -\frac{1}{2m} \left( \left( \rho - \frac{i}{2} \right) \, p_i\sigma ^i +i\, p_0^2\, \frac{\partial }{\partial p^i}\sigma ^i \right) \\ V^0&= -\frac{1}{2m} \left( \epsilon ^{ijk}p_0p_i\, \frac{\partial }{\partial p^j}\, \sigma _k + \frac{3i}{2}\, p_0 \right) \\ U^i&= \frac{p_0}{2m}\left( -i p^i\frac{\partial }{\partial p_k}\,\sigma _k +\left( \rho -\frac{i}{2} \right) \, \sigma ^i \right) , \\ V^i&=\frac{1}{2m}\left( -2i p^i +i\epsilon ^{ijk}p_l M_{jk}\sigma ^l \right. \\&\quad \left. +\,\epsilon ^{ijk} \left( i\rho p_j- p_lp^l \frac{\partial }{\partial p^j} - p_jp_l \frac{\partial }{\partial p_l} \right) \sigma _k \right) . \end{aligned}$$

We have seen already in (30) that the spectrum of \(W^0\,\) is discrete in every UIR of the \(\text {SO}(1,4)\) group, and that the eigenvalues are \(\, k'(k'+1)-k(k+1)\, \). On the other hand, due to de Sitter symmetry, spatial directions i and 4 are equivalent: therefore \(W^4\) and \(W^i\) have the same spectra. We can thus confine to the eigenvalue problem of \(W^4\).

We proceed as follows. First, we observe that in the Dirac representation \(W^4\) has the form (46) with

$$\begin{aligned} A= -\frac{i}{2}\, p_0\, \frac{\partial }{\partial p^i}\sigma ^i, \qquad B=-\frac{1}{2} \left( \epsilon ^{ijk} p_i\, \frac{\partial }{\partial p^j}\, \sigma _k + \frac{3i}{2}\right) .\nonumber \\ \end{aligned}$$
(51)

Unitary transformation to the chiral representation transforms \(W^4\) to

$$\begin{aligned} {\tilde{W}}^4= UW^4U^\dagger = \begin{pmatrix} A + B &{}\quad 0\\ 0 &{}\quad A - B \end{pmatrix}, \end{aligned}$$
(52)

where \(\, U = \dfrac{1}{\sqrt{2}} \begin{pmatrix} I &{}\quad I\\ I &{}\quad -\,I \end{pmatrix} \,\). This means that we can solve the eigenvalue problems for \(A+B\) and \(A-B\) separately. But in fact, one can easily check that if \(\, \tilde{\chi }\,\) satisfies

$$\begin{aligned} (A+B)\, \tilde{\chi }= \lambda \, \tilde{\chi }, \end{aligned}$$
(53)

the other spinor component of the eigenvalue equation,

$$\begin{aligned} (A-B)\, \tilde{\chi }= \lambda \,\, \dfrac{p_0+\mathbf {p}\cdot \mathbf {\sigma }}{m}\, \tilde{\chi }, \end{aligned}$$
(54)

is automatically satisfied for A, B given by (51).

Since \(W^4\) commutes with the generators of 3-rotations, we can diagonalize \(A+B\,\) simultaneously with \(M_{ij}\), that is we can write the eigenfunctions in the form

$$\begin{aligned} \tilde{\chi }(p,\theta ,\varphi ) = \frac{f(p)}{p}\, \phi _{jm}(\theta ,\varphi )+\frac{h(p)}{p}\, \chi _{jm}(\theta ,\varphi ), \end{aligned}$$
(55)

where p is the radial momentum, \(\, p^2 =(p_i)^2= p_0^2 -m^2\, \) and

$$\begin{aligned}&\phi _{jm} (\theta ,\varphi )= \begin{pmatrix} \sqrt{\frac{j+m}{2j}}\,\, Y_{j-1/2}^{m-1/2}(\theta ,\varphi ) \\ \sqrt{\frac{j-m}{2j}}\, \,Y_{j-1/2}^{m+1/2}(\theta ,\varphi ) \end{pmatrix}, \\&\chi _{jm} (\theta ,\varphi )= \begin{pmatrix} \sqrt{\frac{j+1-m}{2(j+1)}}\, \,Y_{j+1/2}^{m-1/2} (\theta ,\varphi )\\ -\sqrt{\frac{j+1+m}{2(j+1)}}\, \,Y_{j+1/2}^{m+1/2} (\theta ,\varphi ) \end{pmatrix}. \end{aligned}$$

The \(Y_l^m\) are the spherical harmonics. The \( \phi _{jm} \) and \( \chi _{jm} \) are orthonormal and, [26]

$$\begin{aligned} \begin{array}{ll} \phi _{jm} =\dfrac{\mathbf {p}\cdot \mathbf {\sigma }}{p} \, \chi _{jm},\qquad &{} (\mathbf {L}\cdot \mathbf {\sigma })\, \phi _{jm} = \left( j-\frac{1}{2} \right) \,\phi _{jm}, \\ \chi _{jm} =\dfrac{\mathbf {p}\cdot \mathbf {\sigma }}{p} \, \phi _{jm}, &{} (\mathbf {L}\cdot \mathbf {\sigma })\, \chi _{jm} = -\left( j+\frac{3}{2} \right) \,\chi _{jm}. \end{array} \end{aligned}$$
(56)

Identity \(\, (\mathbf {r}\cdot \mathbf {\sigma })(\mathbf {p}\cdot \mathbf {\sigma }) =3i+ip\,\frac{\partial }{\partial p} +i\mathbf {L}\cdot \mathbf {\sigma }\, \) is also frequently used in the calculation.

Introducing Ansatz (55), we obtain the system

$$\begin{aligned}&p_0 p\, \frac{df}{dp}-\left( j+\frac{1}{2} \right) \, p_0 f =\left( 2i\lambda +j\right) p h \end{aligned}$$
(57)
$$\begin{aligned}&p_0 p\, \frac{dh}{dp} +\left( j+\frac{1}{2} \right) \, p_0 h =\left( 2i\lambda - j-1\right) p f. \end{aligned}$$
(58)

Making the change of functions

$$\begin{aligned} f = p^{j+\frac{1}{2}} F, \qquad h = p^{-j-\frac{1}{2}} H, \end{aligned}$$
(59)

we get the first order system of equations

$$\begin{aligned} m\frac{dF}{dp_0}= & {} (2i\lambda +j)\left( \frac{p}{m} \right) ^{-2j-2}H, \end{aligned}$$
(60)
$$\begin{aligned} m \frac{dH}{dp_0}= & {} (2i\lambda -j-1) \left( \frac{p}{m} \right) ^{2j}F . \end{aligned}$$
(61)

The corresponding second-order equations for F and H are

$$\begin{aligned}&p^2 \frac{d^2 F}{dp_0^2} +2(j+1)p_0 \frac{d F}{dp_0} -(2i\lambda +j)(2i\lambda -j-1)F =0, \end{aligned}$$
(62)
$$\begin{aligned}&p^2 \,\frac{d^2 H}{dp_0^2} -2j p_0\,\frac{d H}{dp_0} -(2i\lambda +j)(2i\lambda -j-1) H =0. \end{aligned}$$
(63)

These equations can be transformed to the Legendre equation by an additional change of functions. Introducing \(x={p_0}/{m}\) and

$$\begin{aligned} F=(x^2-1)^{-\frac{j}{2}}\,{\tilde{F}},\qquad H=(x^2-1)^{ \frac{j+1}{2} }\,{\tilde{H}}, \end{aligned}$$
(64)

we obtain

$$\begin{aligned}&(x^2-1)\, \frac{d^2{\tilde{F}}}{dx^2} +2x\,\frac{d{\tilde{F}}}{dx} -\frac{j^2}{x^2-1}\,{\tilde{F}} = 2i\lambda (2i\lambda -1){\tilde{F}}, \end{aligned}$$
(65)
$$\begin{aligned}&(x^2-1)\, \frac{d^2 {\tilde{H}}}{dx^2} +2x\,\frac{d{\tilde{H}}}{dx} -\frac{(j+1)^2}{x^2-1}\,{\tilde{H}} = 2i\lambda (2i\lambda -1)\tilde{H}. \end{aligned}$$
(66)

Two linearly independent solutions of Legendre equation (B.3) are the associated Legendre functions \(P^\mu _\nu (x)\) and \(Q^\mu _\nu (x)\), or \(P^\mu _\nu (x)\) and \(P^{-\mu }_\nu (x)\). In our case (65–66) these solutions are

$$\begin{aligned}&{\tilde{F}}(x) = {\tilde{A}} \,P^j_{-2i\lambda }(x)= (2i\lambda +j)\tilde{B}\, P^j_{-2i\lambda }(x),\nonumber \\&{\tilde{H}}(x) ={\tilde{B}}\, P^{j+1}_{-2i\lambda }(x), \end{aligned}$$
(67)

and

$$\begin{aligned}&{\tilde{F}}(x) = A\, P^{-j}_{-2i\lambda }(x),\nonumber \\&{\tilde{H}}(x) = B\, P^{-j-1}_{-2i\lambda }(x) = A\, (2i\lambda -j-1)\, P^{-j-1}_{-2i\lambda }(x). \end{aligned}$$
(68)

Relations between coefficients \(\,{\tilde{A}}\), A and \(\,{\tilde{B}}\), B follow from (61) and the recurrence relations for the associated Legendre functions. But as shown in the Appendix, functions of the first pair (67) diverge at the point \(\,x=1\,\). Therefore there is only one normalizable solution, (68), for every real \(\,\lambda \). The corresponding radial functions f and h are equal to

$$\begin{aligned} f_{\lambda j}&=A\left( \frac{p}{m} \right) ^{\frac{1}{2}} P^{-j}_{-2i\lambda }\left( \frac{p_0}{m} \right) , \end{aligned}$$
(69)
$$\begin{aligned} h_{\lambda j}&=A\,(2i\lambda -j-1) \left( \frac{p}{m} \right) ^{\frac{1}{2}} P^{-j-1}_{-2i\lambda } \left( \frac{p_0}{m} \right) , \end{aligned}$$
(70)

and they give eigenfunctions \( \, \tilde{\psi }_{\lambda j m}\) of \(W^4\) via (55) an (40). We show in the Appendix that this set of eigenfunctions is complete: \( \, \tilde{\psi }_{\lambda j m}\) are orthogonal and normalized to \(\delta \)-function,

$$\begin{aligned} \left( \tilde{\psi }_{\lambda j m},\tilde{\psi }_{\lambda ^\prime j^\prime m^\prime } \right)&= \, 2A^* A^\prime \nonumber \\&\frac{\varGamma (\frac{1}{2} -2i\lambda )\, \varGamma (\frac{1}{2} + 2i\lambda ^\prime )}{\varGamma (j+1 -2i\lambda )\, \varGamma (j+1 + 2i\lambda ^\prime )}\nonumber \\&\delta _{m m^\prime }\, \delta _{j j^\prime }\,\delta (\lambda -\lambda ^\prime ), \end{aligned}$$
(71)

so the normalization and the phases can be fixed as

$$\begin{aligned} A= \frac{\varGamma (j+1 + 2i\lambda )}{\sqrt{2}\, \varGamma (\frac{1}{2} + 2i\lambda )}. \end{aligned}$$
(72)

4 Group-theoretic view

In the previous section we solved the eigenvalueproblem of \(W^4\) in \((\rho , s=\frac{1}{2})\) UIR of the principal continuous series of \(\text {SO}(1,4)\) using the Hilbert space representation [22, 23]. But this problem could have been solved using the results of representation theory. Namely, the embedding coordinates, components of the ‘Pauli–Lubanski’ vector \(W^\alpha \), coincide in fact with one of the two quadratic Casimir operators of the subgroups of \(\text {SO}(1,4)\): \(W^0\) is a Casimir operator of \(\text {SO}(4)\) while \(W^4\) and \(W^i\) are Casimir operators of \(\text {SO}(1,3)\) subgroups.Footnote 7 This can be easily seen from their definition:

$$\begin{aligned} W^0&=\frac{1}{8}\, \epsilon ^{0\alpha \beta \gamma \delta } M_{\alpha \beta } M_{\gamma \delta } = \frac{1}{4}\, \epsilon ^{ijk}(M_{ij} M_{4k}+M_{4k}M_{ij}) \end{aligned}$$
(73)
$$\begin{aligned} W^4&=\frac{1}{8}\, \epsilon ^{4\alpha \beta \gamma \delta } M_{\alpha \beta } M_{\gamma \delta } =- \frac{1}{4}\, \epsilon ^{ijk}(M_{ij} M_{0k}+M_{0k}M_{ij}) \end{aligned}$$
(74)

where \(\, \epsilon _{0ijk4}=\epsilon _{ijk}\). As \(W^0\) is a Casimir operator of the compact group \(\text {SO}(4)\), it has discrete eigenvalues which are equal to \(\,k'(k'+1) - k(k+1)\). On the other hand, to find the eigenvalues of \(W^4\) one has to decompose representation \((\rho ,s)\) or \((\rho ,s=\frac{1}{2})\) of the principal continuous series of \(\text {SO}(1,4)\) into the UIR’s of its subgroup \(\text {SO}(1,3)\). This was done by Ström, and the resulting decomposition of the representation space, \(\, \mathcal{H}^s={{\mathcal {H}}}^{s+} \oplus {{\mathcal {H}}}^{s-}\), is in [28] written as

$$\begin{aligned} {{\mathcal {H}}}^{s\pm }&= \frac{1}{(2\pi ^4)^{2}}\int \limits _0^{\infty } \sum _{s_0=\pm s,\pm (s-1),\dots } {{\mathcal {H}}}^{s\pm }(s_0,\nu ) \, (s_0^2+\nu ^2) \, d\nu \, \nonumber \\&=\frac{1}{(2\pi ^4)^{2}} \int \limits _{-\infty }^{\infty } \sum _{s_0= s,s-1,\dots } {{\mathcal {H}}}^{s\pm }(s_0,\nu ) \, (s_0^2+\nu ^2) \, d\nu \, \end{aligned}$$
(75)

where \(s_0\) and \(\nu \) label the UIR’s of the Lorentz group. The representation space of the \((\rho , s)\) representation is decomposed into a direct integral and sum of unitary irreducible representations \(\,(\nu , s_0)\) of \(\text {SO}(1,3)\): \(\nu \in (-\infty , +\infty )\) is continuous and \(s_0\), \(\vert s_0\vert \le s\), is discrete. The eigenvalue of \(W^0\) which corresponds to each of the representations in decomposition (75) is equal to \(\,s_0\nu \).

Our result for \(s=\frac{1}{2}\) is in accordance with this. There is only one summand in (75) corresponding to \(\, s_0=s=\frac{1}{2}\); the spectrum of \(W^0\) is the real axis, \(\, \lambda =\frac{\nu }{2}\in (-\infty , +\infty )\, \). An analogous decomposition of unitary irreducible representations of the Poincaré group into a direct integral of UIR’s of the Lorentz group was done in [29]: as we here use the same representation space [22, 23], there are many parallels in two calculations.

5 Summary and outlook

In this paper we continued our investigation of fuzzy de Sitter space defined as a unitary irreducible representation of the de Sitter group \(\text {SO}(1,4)\), analyzing representations of the principal continuous series. In analogy with the commutative case, fuzzy de Sitter space in four dimensions is defined as an embedding in five dimensions: the embedding coordinates are proportional to components of the Pauli–Lubanski vector, \(\,x^\alpha =\ell W^\alpha \), and the embedding relation is the Casimir relation \(\, W_\alpha W^\alpha \)= const. By an explicit calculation in the \(\,(\rho ,s=\frac{1}{2})\) representation we found that the spectrum of time \(x^0\) is discrete while the spectra of spacelike coordinates \(x^4\) and \(x^i\) are continuous. This result is in fact general and holds for all principal continuous UIR’s \(\,(\rho ,s)\) of the \(\,\text {SO}(1,4)\), which can be proved by using the result [28] for the decomposition of representations of the principal series of \(\text {SO}(1,4)\) into the UIR’s its \(\text {SO}(1,3)\) subgroup.

There are other operators, that is other coordinates on fuzzy de Sitter space whose properties one would like to understand and physically interpret. First of them is certainly the cosmological time, \(\, \tau = -\ell \log \, (W^0+W^4)\), and second are the isotropic coordinates. While it is, at least in the \(\,(\rho ,s=\frac{1}{2})\) representation, straightforward to write the eigenvalueproblem for \(\tau \), the corresponding differential equation turns out to be not easy to solve. This is one of the problems in the given setup which deserves additional work and which might give interesting results.

The given construction of fuzzy de Sitter space can be straightforwardly generalized to other spaces of maximal symmetry with the symmetry groups \(\text {SO}(p,q)\), in particular for even-dimensional spaces, \(\, p+q=d+1\,\) with even \(\,d\). In these cases, embedding coordinates can, as for \(d=4\), be identified with the highest W-symbol,

$$\begin{aligned} W^\alpha = \epsilon ^{\alpha \alpha _1 \alpha _2\dots \alpha _{d-1}\alpha _d} M_{\alpha _1\alpha _2}\dots M_{\alpha _{d-1}\alpha _d}, \end{aligned}$$
(76)

which is a vector in a \((d+1)\)-dimensional flat space. The embedding relation is the Casimir relation \(\,W_\alpha W^\alpha \)= const, and the appropriate fuzzy space is then defined as an UIR of the \(\text {SO}(p,q)\) group. Further, \(W^\alpha \) are the Casimir operators of subgroups \(\text {SO}(p-1,q)\) and \(\text {SO}(p,q-1)\) and their properties are in large part determined by the group theory. On the other hand for fuzzy Lorentzian spaces, particularly interesting are the \(\text {SO}(1,d)\) groups which describe conformal symmetry in \(\,d-1\,\) dimensions. Their representation theory is well studied, in particular, the decomposition formulas for the UIR’s of the principal continuous series, [30, 31] are known. Moreover, the algebra of the conformal group has the same structure that was used to define differential calculus for fuzzy de Sitter space in four dimensions. Clearly, for arbitrary dimension \(\, d\) momenta can be defined analogously to (27), as generators of translations of the conformal group,

$$\begin{aligned} i{\tilde{p}}_0 \sim M_{0d},\qquad i{\tilde{p}}_i \sim M_{id}+M_{0i}\, , \quad i=1,2,\dots d-1.\nonumber \\ \end{aligned}$$
(77)

The \(\,{\tilde{p}}_i\) mutually commute; the differential structure which corresponds to this choice of the moving frame gives, in the commutative limit, metric of the de Siter space in d dimensions. Therefore, a general construction with common general properties exists and should be further explored.