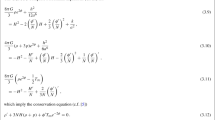One must be prepared to follow up the consequence of theory, and feel that one just has to accept the consequences no matter where they lead.
Paul Dirac
Our mistake is not that we take our theories too seriously, but that we do not take them seriously enough.
Steven Weinberg.
Abstract
Upon treating the whole closed string massless sector as stringy graviton fields, Double Field Theory may evolve into Stringy Gravity, i.e. the stringy augmentation of General Relativity. Equipped with an \(\mathrm {O}(D,D)\) covariant differential geometry beyond Riemann, we spell out the definition of the energy–momentum tensor in Stringy Gravity and derive its on-shell conservation law from doubled general covariance. Equating it with the recently identified stringy Einstein curvature tensor, all the equations of motion of the closed string massless sector are unified into a single expression, \(G_{AB}=8\pi G T_{AB}\), which we dub the Einstein Double Field Equations. As an example, we study the most general \({D=4}\) static, asymptotically flat, spherically symmetric, ‘regular’ solution, sourced by the stringy energy–momentum tensor which is nontrivial only up to a finite radius from the center. Outside this radius, the solution matches the known vacuum geometry which has four constant parameters. We express these as volume integrals of the interior stringy energy–momentum tensor and discuss relevant energy conditions.
Similar content being viewed by others
1 Introduction
The Einstein–Hilbert action is often referred to as ‘pure’ gravity, as it is formed by the unique two-derivative scalar curvature of the Riemannian metric. Minimal coupling to matter follows unambiguously through the usual covariant derivatives,
which ensures covariance under both diffeomorphisms and local Lorentz symmetry. In the words of Cheng-Ning Yang, symmetry dictates interaction. The torsionless Christoffel symbols of the connection and the spin connection are fixed by the requirement of compatibility with the metric and the vielbein. The existence of Riemann normal coordinates supports the Equivalence Principle, as the Christoffel symbols vanish pointwise. Needless to say, in General Relativity (GR), the metric is privileged to be the only geometric and thus gravitational field, on account of the adopted differential geometry a la Riemann, while all other fields are automatically categorized as additional matter.
String theory may put some twist on this Riemannian paradigm. First of all, the metric is merely one segment of closed string massless sector which consists of a two-form gauge potential, \(B_{\mu \nu }\), and a scalar dilaton, \(\phi \), in addition to the metric, \(g_{\mu \nu }\). A genuine stringy symmetry called T-duality then converts one to another [1, 2]. Namely, the closed string massless sector forms multiplets of \(\mathbf {O}(D,D)\) T-duality. This may well hint at the existence of Stringy Gravity as an alternative to GR, which takes the entire massless sector as geometric and therefore gravitational. In recent years this idea has been realized concretely through the developments of so-called Double Field Theory (DFT) [3,4,5,6,7,8]. The relevant covariant derivative has been identified [9, 10] and reads schematically,
where \(\Gamma _{A}\) is the DFT version of the Christoffel symbols for generalized diffeomorphisms, while \(\Phi _{A}\) and \({{\bar{\Phi }}}_{A}\) are the two spin connections for the twofold local Lorentz symmetries, \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\). They are compatible with, and thus formed by, the closed string massless sector, containing in particular the H-flux (\(H=\mathrm{d}B\)). The doubling of the spin group implies the existence of two separate locally inertial frames for left and right closed string modes, respectively [11]. In a sense, it is a prediction of DFT (and also Generalized Geometry [12]) that there must in principle exist two distinct kinds of fermions [13]. The DFT-Christoffel symbols constitute DFT curvatures: scalar and ‘Ricci’. The scalar curvature naturally defines the pure DFT Lagrangian in analogy with GR. However, in Stringy Gravity the Equivalence Principle is generically broken [13, 14]: there exist no normal coordinates in which the DFT-Christoffel symbols would vanish pointwise. This should not be a surprise since, strictly speaking, the principle holds only for a point particle and does not apply to an extended object like a string, which is subject to ‘tidal forces’ via coupling to the H-flux.
Beyond the original goal of reformulating supergravities in a duality-manifest framework, DFT turns out to have quite a rich spectrum. It describes not only the Riemannian supergravities but also various non-Riemannian theories in which the Riemannian metric cannot be defined [15], such as non-relativistic Newton–Cartan or ultra-relativistic Carroll gravities [16], the Gomis–Ooguri non-relativistic string [17, 18], and various chiral theories including the one by Siegel [19]. Without resorting to Riemannian variables, supersymmetrizations have been also completed to the full order in fermions, both on target spacetime [20, 21] and on worldsheet [22].
Combining the scalar and ‘Ricci’ curvatures, the DFT version of the Einstein curvature, \(G_{AB}\), which is identically conserved, \(\mathcal{D}_{A}G^{A}{}_{B}=0\), and generically asymmetric, \(G_{AB}\ne G_{BA}\), has been identified [23]. Given this identification, it is natural to anticipate the ‘energy–momentum’ tensor in DFT, say \(T_{AB}\), which should counterbalance the stringy Einstein curvature through the Einstein Double Field Equations, i.e. the equations of motion of the entire closed string massless sector as the stringy graviton fields,
where G (without any subscript index) denotes Newton’s constant. For consistency, the stringy energy–momentum tensor should be asymmetric, \(T_{AB}\ne T_{BA}\), and conserved, \(\mathcal{D}_{A}T^{A}{}_{B}= 0\), especially on-shell, i.e. up to the equations of motion of the additional matter fields.
In order to compare the ‘gravitational’ aspects of DFT and GR, circular geodesic motions around the most general spherically symmetric solution to ‘\({G_{AB}=0}\)’ have been studied in [24] for the case of \({D=4}\). While the solution was a re-derivation of a previously known result in the supergravity literature [25], the new interpretation was that it is the ‘vacuum’ solution to DFT, with the right-hand side of (1.3) vanishing: it is analogous to the Schwarzschild solution in GR. The DFT spherical vacuum solution turns out to have four (or three, up to a radial coordinate shift) free parameters, in contrast to the Schwarzschild geometry which possesses only one free parameter, i.e. mass. With these extra free parameters, DFT modifies GR at ‘short’ scales in terms of the dimensionless parameter R / (MG), i.e. the radial distance normalized by the mass times Newton’s constant. For large R / (MG), DFT converges to GR, but for finite R / (MG) they differ generically. It is an intriguing fact that the dark matter and dark energy problems all arise from astronomical observations at smaller \(R/(MG) \lesssim 10^{7}\), corresponding to long distance divided by far heavier mass [14, 24]. Such a ‘uroboros’ spectrum of R / (MG) is listed below in natural units.

The purpose of the present paper is twofold: (i) to propose the definition of the stringy energy–momentum tensor which completes the Einstein Double Field Equations spelled out in (1.3), and (ii) to analyze the most general spherically symmetric \({D=4}\) ‘regular’ solution which will teach us the physical meanings of the free parameters appearing in the vacuum solution of [24, 25]. The rest of the paper is organized as follows.
-
We start Sect. 2 by reviewing DFT as Stringy Gravity. We then consider coupling to generic matter fields, propose the definition of the stringy energy–momentum tensor, and discuss its properties including the conservation law. Some examples will follow.
-
In Sect. 3 we devise a method to address isometries in the vielbein formulation of Stringy Gravity. We generalize the known generalized Lie derivative one step further, to a ‘further-generalized Lie derivative’, which acts not only on \(\mathbf {O}(D,D)\) vector indices but also on all the \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) local Lorentz indices.
-
Section 4 is devoted to the study of the most general, asymptotically flat, spherically symmetric, static ‘regular’ solution to the \({D=4}\) Einstein Double Field Equations. We postulate that the stringy energy–momentum tensor is nontrivial only up to a finite cutoff radius, \(r_{\mathrm{c}}\). While we recover the vacuum solution of [24] for \(r>r_{\mathrm{c}}\), we derive integral expressions for its constant parameters in terms of the stringy energy–momentum tensor for \(r<r_{\mathrm{c}}\), and discuss relevant energy conditions.
-
We conclude with our summary and comments in Sect. 5.
-
In “Appendix A” we collect some known features of GR, such as the general properties of the energy–momentum tensor and the most general spherically symmetric (Schwarzschild type) regular solution to the undoubled Einstein Field Equations, which we double-field-theorize in the present paper.
2 Einstein double field equations
In this section we first give for completeness a self-contained review of DFT as Stringy Gravity, following which we propose the DFT, or stringy, extensions of the energy–momentum tensor and the Einstein Field Equations.
2.1 Review of DFT as stringy gravity
We review DFT following the geometrically logical – rather than historical – order: (i) conventions, (ii) the doubled-yet-gauged coordinate system with associated diffeomorphisms, (iii) the field content of stringy gravitons, (iv) DFT extensions of the Christoffel symbols and spin connection, and (v) covariant derivatives and curvatures. For complementary aspects, we refer readers to [34,35,36] as well as [37, 38].
-
Symmetries and conventions
The built-in symmetries of Stringy Gravity are as follows.
-
\(\mathbf {O}(D,D)\) T-duality
-
DFT diffeomorphisms
-
Twofold local Lorentz symmetries,Footnote 1 \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\).
We shall use capital Latin letters, \(A,B,\ldots , M,N,\ldots \) for the \(\mathbf {O}(D,D)\) vector indices, while unbarred small Latin letters, \(p,q,\ldots \) or Greek letters, \(\alpha ,\beta ,\ldots \) will be used for the vectorial or spinorial indices of \({\mathbf {Spin}(1,D{-1})}\), respectively. Similarly, barred letters denote the other \({{\mathbf {Spin}}(D{-1},1)}\) representations: \({\bar{p}},{\bar{q}},\ldots \) (vectorial) and \(\bar{\alpha },\bar{\beta },\ldots \) (spinorial). In particular, each vectorial index can be freely lowered or raised by the relevant invariant metric,
-
Doubled-yet-gauged coordinates and diffeomorphisms
By construction, functions admitted to Stringy Gravity are of special type. Let us denote the set of all the functions in Stringy Gravity by \(\mathcal{F}=\left\{ \,\Phi _{i}\,\right\} \), which should include not only physical fields but also local symmetry parameters. First of all, each function, \(\Phi _{i}(x)\), has doubled coordinates, \(x^{M}\), \(M=1,2,\ldots ,{D+D}\), as its arguments. Not surprisingly, the set is closed under addition, product and differentiation such that, if \(\,\Phi _{i}, \Phi _{j}\in \mathcal{F}\) and \(a,b\in \mathbb {R}\), then
and hence \(\Phi _{i}\) is \(C^{\infty }\). The truly nontrivial property of \(\mathcal{F}\) is that every function therein is invariant under a special class of translations: for arbitrary \(\Phi _{i},\Phi _{j},\Phi _{k}\in \mathcal{F}\),
where \(\Delta ^{M}\) is said to be derivative-index-valued. We emphasize that this very notion is only possible thanks to the built-in \(\mathbf {O}(D,D)\) group structure, whereby the invariant metric can raise the vector index of the partial derivative, \(\partial ^{M}=\mathcal{J}^{MN}\partial _{N}\). It is straightforward to showFootnote 2 that the above translational invariance is equivalent to the so-called ‘section condition’,
which is of practical utility. From (2.3), we infer that ‘physics’ should be invariant under such a shift of \(\Delta ^{M}=\Phi _{j}\partial ^{M}\Phi _{k}\). This observation further suggests that the doubled coordinates may be gauged by an equivalence relation [39],
Diffeomorphisms in the doubled-yet-gauged spacetime are then generated (actively) by the generalized Lie derivative, \({\hat{\mathcal{L}}}_{\xi }\), which was introduced initially by Siegel [4], and also later by Hull and Zwiebach [6]. Acting on an arbitrary tensor density, \(T_{M_{1}\cdots M_{n}}\in \mathcal{F}\), with weight \(\omega \), it reads
Thanks to the section condition, the generalized Lie derivative forms a closed algebra,
where the so-called C-bracket is given by
Along with this expression, it is worthwhile to note the ‘sum’,
Further, if the parameter of the generalized Lie derivative, \(\xi ^{M}\), is ‘derivative-index-valued’, the first two terms on the right-hand side of (2.6) are trivial. Moreover, if this parameter is ‘exact’ as \(\xi ^{M}=\partial ^{M}\Phi \), the generalized Lie derivative itself vanishes identically. Now, the closure (2.7) implies that the generalized Lie derivative is itself diffeomorphism-covariant:
where in the last step, from (2.8), (2.9), we have used the fact that \(\,[\zeta ,\xi ]^{M}_{{\mathrm{C}}}+{\hat{\mathcal{L}}}_{\xi }\zeta ^{M}={{\textstyle \frac{1}{2}}}\partial ^{M}(\zeta _{N}\xi ^{N})\,\), which is exact and hence null as a diffeomorphism parameter. However, if the tensor density carries additional \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) indices, e.g. \(T_{Mp{\bar{q}}\alpha \bar{\alpha }}\), its generalized Lie derivative is not local-Lorentz-covariant. Hence the generalized Lie derivative is covariant for doubled-yet-gauged diffeomorphisms but not for local Lorentz symmetries. We shall fix this limitation in Sect. 3 by further generalizing the generalized Lie derivative.
In contrast to ordinary Riemannian geometry, the infinitesimal one-form, \(\mathrm{d}x^{M}\), is not (passively) diffeomorphism covariant in doubled-yet-gauged spacetime,
Furthermore, it is not invariant under the coordinate gauge symmetry shift, \(\mathrm{d}x^{M}\ne \mathrm{d}(x^{M}+\Delta ^{M})\). However, if we gauge \(\mathrm{d}x^{M}\) explicitly by introducing a derivative-index-valued gauge potential, \(\mathcal{A}^{M}\),
we can ensure both the diffeomorphism covariance and the coordinate gauge symmetry invariance,
Utilizing the gauged infinitesimal one-form, \(Dx^{M}\), it is then possible to define the duality-covariant ‘proper length’ in doubled-yet-gauge spacetime [14, 15], and construct associated sigma models such as for the point particle [24, 42], bosonic string [40, 41], Green–Schwarz superstring [22] (and its coupling to the R–R sector [43]), exceptional string [44, 45], etc.
With the decomposition of the doubled coordinates, \(x^{M}=(\tilde{x}_{\mu },x^{\nu })\), in accordance with the form of the \(\mathbf {O}(D,D)\) invariant metric, \(\mathcal{J}_{MN}\) (2.1), the section condition reads \(\tilde{\partial }^{\mu }\partial _{\mu }=0\). Thus up to \(\mathbf {O}(D,D)\) rotations, the section condition is generically solved by setting \(\tilde{\partial }^{\mu }= 0\), removing the dependence on \(\tilde{x}_{\mu }\) coordinates. It follows that \(\mathcal{A}^{M}=A_{\lambda }\partial ^{M}x^{\lambda }=(A_{\mu },0)\) and hence the \(\tilde{x}_{\mu }\) coordinates are indeed gauged, \(Dx^{M}=(\mathrm{d}\tilde{x}_{\mu }-A_{\mu },\mathrm{d}x^{\nu })\).
-
Stringy graviton fields from the closed string massless sector
The \(\mathbf {O}(D,D)\) T-duality group is a fundamental structure in Stringy Gravity. All the fields therein must assume one representation of it, such that the \(\mathbf {O}(D,D)\) covariance is manifest.
The stringy graviton fields consist of the DFT dilaton, d, and DFT metric, \(\mathcal{H}_{MN}\). The former gives the integral measure in Stringy Gravity after exponentiation, \(e^{-2d}\), which is a scalar density of unit weight. The latter is then, by definition, a symmetric \(\mathbf {O}(D,D)\) element:
Combining \(\mathcal{J}_{MN}\) and \(\mathcal{H}_{MN}\), we acquire a pair of symmetric projection matrices,
which are orthogonal and complete,
It follows that the infinitesimal variations of the projection matrices satisfy
Further, taking the “square roots” of the projectors,
we acquire a pair of DFT vielbeins, which satisfy four defining properties:
such that (2.15) and (2.16) hold. Essentially, \((V_{M}{}^{p},{\bar{V}}_{M}{}^{{\bar{p}}})\), when viewed as a \(({D+D})\times ({D+D})\) matrix, diagonalizes \(\mathcal{J}_{MN}\) and \(\mathcal{H}_{MN}\) simultaneously into ‘\(\text{ diag }(\eta ,+\bar{\eta })\)’ and ‘\(\text{ diag }(\eta ,-\bar{\eta })\)’, respectively. The presence of twofold vielbeins as well as spin groups are a truly stringy feature, as it indicates two distinct locally inertial frames existing separately for the left-moving and right-moving closed string sectors [11], and may be a testable prediction of Stringy Gravity in itself [13].
It is absolutely crucial to note that DFT [3, 4, 8] and its supersymmetric extensions [20,21,22] are formulatable in terms of nothing but the very fields satisfying precisely the defining relations (2.14), (2.19). The most general solutions to the defining equations turn out to be classified by two non-negative integers, \((n,{\bar{n}})\). With \(1\le i,j\le n\) and \(1\le \bar{\imath },\bar{\jmath }\le {\bar{n}}\), the DFT metric is of the most general form [15],
where ((i) \(\mathcal{H}\) and \(\mathcal{K}\) are symmetric, but B is skew-symmetric, i.e. \(\mathcal{H}^{\mu \nu }=\mathcal{H}^{\nu \mu }\), \(\mathcal{K}_{\mu \nu }=\mathcal{K}_{\nu \mu }\), \(B_{\mu \nu }=-B_{\nu \mu }\); (ii) \(\mathcal{H}\) and \(\mathcal{K}\) admit kernels, \(~\mathcal{H}^{\mu \nu }X^{i}_{\nu }=\mathcal{H}^{\mu \nu }{\bar{X}}^{\bar{\imath }}_{\nu }=0\), \(~\mathcal{K}_{\mu \nu }Y_{j}^{\nu }=\mathcal{K}_{\mu \nu }{\bar{Y}}_{\bar{\jmath }}^{\nu }=0\); (iii) a completeness relation must be met, \(~\mathcal{H}^{\mu \rho }\mathcal{K}_{\rho \nu } +Y_{i}^{\mu }X^{i}_{\nu }+{\bar{Y}}_{\bar{\imath }}^{\mu }{\bar{X}}^{\bar{\imath }}_{\nu } =\delta ^{\mu }{}_{\nu }\).
It follows from the linear independence of the kernel eigenvectors that
With the section choice \({\tilde{\partial }^{\mu }= 0}\) and the parameter decomposition \(\xi ^{A}=(\tilde{\xi }_{\mu },\xi ^{\nu })\), the generalized Lie derivative, \({\hat{\mathcal{L}}}_{\xi }\mathcal{H}_{MN}\), reduces to the ordinary (i.e. undoubled) Lie derivative, \(\mathcal{L}_{\xi }\), plus B-field gauge symmetry,

Only in the case of \((n,{\bar{n}})=(0,0)\) can \(\mathcal{K}_{\mu \nu }\) and \(\mathcal{H}^{\mu \nu }\) be identified with the (invertible) Riemannian metric and its inverse. The (0, 0) Riemannian DFT metric then takes the rather well-known form,
and the corresponding DFT vielbeins read
where \(e_{\mu }{}^{p}\) and \(\bar{e}_{\mu }{}^{{\bar{p}}}\) are a pair of Riemannian vielbeins for the common Riemannian metric,
With the non-vanishing determinant, \(g=\det g_{\mu \nu }\ne 0\), the DFT dilaton can be further parametrized by
In this way, the stringy gravitons may represent the conventional closed string massless sector, \(\{g_{\mu \nu },B_{\mu \nu },\phi \}\).
Other cases of \((n,{\bar{n}})\ne (0,0)\) are then generically non-Riemannian, as the Riemannian metric cannot be defined. They include (1, 0) or \(({D-1},0)\) for non-relativistic Newton–Cartan or ultra-relativistic Carroll gravities [16], (1, 1) for the Gomis–Ooguri non-relativistic string [17, 18], and various chiral theories, e.g. [19].
For later use, it is worth noting that the two-indexed projectors generate in turn a pair of multi-indexed projectors,
satisfying

They are symmetric and traceless in the following sense:

-
Covariant derivatives with stringy Christoffel symbols and spin connections
The ‘master’ covariant derivative in Stringy Gravity,
is equipped with the stringy Christoffel symbols of the diffeomorphism connection [9],
and the spin connections for the twofold local Lorentz symmetries [10],
In the above, we set
which, ignoring any local Lorentz indices, acts explicitly on a tensor density with weight \(\omega \) as
The stringy Christoffel symbols (2.30) can be uniquely determined by requiring three properties:
- (i):
-
full compatibility with all the stringy graviton fields,
 (2.34)
(2.34)which implies, in particular,
$$\begin{aligned} \begin{array}{ll} \mathcal{D}_{A}\mathcal{J}_{BC}={\nabla }_{A}\mathcal{J}_{BC}=0,\qquad&\qquad \Gamma _{ABC}=-\Gamma _{ACB}; \end{array} \end{aligned}$$(2.35) - (ii):
-
a cyclic property (traceless condition),
$$\begin{aligned} \Gamma _{ABC}+\Gamma _{BCA}+\Gamma _{CAB}=0, \end{aligned}$$(2.36)which makes \({\nabla }_{A}\) compatible with the generalized Lie derivative (2.6) as well as the C-bracket (2.8), such that we may freely replace the ordinary derivatives therein by \({\nabla }_{A}\),
$$\begin{aligned} \begin{array}{ll} {\hat{\mathcal{L}}}_{\xi }(\partial )={\hat{\mathcal{L}}}_{\xi }({\nabla }),\qquad&\qquad [\zeta ,\xi ]_{\mathrm{C}}(\partial )=[\zeta ,\xi ]_{\mathrm{C}}({\nabla }); \end{array} \end{aligned}$$(2.37) - (iii):
-
projection constraints,
$$\begin{aligned} \begin{array}{ll} \mathcal{P}_{ABC}{}^{DEF}\Gamma _{DEF}=0,\quad&\quad \bar{\mathcal{P}}_{ABC}{}^{DEF}\Gamma _{DEF}=0, \end{array} \end{aligned}$$(2.38)which ensure the uniqueness.
Unlike the Christoffel symbols in GR, there exist no normal coordinates where the stringy Christoffel symbols would vanish pointwise. The Equivalence Principle holds for the point particle but not for the string [13, 14].
Once the stringy Christoffel symbols are fixed, the spin connections (2.31) follow immediately from the compatibility with the DFT vielbeins,
The master derivative is also compatible with the two sets of local Lorentz metrics and gamma matrices,
such that, as in GR,
The master derivative (2.29) acts explicitly as
Unsurprisingly the master derivative is completely covariant for the twofold local Lorentz symmetries. The characteristic of the master derivative, \(\mathcal{D}_{A}\), as well as \({\nabla }_{A}\) is that they are actually ‘semi-covariant’ under doubled-yet-gauged diffeomorphisms: the stringy Christoffel symbols transform as

such that \(\mathcal{D}_{A}\) and \({\nabla }_{A}\) are not automatically diffeomorphism-covariant, e.g.

Nevertheless, the potentially anomalous terms are uniquely given, or controlled, by the multi-indexed projectors, as seen in (2.43) and (2.44), such that they can be easily projected out. Completely covariantized derivatives include [9]
which can be freely pulled back by the DFT vielbeins, with \(\mathcal{D}_{p}=V^{A}{}_{p}\mathcal{D}_{A}\) and \(\mathcal{D}_{{\bar{p}}}={\bar{V}}^{A}{}_{{\bar{p}}}\mathcal{D}_{A}\), to
In particular, for a weightless vector, \(J^{A}\), it is useful to note
Furthermore, from (2.43), the following modules of the spin connections are completely covariant under diffeomorphisms:
Consequently, acting on \({\mathbf {Spin}(1,D{-1})}\) spinors, \(\rho ^{\alpha }\), \(\psi _{{\bar{p}}}^{\alpha }\), or \({{\mathbf {Spin}}(D{-1},1)}\) spinors, \(\rho ^{\prime \bar{\alpha }}\), \(\psi ^{\prime \bar{\alpha }}_{p}\), the completely covariant Dirac operators are, with respect to both diffeomorphisms and local Lorentz symmetries [10, 20],
For a \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) bi-fundamental spinorial field or the Ramond–Ramond potential, \(\mathcal{C}^{\alpha }{}_{\bar{\alpha }}\), a pair of completely covariant nilpotent derivatives, \(\mathcal{D}_{+}\) and \(\mathcal{D}_{-}\), can be defined [46] (c.f. [47]),
where, with (2.41), \(\mathcal{D}_{A}\mathcal{C}=\partial _{A}\mathcal{C}+\Phi _{A}\mathcal{C}-\mathcal{C}{{\bar{\Phi }}}_{A}\). Specifically, the R–R field strength is given by \(\mathcal{F}=\mathcal{D}_{+}\mathcal{C}\).
Finally, for a Yang–Mills potential, \({\mathbf {A}}_{M}\), the completely covariant field strength reads [48]
In order to recover the standard (undoubled) physical degrees of freedom, one should impose additional “section conditions” on the doubled Yang–Mills gauge potential [13],
It turns out that the standard field strength,
then becomes completely covariant, and (2.51) reduces to
Upon Riemannian backgrounds (2.23), (2.25), the spin connections (2.48) reduce explicitly to
where, generalizing (1.1), we have \(\omega _{\mu pq}=e_{p}{}^{\nu }(\partial _{\mu }e_{\nu q}-\gamma _{\mu }^{\lambda }{}_{\nu }e_{\lambda q})\), \(~{\bar{\omega }}_{\mu {\bar{p}}{\bar{q}}}=\bar{e}_{{\bar{p}}}{}^{\nu }(\partial _{\mu }\bar{e}_{\nu {\bar{q}}}-\gamma _{\mu }^{\lambda }{}_{\nu }\bar{e}_{\lambda {\bar{q}}})\), and
-
Curvatures: stringy Einstein tensor
The semi-covariant Riemann curvature in Stringy Gravity is defined by [9]
where \(\Gamma _{ABC}\) are the stringy Christoffel symbols (2.30) and \(R_{ABCD}\) denotes their “field strength”,
Crucially, by construction, it satisfies symmetric properties and an algebraic “Bianchi” identity,Footnote 3
Furthermore, just like the Riemann curvature in GR (A.14), it transforms as ‘total’ derivatives under the arbitrary variation of the stringy Christoffel symbols,Footnote 4
In particular, it is ‘semi-covariant’ under doubled-yet-gauged diffeomorphisms,

In DFT there is no completely covariant four-indexed ‘Riemann’ curvature [9, 51], which is in a sense consistent with the absence of ‘normal’ coordinates for strings. The completely covariant ‘Ricci’ and scalar curvatures are then, with \(S_{AB}=S_{BA}=S^{C}{}_{ACB}\),
These completely covariant curvatures contain both \(\mathcal{H}_{MN}\) and d, as is the case for the connection, \(\Gamma _{LMN}\) (2.30). The DFT metric alone cannot generate any covariant curvature c.f. [49].
It is worth noting the identities
and the commutation relations [12, 50]
Combining the ‘Ricci’ and the scalar curvatures, it is possible to construct the stringy ‘Einstein’ tensor which is covariantly conserved [23],
From (2.45), this conservation law is completely covariant. Note also that in general, \(G_{AB}\ne G_{BA}\,\) and \(\,{\nabla }_{B}G^{AB}\ne 0\,\). However, we may symmetrize the stringy Einstein tensor, still preserving the conservation law, by multiplying the DFT metric from the right,
Since \(G_{A}{}^{A}=-DS_{\scriptscriptstyle {{(0)}}}\), the vanishing of the stringy Einstein tensor, \({G_{AB}\equiv 0}\), is equivalent to the separate vanishing of the ‘Ricci’ and the scalar curvatures, \({S_{p{\bar{q}}}\equiv 0}\) and \({S_{\scriptscriptstyle {{(0)}}}\equiv 0}\), respectively, which correspond to the original DFT equations of motion [3, 8].
Restricting to Riemannian backgrounds (2.23), (2.25), we have explicitly,
In particular, the upper left \(D{\times D}\) diagonal block of \((G\mathcal{H})_{AB}\) contains the undoubled Einstein tensor in GR,
2.2 Stringy energy–momentum tensor & Einstein double field equations
We now consider Stringy Gravity coupled to generic matter fields, in analogy to GR (A.1),
where \(L_{\mathrm{matter}}\) is the \(\mathbf {O}(D,D)\) symmetric Lagrangian of the matter fields, \(\Upsilon _{a}\), equipped with the completely covariantized derivatives, \(\mathcal{D}_{M}\). Some examples will follow below in subsection 2.2.1, including cases (2.118), (2.125), (2.129) where the Lagrangian density, \(\mathcal{L}_{\mathrm{matter}}\equiv e^{-2d}L_{\mathrm{matter}}\), does not contain, and hence decouples from, the DFT dilaton, d. The integral is taken over a D-dimensional section, \(\Sigma \), corresponding to a ‘gauge slice’, c.f. (2.5). We seek the variation of the above action which is induced by the arbitrary transformations of all the fields, \(\delta d\), \(\delta P_{AB}\), \(\delta {\bar{P}}_{AB}\), \(\delta V_{Ap}\), \(\delta {\bar{V}}_{A{\bar{p}}}\), and \(\delta \Upsilon _{a}\). They are subject to the following algebraic relations, originating from the defining properties the stringy graviton fields, (2.14), (2.15), (2.19),
Firstly, as is known [9], the pure Stringy Gravity term transforms, from (2.34), (2.59), (2.60), (2.62), as
of which the total derivative can be ignored in the variation of the action.
Secondly, in a similar fashion to (A.12), the (local-Lorentz-symmetric) matter Lagrangian transforms, up to total derivatives (\(\simeq \)), as
where \(\frac{\delta L_{\mathrm{matter}}}{\delta \Upsilon _{a}}\) corresponds to the Euler–Lagrange equation for each matter field, \(\Upsilon _{a}\), and \(\delta ^{\prime }\Upsilon _{a}\) is the arbitrary variation of the matter field, i.e. \(\delta \Upsilon _{a}\), supplemented by the infinitesimal local Lorentz rotations set by the parameters \(\delta V_{C[p}V^{C}{}_{q]}\) and \(\delta {\bar{V}}_{C[{\bar{p}}}{\bar{V}}^{C}{}_{{\bar{q}}]}\). Eq. (2.73) holds since \(L_{\mathrm{matter}}\) is supposed to be \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) local Lorentz symmetric and therefore the second terms in the variations of the DFT vielbeins in (2.71) can be inversely traded with the \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) local Lorentz transformations of the matter fields, which justifies to the change \(\delta \Upsilon _{a}\rightarrow \delta ^{\prime }\Upsilon _{a}\).
The variation (2.73) suggests the following two definitions,
both of which will constitute the conserved energy–momentum tensor in Stringy Gravity, see (2.85). We stress that to avoid any ambiguity, the functional derivatives are best computed from the infinitesimal variation of the Lagrangian.
Equation (2.73) then reads
It is worthwhile to note that, for the restricted cases of \(L_{\mathrm{matter}}\) in which the DFT vielbeins are absent and only the projectors are present, we have
and, from (2.71), the above definition of \(K_{p{\bar{q}}}\) reduces to
Now, collecting all the results of (2.71), (2.72) and (2.74), the variation of the action (2.70) reads, disregarding any surface integrals,
All the equations of motion are then given by
where ‘\(\equiv \)’ is used to denote the on-shell equations for the matter fields. Specifically, when the variation is generated by doubled-yet-gauged diffeomorphisms, we have
and, from \(\mathcal{D}_{B}V_{Ap}=0\) (2.39),
which implies
Substituting these results into (2.78), utilizing the invariance of the action under doubled-yet-gauged diffeomorphisms while neglecting surface terms, we achieve a crucial result,
This leads to the definitions of the off-shell conserved stringy Einstein curvature tensor (2.66) from [23],
and separately the on-shell conserved energy–momentum tensor in Stringy Gravity,
NoteFootnote 5 \(T_{AB}\ne T_{BA}\,\) and \(\,\mathcal{D}_{B}T^{AB}\ne 0\,\). However, like \((G\mathcal{H})_{AB}=(G\mathcal{H})_{BA}\) (2.67), we may symmetrize the stringy energy–momentum tensor,
\(G_{AB}\) and \(T_{AB}\) each have \({D^{2}+1}\) components, given by
respectively. The equations of motion of the DFT vielbeins and the DFT dilaton are unified into a single expression, the Einstein double field equations,
which is naturally consistent with the central idea that Stringy Gravity treats the entire closed string massless sector as geometrical stringy graviton fields.
From (2.80), (2.82) and (2.85), if we contract the stringy energy–momentum tensor with an \(\mathbf {O}(D,D)\) vector, its divergence reads
Therefore, if \(\xi ^{A}\) is a DFT-Killing vector satisfying the DFT-Killing equations [23],
the contraction \(T^{A}{}_{B}\xi ^{B}\) gives an on-shell conserved Noether current (from (2.47)),
and the corresponding Noether charge,
where the superscript index, t, denotes the time component for a chosen section. It is worthwhile to note that the alternative contraction with the symmetrized energy–momentum tensor, \((T\mathcal{H})^{A}{}_{B}\xi ^{B}\), is not conserved even if \(\xi ^{A}\) is a Killing vector.
Through contraction with the DFT vielbeins, the conservation law of the energy–momentum tensor decomposes into two separate formulae,
Restricting to Riemannian backgrounds (2.23), (2.25), with \({\bigtriangledown }_{\mu }=\partial _{\mu }+\gamma _{\mu }+\omega _{\mu }+{\bar{\omega }}_{\mu }\) (2.56), we have
and
Thus, the conservation law reduces to the following two sets of equations,
In fact, for the above computations, we first put, c.f. (2.57),
and then let the Greek indices of \(K_{\mu \nu }\) be raised by the Riemannian metric (2.24), \(g^{\mu \nu }=e_{p}{}^{\mu }e^{p\nu }=-\bar{e}_{{\bar{p}}}{}^{\mu }\bar{e}^{{\bar{p}}\nu }\):
It follows that
and
The Einstein Double Field Equations (2.88) reduce, upon Riemannian backgrounds (2.23), (2.68), to
These also imply the two reduced conservation laws, (2.96) and (2.97), as \({\mathcal{D}_{A}G^{AB}}=0\) is an off-shell identity. Explicitly, we have
which implies the second conservation law (2.97). On the other hand, solving \(R_{\mu \nu }\) and \(R\,\) from (2.102) and (2.104) respectively, we get
where we have used the identity \(\Box \partial _{\nu }\phi -{\bigtriangledown }_{\nu }\Box \phi =R_{\nu \rho }\partial ^{\rho }\phi \,\). The last three lines in (2.106) vanish separately up to (2.102), (2.103), and the closedness of the H-flux. Therefore, we recover the first conservation law (2.96) as the vanishing of the first line on the right-hand side of the equality above.
2.2.1 Examples
Here we list various matter fields coupled to Stringy Gravity and write down their contributions to the stringy energy–momentum tensor (2.85), (2.101).
-
Cosmological constant
In Stringy Gravity, the cosmological constant term is given by a constant, \(\Lambda _{\mathrm{DFT}}\), times the integral measure, \(e^{-2d}\) [9],
$$\begin{aligned} \textstyle {\frac{1}{16\pi G}}e^{-2d}\left( S_{\scriptscriptstyle {{(0)}}}-2\Lambda _{\mathrm{DFT}}\right) . \end{aligned}$$(2.107)The corresponding energy–momentum tensor is
$$\begin{aligned} T_{AB}=-\textstyle {\frac{1}{8\pi G}}\mathcal{J}_{AB}\Lambda _{\mathrm{DFT}}, \end{aligned}$$(2.108)such that \(K_{p{\bar{q}}}=0\) and \(T_{\scriptscriptstyle {{(0)}}}=\frac{1}{4\pi G}\Lambda _{\mathrm{DFT}}\).
-
Scalar field
A free scalar field in Stringy Gravity is described by, e.g. [13],
$$\begin{aligned} L_{\Phi }= & {} -{{\textstyle \frac{1}{2}}}\mathcal{H}^{MN}\partial _{M}\Phi \partial _{N}\Phi -{{\textstyle \frac{1}{2}}}m_{\scriptscriptstyle {\Phi }}^{2}\Phi ^{2}\nonumber \\= & {} {{\textstyle \frac{1}{2}}}({\bar{P}}^{MN}-P^{MN})\partial _{M}\Phi \partial _{N}\Phi -{{\textstyle \frac{1}{2}}}m_{\scriptscriptstyle {\Phi }}^{2}\Phi ^{2}. \end{aligned}$$(2.109)It is straightforward to see, with \(\partial _{p}\equiv V^{A}{}_{p}\partial _{A}\), \(\partial _{{\bar{q}}}\equiv {\bar{V}}^{A}{}_{{\bar{q}}}\partial _{A}\),
$$\begin{aligned} K_{p{\bar{q}}}= & {} \partial _{p}\Phi \partial _{{\bar{q}}}\Phi , \nonumber \\ T_{\scriptscriptstyle {{(0)}}}= & {} \mathcal{H}^{MN}\partial _{M}\Phi \partial _{N}\Phi +m_{\scriptscriptstyle {\Phi }}^{2}\Phi ^{2} =-2L_{\Phi }. \end{aligned}$$(2.110)For Riemannian backgrounds (2.23), (2.25), and the section choice \({\tilde{\partial }^{\mu }=0}\), we have \(\partial _{p}=\frac{1}{\sqrt{2}}e_{p}{}^{\mu }\partial _{\mu }\), \(\partial _{{\bar{q}}}=\frac{1}{\sqrt{2}}\bar{e}_{{\bar{q}}}{}^{\mu }\partial _{\mu }\), and
$$\begin{aligned} \begin{array}{ll} K_{\mu \nu }=K_{(\mu \nu )}=\partial _{\mu }\Phi \partial _{\nu }\Phi ,\quad&\quad K_{[\mu \nu ]}=0. \end{array} \end{aligned}$$(2.111)In particular, each diagonal component of \(K_{\mu \nu }\) is non-negative, as \(K_{\mu \mu }=(\partial _{\mu }\Phi )^{2}\).
-
Spinor field
Fermionic spinor fields are described by [20]
$$\begin{aligned} L_{\psi }=\bar{\psi }\gamma ^{p}\mathcal{D}_{p}\psi +m_{\scriptscriptstyle {\psi }}\bar{\psi }\psi , \end{aligned}$$(2.112)whereFootnote 6 \(\bar{\psi }=\psi ^{\dagger }A\), \(\,A=A^{\dagger }\), and \((\gamma ^{p})^{\dagger }=-A\gamma ^{p}A^{-1}\).
Under arbitrary variations of the stringy graviton fields and the spinor, the fermionic kinetic term transforms, up to total derivatives (‘\(\simeq \)’), as (c.f. [20, 21])
$$\begin{aligned}&\delta (e^{-2d}\bar{\psi }\gamma ^{A}\mathcal{D}_{A}\psi )\simeq e^{-2d}\delta V_{Ap}{\bar{V}}^{A{\bar{q}}}\,\bar{\psi }\gamma ^{p}\mathcal{D}_{{\bar{q}}}\psi \nonumber \\&\quad +{{\textstyle \frac{1}{4}}}e^{-2d}\delta \Gamma _{ABC}\,\bar{\psi }\gamma ^{A}\gamma ^{BC}\psi \nonumber \\ {}{} & {} \quad +e^{-2d}\left( \delta \bar{\psi }-{{\textstyle \frac{1}{4}}}V_{Ap}\delta V^{A}{}_{q}\bar{\psi }\gamma ^{pq}-2\delta d\,\bar{\psi }\right) \gamma ^{B}\mathcal{D}_{B}\psi \nonumber \\ {}{} & {} \quad -e^{-2d}\mathcal{D}_{B}\bar{\psi }\gamma ^{B}\left( \delta \psi +{{\textstyle \frac{1}{4}}}V_{Ap}\delta V^{A}{}_{q}\gamma ^{pq}\psi \right) . \end{aligned}$$(2.113)In the full-order supersymmetric extensions of DFT [20, 21], the variation of the stringy Christoffel symbols, \(\delta \Gamma _{ABC}\), vanishes automatically, which realizes the ‘1.5 formalism’. However, in the present example, we do not consider any supersymmetry nor quartic fermionic terms. Instead, we proceed, with \(\delta \Gamma _{[ABC]}=0\), to obtain
$$\begin{aligned}&{{\textstyle \frac{1}{4}}}e^{-2d}\delta \Gamma _{ABC}\,\bar{\psi }\gamma ^{A}\gamma ^{BC}\psi ={{\textstyle \frac{1}{2}}}e^{-2d} P^{AB}\delta \Gamma _{ABC}\,\bar{\psi }\gamma ^{C}\psi \nonumber \\&\quad = {{\textstyle \frac{1}{2}}}e^{-2d}\bar{\psi }\gamma ^{A}\psi \left( \mathcal{D}_{p}\delta V_{A}{}^{p}-2\partial _{A}\delta d\right) \nonumber \\&\quad \quad +{{\textstyle \frac{1}{2}}}e^{-2d}\bar{\psi }\gamma ^{p}\psi \,\mathcal{D}_{A}\delta V^{A}{}_{p}\nonumber \\&\quad \simeq e^{-2d}\delta d(\mathcal{D}_{A}\bar{\psi }\gamma ^{A}\psi +\bar{\psi }\gamma ^{A}\mathcal{D}_{A}\psi )\nonumber \\&\quad \quad -e^{-2d}\delta V^{Ap}\left( \mathcal{D}_{(A}\bar{\psi }\gamma _{p)}\psi + \bar{\psi }\gamma _{(A}\mathcal{D}_{p)}\psi \right) , \end{aligned}$$(2.114)and derive the final form of the variation of the fermionic part of the Lagrangian, c.f. an analogous expression in GR (A.9),
$$\begin{aligned}&\delta [e^{-2d}(\bar{\psi }\gamma ^{A}\mathcal{D}_{A}\psi +m_{\scriptscriptstyle {\psi }}\bar{\psi }\psi )]\nonumber \\&\quad \simeq {{\textstyle \frac{1}{2}}}e^{-2d}\delta V_{A}{}^{p}{\bar{V}}^{A{\bar{q}}}(\bar{\psi }\gamma _{p}\mathcal{D}_{{\bar{q}}}\psi -\mathcal{D}_{{\bar{q}}}\bar{\psi }\gamma _{p}\psi )\nonumber \\&\qquad +\,e^{-2d}(\delta \bar{\psi }-\delta d\,\bar{\psi }-{{\textstyle \frac{1}{4}}}V_{A[p}\delta V^{A}{}_{q]}\bar{\psi }\gamma ^{pq})\nonumber \\&\qquad \times (\gamma ^{B}\mathcal{D}_{B}\psi +m_{\scriptscriptstyle {\psi }}\psi )\nonumber \\&\qquad \,-e^{-2d}(\mathcal{D}_{B}\bar{\psi }\gamma ^{B}-m_{\scriptscriptstyle {\psi }}\bar{\psi })(\delta \psi -\delta d\,\psi \nonumber \\&\qquad +{{\textstyle \frac{1}{4}}}V_{A[p}\delta V^{A}{}_{q]}\gamma ^{pq}\psi ). \end{aligned}$$(2.115)This result is quite satisfactory: unlike (2.113), the hermiticity is now manifest, as the first line on the right-hand side is by itself real while the second and the third are hermitian conjugate to each other. Further, as discussed in the general setup (2.73), the infinitesimal local Lorentz rotation of the spinor field by \(V_{A[p}\delta V^{A}{}_{q]}\) can be absorbed into the equation of motion for the matter field through \(\delta \psi ^{\prime }=\delta \psi +{{\textstyle \frac{1}{4}}}V_{A[p}\delta V^{A}{}_{q]}\gamma ^{pq}\psi \). The variation of the DFT dilaton can be also absorbed in the same manner. Comparing (2.75) and (2.115), we obtain
$$\begin{aligned} \begin{array}{ll} K_{p{\bar{q}}}=-{{\textstyle \frac{1}{4}}}(\bar{\psi }\gamma _{p}\mathcal{D}_{{\bar{q}}}\psi -\mathcal{D}_{{\bar{q}}}\bar{\psi }\gamma _{p}\psi ),\qquad&\qquad T_{\scriptscriptstyle {{(0)}}}\equiv 0. \end{array} \end{aligned}$$(2.116)Upon Riemannian backgrounds (2.23), fermions thus provide a nontrivial example of asymmetric \(K_{\mu \nu }\),
$$\begin{aligned} K_{\mu \nu }:= & {} 2e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}\nonumber \\= & {} -\textstyle {\frac{1}{2\sqrt{2}}}(\bar{\psi }\gamma _{\mu }{\bigtriangledown }_{\nu }\psi -{\bigtriangledown }_{\nu }\bar{\psi }\gamma _{\mu }\psi )\ne K_{\nu \mu }. \nonumber \\ \end{aligned}$$(2.117)Finally, if we redefine the field in terms of a spinor density, \(\chi :=e^{-d}\psi \), with weight \(\omega ={{\textstyle \frac{1}{2}}}\), the DFT dilaton decouples from the Lagrangian completely,
$$\begin{aligned} e^{-2d}L_{\psi }= & {} e^{-2d}\left( \bar{\psi }\gamma ^{p}\mathcal{D}_{p}\psi +m_{\scriptscriptstyle {\psi }}\bar{\psi }\psi \right) \nonumber \\= & {} \bar{\chi }\gamma ^{p}\mathcal{D}_{p}\chi +m_{\scriptscriptstyle {\psi }}\bar{\chi }\chi . \end{aligned}$$(2.118)Like fundamental strings, c.f. (2.129), the weightful spinor field \(\chi \) couples only to the DFT vielbeins (or \(g_{\mu \nu }\) and \(B_{\mu \nu }\) for Riemannian backgrounds) [13]. In this case, \(T_{\scriptscriptstyle {{(0)}}}=0\) holds off-shell.
-
Yang–Mills
With the field strength (2.51), the Yang–Mills theory is coupled to Stringy Gravity by [13] (c.f. [48])
$$\begin{aligned} L_{\mathrm{YM}}=\mathrm{Tr}[{\mathbf {F}}_{p{\bar{q}}}{\mathbf {F}}^{p{\bar{q}}}]. \end{aligned}$$(2.119)The corresponding stringy energy–momentum tensor is given, from [23], by
$$\begin{aligned} K_{p{\bar{q}}}= & {} -\mathrm{Tr}[{\mathbf {F}}_{pr}{\mathbf {F}}^{r}{}_{{\bar{q}}}-{\mathbf {F}}_{p{\bar{r}}}{\mathbf {F}}^{{\bar{r}}}{}_{{\bar{q}}}+\mathcal{D}^{M}\left( {{{\mathbf {F}}_{p{\bar{q}}}{\mathbf {A}}_{M}}}\right) ],\nonumber \\ T_{\scriptscriptstyle {{(0)}}}= & {} -2\mathrm{Tr}[{\mathbf {F}}_{p{\bar{q}}}{\mathbf {F}}^{p{\bar{q}}}]. \end{aligned}$$(2.120)When the doubled Yang–Mills gauge potential satisfies the extra condition, \({\mathbf {A}}^{M}\partial _{M}=0\) (2.52), the above expression reduces to, with (2.53),
$$\begin{aligned} K_{p{\bar{q}}}= & {} \mathrm{Tr}[{\mathbf {F}}_{p}{}^{{\bar{r}}}({\mathbf {F}}_{{\bar{r}}{\bar{q}}}+{\mathbf {A}}^{M}{{\bar{\Phi }}}_{M{\bar{r}}{\bar{q}}})\nonumber \\&-({\mathbf {F}}_{pr}+{\mathbf {A}}^{M}\Phi _{Mpr}){\mathbf {F}}^{r}{}_{{\bar{q}}}]\nonumber \\= & {} -\mathrm{Tr}[F_{KL}\mathcal{H}^{LM}F_{MN}V^{K}{}_{p}{\bar{V}}^{N}{}_{{\bar{q}}}]. \end{aligned}$$(2.121) -
Ramond–Ramond sector
The R–R sector of the critical superstring has the kinetic term [21, 46] (c.f. [47, 52, 53])
$$\begin{aligned} L_{\mathrm{RR}}={{\textstyle \frac{1}{2}}}\mathrm{Tr}(\mathcal{F}\bar{\mathcal{F}}), \end{aligned}$$(2.122)where \(\mathcal{F}=\mathcal{D}_{+}\mathcal{C}\) is the R–R field strength given by the nilpotent differential operator \(\mathcal{D}_{+}\) (2.50) acting on the \({\mathbf {Spin}(1,9)}\times {{\mathbf {Spin}}(9,1)}\) bi-spinorial R–R potential \(\mathcal{C}^{\alpha }{}_{\bar{\alpha }}\); \(\bar{\mathcal{F}}=\bar{C}^{-1}\mathcal{F}^{T}C\) is the charge conjugation of \(\mathcal{F}\); and the trace is taken over the \({\mathbf {Spin}(1,9)}\) spinorial indices. This formalism is ‘democratic’, as in [54], and needs to be supplemented by a self-duality relation,
$$\begin{aligned} \gamma ^{{(11)}}\mathcal{F}\equiv \mathcal{F}. \end{aligned}$$(2.123)The R–R sector contributes to the stringy energy–momentum tensor, from (25) of [21] as well as (3.3) of [46], by
$$\begin{aligned} \begin{array}{ll} K_{p{\bar{q}}}=-{{\textstyle \frac{1}{4}}}\mathrm{Tr}(\gamma _{p}\mathcal{F}\bar{\gamma }_{{\bar{q}}}\bar{\mathcal{F}}),\qquad&\qquad T_{\scriptscriptstyle {{(0)}}}\equiv 0. \end{array} \end{aligned}$$(2.124)Upon Riemannian reduction, \(K_{\mu \nu }=2e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}\) is generically asymmetric, \(K_{\mu \nu }\ne K_{\nu \mu }\), which can be verified explicitly after taking the diagonal gauge of the twofold local Lorentz symmetries and then expanding the R–R potential \(\mathcal{C}^{\alpha }{}_{\bar{\beta }}\) in terms of conventional p-form fields [46]. The asymmetry is also consistent with the observation that the \(\mathbf {O}(D,D)\)-covariant nilpotent differential operator \(\mathcal{D}_{+}\) (2.50) reduces to the H-twisted exterior derivative, \(\mathrm{d}_{H}=\mathrm{d}+ H_{\scriptscriptstyle {(3)}}\wedge ~\), such that the B-field contributes to the R–R kinetic term (2.122) in a nontrivial manner.
-
Point particle
We consider the doubled-yet-gauged particle action from [24] and write the corresponding Lagrangian density using a Dirac delta function,
$$\begin{aligned} e^{-2d}L_{\mathrm{particle}}= & {} \int \mathrm{d}\tau ~[\,e^{-1\,}\mathrm{D}_{\tau }y^{A}\mathrm{D}_{\tau }y^{B}\mathcal{H}_{AB}(x)\nonumber \\&-{{\textstyle \frac{1}{4}}}m^{2}e\,]\delta ^{D}\big (x-y(\tau )\big ), \end{aligned}$$(2.125)where \(D_{\tau }y^{M}=\frac{\mathrm{d}~}{\mathrm{d}\tau }{y}^{M}(\tau )-\mathcal{A}^{M}\) is the gauged infinitesimal one-form (2.12). Integrating the above over a section, \(\int _{\Sigma }e^{-2d}L_{\mathrm{particle}}\), one can recover precisely the action in [24]. Note that in Stringy Gravity, the Dirac delta function itself should satisfy the section condition and meet the defining property
$$\begin{aligned} \displaystyle {\int _{\Sigma }\Phi (x)\delta ^{D}(x-y)=\Phi (y).} \end{aligned}$$(2.126)It follows straightforwardly that
$$\begin{aligned} K_{p{\bar{q}}}= & {} -\displaystyle {\int \mathrm{d}\tau }~2e^{-1\,}(\mathrm{D}_{\tau }y)_{p}(\mathrm{D}_{\tau }y)_{{\bar{q}}}\,e^{2d(x)}\delta ^{D}\big (x-y(\tau )\big ),\nonumber \\&T_{\scriptscriptstyle {{(0)}}}=0, \end{aligned}$$(2.127)where, naturally, \((\mathrm{D}_{\tau }y)_{p}=\mathrm{D}_{\tau }y^{A}V_{Ap}\) and \(\,(\mathrm{D}_{\tau }y)_{{\bar{q}}}=\mathrm{D}_{\tau }y^{A}{\bar{V}}_{A{\bar{q}}}\).
Upon Riemannian backgrounds (2.23), (2.25), with \({\tilde{\partial }^{\mu }\equiv 0}\) and the on-shell value of the gauge connection, \(\mathcal{A}^{M}=(A_{\mu },0)\equiv (\frac{\mathrm{d}~}{\mathrm{d}\tau }\tilde{y}_{\mu }-B_{\mu \nu }\frac{\mathrm{d}~}{\mathrm{d}\tau } y^{\nu },0)\) [24], we have
$$\begin{aligned} K_{\mu \nu }= & {} 2e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}\nonumber \\= & {} {\displaystyle {\int \mathrm{d}\tau }}~2e^{-1\,}g_{\mu \rho } g_{\nu \sigma }\frac{\mathrm{d}y^{\rho }}{\mathrm{d}\tau }\frac{\mathrm{d}y^{\sigma }}{\mathrm{d}\tau }\,\frac{\delta ^{D}\big (x-y(\tau )\big )e^{2\phi }}{\sqrt{-g}},\nonumber \\ \end{aligned}$$(2.128)which is symmetric, \(K_{\mu \nu }=K_{\nu \mu }\), as one may well expect for the point particle. Each diagonal component is non-negative, \(K_{\mu \mu }\ge 0\), as \(\big (g_{\mu \rho }\frac{\mathrm{d}y^{\rho }}{\mathrm{d}\tau }\big )^{2}\ge 0\).
-
String
In a similar fashion, the doubled-yet-gauged bosonic string action [41][40] gives
$$\begin{aligned} e^{-2d}L_{\mathrm{string}}= & {} {\textstyle {\frac{1}{4\pi \alpha ^{\prime }}}}{\displaystyle {\int }}\mathrm{d}^{2}\sigma \left[ -{{\textstyle \frac{1}{2}}}\sqrt{-h}h^{\alpha \beta }\mathrm{D}_{\alpha }y^{A}\mathrm{D}_{\beta }y^{B}\mathcal{H}_{AB}(x)\right. \nonumber \\&\left. -\epsilon ^{\alpha \beta }\mathrm{D}_{\alpha }y^{A}\mathcal{A}_{\beta A}\right] \delta ^{D}\big (x-y(\sigma )\big ), \end{aligned}$$(2.129)and hence
$$\begin{aligned} K_{p{\bar{q}}}= & {} {\textstyle {\frac{1}{4\pi \alpha ^{\prime }}}}{\displaystyle {\int }}\mathrm{d}^{2}\sigma \sqrt{-h}h^{\alpha \beta }(\mathrm{D}_{\alpha }y)_{p}(\mathrm{D}_{\beta }y)_{{\bar{q}}}\,e^{2d(x)}\delta ^{D}\big (x-y(\sigma )\big ),\nonumber \\&T_{\scriptscriptstyle {{(0)}}}=0. \end{aligned}$$(2.130)Upon reduction to Riemannian backgrounds (2.23), (2.25), the on-shell value of the gauge connection is \(\mathcal{A}_{\alpha }^{M}=(A_{\alpha \mu },0)\equiv (\partial _{\alpha }\tilde{y}_{\mu }-B_{\mu \nu }\partial _{\alpha }y^{\nu }+\frac{1}{\sqrt{-h}}\epsilon _{\alpha }{}^{\beta }g_{\mu \nu }\partial _{\beta }y^{\nu },0)\) [40], and we have
$$\begin{aligned} K_{\mu \nu }= & {} 2e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}\nonumber \\= & {} \,-\,{\textstyle {\frac{1}{2\pi \alpha ^{\prime }}}}{\displaystyle {\int }}\mathrm{d}^{2}\sigma ~g_{\mu \rho }g_{\nu \sigma } \bigg (\sqrt{-h}h^{\alpha \beta }\nonumber \\&+\epsilon ^{\alpha \beta }\bigg )\partial _{\alpha }y^{\rho }\partial _{\beta }y^{\sigma } \,\frac{\delta ^{D}\big (x-y(\tau )\big )e^{2\phi }}{\sqrt{-g}}, \end{aligned}$$(2.131)which is generically asymmetric, \(K_{\mu \nu }\ne K_{\nu \mu }\), due to the B-field. It is easy to see in lightcone gauge that the diagonal components of \(K_{\mu \nu }\), or \(g_{\mu \rho }\partial _{+}y^{\rho }g_{\mu \sigma }\partial _{-}y^{\sigma }\), are not necessarily positive.
The above analysis further generalizes to the doubled-yet-gauged Green–Schwarz superstring [22],
$$\begin{aligned} K_{p{\bar{q}}}= & {} {\textstyle {\frac{1}{4\pi \alpha ^{\prime }}}}{\displaystyle {\int }}\mathrm{d}^{2}\sigma \sqrt{-h}h^{\alpha \beta }\Pi _{\alpha p}\Pi _{\beta {\bar{q}}}\,e^{2d(x)}\delta ^{D}\big (x-y(\sigma )\big ),\nonumber \\&T_{\scriptscriptstyle {{(0)}}}=0, \end{aligned}$$(2.132)where \(\Pi _{\alpha }^{M}=\partial _{\alpha }y^{M}-\mathcal{A}_{\alpha }^{M}-i\bar{\theta }\gamma ^{M}\partial _{\alpha }\theta -i\bar{\theta }^{\prime }\bar{\gamma }^{M}\partial _{\alpha }\theta ^{\prime }\) is the supersymmetric extension of \(D_{\alpha }y^{M}\).
Upon Riemannian reduction with \(\Pi _{\alpha }^{M}=(\widetilde{\Pi }_{\alpha \mu },\Pi _{\alpha }^{\nu })\), the on-shell value of the gauge connection \(\mathcal{A}_{\alpha }^{M}\) sets \(\widetilde{\Pi }_{\alpha \mu }-B_{\mu \nu }\Pi _{\alpha }^{\nu }+\frac{1}{\sqrt{-h}}\epsilon _{\alpha }{}^{\beta }g_{\mu \nu }\Pi _{\beta }^{\nu }\equiv 0\) [22], and the corresponding \(K_{\mu \nu }\) is similarly asymmetric,
$$\begin{aligned} K_{\mu \nu }= & {} 2e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}=\,-\,{\textstyle {\frac{1}{2\pi \alpha ^{\prime }}}}{\displaystyle {\int }}\mathrm{d}^{2}\sigma ~g_{\mu \rho }g_{\nu \sigma } \bigg (\sqrt{-h}h^{\alpha \beta }\nonumber \\&+\epsilon ^{\alpha \beta }\bigg )\Pi _{\alpha }^{\rho }\Pi _{\beta }^{\sigma } \,\frac{\delta ^{D}\big (x-y(\tau )\big )e^{2\phi }}{\sqrt{-g}}. \end{aligned}$$(2.133)The asymmetry, \(K_{\mu \nu }\ne K_{\nu \mu }\), is a genuine stringy property.
3 Further-generalized Lie derivative, \({{\widetilde{\mathcal{L}}}}_{\xi }\)
In analogy with GR, the notion of isometries in Stringy Gravity can be naturally addressed through the generalized Lie derivative (2.6), which can also, from (2.37), be expressed using DFT-covariant derivatives (2.33), leading to the DFT-Killing equations (2.90) [23],
where the final equalities with ‘\(\,!\,\)’ hold only in the case of an isometry. However, in the vielbein formulation of Stringy Gravity this result needs to be further generalized, as one should be able to construct Killing equations for the DFT vielbeins.
Using \(V^{A}{}_{p}{\bar{V}}^{B}{}_{{\bar{q}}\,}{\hat{\mathcal{L}}}_{\xi }{\bar{P}}_{AB}=-V^{A}{}_{p}{\bar{V}}^{B}{}_{{\bar{q}}\,}{\hat{\mathcal{L}}}_{\xi }P_{AB}=2\mathcal{D}_{[p}\xi _{{\bar{q}}]}\) and the fact that the DFT vielbeins are covariantly constant, \(\mathcal{D}_{A}V_{Bp}=\mathcal{D}_{A}{\bar{V}}_{B{\bar{p}}}=0\) (2.39), their generalized Lie derivatives can be related to the generalized Lie derivatives of the projectors,
These expressions are quite instructive, as we can arrange them as
Motivated by the expressions of the left-hand sides above, we propose to generalize the generalized Lie derivative one step further by constructing a further-generalized Lie derivative, \({{\widetilde{\mathcal{L}}}}_{\xi }\), which can act on an arbitrary tensor density carrying \(\mathbf {O}(D,D)\) and \({\mathbf {Spin}(1,D{-1})}\times {{\mathbf {Spin}}(D{-1},1)}\) indicesFootnote 7 as
In short, the further-generalized Lie derivative comprises the original generalized Lie derivative and additional infinitesimal local Lorentz rotations given by the terms
such that, for example,
The further-generalization is also equivalent to replacing the ordinary derivatives in the original generalized Lie derivative by master derivatives, \({\hat{\mathcal{L}}}_{\xi }^{\partial }\rightarrow {\hat{\mathcal{L}}}_{\xi }^{\mathcal{D}}\), and adding the local Lorentz rotations, \(2\mathcal{D}_{[p}\xi _{q]}\) and \(2\mathcal{D}_{[{\bar{p}}}\xi _{{\bar{q}}]}\).
It is then crucial to note that the further-generalized Lie derivative is completely covariant for both the twofold local Lorentz symmetries and the doubled-yet-gauged diffeomorphisms, as follows. The local Lorentz covariance is guaranteed by the use of the master derivatives everywhere in the definition (3.4). The diffeomorphism covariance also holds, since the original generalized Lie derivative and the additional local Lorentz rotations (3.5) are separately diffeomorphism covariant, from (2.10) and (2.48). For example, the further-generalized Lie derivative acting on a \({\mathbf {Spin}(1,D{-1})}\) spinor field, \(\psi ^{\alpha }\), reads
As expected, or directly seen from (2.49), this expression is completely covariant under both the local Lorentz and the doubled-yet-gauged diffeomorphism transformations. It is advantageous to use \({{\widetilde{\mathcal{L}}}}_{\xi }\) because of its local Lorentz covariance; whereas, in contrast, \({\hat{\mathcal{L}}}_{\xi }\) is not locally Lorentz covariant.
The isometry of the DFT vielbeins is then characterized by the vanishing of their further-generalized Lie derivatives, which is then, with (2.17), (3.1), (3.3), equivalent to nothing but the isometry of the projectors, as
Moreover, gamma and charge conjugation matrices, \((\gamma ^{p})^{\alpha }{}_{\beta }\), \((\bar{\gamma }^{{\bar{p}}})^{\bar{\alpha }}{}_{\bar{\beta }}\), \(C_{\alpha \beta }\), \(\bar{C}_{\bar{\alpha }\bar{\beta }}\), are all compatible with \({{\widetilde{\mathcal{L}}}}_{\xi }\),
The further-generalized Lie derivative is closed by the C-bracket (2.8) and twofold local Lorentz rotations,
of which the two infinitesimal local Lorentz rotation parameters are specified by \(\zeta ^{M}\) and \(\,\xi ^{M}\) as
The closure essentially boils down toFootnote 8
4 Regular spherical solution to Einstein double field equations
In this section we derive the most general, spherically symmetric, asymptotically flat, static, Riemannian, regular solution to the \({D=4}\) Einstein Double Field Equations. Hereafter, we fix the section as \({\tilde{\partial }^{\mu }\equiv 0}\), adopt spherical coordinates, \(\{t,r,\vartheta ,\varphi \}\), and focus on the Riemannian parametrizations (2.22)–(2.25). We shall encounter various parameters and variables, as listed in Table 1.
4.1 Most general \({D=4}\) spherical ansatz
The spherical symmetry in \({D=4}\) Stringy Gravity is characterized by three Killing vectors, \(\xi ^{N}_{a}\), \(a=1,2,3\), which form an \(\mathbf {so}(3)\) algebra through the \(\mathbf {C}\)-bracket,
With \({\tilde{\partial }^{\mu }\equiv 0}\), the \(\mathbf {so}(3)\) Killing vectors, \(\xi ^{N}_{a}=(\tilde{\xi }_{a\mu },\xi _{a}^{\nu })\), decompose explicitly into \(\tilde{\xi }_{a}=\tilde{\xi }_{a\mu }\mathrm{d}x^{\mu }\) and \(\xi _{a}=\xi _{a}^{\nu }\partial _{\nu }\) [24],
where h is constant and B(r) is an arbitrary function of the radius. The three of \(\xi ^{\mu }_{a}\partial _{\mu }\)’s are the standard (undoubled) \(\mathbf {so}(3)\) angular momentum operators. In terms of the further-generalized Lie derivative, the spherical symmetry of the stringy graviton fields implies
such that the DFT-Killing equations (3.1) are satisfied,
On Riemannian backgrounds (2.22), (2.23), (2.25), the above DFT-Killing equations reduce to
In addition to the spherical symmetry we also require the static condition, such that all the fields are time-independent, \(\partial _{t}\equiv 0\). By utilizing ordinary diffeomorphisms we can set \(g_{tr}\equiv 0\) [26], and hence without loss of generality we can put the Riemannian metric into the diagonal form [24]
where \(\mathrm{d}\Omega ^{2}=\mathrm{d}\vartheta ^{2}+\sin ^{2}\vartheta \mathrm{d}\varphi ^{2}\) and \(B_{\scriptscriptstyle {(2)}}={{\textstyle \frac{1}{2}}}B_{\mu \nu }\mathrm{d}x^{\mu }\wedge \mathrm{d}x^{\nu }\). This ansatz solves the spherical DFT-Killing equations, or (4.5), with four unknown radial functions, A(r), B(r), C(r), \(\phi (r)\), and one free constant, h. It differs slightly from the rather well known ansatz in GR (A.29), but accords with the analytic solution in [24]. The H-flux then corresponds to the most general spherically symmetric three-form,Footnote 9
The above ansatz reduces to the flat Minkowskian spacetime if and only if \(A=1\), \(C=r^{2}\), \(B=\phi =h=0\).
It is worth expanding the DFT integral measure, and its integration over \(0\le \vartheta <\pi \) and \(0\le \varphi <2\pi \), on the Riemannian background,
where R denotes the so-called ‘areal radius’,
We further let the energy–momentum tensor, i.e. matter, be spherically symmetric,
which, with (2.74) and (4.3), decomposes into
The latter implies that \(T_{\scriptscriptstyle {{(0)}}}(r)\) is another radial function, while the former gives, using the convention \(K_{p{\bar{q}}}={{\textstyle \frac{1}{2}}}e_{p}{}^{\mu }\bar{e}_{{\bar{q}}}{}^{\nu }K_{\mu \nu }\) (2.98),
which follows from the generic expression of the further-generalized Lie derivative acting on \(K_{p{\bar{q}}}\),
together with the isometry condition (4.5).
Combining these results, we arrive at the final form of \(K_{\mu \nu }\),
such that there are six radial functions, \(K_{tt}(r)\), \(K_{rr}(r)\), \(K_{\vartheta \vartheta }(r)\), D(r), E(r) and F(r), with
In particular, it includes anti-symmetric components which induce a two-form,
This is a novel feature of Stringy Gravity which is not present in GR. For later use, it is worthwhile to note, from (2.92), (2.101), that
and
both of which depend on the radius, r, only.
4.2 Solving the Einstein double field equations
Having prepared the most general spherically symmetric static ansatz, (4.6), (4.14), we now proceed to solve the Einstein double field equations (2.102), (2.103), (2.104). Subtracting the ‘trace’ of (2.102) from (2.104) and employing the differential form notation of (4.7) and (4.16), we focus on the three equivalent equations
We will assume that the stringy energy–momentum tensor is nontrivial only up to a finite radius, \(r_{\mathrm{c}}\), and thus vanishes outside this radius:
That is to say, matter is localized only up to the finite ‘cutoff’ radius, \(r_{\mathrm{c}}\), in a spherically symmetric manner. We emphasize that we never force the H-flux nor the gradient of the string dilaton to be trivial outside a finite radius: this would have been the case if we had viewed them as extra matter, but in the current framework of Stringy Gravity, they are part of the stringy graviton fields, on the same footing as the Riemannian metric, \(g_{\mu \nu }\). Their profiles are dictated by the Einstein Double Field Equations only.
The strict localization of the matter (4.22) motivates us to restrict spacetime to be asymptotically ‘flat’ (Minkowskian) at infinity, by imposing the following boundary conditions [24],
The vacuum expectation value of the string dilaton at infinity, or \(\displaystyle {\lim \nolimits _{r\rightarrow \infty }{e^{-2\phi } =1}}\), is our conventional normalization, as we have the Newton constant, G, at our disposal as a separate free parameter in the master action of Stringy Gravity coupled to matter (2.70). The conditions of (4.22) and (4.23) should enable us to recover the previously acquired, most general, spherically symmetric, asymptotically flat, static vacuum solution to \({D=4}\) Stringy Gravity [24] (c.f. [25]) outside the cutoff radius, \(r\ge r_{\mathrm{c}}\).
In addition, we postulate that matter and hence the spacetime geometry are ‘regular’ and ‘non-singular’ at the origin, \({r=0}\). We require
of which the first is a natural condition for the consistency of the spherical coordinate system at the origin (4.6). The second and third can then be satisfied easily as long as \(A^{\prime }\) and \(\phi ^{\prime }\) are finite at \({r=0}\). Note also that the areal radius, \(R=e^{\phi }\sqrt{C/A}\) (4.9), vanishes at the origin.
All the nontrivial (Riemannian) Christoffel symbols of the metric ansatz (4.6) are, exhaustively [24],
From the off-shell conservation of the stringy Einstein tensor, the three equations (4.19), (4.20), (4.21) must imply the on-shell conservation of the stringy energy–momentum tensor as in (2.96) and (2.97). For the present spherical and static ansatz, the nontrivial components of (2.96) come from ‘\({\nu =t}\)’ and ‘\({\nu =r}\)’ only. They are, respectively,
and
On the other hand, for (2.97), there appears only one nontrivial relation from the choice of ‘\({\nu =t}\)’,
We will confirm that these relations are indeed satisfied automatically by the three Eqs. (4.19), (4.20), (4.21) which reduce, with the Christoffel symbols (4.25), as follows. Firstly, the scalar equation (4.19) becomes
The Ricci curvature, \(R_{\mu \nu }\), and the two derivatives of the string dilaton, \({\bigtriangledown }_{\mu }\partial _{\nu }\phi \), are automatically diagonal, such that the tensorial equation (4.20) is almost diagonal,

with one exception, an off-diagonal component,
The last equation for the H-flux (4.21) becomes
which gives
The former result of (4.33) satisfies the conservation relation (4.28) trivially, while the latter combined with (4.31) implies the conservation relation (4.26). Integrating the latter, we get
where we set
and q is a constant of integration. From our assumption (4.22), when \(r\ge r_{\mathrm{c}}\), both F(r) and \(\mathcal{V}(r)\) vanish, and consequently \(e^{-4\phi }A^{2}BC^{-1}\) assumes the constant value, q. Now, substituting (4.34) into the second formula in (4.30), we get
The infinite radius limit of this expression implies, with the conditions of (4.22) and (4.23), that actually q must be trivial: \(q=0\). Therefore, from (4.34), we are able to fix B(r) and hence \(H_{r\vartheta \varphi }\),
which vanish when \(r\ge r_{\mathrm{c}}\), in agreement with the known vacuum solution [24].
The remaining Einstein Double Field Equations (4.29), (4.30), (4.31) reduce, with \({{\displaystyle {\int _{\vartheta }\int _{\varphi } e^{-2d\,}}}}\equiv 4\pi e^{2\phi }A^{-1}C\) from (4.8), to
The first Eq. (4.38) indicates that h is a proportionality constant relating \(\mathcal{V}=e^{-4\phi }A^{2}BC^{-1}\) to \(K_{(tr)}C\). On the other hand, the radial derivative of the entire expression in the last formula (4.42), after substitution of (4.37), (4.39), (4.40), and (4.41), implies the remaining conservation relation (4.27):
This provides a consistency check for the Eqs. (4.39)–(4.42), and completes our concrete verification that all the energy–momentum conservation laws indeed follow from the Einstein double field equations.
In order to solve or integrate the second and the third equations, (4.39), (4.40), we prepare the following definitions,
which all vanish at the origin, \(r=0\). Further, when \(r\ge r_{\mathrm{c}}\), the un-hatted functions, \(\mathcal{W}(r)\), \(\mathcal{X}(r)\), \(\mathcal{Y}(r)\), become constant – for example, \(\mathcal{X}(r)=\mathcal{X}(r_{\mathrm{c}})\equiv \mathcal{X}_{\mathrm{c}}\) for \(r\ge r_{\mathrm{c}}\). Consequently, the hatted functions become linear in the outside region,
Integrating (4.39) twice, we can solve for C(r). There are two constants of integration which we fix by imposing the boundary conditions at the origin: firstly we set \({C(0)=0}\) directly from (4.24) and secondly, with \(\phi _{\scriptscriptstyle {0}}\equiv \phi (0)\), we fix \(C^{\prime }(0)=\pm he^{-2\phi _{\scriptscriptstyle {0}}}\) from the consideration of the small r limit of (4.42). We get
Outside the matter this reduces to a quadratic equation,
where we set two constants,
Similarly, (4.40) gives
for which the trivial constant of integration (zero) has been chosen to meet the boundary condition at the origin (4.24). Eq.(4.49) can be further integrated to determine A(r) with the boundary condition, this time at infinity (4.23),
Away from the matter, with (4.47), this reduces to a closed form,
where we have introduced another constant,
such that outside the matter,
For A(r) to be real and positive, it is necessary to restrict the range of r. Since \(\alpha +\beta \) is positive semi-definite from (4.48), we are lead to require the cutoff radius to be greater than \(\alpha \), such that
However, note that the signs of \(\alpha \) and \(\beta \) are not yet fixed: in the next Sect. 4.3 we shall assume some energy conditions which will ensure both \(\alpha \) and \(\beta \) are positive.
We now turn to the last differential equation (4.42). Upon substitution of (4.47) and (4.49), it takes the form
which, from (4.51), (4.52), reduces outside the matter to
This new constant, b, meets
Since the left-hand side of (4.56) is positive, b should be real, and from (4.48), \(\alpha +\beta \) is positive since
Therefore, outside the matter we have
such that
of which both sides can be integrated to give
We can determine the constant of integration in (4.61) from the boundary condition at infinity (4.23),
to obtain the profile of the string dilaton outside the matter,
where b can be either positive or negative, and \(\gamma _{+}\), \(\gamma _{-}\) denote two positive semi-definite constants,
For the sake of reality, we requireFootnote 10
This completes our derivation of the spherically symmetric, static, regular solution to \({D=4}\) Stringy Gravity with a localized stringy matter distribution.
We conclude this subsection by summarizing and analyzing our results.
-
Outside the cutoff radius, \(r\ge r_{\mathrm{c}}\), we recover the spherically symmetric static vacuum solution [24]:
 (4.66)
(4.66) -
Moreover, the constants, \(\alpha ,\beta ,a,b,h\), are now all determined by the stringy energy–momentum tensor of the matter localized inside the cutoff radius: from (4.48), (4.52), (4.57),
$$\begin{aligned} \alpha= & {} {{\textstyle \frac{1}{2}}}\left[ \sqrt{\left( \mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}}\right) ^{2}+4\widetilde{\mathcal{Z}}_{\mathrm{c}}\,}\,-\left( \mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}}\right) \right] ,\nonumber \\ \beta= & {} {{\textstyle \frac{1}{2}}}\left[ \sqrt{(\mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}})^{2}+4\widetilde{\mathcal{Z}}_{\mathrm{c}}\,}\,+\left( \mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}}\right) \right] ,\nonumber \\ a= & {} \displaystyle {\int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi }~e^{-2d}\left[ {\frac{1}{4\pi }}H_{r\vartheta \varphi }H^{r\vartheta \varphi }\right. \nonumber \\&\left. +2 G\left( K_{r}{}^{r}+K_{\vartheta }{}^{\vartheta }+K_{\varphi }{}^{\varphi }-K_{t}{}^{t}-T_{\scriptscriptstyle {{(0)}}}\right) \right] ,\nonumber \\ b^{2}= & {} \left( \mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}}\right) ^{2}+4\widetilde{\mathcal{Z}}_{\mathrm{c}}\,-a^{2},\nonumber \\ \displaystyle h= & {} \frac{K_{tr}C}{\displaystyle {\int _{r}^{\infty }\mathrm{d}r~e^{-2d}K^{\vartheta \varphi }}}, \end{aligned}$$(4.67)where, with (4.44),
$$\begin{aligned} \mathcal{Z}(r):= & {} \displaystyle {\int _{0}^{r}\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi }~e^{-2d}\left[ {\frac{1}{4\pi }}H_{r\vartheta \varphi }H^{r\vartheta \varphi }\right. \nonumber \\&\left. +4 G\left( K_{r}{}^{r}+K_{\vartheta }{}^{\vartheta }-T_{\scriptscriptstyle {{(0)}}}\right) \right] =\mathcal{W}(r)+4\mathcal{X}(r),\nonumber \\ \widetilde{\mathcal{Z}}_{\mathrm{c}}:= & {} \displaystyle {\int _{0}^{r_{\mathrm{c}}}\mathrm{d}r}~[\mathcal{Z}_{\mathrm{c}}-\mathcal{Z}(r)]. \end{aligned}$$(4.68)As before, the subscript index, \(\mathrm{c}\), denotes the position at \(r=r_{\mathrm{c}}\), such that \(\mathcal{Z}_{\mathrm{c}}=\mathcal{Z}(r_{\mathrm{c}})\).
-
Some further comments are in order.
-
There are two classes of solutions: \(b=\sqrt{(\alpha +\beta )^{2}-a^{2}} \ge 0~\) or \(~b=-\sqrt{(\alpha +\beta )^{2}-a^{2}}<0\).
-
Direct computation from (4.63) shows
$$\begin{aligned} 2\phi ^{\prime }C e^{2\phi }= & {} b\left[ \gamma _{+}\left( \textstyle {\frac{r-\alpha }{r+\beta }}\right) ^{\frac{b}{\sqrt{a^{2}+b^{2}}}}-\gamma _{-}\left( \textstyle {\frac{r+\beta }{r-\alpha }}\right) ^{\frac{b}{\sqrt{a^{2}+b^{2}}}}\right] \nonumber \\= & {} \widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}b\sqrt{e^{4\phi }-h^{2}/b^{2}}, \end{aligned}$$(4.69)where we define a sign factor,
$$\begin{aligned} \widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}:=\left\{ \begin{array}{lllll} +1\quad &{}\quad \mathrm{if}\quad &{} b>0&{} \mathrm{and} &{}r\ge r_{\scriptscriptstyle {\mathbf {\phi }}}\\ -1\quad &{}\quad \mathrm{if}\quad &{} b>0&{}\mathrm{and} &{} r_{\scriptscriptstyle {\mathbf {\phi }}}>r\ge \alpha \\ +1\quad &{}\quad \mathrm{if}\quad &{}b<0&{} \mathrm{and} &{} r\ge \alpha , \end{array}\right. \end{aligned}$$(4.70)with the zero of \(\phi ^{\prime }\) given by
$$\begin{aligned} \displaystyle r_{\scriptscriptstyle {\mathbf {\phi }}}:= & {} \frac{\,\alpha \,+\,\beta \left( \frac{\gamma _{-}}{\gamma _{+}}\right) ^{\frac{\sqrt{a^{2}+b^{2}}}{2b}}}{1-\left( \frac{\gamma _{-}}{\gamma _{+}}\right) ^{\frac{\sqrt{a^{2}+b^{2}}}{2b}}},\quad \quad \phi ^{\prime }(r_{\scriptscriptstyle {\mathbf {\phi }}})=0,\nonumber \\ \phi (r_{\scriptscriptstyle {\mathbf {\phi }}})= & {} {{\textstyle \frac{1}{2}}}\ln \left| h/b\right| <0. \end{aligned}$$(4.71)When h is trivial, we have \(\gamma _{-}=0\), \(r_{\scriptscriptstyle {\mathbf {\phi }}}=\alpha \) and hence \(\widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}\) is fixed to be \(+1\). If \(h\ne 0\) and \(b>0\), then \(r_{\scriptscriptstyle {\mathbf {\phi }}}>\alpha \). Otherwise (\(h\ne 0\) and \(b<0\)) we have the opposite, \(r_{\scriptscriptstyle {\mathbf {\phi }}}<\alpha \). In fact, when b is negative, \(r_{\scriptscriptstyle {\mathbf {\phi }}}\) also becomes negative and thus unphysical. That is to say, for large enough r, i.e. either \(r\ge \alpha \) with negative \({b}\,\) or \(\,{r\ge r_{\scriptscriptstyle {\mathbf {\phi }}}}\) with positive b, the sign of \(\phi ^{\prime }\) coincides with that of b, but when b is positive, \(\phi ^{\prime }\) becomes negative in the finite interval \(\,\alpha \le r<r_{\scriptscriptstyle {\mathbf {\phi }}}\).
-
Since b is real, the following inequality must be met:
$$\begin{aligned} (\mathcal{Z}_{\mathrm{c}}\pm he^{-2\phi _{\scriptscriptstyle {0}}})^{2}+4\widetilde{\mathcal{Z}}_{\mathrm{c}}\,\ge \, a^{2}, \end{aligned}$$(4.72)which imposes a constraint on the stringy energy–momentum tensor through (4.67).
-
From (4.8), outside the matter the integral measure in Stringy Gravity reads
$$\begin{aligned} e^{-2d}= & {} R^{2}\sin \vartheta =\left[ \gamma _{+}\left( \frac{r+\beta }{r-\alpha }\right) ^{\frac{a-b}{\sqrt{a^{2}+b^{2}}}}\right. \nonumber \\&\left. +\gamma _{-}\left( \frac{r+\beta }{r-\alpha }\right) ^{\frac{a+b}{\sqrt{a^{2}+b^{2}}}}\right] \nonumber \\&(r-\alpha )(r+\beta )\sin \vartheta \quad \mathrm{for} \quad r\ge r_{\mathrm{c}}. \end{aligned}$$(4.73) -
With the boundary condition at the origin (4.24), the Einstein double field equations (4.40), (4.41) enable us to evaluate, for arbitrary \(r\ge 0\),
$$\begin{aligned} \begin{array}{lll} &{}&{}2\phi ^{\prime }C+A^{\prime }A^{-1}C =\displaystyle {\int _{0}^{r}\mathrm{d}r~{\frac{\mathrm{d}~}{\mathrm{d}r}}\left( 2\phi ^{\prime }C+A^{\prime }A^{-1}C\right) }\\ &{}&{}\quad =\displaystyle {\int _{0}^{r}\mathrm{d}r~\left( h^{2}e^{-4\phi }C^{-1}- 16\pi GK_{t}{}^{t}e^{2\phi }A^{-1}C \right) }\\ &{}&{}\quad =\displaystyle {\int _{0}^{r}\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi ~e^{-2d}}\\ &{}&{}\qquad \times \displaystyle {\left( \frac{1}{4\pi }\left| H_{t\vartheta \varphi }H^{t\vartheta \varphi }\right| - 4 GK_{t}{}^{t} \right) }, \end{array} \end{aligned}$$(4.74)where \(H_{t\vartheta \varphi }H^{t\vartheta \varphi }=-h^{2}e^{-6\phi }AC^{-2}\).
-
Combining (4.69) and (4.74) with the boundary condition at infinity (4.23), (4.53), we acquire
$$\begin{aligned} \displaystyle a+b\sqrt{1-h^{2}/b^{2}}= & {} \int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi ~e^{-2d}\nonumber \\&\times \left( \frac{1}{4\pi }\left| H_{t\vartheta \varphi }H^{t\vartheta \varphi }\right| - 4 GK_{t}{}^{t} \right) . \nonumber \\ \end{aligned}$$(4.75)We stress that this result is valid irrespective of the sign of b.
-
The constant parameter, h, corresponding to the electric H-flux, is given by the formula (4.67)
$$\begin{aligned} h=K_{tr}(r)C(r)\big /\left[ \displaystyle {\int _{r}^{\infty }\mathrm{d}r~e^{-2d}K^{\vartheta \varphi }}\right] . \end{aligned}$$(4.76)While this is a nontrivial relation, as the right-hand side of the equality must be constant independent of r, it is less informative compared to the integral expressions of a in (4.67) or \(a+b\sqrt{1-h^{2}/b^{2}}\) in (4.75). We expect a fuller understanding of the h parameter will arise if we solve for the time-dependent dynamical Einstein Double Field Equations, allowing h to be time-dependent, \(h\rightarrow h(t)\). In any case, (4.76) implies that if \(K_{tr}\) is nontrivial somewhere in the interior, there must be electric H-flux everywhere, including outside the matter.
-
The small-r radial derivative of the areal radius R (4.9) outside the matter reads, with the sign factor \(\widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}\) (4.70),
$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}r}= & {} e^{2\phi }A^{-1}R^{-1}\bigg [r-\alpha +{{\textstyle \frac{1}{2}}}\sqrt{a^{2}+b^{2}}-{{\textstyle \frac{1}{2}}}a \nonumber \\&+{{\textstyle \frac{1}{2}}}\widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}b\sqrt{1-(h^{2}/b^{2})e^{-4\phi }}\,\bigg ]\quad \mathrm{for} \quad r\ge r_{\mathrm{c}}. \nonumber \\ \end{aligned}$$(4.77) -
From (4.8), (4.17), (4.33), (4.38), the Noether charge (2.92) for a generic Killing vector reads
$$\begin{aligned} \mathcal{Q}[\xi ]= & {} \displaystyle {\int _{\Sigma }}~e^{-2d}T^{t}{}_{A}\xi ^{A}=\displaystyle {\int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi } \nonumber \\&\times \left[ e^{-2d}(K_{t}{}^{t}-{{\textstyle \frac{1}{2}}}T_{\scriptscriptstyle {{(0)}}})\xi ^{t}+\frac{1}{16\pi G}h\mathcal{V}A^{-2}\xi ^{r}\sin \vartheta \right] . \nonumber \\ \end{aligned}$$(4.78)
4.3 Energy conditions
In this subsection we assume that the stringy energy–momentum tensor and the stringy graviton fields satisfy the following three conditions:
- (i):
-
the strong energy condition, with magnetic H-flux,
$$\begin{aligned}&\displaystyle \int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi \,\,\,e^{-2d}\biggl ( -K_{t}{}^{t}+K_{r}{}^{r}+K_{\vartheta }{}^{\vartheta }\nonumber \\&\quad +K_{\varphi }{}^{\varphi }-T_{\scriptscriptstyle {{(0)}}}+\frac{1}{8\pi G}\left| H_{r\vartheta \varphi }H^{r\vartheta \varphi }\right| \biggr )~\ge ~0\,; \end{aligned}$$(4.79) - (ii):
-
the weak energy condition, with electric H-flux,
$$\begin{aligned} \displaystyle {\int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi \,\,\, e^{-2d}\left( -K_{t}{}^{t}+\frac{1}{16\pi G}\left| H_{t\vartheta \varphi }H^{t\vartheta \varphi }\right| \right) ~\ge ~0\,;} \nonumber \\ \end{aligned}$$(4.80) - (iii):
-
the pressure condition, with magnetic H-flux and without integration,
$$\begin{aligned} K_{r}{}^{r}+K_{\vartheta }{}^{\vartheta }-T_{\scriptscriptstyle {{(0)}}}+\frac{1}{16\pi G}\left| H_{r\vartheta \varphi }H^{r\vartheta \varphi }\right| ~\ge ~0. \end{aligned}$$(4.81)
While the nomenclatures are in analogy with those in General Relativity, the precise expression in each inequality, including the H-flux, is what we shall need in our discussion. Since the magnetic H-flux vanishes outside the matter along with the stringy energy–momentum tensor, (4.35), (4.37), the radial integration in the strong energy condition (4.79) is taken effectively from zero to the cutoff radius, i.e. \(\int _{0}^{r_{\mathrm{c}}}\). In contrast, the electric H-flux has a long tail and the weak energy condition genuinely concerns the infinite volume integral.
If the matter comprises point particles only as in (2.125), the above conditions are all clearly met, since \(K_{r}{}^{r}\), \(K_{\vartheta }{}^{\vartheta }\), \(K_{\varphi }{}^{\varphi }\) and \(-K_{t}{}^{t}\) are individually positive semi-definite, while \(T_{\scriptscriptstyle {{(0)}}}\) is trivial. In such cases, not only the integrals but also the integrands themselves are positive semi-definite, which would imply
and similarly for the strong energy density condition. However, for stringy matter, such as fermions (2.112) or fundamental strings (2.129), the diagonal components, \(K_{\mu \mu }\), may not be positive definite, and so the above inequalities appear not to be guaranteed (hence the question mark in (4.82)). If the diagonal components are negative, the positively squared H-fluxes need to compete with them. In fact, while we take the energy and the pressure conditions (4.79), (4.80), (4.81) for granted,Footnote 11 we shall distinguish the energy condition from the energy density condition, and in particular investigate the implications of the relaxation of the latter (4.82).
Obviously, from (4.67), the strong energy condition sets the constant, a, to be positive semi-definite. Similarly, the pressure condition ensures \(\mathcal{Z}(r)\) is a non-decreasing positive function, reaching its maximum value at the cutoff radius, such that \(0\le \mathcal{Z}(r)\le \mathcal{Z}_{\mathrm{c}}\) and \(\mathcal{Z}^{\prime }\ge 0\). Consequently, \(\widetilde{\mathcal{Z}}_{\mathrm{c}}\) is positive semi-definite and thus \(\alpha \) and \(\beta \) are both safely real and positive. In this way, the strong energy and the pressure conditions ensure
Given this positiveness, the string dilaton, \(\phi \), outside the matter (4.63),
diverges to plus infinity when \(r\rightarrow \alpha ^{+}\) and \(h\ne 0\), irrespective of the sign of b. Specifically, if \(b>0\) and \(h\ne 0\), \(\phi \) decreases from \(\infty \) over the finite interval of \(\alpha<r<r_{\scriptscriptstyle {\mathbf {\phi }}}\), crossing the horizontal axis of \({\phi =0}\) at \(r=\frac{\alpha +\beta (\gamma _{-}/\gamma _{+})^{\sqrt{1+a^{2}/b^{2}}}}{1-(\gamma _{-}/\gamma _{+})^{\sqrt{1+a^{2}/b^{2}}}}\), reaches its minimum, \(\phi _{\scriptscriptstyle {\mathrm {min}}}={{\textstyle \frac{1}{2}}}\ln \left| h/b\right| <0\) at \(r=r_{\scriptscriptstyle {\mathbf {\phi }}}\) (4.71), and then increases to converge to zero over the semi-infinite range, \(\,r_{\scriptscriptstyle {\mathbf {\phi }}}<r\le \infty \). On the other hand, when \(b>0\) and \(h=0\), the dilaton \(\phi \) increases monotonically from \(-\infty \) to zero over the whole range, \(\alpha <r\le \infty \), and if \(b<0\), for all h, it is the opposite: \(\phi \) decreases monotonically from \(\infty \) to zero over \(\alpha <r\le \infty \).
Now we turn to the weak energy condition. To see its implications, we consider the circular geodesic motion of a point particle (2.125), which orbits around the central matter with fixed r larger than \(r_{\mathrm{c}}\),
With the nontrivial Christoffel symbols (4.25), the radial ‘\(\lambda =r\)’ component of the geodesic equation, \(\frac{\mathrm{d}^{2}r}{\mathrm{d}\tau ^{2}}+\gamma ^{r}_{tt}\big (\frac{\mathrm{d}t}{\mathrm{d}\tau }\big )^{2}+\gamma ^{r}_{\varphi \varphi }\big (\frac{\mathrm{d}\varphi }{\mathrm{d}\tau }\big )^{2}=0\), determines the angular velocity [24],
Associating this with the centripetal acceleration measured by the areal radius through Newtonian gravity, we define and analyze an effective mass, M(r), as a function of the radius,
From (4.69) and (4.74), we have explicitly, with the sign factor, \(\widehat{\varepsilon }_{\scriptscriptstyle {\mathbf {\phi \,}}}\) (4.70),
where we have set
which is positive definite for sufficiently large r, having the limit,
In fact, for \(r>\alpha \), \(h\ne 0\),Footnote 12 the numerator in (4.89) is positive-definite, while the denominator,
is a monotonically increasing function over \(\alpha <r\le \infty \), taking values from a non-positive number to plus infinity: with (4.69),
If and only if \(ab=0\), we have strictly \(\displaystyle {\lim _{r\rightarrow \alpha }\Omega (r)=0}\). Otherwise, \(\mathcal{I}(r)\) diverges generically for some finite \(r=r_{{\scriptscriptstyle {\Omega }}}>\alpha \), as \(\Omega (r_{{\scriptscriptstyle {\Omega }}})=0\).
We consider taking the large r limit of (4.88), with the boundary condition (4.23), to obtain
While the first equality, or \(GM_{\infty }={{\textstyle \frac{1}{2}}}(a+b\sqrt{1-h^{2}/b^{2}})\), is the confirmation of the known result in [24], the second equality reveals the relationship of the mass, \(M_{\infty }\), to the infinite-volume integral of the stringy energy–momentum tensor and the electric H-flux. The weak energy condition (4.80) then precisely corresponds to the sufficient and necessary condition for the mass to be positive semi-definite, \(M_{\infty }\ge 0\).
In fact, the mass, \(M_{\infty }\), appears in the expansion of the metric, specifically the temporal component, \(g_{tt}\), in the inverse of the areal radius,Footnote 13
and similarly,
Thus, effectively, the circular geodesic becomes Keplerian for large enough R: that is to say, Stringy Gravity tends to agree with GR at long distances (\({R>>GM_{\infty }}\)). However, if M(r) is ever negative for some finite r, it means that the gravitational “force” a la (4.87) is repulsive! With (4.92), if \(M(r_{{\scriptscriptstyle {\Omega }}})\) diverges to plus infinity, the gravitational force is attractive and singular at \({r=r_{{\scriptscriptstyle {\Omega }}}}\). On the other hand, if \(M(r_{{\scriptscriptstyle {\Omega }}})=-\infty \), there appears an infinite ‘wall’ of repulsive force at the surface of \({r=r_{{\scriptscriptstyle {\Omega }}}}\).
We proceed to investigate if M(r) can be negative. For this, we look for the zero of M(r), denoted by \(r_{{\scriptscriptstyle {M}}}\), which from (4.54) should be greater than \(\alpha \),
Firstly, for the special case of \(h=0\) (and thus \({\gamma _{+}=1}\), \({\gamma _{-}=0}\)), we have outside the matter,
This does not admit any zero which is greater than \(r_{\mathrm{c}}\). In particular, if \(b=0\), we get \(2GM=a\) constant. Henceforth we focus on nontrivial \(h\ne 0\). In this case, if and only if \(\,\left| b\right| \ge \left| a\right| \), \(\,M(r)\) admits a zero, \(r_{{\scriptscriptstyle {M}}}\), which is uniquely fixed a priori from the first equality of (4.88): with \({a=\left| a\right| }\) (4.83),
Clearly in the case of \(\left| b\right| \ge \left| a\right| \) (and \({h}\ne 0\)), \(r_{{\scriptscriptstyle {M}}}\) is real valued and thus can be physical. The second equality of (4.88) implies that the zero of M(r) necessarily meets
such that, from (4.70), when \(b>0\), the zero must be between \(\alpha \) and \(r_{\scriptscriptstyle {\mathbf {\phi }}}\),
Indeed, this can be verified directly as follows. Provided \(\left| b\right| >\left| a\right| \), the root is greater than \(\alpha \), since
and \(2GM_{\infty }\) is positive definite, irrespective of the sign of b, owing to the weak energy condition (4.80). Further, with \(b>0\), we have from (4.71),
which is positive since \(0<\frac{\gamma _{-}(\left| b\right| -\left| a\right| )}{\gamma _{+}(\left| b\right| +\left| a\right| )}<\frac{\gamma _{-}}{\gamma _{+}}<1\). This completes our direct verification of (4.100).
In order to see the behaviour of M(r), or its sign change around the zero, \({r=r_{{\scriptscriptstyle {M}}}}\), we need to analyze \(\mathcal{I}(r)\). As mentioned earlier, the numerator is (harmlessly) positive. Therefore, we focus on the denominator, \(\Omega (r)\) (4.91). At \(r=r_{{\scriptscriptstyle {M}}}\), with \(\left| b\right| \ge \left| a\right| \) it reads
Clearly, \(\Omega (r_{{\scriptscriptstyle {M}}})\) is negative when \(\left| b\right| =\left| a\right| \), as it reads \(\Omega (r_{{\scriptscriptstyle {M}}})=(\frac{1}{\sqrt{2}}-1)\left| a\right| \). On the other hand, when \(\left| b\right| \) is sufficiently large it becomes positive, for example, \(\left| b\right| \ge \sqrt{3}\left| a\right| \). In order to locate the exact critical value of \(\left| b\right| \), we let \(\left| b\right| =\left| a\right| \sinh \upsilon \). For \(\left| b\right| \ge \left| a\right| \), we restrict the range of the parameter \(\upsilon \ge \ln (1+\sqrt{2})\). Now, the precise critical value of \(\upsilon \) for which \(\Omega (r_{{\scriptscriptstyle {M}}})\) (4.103) is trivial is determined by the following relation:
The left-hand side of the first equality, viewed as a function of \(\upsilon \), increases monotonically from zero to infinity over the range \(\ln (1+\sqrt{2})\le \upsilon \le \ln (2+\sqrt{3})\), corresponding to \(1\le \sinh \upsilon \le \sqrt{3}\). For the right-hand side, we treat the two cases, \(b>\left| a\right| \) and \(b<-\left| a\right| \), separately. When \(b>\left| a\right| \), the far right-hand side increases from zero to a finite positive value, \(1/\gamma _{-}+\sqrt{3}(\gamma _{+}/\gamma _{-}-1)>0\). Hence there must be one critical value of \(\upsilon \), say \(\upsilon _{\mathrm{c}}\), that meets the above equality. For the opposite case of \(b<-\left| a\right| \), since the right-hand side or \(M_{\infty }\) should be positive, the range of \(\sinh \upsilon \) is further restricted to \(1\le \sinh \upsilon \le \min \big [\sqrt{3},(\gamma _{+}-\gamma _{-})^{-1}\big ]\). In either case, \(\sqrt{3}\ge \frac{1}{\gamma _{+}-\gamma _{-}}\) or \(\sqrt{3}<\frac{1}{\gamma _{+}-\gamma _{-}}\), it is easy to see, from the boundary values, that there must also exist \(\upsilon _{\mathrm{c}}\) satisfying the above equality for \(b<-\left| a\right| \).
Lastly, when \(\left| b\right| =\left| a\right| \sinh \upsilon _{\mathrm{c}}\), we have \(r_{{\scriptscriptstyle {M}}}=r_{{\scriptscriptstyle {\Omega }}}\) and \(GM(r_{{\scriptscriptstyle {M}}})\) turns out be positive-finite:
In this case, it diverges at \({r=\alpha \,}\) as \(\displaystyle {\lim _{\,~r\rightarrow \alpha ^{+}}GM(r)=\infty }\).
To summarize, there exists a critical value of \(\left| b\right| \) given by \(\left| a\right| \sinh \upsilon _{\mathrm{c}}\) which is located between \(\left| a\right| \) and \(\sqrt{3}\left| a\right| \), such that if \(\left| b\right| >\left| a\right| \sinh \upsilon _{\mathrm{c}}\), we have \(r_{{\scriptscriptstyle {\Omega }}}<r_{{\scriptscriptstyle {M}}}\) and hence, crossing \({r=r_{{\scriptscriptstyle {M}}}}\) from outside (\({r>r_{{\scriptscriptstyle {M}}}}\)) to inside (\({r<r_{{\scriptscriptstyle {M}}}}\)), the gravity changes from being attractive, \(M(r)>0\), to repulsive, \(M(r)<0\). Further deep inside at \({r=r_{{\scriptscriptstyle {\Omega }}}}\), there is an infinite repulsive wall. On the other hand, if \(\left| b\right| <\left| a\right| \sinh \upsilon _{\mathrm{c}}\), we have \(r_{{\scriptscriptstyle {M}}}<r_{{\scriptscriptstyle {\Omega }}}\), such that upon approaching from infinity towards the center, the effective mass, M(r), or the attractive gravitational force, increases and eventually diverges at \(r=r_{{\scriptscriptstyle {\Omega }}}\). In the special case of \(\left| b\right| =\left| a\right| \sinh \upsilon _{\mathrm{c}}\), M(r) is positive-definite for \(r\ge r_{\mathrm{c}}>\alpha \).
In either the case of \(\left| b\right| >\left| a\right| \sinh \upsilon _{\mathrm{c}}\) or \(\left| b\right| <\left| a\right| \sinh \upsilon _{\mathrm{c}}\), in order to avoid (crossing) the singularity at \(r_{{\scriptscriptstyle {\Omega }}}\), it seems physically reasonable to have
Specifically when \(\left| b\right| \) is large enough, or \(\left| b\right| >\left| a\right| \sinh \upsilon _{\mathrm{c}}\), and thus there is an infinite repulsive wall at \({r=r_{{\scriptscriptstyle {\Omega }}}}\), the above assumption (4.106) appears even more physically natural, as no falling body can penetrate the wall. In contrast, if b is small such that \(\left| b\right| <\left| a\right| \sinh \upsilon _{\mathrm{c}}\), it may be hard to maintain the above condition since the gravitational attraction may become too strong. For this reason, it appears necessary to postulate the large \(\left| b\right| \) condition, i.e.
along with the strong energy (4.79), weak energy (4.80), and pressure (4.81) conditions. The allowed parameter region is shown in Fig. 1.
The parameter space for \((h/\left| b\right| ,\left| a\right| /b)\). In the gray region we have \(r_{{\scriptscriptstyle {M}}}>r_{{\scriptscriptstyle {\Omega }}}\,\), whereas this is not satisfied in the outer white region. The black region corresponds to violation of the weak energy condition and is thus excluded
5 Conclusion
In this work we have proposed that Double Field Theory is Stringy Gravity, i.e. the upgrade of General Relativity which is in accordance with the symmetries of string theory. To this end we developed a definition for the stringy energy–momentum tensor and presented the Einstein Double Field Equations. As an example, we focused on \({D=4}\) regular solutions. Our main results are summarized below with comments.
- \(*\) :
-
For a generic action of Stringy Gravity (2.70),
$$\begin{aligned} \displaystyle {\int _{\Sigma }e^{-2d}\Big [\,\textstyle {\frac{1}{16\pi G}}S_{\scriptscriptstyle {{(0)}}}+L_{\mathrm{matter}}\,\Big ],} \end{aligned}$$(5.1)the stringy energy–momentum tensor is defined by (2.85),
$$\begin{aligned} T_{AB}:=4V_{[A}{}^{p}{\bar{V}}_{B]}{}^{{\bar{q}}}K_{p{\bar{q}}}-{{\textstyle \frac{1}{2}}}\mathcal{J}_{AB}T_{\scriptscriptstyle {{(0)}}}, \end{aligned}$$(5.2)which contains \({D^{2}+1}\) components (2.74),
$$\begin{aligned} K_{p{\bar{q}}}:= & {} \displaystyle {\frac{1}{2} \left( V_{Ap}\frac{\delta L_{\mathrm{matter}}}{\delta {\bar{V}}_{A}{}^{{\bar{q}}}}-{\bar{V}}_{A{\bar{q}}}\frac{\delta L_{\mathrm{matter}}}{\delta V_{A}{}^{p}}\right) ,}\nonumber \\ T_{\scriptscriptstyle {{(0)}}}:= & {} e^{2d}\times \displaystyle {\frac{\delta \left( e^{-2d} L_{\mathrm{matter}}\right) }{\delta d}.} \end{aligned}$$(5.3)The general covariance of the action (5.1) under doubled-yet-gauged diffeomorphisms implies the on-shell conservation law,
$$\begin{aligned} \mathcal{D}_{A}T^{AB}\equiv 0, \end{aligned}$$(5.4)which holds up to the equations of motion of the matter fields and consists of \({D+D}\) components.
- \(*\) :
-
The Einstein Double Field Equations (2.88) equate the stringy Einstein tensor and the stringy energy–momentum tensor as
$$\begin{aligned} G_{AB}=8\pi GT_{AB}. \end{aligned}$$(5.5)They comprise the full set of equations of motion for the closed string massless sector, i.e. the stringy graviton fields, \(\{V_{Ap},{\bar{V}}_{B{\bar{q}}},d\}\), which may reduce to the conventional fields, \(\{g_{\mu \nu },B_{\mu \nu },\phi \}\), upon reduction to Riemannian backgrounds. They can also be applied readily to non-Riemannian spacetimes (2.20), [15].
- \(*\) :
-
The further-generalized Lie derivative is defined as (3.4)
$$\begin{aligned} {{\widetilde{\mathcal{L}}}}_{\xi }T_{Mp{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}&\,:=\,&\xi ^{N}\mathcal{D}_{N}T_{Mp{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\&+\omega \mathcal{D}_{N}\xi ^{N}T_{Mp{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\&+2\mathcal{D}_{[M}\xi _{N]}T^{N}{}_{p{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\ {}{} & {} +2\mathcal{D}_{[p}\xi _{q]}T_{M}{}^{q}{}_{{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\&+{{\textstyle \frac{1}{2}}}\mathcal{D}_{[r}\xi _{s]}(\gamma ^{rs})^{\alpha }{}_{\delta }T_{Mp{\bar{p}}}{}^{\delta }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\&-{{\textstyle \frac{1}{2}}}\mathcal{D}_{[r}\xi _{s]}(\gamma ^{rs})^{\delta }{}_{\beta }T_{Mp{\bar{p}}}{}^{\alpha }{}_{\delta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\ {}{} & {} +2\mathcal{D}_{[{\bar{p}}}\xi _{{\bar{q}}]}T_{Mp}{}^{{\bar{q}}\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\beta }}\nonumber \\&+{{\textstyle \frac{1}{2}}}\mathcal{D}_{[{\bar{r}}}\xi _{{\bar{s}}]}(\bar{\gamma }^{{\bar{r}}{\bar{s}}})^{\bar{\alpha }}{}_{\bar{\delta }}T_{Mp{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\delta }}{}_{\bar{\beta }}\nonumber \\&-{{\textstyle \frac{1}{2}}}\mathcal{D}_{[{\bar{r}}}\xi _{{\bar{s}}]}(\bar{\gamma }^{{\bar{r}}{\bar{s}}})^{\bar{\delta }}{}_{\bar{\beta }}T_{Mp{\bar{p}}}{}^{\alpha }{}_{\beta }{}^{\bar{\alpha }}{}_{\bar{\delta }}, \end{aligned}$$(5.6)which is completely covariant for doubled-yet-gauged diffeomorphisms, twofold local Lorentz symmetries, and \(\mathbf {O}(D,D)\) rotations. It is closed by the C-bracket plus twofold local Lorentz transformations, (3.11). Specifically, acting on DFT vielbeins, they read (3.8)
$$\begin{aligned}&{{\widetilde{\mathcal{L}}}}_{\xi }V_{Ap}={\bar{P}}_{A}{}^{B}\left( {\hat{\mathcal{L}}}_{\xi }P_{BC}\right) V^{C}{}_{p} ,\nonumber \\&{{\widetilde{\mathcal{L}}}}_{\xi }{\bar{V}}_{A{\bar{p}}}=P_{A}{}^{B}\left( {\hat{\mathcal{L}}}_{\xi }{\bar{P}}_{BC}\right) {\bar{V}}^{C}{}_{{\bar{p}}}. \end{aligned}$$(5.7)Thus, by setting these further-generalized Lie derivatives to vanish, it becomes possible to characterize the isometry of the doubled-yet-gauged spacetime within the DFT-vielbein formalism.
- \(*\) :
-
The most general \({D=4}\) spherically symmetric ansatzes for both the (Riemannian) stringy graviton fields and the stringy energy–momentum tensor are identified, (4.6), (4.14), which enjoy \(\mathbf {so}(3)\) isometries (4.1), (4.2), (4.3). In particular, with \(K_{\mu \nu }\equiv 2 e_{\mu }{}^{p}\bar{e}_{\nu }{}^{{\bar{q}}}K_{p{\bar{q}}}\), the spherically symmetric energy–momentum tensor may possess not only diagonal but also off-diagonal components, such as generic \(K_{tr}=K_{(tr)}+K_{[tr]}\) and skew-symmetric \(K_{[\vartheta \varphi ]}\) components. The skew-symmetry is a genuine feature of fermionic or stringy matter, (2.117), (2.131), which is induced by their coupling to the B-field.
- \(*\) :
-
The \({D=4}\) Einstein Double Field equations were solved for the most general spherically symmetric, asymptotically flat, static ‘regular’ configurations in which the stringy energy–momentum tensor of the ‘matter’ vanishes completely outside a cutoff radius \(r_{\mathrm{c}}\): \(T_{AB}=0\) for \(r\ge r_{\mathrm{c}}\) (4.22).
Outside the matter, we recover the known vacuum geometry [24] with four constant parameters including electric H-flux, \(\{\alpha ,\beta ,a,h\}\) (4.66),
$$\begin{aligned}&\begin{array}{ccc} {\begin{array}{l} e^{2\phi }=\gamma _{+}\left( \frac{r-\alpha }{r+\beta }\right) ^{\frac{b}{\sqrt{a^{2}+b^{2}}}}+\gamma _{-}\left( \frac{r+\beta }{r-\alpha }\right) ^{\frac{b}{\sqrt{a^{2}+b^{2}}}},\quad H_{\scriptscriptstyle {(3)}}=h\sin \vartheta \,\mathrm{d}t\wedge \mathrm{d}\vartheta \wedge \mathrm{d}\varphi ,\\ \mathrm{d}s^{2}=e^{2\phi }\left[ -\left( \frac{r-\alpha }{r+\beta }\right) ^{\frac{a}{\sqrt{a^{2}+b^{2}}}}\mathrm{d}t^{2} +\left( \frac{r+\beta }{r-\alpha }\right) ^{\frac{a}{\sqrt{a^{2}+b^{2}}}}\big \{\mathrm{d}r^{2}+(r-\alpha )(r+\beta ) \mathrm{d}\Omega ^{2}\big \}\right] \end{array}}&\mathbf {for}&r\ge r_{\mathrm{c}}, \end{array} \end{aligned}$$(5.8)where \(b=\sqrt{(\alpha +\beta )^{2}-a^{2}}\ge 0\,\) or \(\,b=-\sqrt{(\alpha +\beta )^{2}-a^{2}}<0\), and \(\gamma _{\pm }={{\textstyle \frac{1}{2}}}(1\pm \sqrt{1-h^{2}/b^{2}})\). Inside the matter, i.e. \(r<r_{\mathrm{c}}\), while the electric H-flux assumes the same form as outside, magnetic H-flux, i.e. \(H_{r\vartheta \varphi }\), may be present, being sourced by the skew-symmetric angular component, \(K_{[\vartheta \varphi ]}\), c.f. (4.35), (4.37). Crucially, we derive integral expressions for all the constants, \(\{\alpha ,\beta ,a,h\}\), with the integrands given by the stringy energy–momentum tensor (4.67), which thus reveal the physical meanings of the “free” constant parameters in the vacuum geometry. In particular, while in General Relativity a diagonal metric implies a diagonal energy–momentum tensor (A.33) through the Einstein Field Equations, in Stringy Gravity we can have a non-zero off-diagonal component \(K_{(tr)}\) which sources nontrivial electric H-flux and thus modifies the Schwarzschild geometry. This reflects the general nature of Stringy Gravity: the richer stringy energy–momentum tensor – \((D^{2}+1)\) degrees of freedom vs. \(D(D+1)/2\) – enhances the geometry beyond General Relativity.
- \(*\) :
-
We spell out the strong energy condition (4.79) and the pressure condition (4.81), which make \(\alpha \), \(\beta \) and a positive semi-definite (4.83). For the solution to be real and non-degenerate, we postulate that \(r_{\mathrm{c}}\) should exceed \(\alpha \) (4.54). If \(b>0\) and \(h \ne 0\), \(\phi \) decreases from \(\infty \) to a single negative minimum value and then starts to increase monotonically converging to zero as \(r\rightarrow \infty \) (4.84). On the other hand, if \(b<0\), \(\phi \) decreases monotonically from \(\infty \) to zero over the whole range of \(\alpha \le r\le \infty \).
- \(*\) :
-
We consider an effective mass, M(r) (4.87), which is responsible for the centripetal acceleration of circular geodesics,
$$\begin{aligned} \displaystyle {\frac{GM(r)}{R^{2}}=R\left( \frac{\mathrm{d}\varphi }{\mathrm{d}t}\right) ^{2}.} \end{aligned}$$(5.9)Taking the large-r limit, we derive an integral expression for the asymptotic mass (4.93),
$$\begin{aligned} M_{\infty }= & {} \lim _{r\rightarrow \infty }M(r)=\frac{a+ b\sqrt{1-h^{2}/b^{2}}}{2G}\nonumber \\= & {} \displaystyle {\int _{0}^{\infty }\mathrm{d}r\int _{0}^{\pi }\mathrm{d}\vartheta \int _{0}^{2\pi }\mathrm{d}\varphi ~e^{-2d}}\nonumber \\&\times \displaystyle {\left( \frac{1}{8\pi G}\left| H_{t\vartheta \varphi }H^{t\vartheta \varphi }\right| - 2 K_{t}{}^{t} \right) }, \end{aligned}$$(5.10)where the integrand comprises the electric H-flux squared and the stringy energy–momentum component, \(K_{t}{}^{t}\). Requiring \(M_{\infty }\) to be positive-definite amounts to the weak energy condition (4.80).
Compared to the mass formula in GR (A.48), (A.50), the above result (5.10) is in a sense more satisfactory, as the integration is equipped with the proper integral measure in Stringy Gravity, \(e^{-2d}\), while from (2.99), \(K_{t}{}^{t}=-2K_{0}{}^{\bar{0}}\) which is a diffeomorphism scalar.
Rather than requiring the integrand of (5.10) to be strictly positive-definite, namely, the weak energy density condition (4.82), by demanding this only of the whole integral, i.e. the weak energy condition, we may allow M(r) to possibly assume negative values, and hence for gravity to become repulsive for some range of the radius.
While we view Stringy Gravity as a unique string-theory-based alternative to General Relativity, from (5.10) one may regard the H-flux, especially the electric component, as dark matter (c.f. [56]) and \(-2K_{t}{}^{t}\) as the baryonic energy (mass) density.
- \(*\) :
-
As long as \(ab\ne 0\) and \(h\ne 0\), M(r) becomes singular at one finite radius greater than \(\alpha \), \({r=r_{{\scriptscriptstyle {\Omega }}}}>\alpha \). If \(M(r_{{\scriptscriptstyle {\Omega }}})=+\infty \), the gravitational “force” remains attractive and diverges. If the opposite is true, \({M(r_{{\scriptscriptstyle {\Omega }}})=-\infty }\), then there exists an infinite repulsive ‘wall’ located at \(r=r_{{\scriptscriptstyle {\Omega }}}\). Furthermore, when \(\left| b\right| >\left| a\right| \), M(r) admits a single real root which is greater than \(\alpha \): \(M(r_{{\scriptscriptstyle {M}}})=0\), \(r_{{\scriptscriptstyle {M}}}>\alpha \). Thus, with \(M_{\infty }>0\), if \(r_{{\scriptscriptstyle {M}}}\) is either complex (non-physical) or less than \(r_{{\scriptscriptstyle {\Omega }}}\), the gravity is attractive in the entire region from \(r=\infty \) to the singular surface of \(r=r_{{\scriptscriptstyle {\Omega }}}\). On the other hand, if \(r_{{\scriptscriptstyle {M}}}>r_{{\scriptscriptstyle {\Omega }}}\), the gravity is attractive for \(r_{{\scriptscriptstyle {M}}}<r\le \infty \), vanishes at \(r=r_{{\scriptscriptstyle {M}}}\), and becomes repulsive for \(r_{{\scriptscriptstyle {\Omega }}}\le r<r_{{\scriptscriptstyle {M}}}\), encountering the infinite wall at \(r=r_{{\scriptscriptstyle {\Omega }}}\).
- \(*\) :
-
Indeed, when \(\left| b\right| \) is sufficiently large, such as \(\left| b\right| \gtrsim \sqrt{3}\left| a\right| \), the zero of M(r) is guaranteed to exceed the singular radius, \(r_{{\scriptscriptstyle {M}}}>r_{{\scriptscriptstyle {\Omega }}}\). In such cases, gravity (i) remains attractive over the semi-infinite range, \(r_{{\scriptscriptstyle {M}}}<r\le \infty \), featuring Keplerian limiting behavior towards infinity, (ii) vanishes at \(r=r_{{\scriptscriptstyle {M}}}\), and (iii) becomes repulsive in the finite interval \(r_{{\scriptscriptstyle {M}}}<r\le r_{{\scriptscriptstyle {\Omega }}}\), with the infinite wall at \(r=r_{{\scriptscriptstyle {\Omega }}}\). It is then physically reasonable to assume that the cutoff radius should be larger than or equal to the singular radius of the infinite wall, \(r_{\mathrm{c}}\ge r_{{\scriptscriptstyle {\Omega }}}\). Specifically, for non-interacting dust, \(r=r_{\mathrm{c}}\) may well coincide with the surface of zero gravity: \(r_{\mathrm{c}}=r_{{\scriptscriptstyle {M}}}\). This seems to provide a dynamical mechanism to avoid the singularity.
Possible future work includes exhaustive exploration of the parameter space, exploring the causal structure, direct verification of the energy and pressure conditions including the large-\(\left| b\right| \) condition, c.f. (4.72), extensions to non-Riemannian spacetimes, stringy thermodynamics, applications to cosmology, and last but not least, tests against observations.
Notes
In the most general case, the two spin groups can have different dimensions [15].
Consider the power series expansion of \(\Phi _{i}(x+s\Delta )\) around \(s=0\), where we have introduced a real parameter, \(s\in \mathbb {R}\). The linear-order term gives \(\partial _{M}\Phi _{i}\partial ^{M}\Phi _{j}=0\), which in turn, after replacing \(\Phi _{i}\) and \(\Phi _{j}\) by \(\partial _{L}\Phi \) and \(\partial _{N}\Phi \), implies that \(\partial _{L}\partial ^{M}\Phi \partial _{M}\partial ^{N}\Phi =0\). Consequently, \(\partial _{M}\partial ^{N}\Phi \) is a nilpotent matrix and thus must be traceless, \(\partial _{M}\partial ^{M}\Phi =0\) [40].
As an alternative to direct verification, the Bianchi identity can also be shown using (2.7), (2.37) and the relation [49]
$$\begin{aligned} 0= & {} \left. ([{\hat{\mathcal{L}}}_{\zeta },{\hat{\mathcal{L}}}_{\xi }]-{\hat{\mathcal{L}}}_{[\zeta ,\xi ]_{\mathrm{C}}})\right| _{\partial \rightarrow {\nabla }}T_{A_{1}A_{2}\cdots A_{n}}\\= & {} \sum \nolimits _{i=1}^{n}\,6S_{A_{i}[BCD]}\zeta ^{B}\xi ^{C}T_{A_{1}\cdots A_{i-1}}{}^{D}{}_{A_{i+1}\cdots A_{n}}. \end{aligned}$$In the specific case of four-dimensional spacetime with Minkowskian signature \([-+++]\), we may set
$$\begin{aligned} \begin{array}{llll} \left( \gamma ^{p}\right) ^{\dagger }=-A\gamma ^{p}A^{-1},\\ \quad A^{\dagger }=A\quad \Longrightarrow \quad \left( A\gamma ^{p_{1}p_{2}\cdots p_{n}}\right) ^{\dagger }=(-1)^{\frac{1}{2}n(n+1)}A\gamma ^{p_{1}p_{2}\cdots p_{n}},\\ \left( \gamma ^{p}\right) ^{T}=-C\gamma ^{p}C^{-1},\\ \quad C^{T}=-C\quad \Longrightarrow \quad \left( C\gamma ^{p_{1}p_{2}\cdots p_{n}}\right) ^{T}=-(-1)^{\frac{1}{2}n(n+1)}C\gamma ^{p_{1}p_{2}\cdots p_{n}}. \end{array} \end{aligned}$$We may also, if desired, identify A with C and use the Majorana, ti.e. real representation of the gamma matrices. Our analysis also holds for Majorana spinors satisfying \(\psi ^{\dagger }A=\psi ^{T}C\).
Note, e.g. with \(T_{p}=T^{A}V_{Ap}\),
$$\begin{aligned} \left[ {{\widetilde{\mathcal{L}}}}_{\zeta },{{\widetilde{\mathcal{L}}}}_{\xi }\right] T_{p}= & {} \left[ {{\widetilde{\mathcal{L}}}}_{\zeta },{{\widetilde{\mathcal{L}}}}_{\xi }\right] \left( T^{A}V_{Ap}\right) \\= & {} \left( \left[ {{\widetilde{\mathcal{L}}}}_{\zeta },{{\widetilde{\mathcal{L}}}}_{\xi }\right] T^{A}\right) V_{Ap}+ T^{A}\left[ {{\widetilde{\mathcal{L}}}}_{\zeta },{{\widetilde{\mathcal{L}}}}_{\xi }\right] V_{Ap}\\= & {} \left( {{\widetilde{\mathcal{L}}}}_{\left[ \zeta ,\xi \right] _{\mathrm{C}}}T^{A}\right) V_{Ap}+ T^{A}\left( {{\widetilde{\mathcal{L}}}}_{\left[ \zeta ,\xi \right] _{\mathrm{C}}}V_{Ap}+\omega _{pq}(\zeta ,\xi )V_{A}{}^{q}\right) \\= & {} {{\widetilde{\mathcal{L}}}}_{\left[ \zeta ,\xi \right] _{\mathrm{C}}}\left( T^{A}V_{Ap}\right) +\omega _{pq}(\zeta ,\xi )T^{q}\\= & {} {{\widetilde{\mathcal{L}}}}_{\left[ \zeta ,\xi \right] _{\mathrm{C}}}T_{p}+\omega _{pq}(\zeta ,\xi )T^{q}. \end{aligned}$$In terms of Cartesian coordinates, \(x^{1}=r\sin \vartheta \cos \varphi , \,x^{2}=r\sin \vartheta \sin \varphi , \,x^{3}=r\cos \vartheta \), we have
$$\begin{aligned} \sin \vartheta \,\mathrm{d}\vartheta \wedge \mathrm{d}\varphi ={{\textstyle \frac{1}{2}}}\epsilon _{ijk}(x^{i}/r^{3})\,\mathrm{d}x^{j}\wedge \mathrm{d}x^{k}. \end{aligned}$$Strictly speaking, we might relax the pressure condition (4.81) and require \(\widetilde{\mathcal{Z}}_{\mathrm{c}}\ge 0\) only. However we do not pursue this here.
For the case of \(h=0\), see (4.97).
However, the mass, \(M_{\infty }\), does not coincide with the time-translational Noether charge (4.78) for the Killing vector \(\xi ^{\mu }\partial _{\mu }=\partial _{t}\), nor the ADM mass a la Wald, \(GM_{{\mathrm{ADM}}}={{\textstyle \frac{1}{4}}}\left[ \textstyle {a+\left( \frac{a-b}{a+b}\right) \sqrt{a^{2}+b^{2}}}\right] \) [24] (c.f. [23, 55]).
References
T.H. Buscher, A symmetry of the string background field equations. Phys. Lett. B 194, 59 (1987)
T.H. Buscher, Path integral derivation of quantum duality in nonlinear sigma models. Phys. Lett. B 201, 466 (1988)
W. Siegel, Two Vierbein formalism for string inspired axionic gravity. Phys. Rev. D 47, 5453 (1993)
W. Siegel, Superspace duality in low-energy superstrings. Phys. Rev. D 48, 2826 (1993)
C. Hull, B. Zwiebach, Double field theory. JHEP 0909, 099 (2009)
C. Hull, B. Zwiebach, The Gauge algebra of double field theory and Courant brackets. JHEP 0909, 090 (2009)
O. Hohm, C. Hull, B. Zwiebach, Background independent action for double field theory. JHEP 1007, 016 (2010)
O. Hohm, C. Hull, B. Zwiebach, Generalized metric formulation of double field theory. JHEP 1008, 008 (2010)
I. Jeon, K. Lee, J.H. Park, Stringy differential geometry, beyond Riemann. Phys. Rev. D 84, 044022 (2011). arXiv:1105.6294 [hep-th]
I. Jeon, K. Lee, J.H. Park, Incorporation of fermions into double field theory. JHEP 1111, 025 (2011). https://doi.org/10.1007/JHEP11(2011)025. arXiv:1109.2035 [hep-th]
M.J. Duff, Hidden string symmetries? Phys. Lett. B 173, 289 (1986)
A. Coimbra, C. Strickland-Constable, D. Waldram, Supergravity as generalised geometry I: type II theories. JHEP 1111, 091 (2011)
K.S. Choi, J.H. Park, Standard model as a double field theory. Phys. Rev. Lett. 115(17), 171603 (2015)
J.H. Park, Stringy gravity: solving the dark problems at short distance. EPJ Web Conf. 168, 01010 (2018). https://doi.org/10.1051/epjconf/201816801010. arXiv:1707.08961 [hep-th]
K. Morand, J.H. Park, Classification of non-Riemannian doubled-yet-gauged spacetime. Eur. Phys. J. C 77(10), 685 (2017). https://doi.org/10.1140/epjc/s10052-017-5257-z. arXiv:1707.03713 [hep-th]
E. Bergshoeff, Applied Newton–Cartan Geometry, review talk at Simons Center. http://scgp.stonybrook.edu/video_portal/video.php?id=3051. Accessed 7 Mar 2017
J. Gomis, H. Ooguri, Nonrelativistic closed string theory. J. Math. Phys. 42, 3127 (2001)
S.M. Ko, C. Melby-Thompson, R. Meyer, J.H. Park, Dynamics of perturbations in double field theory & non-relativistic string theory. JHEP 1512, 144 (2015). arXiv:1508.01121 [hep-th]
W. Siegel, Amplitudes for left-handed strings. arXiv:1512.02569 [hep-th]
I. Jeon, K. Lee, J.H. Park, Supersymmetric double field theory: stringy reformulation of supergravity. Phys. Rev. D 85 081501 (2012) (erratum: Phys. Rev. D 86, 089903(E), 2012)
I. Jeon, K. Lee, J.H. Park, Y. Suh, Stringy unification of type IIA and IIB supergravities under N = 2 D = 10 supersymmetric double field theory. Phys. Lett. B 723, 245 (2013)
J.H. Park, Green–Schwarz superstring on doubled-yet-gauged spacetime. JHEP 1611, 005 (2016). arXiv:1609.04265 [hep-th]
J.H. Park, S.J. Rey, W. Rim, Y. Sakatani, \(\mathbf{o}(D, D)\) covariant Noether currents and global charges in double field theory. JHEP 1511, 131 (2015). arXiv:1507.07545 [hep-th]
S.M. Ko, J.H. Park, M. Suh, The rotation curve of a point particle in stringy gravity. JCAP 1706(06), 002 (2017). https://doi.org/10.1088/1475-7516/2017/06/002. arXiv:1606.09307 [hep-th]
C.P. Burgess, R.C. Myers, F. Quevedo, On spherically symmetric string solutions in four-dimensions. Nucl. Phys. B 442, 75 (1995). https://doi.org/10.1016/S0550-3213(95)00090-9. arXiv:hep-th/9410142
S. Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley, New York, 1972). ISBN-10: 0471925675
R.L. Arnowitt, S. Deser, C.W. Misner, Gen. Relat. Grav. 40, 1997 (2008)
R.M. Wald, Black hole entropy is the Noether charge. Phys. Rev. D 48, 3427 (1993). arXiv:gr-qc/9307038
V. Iyer, R.M. Wald, Some properties of Noether charge and a proposal for dynamical black hole entropy. Phys. Rev. D 50, 846 (1994). arXiv:gr-qc/9403028
V. Iyer, R.M. Wald, A Comparison of Noether charge and Euclidean methods for computing the entropy of stationary black holes. Phys. Rev. D 52, 4430 (1995). arXiv:gr-qc/9503052
W. Kim, S. Kulkarni, S.H. Yi, Quasilocal conserved charges in a covariant theory of gravity. Phys. Rev. Lett. 111(8), 081101 (2013)
W. Kim, S. Kulkarni, S.H. Yi, Quasilocal conserved charges in a covariant theory of gravity. Phys. Rev. Lett. 112(7), 079902 (2014)
S. Hyun, S.A. Park, S.H. Yi, Quasi-local charges and asymptotic symmetry generators. JHEP 1406, 151 (2014). arXiv:1403.2196 [hep-th]
G. Aldazabal, D. Marques, C. Nunez, Double field theory: a pedagogical review. Class. Quantum Grav. 30, 163001 (2013). arXiv:1305.1907 [hep-th]
D.S. Berman, D.C. Thompson, Duality symmetric string and m-theory. Phys. Rep. 566, 1 (2014). arXiv:1306.2643 [hep-th]
O. Hohm, D. Lust, B. Zwiebach, The spacetime of double field theory: review, remarks, and outlook. Fortsch. Phys. 61, 926 (2013). arXiv:1309.2977 [hep-th]
D.S. Berman, C.D.A. Blair, E. Malek, M.J. Perry, The \(O_{D, D}\) geometry of string theory. Int. J. Mod. Phys. A 29, 1450080 (2014)
M. Cederwall, The geometry behind double geometry. JHEP 1409, 070 (2014)
J.H. Park, Comments on double field theory and diffeomorphisms. JHEP 1306, 098 (2013). arXiv:1304.5946 [hep-th]
K. Lee, J.H. Park, Covariant action for a string in doubled yet gauged spacetime. Nucl. Phys. B 880, 134 (2014)
C.M. Hull, Doubled geometry and T-folds. JHEP 0707, 080 (2007). arXiv:hep-th/0605149
C.D.A. Blair, Particle actions and brane tensions from double and exceptional geometry. JHEP 1710, 004 (2017). https://doi.org/10.1007/JHEP10(2017)004. arXiv:1707.07572 [hep-th]
J.I. Sakamoto, Y. Sakatani, Local \(\beta \)-deformations and Yang–Baxter sigma model. arXiv:1803.05903 [hep-th]
A.S. Arvanitakis, C.D.A. Blair, Type II Strings are Exceptional. arXiv:1712.07115 [hep-th]
A.S. Arvanitakis, C.D.A. Blair, The Exceptional Sigma Model. arXiv:1802.00442 [hep-th]
I. Jeon, K. Lee, J.H. Park, Ramond–Ramond cohomology and \(O(D, D)\) T-duality. JHEP 1209, 079 (2012)
A. Rocen, P. West, E11, generalised space-time and IIA string theory: the R–R sector. https://doi.org/10.1142/9789814412551-0020. arXiv:1012.2744 [hep-th]
I. Jeon, K. Lee, J.H. Park, Double field formulation of Yang–Mills theory. Phys. Lett. B 701, 260 (2011). arXiv:1102.0419 [hep-th]
I. Jeon, K. Lee, J.H. Park, Differential geometry with a projection: application to double field theory. JHEP 1104, 014 (2011)
W. Cho, J.J. Fernndez-Melgarejo, I. Jeon, J.H. Park, Supersymmetric gauged double field theory: systematic derivation by virtue of twist. JHEP 1508, 084 (2015)
O. Hohm, B. Zwiebach, On the Riemann tensor in double field theory. JHEP 1205, 126 (2012)
O. Hohm, S.K. Kwak, B. Zwiebach, Unification of type II strings and T-duality. Phys. Rev. Lett. 107, 171603 (2011). https://doi.org/10.1103/PhysRevLett.107.171603. arXiv:1106.5452 [hep-th]
O. Hohm, S.K. Kwak, B. Zwiebach, Double field theory of type II strings. JHEP 1109, 013 (2011). https://doi.org/10.1007/JHEP09(2011)013. arXiv:1107.0008 [hep-th]
E. Bergshoeff, R. Kallosh, T. Ortin, D. Roest, A. Van Proeyen, New formulations of \(\text{ D } = 10\) supersymmetry and D8–O8 domain walls. Class. Quantum Grav. 18, 3359 (2001)
C.D.A. Blair, Conserved currents of double field theory. JHEP 1604, 180 (2016)
Y.K.E. Cheung, F. Xu, Fitting the Galaxy Rotation Curves: Strings Versus NFW Profile. arXiv:0810.2382 [hep-th]
Acknowledgements
We wish to thank Chris Hull, Hyun Gyu Kang, Kevin Morand for helpful discussions, and Chaiho Rim for generous support. This work was supported by the National Research Foundation of Korea through the Grant 2016R1D1A1B01015196.
Author information
Authors and Affiliations
Corresponding author
A C20 GR prior to C21 DFT
A C20 GR prior to C21 DFT
In this Appendix, after reviewing the energy–momentum tensor and Einstein Field Equations in GR, we discuss the most general static spherically symmetric regular solution in four-dimensional spacetime.
1.1 A.1 Energy–momentum tensor and Einstein field equations in GR
Let us consider the Einstein–Hilbert action coupled to generic matter,
where \(L_{\mathrm{matter}}\) is the Lagrangian for various matter fields, which we denote by \(\Upsilon _{a}\). The energy–momentum tensor is conventionally defined by
where \(\frac{\delta \quad }{\delta g^{\mu \nu }}\) is the standard functional derivative which is best computed from the infinitesimal variation of the Lagrangian density induced by \(\delta g^{\mu \nu }\), as
where the disregarded total derivatives appear generically, since \(L_{\mathrm{matter}}\) includes covariant derivatives of the form \({\bigtriangledown }_{\mu }\Upsilon _{a}\), and the connections contain the derivatives of the metric. The right-hand side of (A.3) then gives, or operationally defines, the functional derivative, \(\frac{\,\delta L_{\mathrm{matter}}\,}{\delta g^{\mu \nu }}\), as the functional ‘coefficient’ of \(\sqrt{-g}\,\delta g^{\mu \nu }\). It is also useful to note that if we vary not the Lagrangian density but the weightless scalar, \(L_{\mathrm{matter}}\), covariant total derivatives of the form ‘\({\bigtriangledown }_{\mu }J^{\mu }\)’ will appear and should be neglected,
Of course, when \( L_{\mathrm{matter}}\) involves fermions,
one should consider a priori the variation of the vielbein rather than the metric,

Up to the fermionic equations of motion,
we note that
Here the equivalence symbol, ‘\(\equiv \)’, denotes on-shell equality which holds up to the equations of motion of the matter fields. Using this relation and disregarding any total derivatives (\(\simeq \)), we derive the variation of the fermionic Lagrangian, \(\sqrt{-g}L_{\mathrm{fermion}}\) (A.5), given by
This result shows that even for fermions, the definition of the energy–momentum tensor through the ‘metric’ variation (A.2) is in a sense still valid, leading to the following ‘symmetric’ contribution,
That is to say, the energy–momentum tensor is always symmetric in GR.Footnote 14 In fact, this can be shown in a more general setup. The arbitrary variation of the vielbein decomposes into two parts,
of which the last term can be viewed as the infinitesimal local Lorentz transformation of the vielbein. Since \(L_{\mathrm{matter}}\) is supposed to be a singlet of local Lorentz symmetry, using (A.11) the generic variation of \(L_{\mathrm{matter}}\) can be written as
Here the dots, ‘\(\cdots \)’, denote any disregarded covariant total derivatives; \(\delta ^{\prime }\Upsilon _{a}\) is the arbitrary variation of the matter field supplemented by the infinitesimal local Lorentz rotation, \(\delta e_{\nu }{}^{[a}e^{b]\nu }\). Further, \(\frac{\delta L_{\mathrm{matter}}}{\delta \Upsilon _{a}}\) corresponds to the Euler–Lagrange equation for each matter field, \(\Upsilon _{a}\). Thus, the energy–momentum tensor (A.2) is ‘on-shell’ equivalent to
Now for the Einstein–Hilbert term, it is useful to remember that the variation of the Riemann curvature is given by covariant total derivatives,
such that
and
Bringing this all together, while disregarding any surface integral, the arbitrary variation of the action reads
Clearly the equation of motion of the metric leads to the (undoubled) Einstein Field Equations,
which are equivalent to
In particular, when the variation is caused by diffeomorphisms, i.e. \(\delta g^{\mu \nu }=\mathcal{L}_{\xi }g^{\mu \nu }=-2{\bigtriangledown }^{(\mu }\xi ^{\nu )}\), the action should be invariant. From (A.17), we get, up to the equations of motion, \(\frac{\delta L_{\mathrm{matter}}}{\delta \Upsilon _{a}}\equiv 0\), and up to surface integrals,
This should hold for arbitrary \(\xi ^{\mu }\), e.g. highly localized delta-function-type vector fields. Therefore the Einstein curvature and the energy–momentum tensor should be conserved off-shell and on-shell, respectively,
As is well known, the former can also be obtained directly from the Bianchi identity, \({\bigtriangledown }_{[\lambda }R_{\mu \nu ]\rho \sigma }=0\).
For any Killing vector satisfying the isometric condition,
the conservation of the energy–momentum tensor (A.21) implies the existence of a conserved Noether current,
which in turn defines a Noether charge,
1.2 A.2 Regular spherically symmetric solution in \({D=4}\) GR
Here we derive the most general, asymptotically flat, spherically symmetric, static, regular solution to the \(D=4\) Einstein Field Equations. We require the metric and energy–momentum tensor to be spherically symmetric,
with three Killing vectors, \(\xi ^{\mu }_{a}\), \(a=1,2,3\), corresponding to the usual angular momentum differential operators,
They satisfy the \(\mathbf {so}(3)\) commutation relation,
It follows from (A.25) that
Furthermore, without loss of generality, we can put \({g_{tr}=0}\), \(\,{g_{\vartheta \vartheta }=r^{2}}\), and set the metric to be diagonal, utilizing diffeomorphisms (see e.g. [26]),
where we put as shorthand notation,
The nonvanishing Christoffel symbols are then exhaustively,
and subsequently the Ricci curvature, \(R_{\mu \nu }\), becomes diagonal, with components
Since both the Ricci curvature and the metric are diagonal, the Einstein Field Equations imply that the energy–momentum tensor must also be diagonal, thus fixing \(T_{tr}=0\),
Now the conservation of the energy–momentum tensor, \({\bigtriangledown }_{\mu }T^{\mu }{}_{\nu }\), boils down to a single equation:
The Einstein Field Equations, or (A.19), reduce to
which are linearly equivalent to
The first equation can be integrated to give
where we have assumed ‘regularity’ at the origin,
This fixes the function A(r),
for which we have defined
The regularity condition (A.38) is then equivalent to
Furthermore, the positive energy (density) condition implies \(T^{tt}\ge 0\), such that, owing to the convention of the mostly plus signature of the metric (A.29), M(r) is generically positive. Similarly, assuming the ‘flat’ boundary condition at infinity,
the second equation in (A.36) can be integrated to fix B(r),
such that the metric takes the final form:
Here M(r) is given by (A.40) and \(\Delta (r)\) is defined by
Finally, we show that, up to the first and the second relations in (A.36) and their solutions, (A.39), (A.43), the third relation is equivalent to the conservation of the energy–momentum tensor (A.34). For this, we solve for \(T^{r}{}_{r}\) and \(T^{r}{}_{r}-T^{t}{}_{t}\) from the first and the second relations in (A.36),
and substitute these two expressions into the left-hand side of the conservation relation (A.34), to obtain
This result clearly establishes the equivalence between the energy–momentum conservation equation (A.34) and the third relation in (A.36).
Some comments are in order.
-
When the matter is localized up to a finite radius \(r_{c}\), such that outside this radius, \({r>r_{c}}\), we have \(T_{\mu \nu }(r)=0\) and \(\Delta (r)=0\), we recover the Schwarzschild solution, in which the mass agrees with the ADM mass [27] and from (A.40) is further given by the volume integral,
$$\begin{aligned} M=-\int _{0}^{r_{c}}\mathrm{d}r\, 4\pi r^{2\,} T^{t}{}_{t}(r)=-\int _{0}^{\infty }\mathrm{d}r\, 4\pi r^{2\,} T^{t}{}_{t}(r). \end{aligned}$$(A.48)However, this differs from the Noether charge (A.24) of the time translational Killing vector,
$$\begin{aligned} M\ne -Q[\partial _{t}]=-\int _{0}^{\infty }\mathrm{d}r\, 4\pi r^{2\,}e^{-\Delta (r)\,} T^{t}{}_{t}(r), \end{aligned}$$(A.49)since from (A.38) the integral measure is nontrivial,
$$\begin{aligned} \sqrt{-g}=e^{-\Delta (r)\,}r^{2}\sin \vartheta \ne r^{2}\sin \vartheta . \end{aligned}$$(A.50)This discrepancy and its remedy by an extra surface integral are rather well known, see [28,29,30,31,32,33].
-
If there is a spherical void in which \(T_{\mu \nu }=0\) for \(r_{1}<r<r_{2}\), both M(r) and \(\Delta (r)\) become constant inside the void as \(M(r)=M(r_{1})\) and \(\Delta (r)=\Delta (r_{2})\). After a constant rescaling of the time, \(t_{\mathrm{new}}=e^{-\Delta (r_{2})}t\), the local geometry inside the void coincides precisely with the Schwarzschild solution. We note that the mass is determined through the integral over \(0<r<r_{1}\) only and is independent of the matter distribution outside, \(r>r_{2}\). While this is certainly true in Newtonian gravity (namely the iron sphere theorem), if we solved the vacuum Einstein Field Equations with vanishing energy–momentum tensor inside the void, we would merely recover the Schwarzschild geometry in accordance with Birkhoff’s theorem. Nevertheless it would be hard to conclude that the constant mass parameter is unaffected by the outer region.
-
The radial derivative of B(r) amounts to the gravitational acceleration for a circular geodesic [24],
$$\begin{aligned} r\left( \frac{\mathrm{d}\vartheta }{\mathrm{d}t}\right) ^{2}= & {} -\frac{1}{2}\frac{\mathrm{d}g_{tt}(r)}{\mathrm{d}r}={{\textstyle \frac{1}{2}}}B^{\prime }\nonumber \\= & {} \left[ \frac{GM(r)}{r^{2}}+4\pi Gr T^{r}{}_{r}(r)\right] e^{-2\Delta (r)}. \nonumber \\ \end{aligned}$$(A.51)Again, inside a void or the outer vacuum region, we may absorb the constant factor of \(e^{-2\Delta (r)}\) into the rescaled time, and thus recover the Keplerian acceleration,
$$\begin{aligned} r\left( \frac{\mathrm{d}\vartheta }{\mathrm{d}t}\right) ^{2}=\frac{GM}{r^{2}}. \end{aligned}$$(A.52)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Angus, S., Cho, K. & Park, JH. Einstein double field equations. Eur. Phys. J. C 78, 500 (2018). https://doi.org/10.1140/epjc/s10052-018-5982-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5982-y