Elastic amplitudes studied with the LHC measurements at 7 and 8 TeV

Abstract

Recent measurements of the differential cross sections in the forward region of pp elastic scattering at 7 and 8 TeV show the precise form of the t dependence. We present a detailed analysis of these measurements including the structures of the real and imaginary parts of the scattering amplitude. A good description is achieved, confirming in all experiments the existence of a zero in the real part in the forward region close to the origin, in agreement with the prediction of a theorem by Martin, with an important role in the observed form of $\mathrm{d}\sigma /\mathrm{d}t$. A universal value for the position of this zero and regularity in other features of the amplitudes are found, leading to quantitative predictions for the forward elastic scattering at 13 TeV.

1 LHC experiments in elastic $\mathrm{pp}$ scattering

With an enormous gap in the center-of-mass energy with respect to previous data in pp and p${\bar{\mathrm{p}}}$ scattering, the Totem and Atlas experimental groups at LHC have recently measured $\mathrm{d}\sigma /\mathrm{d}t$ in the forward t ranges at $\sqrt{s}$ = 7 and 8 TeV [1,2,3,4,5]. These measurements offer a unique opportunity to investigate the behavior of p-p collisions at the highest energies reached in laboratory. A detailed and precise analysis of these data can establish a precious milestone for the understanding of the high energy behavior of p-p interactions. The datasets and their t ranges are listed in Table 1, where we use the obvious notation T7, T8, A7, A8 to specify Totem (T) and Atlas (A) Collaborations and center-of-mass energies 7 and 8 TeV.

Table 1 Measurements at $\sqrt{s}=$7 and 8 TeV from Totem and Atlas Collaborations at LHC [1,2,3,4,5]. The $\rho$ values for $^\mathrm{a}$ $^\mathrm{b}$ are taken from COMPETE Collaboration [19]. For $^\mathrm{c}$ the $\rho$ value was obtained by the authors with a forward SET-I and kept fixed in a complete SET-II as explained in the section with the analysis of T8. For $^\mathrm{d}$ the $\rho$ value is taken from [18]

In order to build a bridge towards theoretical models aiming at the understanding of the dynamics, it is important that the analysis of these LHC data be made with identification of the structures of the individual parts of the complex scattering amplitude. The disentanglement of the two terms in the observed modulus $\mathrm{d}\sigma /\mathrm{d}t$ is the crucial task. At each energy, parameterizations must search to exhibit clearly the properties of magnitudes, signs, slopes and zeros of the real and imaginary parts. External support, as dispersion relations and connections with analyses at other energies, gives important clues. The intervention of the electromagnetic interactions must be treated coherently with a proposed analytical form for the nuclear part, and account must be taken of phase of the Coulomb–Nuclear Interference (CNI), which is calculated in Appendix A.

In the present work we perform a detailed examination of the data trying to satisfy these requirements. Each part of the amplitude is written with an exponential factor with a slope, multiplying a linear term in t, thus with three parameters. These analytical forms are sufficient to describe the properties of the nuclear parts. The six parameters for each dataset are studied using fits to data with appropriate statistical control. Correlations are studied, and resulting values are proposed for each dataset. Good description of the measurements is obtained, with details in the shape of the forward diffractive peak, exhibiting the zero of the real part predicted in the theorem by Martin [6], and with observation in the forward range of the ingredients that construct the imaginary zero responsible for the dip in $\mathrm{d}\sigma /\mathrm{d}t$ observed when data exist at higher |t|.

According to analyses and models of pp and p${\bar{\mathrm{p}}}$ scattering at high energies [7,8,9,10,11,12,13,14,15,16], including full-t ranges, the imaginary part has a zero near the marked dip observed in $\mathrm{d}\sigma /\mathrm{d}t$ at about 0.4–0.6 $\text{ GeV }^2$, while the real part starts positive at $t=0$, has a zero for small |t| (Martin’s theorem), and a second zero after the dip. The descriptions of the models differ for higher |t| about the position of this second real zero and about the existence of further imaginary or real zeros. Models describing large |t| ranges have different motivations and dynamical structures, and may be analytically very sophisticated, trying to represent the observed shapes of dip, bump, tail, in the angular dependence. However, in the forward range the analytical structure required to describe the data may be very simple. In the present work we show that real and imaginary parts including exponential slopes and linear factors, combined with the electromagnetic interference, contain the essential ingredients for a precise representation. The second real zero occurs outside the studied range and does not influence the analysis. Particularly due to the small magnitude of the $\rho$ parameter, the disentanglement of the two parts is not trivial, requiring careful analysis, and still leaving room for some subjective but physically reasonable choice. Once the amplitudes are identified, the results provide a necessary connection between data and theoretical models of microscopic nature for the strong interaction dynamics.

The deviation from the pure exponential form in $\mathrm{d}\sigma /\mathrm{d}t$ is obvious beforehand, since $\mathrm{d}\sigma /\mathrm{d}t$ is a sum of two independent squares. More clarity can be obtained in the analysis with the identification of the two parts of the complex amplitude and their control by fundamental constraints (dispersion relations, Martin’s theorem for the real part, zero of the imaginary part anticipating the dip).

Of the four datasets, T8 is the only one reaching very small |t|, allowing for a more complete investigation of some details, such as the influence of the Coulomb phase. However, a comparative analysis of the four cases is extremely important, since on observing coherence in some characteristics we may believe that there is reliability in the descriptions. The energy dependence of pp elastic scattering is very smooth, and features of 7 and 8 TeV data must support each other in a unified treatment.

A theorem by Martin proves that the real part has a zero close to the origin [6]. The abstract of the paper says, literally

We show that if for fixed negative (physical) square of the momentum transfer t, the differential cross section ${d}\sigma /{d}t$ tends to zero and if the total cross section tends to infinity, when the energy goes to infinity, the real part of the even signature amplitude cannot have a constant sign near $t=0$. @ 1997 Elsevier Science B.V.

Thus the real part in pp and p${\bar{\mathrm{p}}}$ scattering has a zero close to the origin, with location approaching $t=0$ as the energy increases. This constraint has been confirmed in previous analyses at LHC and lower energies [7, 8], with the conclusion that the position of the first zero of the real part behaves like $|t_R| ~= A+ 1/(c_0 +c_1 ~\log {s}+ c_2 ~\log ^2{s}).$

Although the analytical properties of the amplitude are defined in t-space, the insights for the construction of theoretical models are natural in the geometrical space, where the physical intuition to build amplitudes may be represented. The Fourier transformed space is appropriate to study asymptotic properties of the cross sections such as questioning whether the proton behaves as a black or a gray disk. The profile functions are also convenient tools to study the unitarity constraint. Of course, we recognize that the amplitudes written for the short forward t-range cannot lead to a sufficient understanding of b-space properties. Even so, we believe that the relationship is important, and the Fourier transformation of our amplitudes to b-space is analytically performed and its properties are discussed in Appendix B.

This paper is organized as follows. Section 2 describes the formalism of the proposed model; Sect. 3 presents the results of the model fits to the four LHC measurements; Sect. 4 summarizes the numerical analysis; Sect. 5 concludes the paper.

2 Amplitudes and observables in forward scattering

In the analysis limited to the forward ranges shown in Table 1, the expectations are satisfied writing the differential cross section in the form

$$\begin{aligned}&\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\pi \left( \hbar c\right) ^{2} \nonumber \\&\quad \times \bigg \{\bigg [\frac{\sigma (\rho -\mu _R t) }{4\pi \left( \hbar c\right) ^{2}}~{{e}^{B_{R}t/2} +F^{C}(t)\cos {(\alpha \phi )}\bigg ]^{2}}\nonumber \\&\quad +\bigg [\frac{\sigma (1-\mu _I t)}{4\pi \left( \hbar c\right) ^{2}}~{{e}^{B_{I}t/2} +F^{C}(t)\sin {(\alpha \phi )}\bigg ]^{2}\bigg \}} \end{aligned}$$

(1)

where $t\equiv -|t|$, $\alpha$ is the fine structure constant and $(\hbar c)^2=0.3894$ mb $\text{ GeV }^2$. This expression is applied for pp an p${\bar{\mathrm{p}}}$, and the parameters are specific for each case. $F^C(t)$ and $\alpha \phi (t)$ represent the form factor and phase of the Coulomb interaction. The phase $\alpha \phi$ has opposite signs for pp and p${\bar{\mathrm{p}}}$ scattering.

The real electromagnetic amplitude is given in terms of the proton form factor

$$\begin{aligned} F^{C}(t)~=(-/+)~\frac{2\alpha }{|t|}~F_{\mathrm {proton}}^{2}(t)~, \end{aligned}$$

(2)

for the pp / p${\bar{\mathrm{p}}}$ collisions. The proton form factor is taken as

$$\begin{aligned} F_{\mathrm {proton}}(t)=[\Lambda ^2/(\Lambda ^2+|t|)]^{2}~, \end{aligned}$$

(3)

where $\Lambda ^2=0.71 \text{ GeV }^{2}$. The phase of the Coulomb–Nuclear interference is discussed in Appendix A.

We have thus assumed the imaginary amplitude with an exponential that accounts for the forward diffractive peak and a linear factor that accounts for the zero that occurs near the dip in $\mathrm{d}\sigma /\mathrm{d}t$, writing the simple form

$$\begin{aligned} T_I^N (t)= \frac{1}{4 \sqrt{\pi }\left( \hbar c\right) ^2 } ~ \sigma ( 1 -\mu _I t )~ e^{B_I t/2} ~ \end{aligned}$$

(4)

and

$$\begin{aligned} T_I(t)=T_I^N (t)+\sqrt{\pi } F^C(t) \sin (\alpha \phi ). \end{aligned}$$

(5)

The influence of the parameter $\mu _I$ depends on the range of the data analyzed. To include the influence of the first real zero, we write

$$\begin{aligned} T_R^N(t)= \frac{1}{4 \sqrt{\pi } \left( \hbar c\right) ^2} ~ \sigma (\rho -\mu _R t) ~ e^{B_R t/2} \end{aligned}$$

(6)

and

$$\begin{aligned} T_R(t)=T_R^N(t)+\sqrt{\pi } F^C(t) \cos (\alpha \phi ). \end{aligned}$$

(7)

In order to check the influence of a second zero in the real part, we could add in the amplitude a term $\xi _R~ t^2$, but actually it has no effect in the present analysis.

The normalization is defined by

$$\begin{aligned} \sigma (s)= 4\sqrt{\pi }(\hbar c)^2 ~T_I^N(s,t=0) \end{aligned}$$

(8)

and for the pure nuclear interaction

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}= (\hbar c)^2 [(T_I^N)^2+(T_R^N)^2] ~. \end{aligned}$$

(9)

At $t=0$, we have the usual definition of the $\rho$ parameter

$$\begin{aligned} \rho = \frac{T_R^N(0)}{T_I^N(0)}. \end{aligned}$$

(10)

With positive $\rho$ and negative $\mu _R$ (this is what we have in pp at high energies, as our analysis shows), there is a zero in the real amplitude, namely Martin’s zero, located at

$$\begin{aligned} t_R = \frac{\rho }{\mu _R}~. \end{aligned}$$

(11)

The position of this zero and the magnitudes of the real and imaginary amplitudes in its neighborhood are responsible for details in the deviation of the differential cross section from a pure exponential behavior.

The derivatives of the nuclear amplitudes at $t=0$ are

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\log T_I^N (t)\bigg |_0= \frac{1}{2}[B_I-2 \mu _I]= \frac{1}{2} B_I^\mathrm{eff} \end{aligned}$$

(12)

and

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \log T_R^N (t)\bigg |_0= \frac{1}{2}\left[ B_R-2 \frac{\mu _R}{\rho }\right] = \frac{1}{2} B_R^\mathrm{{eff}}. \end{aligned}$$

(13)

The average slope measured directly in $\mathrm{d}\sigma /\mathrm{d}t$ is the quantity

$$\begin{aligned} B= \frac{2}{(\mathrm{d}\sigma /\mathrm{d}t)\bigg |_0} \left[ \frac{\mathrm{d}}{\mathrm{d}t}(\mathrm{d}\sigma /\mathrm{d}t)\right] \bigg |_0= \frac{1}{1+\rho ^2} \big [B_I^\mathrm{{eff}}+\rho ^2 B_R^\mathrm{{eff}}\big ]. \end{aligned}$$

(14)

We remark that parameters are determined fitting data in limited |t| ranges, at finite distance from the origin, so that the values obtained depend on the analytical forms (4), (5), (6), and (7) of the amplitudes. In particular, the slope parameter usually written in the form $\mathrm{d}\sigma /\mathrm{d}t= \sigma ^2 (\rho ^2+1) \exp (Bt)$ does not agree with the expression for the differential cross section as sum of two independent squared magnitudes, each with its own slope. The assumption that $B_R$ and $B_I$ are equal is not justified. The average quantity B alone gives rough and unsatisfactory information. The importance of the different slopes in the analysis of pp elastic scattering has been investigated in the framework of the so-called dispersion relations for slopes [17]. It is important to note that also the Coulomb–Nuclear phase $\phi (t)$ depends essentially on the form of the nuclear amplitudes [20, 21]. In Appendix A, generalizing previous work [7, 22,23,24], we derive the expression for the phase to be used with the assumed amplitudes written above.

Of course the six parameters are correlated, and in the present work we investigate the bounds of the correlations. We attempt to identify the values of parameters that may be considered as common representatives for different measurements. We show that the differences between the two experimental collaborations may be restricted to quantities characterizing normalization. The question of normalization is essential, and our inputs are the values of $\mathrm{d}\sigma /\mathrm{d}t$ given in the experimental literature [1,2,3,4,5].

The extraction of forward parameters in the pp scattering has difficulties due to the small value of the $\rho$ parameter, and consequently has suffered in many analyses from neglect of the properties of the real part. In our view the values of $\sigma$, $\rho$, B appearing in universal databases [18, 19] as if they were direct experimental measurements should give room for critically controlled phenomenological determinations. A proper consideration for the properties of the complex amplitude is necessary. We observe that the properties that $B_R \ne B_I$ and of the presence of zeros are common to several models [7,8,9,10,11,12,13,14,15,16]. The determination of the amplitudes for all |t| in several models is coherent.

We observe that the polynomial factors written in the exponent in some parameterizations of data [3, 4] correspond to the linear and quadratic factors mentioned above, if the assumption is made that they are much smaller than 1 and can be converted into exponentials. However, this substitution is not convenient, because it does not show explicitly the essential zeros, and it also gives an unsatisfactory parameterization that cannot be extended even to nearby |t| values.

We thus have the framework necessary for the analysis of the data, with clear identification of the role of the free parameters. The quantities to be determined for each dataset are $\sigma$, $\rho$, $B_I$, $B_R$, $\mu _I$, $\mu _R$.

3 Data analysis

The range of -t covered in this analysis corresponds to a forward region, with |t| from $|t|_\mathrm{min}=0.00074$ GeV$^2$ for T8 to $|t|_\mathrm{max}=0.3709$ GeV$^2$ for T7. In this range the Coulomb effects play an important role and the relative Coulomb phase is taken into account. We compare results for the relative phase $\phi =\phi _\mathrm{{ff}}$, calculated in Appendix A with proton form factor (ff) and the reference case of phase zero $\phi =\phi _{0}=0$. This alternative is examined to set reference values because of a possible lack of understanding of electromagnetic effects, as in the calculation of the phase and the possible influence of the proton radius at high energies.

The statistical methods used in the analyses are performed with CERN-ROOT software [27], accounting for statistical and systematics uncertainties. However, since the values of $\chi ^2$ do not change much compared with the statistical uncertainties only, we understand that the statistical errors are sufficient for the analyses with our amplitudes.

We also study the correlation between the parameters, which is an useful tool to control possible instabilities of the fits. The correlations between the parameters are defined as

$$\begin{aligned} \mathrm{corr}(\alpha ,\beta )=\frac{\langle \alpha \beta \rangle -\langle \alpha \rangle \langle \beta \rangle }{\sqrt{\sigma _{\alpha }^2\sigma _{\beta }^2}}, \end{aligned}$$

(15)

where $\alpha$ and $\beta$ are any two parameters, the brackets are the expectation values of the fitted parameters and $\sigma _\alpha$ and $\sigma _\beta$ the variances associated with them. This correlation criterion is known as the Pearson coefficient and it varies from $-\,1$ to 1, where $-\,1$ is a complete anti-correlation, meaning that if one parameter is increased the other one decreases, and 1 is a complete correlation which means that if one parameter is increased the other one also increases. If the correlation coefficient is zero the parameters are said to be non-correlated, or independent. The correlation factors help us to understand the relation between the determination of the parameter and the range of |t| where this determination is performed.

Table 2 Results of fits for the four datasets. Under Condition (I) all (six) parameters are free. Under Conditions (II), (III) and (IV) the parameters $\rho$ and $\mu _I$ are restricted, as specified in the table. In all cases comparison is made with results obtained with Coulomb–Nuclear interference phase $\phi$ put equal to zero ($\phi _0=0$) and calculated with electromagnetic proton form factor ($\phi =\phi _\mathrm{{ff}}$) as described in Appendix A

With the purpose of identifying generic or universal values for parameters, for all measurements we study four different conditions in the fit:

• (I) all six parameters are free;

• (II) fixing $\rho$ at 0.14, as suggested by dispersion relations;

• (III) fixing $\mu _I$ from the expected positions of imaginary zero [7, 8] and dip in $\mathrm{d}\sigma /\mathrm{d}t$;

• (IV) fixing simultaneously $\rho$ and $\mu _I$ at the above values.

We present our analysis for the four experiments separately in the next subsections. Since T8 has more precise data in the very forward region and the experimental paper has provided a detailed description of the observed structure, we investigate it in more detail. For this purpose we introduce a new diagram to represent the structure in the data at low |t|, plotting the ratio $T_R^2/T_I^2$ against |t|, with

$$\begin{aligned} \frac{T_R^2}{T_I^2}=\frac{(\rho -\mu _R t)^2}{(1-\mu _I t)^2} ~ e^{(B_R-B_I)t} ~. \end{aligned}$$

(16)

This ratio does not depend on the total cross section, and therefore normalization uncertainties are canceled, allowing for identification of the zero in the real amplitude.

The results of the analysis are presented in Table 2. The headings of the table indicate the quantities determined in fits, namely the six parameters $\sigma$,$\rho$,$B_I$,$B_R$, $\mu _I$ and $\mu _R$. The other columns give the derived quantities $t_R$ and $B_I^\mathrm{eff}$, and the estimated $\chi ^2$ values. The first three columns specify the measurement, with the number N of data points, and the phase option (either the true phase $\phi _\mathrm{{ff}}$ or the reference option of zero phase).

3.1 T8

The T8 dataset contains measurements with two different optics. The first set of data (30 points) covers a very forward region, $0.000741< -t <0.191~ \text{ GeV }^2$, and the second set (30 points) starts a bit later, $0.0285< -t < 0.195 ~ \text{ GeV }^2$, overlapping partially with the first, but with better statistical precision. They analyzed separately the first set, here called SET I, with 30 points, and the combination of the first and the second measurements, with $N=60$ points, here called SET II. Analyzing SET I they obtained $\rho =0.12\pm 0.03$. In the analysis with SET II, $\rho$ was not independently determined, but it was rather fixed at the same value of SET I.

Repeating this analysis in two steps, using our nuclear amplitudes and testing phase values $\phi =\phi _0=0$ and $\phi =\phi _\mathrm{{ff}}$, we find that the determination of the $\rho$ parameter is critical, strongly influenced by points in the most forward region. Using Condition (I), with all six parameters free, the results are the following. With SET I we obtain $\rho =0.106\pm 0.021$ for $\phi _\mathrm{{ff}}$ case, which is a little bit below the expectation 0.14 from dispersion relations With the zero reference phase $\phi _0$ we obtain $\rho =0.133\pm 0.021$. With the complete SET II the $\rho$ values come out considerably smaller than in SET-I for both $\phi _0$ and $\phi _\mathrm{{ff}}$ phases, deviating still more strongly from 0.14. These results show the difficulty of T8 for free independent determination of the parameter $\rho$.

SET II is used in the description that follows, and the resulting parameters are registered in Table 2.

Using Condition (I) we obtain equivalent $\mu _R = -2.78$ GeV$^{-2}$ for both $\phi _\mathrm{{ff}}$ and $\Phi _{0}$ phases, but since the values of $\rho$ are different the position of the zero $t_{R}=\rho /\mu _R$ changes from $-\,0.032 \pm 0.004$ to $-\,0.040 \pm 0.004$ GeV$^{2}$ for the $\phi _\mathrm{{ff}}$ and $\phi _{0}$ phases, respectively. We remark that precise data in the vicinity of the zero is important for the determination of $\rho$.

Fig. 1

Result of the T8 data $\mathrm{d}\sigma /\mathrm{d}t$ fit (left) and the corresponding real and imaginary amplitudes (right)

Fig. 2

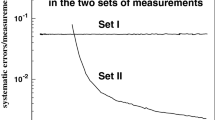
The left plot shows the non-exponential behavior of the differential cross section for T8. The figure is obtained subtracting from the best fit of the differential cross section a reference function which is $\mathrm{d}\sigma /\mathrm{d}t$ written with a pure exponential form and dividing the subtraction by this reference function. The dashed lines show the normalization error band in $\mathrm{d}\sigma /\mathrm{d}t$, which is quite large. The plot in the RHS shows the ratio $T_R^2/T_I^2$, which exhibits information of a non-exponential behavior with advantages compared with the first plot, since $\sigma$ is canceled, and with it most of normalization systematic error, and the second advantage is the clear indication of the structure of the real amplitude showing the position of its zero $|t|_R$

In Fig. 1 we present the fit results of the T8 data with all parameters free, as under Condition I, and phase $\phi _\mathrm{{ff}}$. The parametrization is able to describe the T8 measurements. With plots showing local displacements, shown in Fig. 2, we are able to exhibit details of the structure of the amplitudes. In the LHS we plot a diagram similar to that presented by the experimental group [3], showing the valley structure appearing when we subtract the simple exponential form

$$\begin{aligned} \mathrm{ref} ~= ~A ~ e^{Bt} \end{aligned}$$

from the best fit solution for the differential cross section. The structure appears neatly, but the band of normalization errors is very large, and the roles played by the amplitudes are not clear. In the right hand side of Fig. 2 the quantity $T_R^2/T_I^2$ shows the turning point due to the zero of the real part of the amplitude, with a much narrower band of the systematic errors due to the cancellation of $\sigma$ dependence in the ratio.

The interplay of the magnitudes of the real and imaginary amplitudes influences the structure of $\mathrm{d}\sigma /\mathrm{d}t$. The deviation of a pure exponential behavior is inherent to the sum of two independent squared quantities.

From the fits performed in T8 we obtain from the correlation coefficients that $\rho$ is weakly correlated with all other parameters. This is the reason why, when we fix its value according to Conditions (II) and (IV), we obtain a value of $\chi ^2$ larger than with Condition (I): the other parameters are not able to compensate for the change in $\rho$.

Under both Conditions (I) and (II) the parameter of the imaginary part $\mu _I$ is very small, which means that the t-range in the data is not far enough to feel the zero of the imaginary amplitude. On the other hand, fixing $\mu _I$ under Condition (III), $\rho$ is seen as strongly dependent on the phase.

It is important that, although the parameter $\mu _I$ has low Pearson coefficients, the statistical error associated with this parameter is large, which means that it cannot be well determined with Condition (I) or (II). The $\chi ^2$ values do not change considerably from Condition (I) to Condition (III), but the parameters $B_I$, $B_R$ and $\mu _R$ change. The presence of non-zero negative $\mu _I$ forces the imaginary amplitude to point towards zero. The real amplitude must compensate for the decrease of the imaginary part, reducing the magnitude of the real slope, and the value of $\mu _R$ is also affected. The imaginary slope compensates for the increase in the magnitude of $\mu _I$ introduced in (III), thus preserving the value of $B_I^\mathrm{{eff}}$.

Fig. 3

Correlation maps of the parameters of the real part for T8 measurements under Condition (III)). The flattening behavior of the curves relating $(B_R, \rho )$ and $(\mu _R, \rho )$ show the weak correlation between parameters. The narrow areas in $(B_R, \mu _R )$ indicate the strong correlation between these two parameters

Figure 3 shows the correlation maps between pairs of parameters. These figures correspond to Pearson coefficients $\mathrm{corr} (B_R,\rho )=0.26$, $\mathrm{corr} (\mu _R,\rho )=-0.39$ and $\mathrm{corr} (B_R, \mu _R)=-0.98$ showing weak correlations for the first two cases, and a strong anti-correlation for the latter. The lines represent the allowed regions at different standard deviations. Since $\rho$ is weakly correlated with the parameters of the real part according to Condition (III), under Condition (IV) we expect small deviation in $B_R$ and $\mu _R$. Under this condition we obtain very similar results for the free parameters for both choices of phase.

3.2 A8

In A8 [5] the Atlas Collaboration measured 39 points in the region $0.0105<-t < 0.3635 ~( \text{ GeV }^2)$. With Condition (I) we obtain central $\rho$ values compatible with the dispersion relations (namely 0.14), but with large error bars of 70$\%$. Showing insensitivity, the values of $\mu _R$ are similar for $\phi _\mathrm{{ff}}$ and $\phi _{0}$ phases. Although the $\mu _R$ values in A8 and T8 are different by 20%, the positions of the real zero differs about 6%. The real amplitudes for T8 and A8 are shown in Fig. 4 and we can clearly note that the position of the Martin zero is in agreement between the measurements.

Fig. 4

Comparison of the real amplitudes in T8 (solid lines) and A8 (dashed lines) measurements. These amplitudes represent Condition (I), with all parameters free and phase $\phi _\mathrm{{ff}}$. The (almost) coincidence of the zeros in T8 and A8 is remarkable

Important differences between T8 and A8 are in the parameters of the imaginary part. Thus $\mu _I=-1.65 \text{ GeV }^{-2}$ for A8, while for T8 it is compatible with the zero due to the short |t| range of the data.

The values of $\sigma$ in A8 and T8 differ by $\sim 5\%$. This difference may be due relative normalization, and we may wonder whether a unification of $\mathrm{d}\sigma /\mathrm{d}t$ through a constant factor could unify the solutions for $\sigma$, while leading also $\rho$ and $\mu _R$ to common values.

Since the fits for A8 show a strong anti-correlation factor between $\sigma$ and $\rho$, and $\sigma$ is a stable parameter, we use Condition (II) to fix $\rho$ at 0.14 and obtain a value of $\chi ^2$ very similar to the result obtained under Condition (I) with free $\rho$, which is natural since in (I) $\rho$ in not very different from 0.14. Under Condition (II), with fixed $\rho$, the results for T8 and A8 give compatible $\mu _R$ values.

In A8, for both (I) and (II), the $\mu _I$ parameter predicts $|t_I|=0.59 \text{ GeV }^{2}$, which is far on the right of the region where the dip in $\mathrm{d}\sigma /\mathrm{d}t$ is expected to occur. By fixing $\mu _I$ in Condition (III), $B_I$ for A8 agrees with the value found in T8, as expected, since values of $B_I^\mathrm{{eff}}$ are in agreement for all conditions.

The use of Condition (IV) does not change considerably the parameters of A8 when compared with Condition (III), because the central values of $\rho$ in (III) are close to 0.14.

3.3 T7

At $\sqrt{s}=7$ TeV the Totem Collaboration measured elastic p-p cross sections with two sets [1], the first in the range ($0.005149< -t< 0.3709$ GeV$^{2}$ ) with 87 points, and the second in the range $0.377< -t< 2.443$ GeV$^{2}$ with 78 points. Using our expressions for the forward amplitudes, we analyze the forward set, obtaining the results shown in Table 2. With all parameters free, for both $\phi _\mathrm{{ff}}$ and $\phi _0$ phases the $\rho$ values are less than 0.14. The values for $\mu _I$ are similar to those in A8. The total cross section is higher but compatible with the original paper [1], as given in Table 1.

The correlation factor $\mathrm{corr} (\sigma ,\rho )=-0.95$ obtained under Condition (I), shows a strong anti-correlation. Since $\sigma$ is a stable parameter and the central $\rho$ value is larger than the expected 0.14, Condition (II) fixing $\rho$, leads for all other parameters and for $\chi ^2$ results similar to Condition (I).

With Condition (III) we observe that the central $\rho$ values are smaller than obtained with (I), and the statistical errors are about 55$\%$ ($\phi _0$) and 88$\%$ ($\phi _\mathrm{{ff}}$) of the central value.

Analysis of an extended set

Table 3 Fits for the extended T7 data ($N=104$ points in the range $0.00515< -t< 0.52 ~ \text{ GeV }^2$) according to Conditions (I), (II) and (IV)

The special availability in T7 of data beyond the $|t| \approx 0.4 \text{ GeV }^2$ limit of the measurements in Table 1, may be used to study a range where the $\mu _I$ parameter becomes more effective, pointing towards the zero of the imaginary amplitude, and being determined with higher accuracy. We thus add to the forward set the first 17 points of the second dataset, reaching $|t_\mathrm{max}|=0.52 \text{ GeV }^2$. The results of the analysis with the combined set of 104 points are presented in the Table 3.

The study of the extended set with Condition (I) leads to the correlation map for the quantities $B_I$ and $\mu _I$ shown in Fig. 5. The Pearson coefficient depends on the range on t where the fit is made and of course the fit conditions used, and for this extended range it shows a slight anti-correlation between $\mu _I$ and $B_I$.

In Fig. 6 we compare the squared magnitudes of the real and imaginary amplitudes, and also the simplified single exponential amplitude assuming the effective slope $B_I^\mathrm{eff}$, for the extended T7 with Condition (I). We observe that the imaginary part starts to deviate from the simple exponential near $|t|\sim 0.2$ GeV$^2$, and at $|t|\sim 0.47$ GeV$^2$ it passes through a zero. Beyond this range the real amplitude would be modified to incorporate other terms (say a quadratic $\xi _R t^2$) that may play an important role in the construction of the dip structure.

As with the forward set, here the $\rho$ values come out larger than 0.14, but within error bars. Fixing $\rho =0.14$ under Condition (II), the changes in parameters and in $\chi ^2$ are very small.

It is very important that the parameter $\mu _I$ is here determined with more precision and is compatible with the value fixed to establish Condition (III) in Table 2.

The use of Condition (IV) for this extended set, shown in Table 3, leads to a decrease in the magnitudes of $B_R$ and $\mu _R$ when we compare with the results of the forward set under the same condition. Since $\rho$ is fixed, the decrease in $\mu _R$ implies an increase in the magnitude of $|t_R|$.

Fig. 5

Correlation map between the parameters $B_I$ and $\mu _I$ for the extended T7 set (104 points) studied under Condition (I)

Fig. 6

Comparison of the squared magnitudes of real, imaginary and simplified single exponential amplitudes for the extended T7 dataset, with 104 experimental points (full circles). The real amplitude has a zero near 0.04 $\text{ GeV }^2$ and its magnitude competes with the imaginary amplitude from $|t|=0.3$ GeV$^2$. The imaginary amplitude deviates from simple exponential form near $|t|\sim 0.2$ GeV$^2$ and passes through zero at $|t|=0.47$ GeV$^2$

3.4 A7

In A7 the Atlas Collaboration measured [2] 40 points in the region $0.0062<-t < 0.3636 ~( \text{ GeV }^2)$. This experiment is challenging, since the experimental authors recognize that $\rho$ cannot be determined from the data with usual forms of amplitudes. The natural result for $\rho$ as a free parameter is a negative quantity, and we run Condition (I) imposing a lower bound 0 for $\rho$, and of course the expected value is zero, with large error bars. Under this condition the total cross section for $\phi _\mathrm{{ff}}$ phase is $\sigma = 95.77$ mb, which is well below, while the parameters $B_I$, $B_R$, $\mu _R$ and $\mu _I$ are compatible with T7. In these measurements the correlation factors between $\rho$ and all other parameters are very small. Thus with Condition (II) we expect an obvious increase of $\chi ^2$, but the parameters $B_I$, $B_R$ and $\mu _R$ are compatible with T7.

With Condition (I), $\mu _I$ is compatible with zero, with large error. With Condition (III), $\chi ^2$ is not much changed, as well as the total cross section. The $\rho$ value is still undetermined but $B_I$, $B_R$ and $\mu _R$ are compatible with the other experiments. Thus, in spite of the smaller value of total cross section and instabilities in the determination of $\rho$, Condition (IV) shows a similar t dependence in A7 with respect to the other datasets, with a similar behavior of the amplitudes.

4 Summary of the analysis

The LHC measurements at $\sqrt{s}$ = 7 and 8 TeV shown in Table 2 are analyzed under the assumption of the analytical forms for the scattering amplitudes given in Eqs. (4) and (6). These forms are considered to be as simple as possible under theoretical conditions to describe the scattering amplitudes in the forward region. The analysis aims at the determination of six intervening parameters, three for the imaginary part ($\sigma$, $B_I$, $\mu _I$) and three ($\rho$, $B_R$, $\mu _R$) for the real part, with expected smooth energy dependence. Only the T8 measurements cover the very small |t| range, so that the analysis is made with non-homogeneous inputs, and four specific conditions, named (I), (II), (III), (IV) in Table 2, are studied separately.

The Coulomb–Nuclear interference is a crucial ingredient, and its phase $\phi _\mathrm{{ff}}$ is treated compatibly with the forms of the amplitudes, as presented in Appendix A. In order to have a reference (although it is not realistic) we also give results of fits with phase $\phi _0$ put equal to zero.

As expected, the direct results of the fits with all parameters kept free are rather dispersive in some aspects, as shown in the sub-table with title Condition (I). The fitted values of $\rho$ do not agree among the measurements within the statistical uncertainties, but once the normalization uncertainty is considered, the values are in agreement. We observe that the other parameters of the real part ($B_R$ and $\mu _R$), related to the shape of the amplitudes but not so strongly to its normalization, appear to be more regular.

Under Condition (II) $\rho$ is fixed at a reference value 0.14 suggested by dispersion relations for the 7–8 TeV range. Compared to (I) there is a loss in $\chi ^2$ in the cases with free $\rho$ far from 0.14, namely T8 and A7, but not in the other cases, where we observe only a rather slight adaptation in the other real parameters: $B_R$ and $\mu _R$ appear as regular quantities. Also $B_I$ remains the same (except in A7), and it is particularly important to remark that the effective slope $B_I^\mathrm{eff}=B_I-2 \mu _I$ in Eq. (12), which compensates for the influence of $\mu _I$ on the |t| dependence of the imaginary part, appears as a very regular common quantity. In spite of the differences, at this point we may say that we are lead accept the value $\rho \approx 0.14$ for all measurements. On the other hand, $\mu _I$ does not remain regular among the experiments under this Condition (II). Since $\mu _I$ is responsible for the presence of a zero ($t_I=1/\mu _I$) in the imaginary amplitude (which occurs near the dip in $\mathrm{d}\sigma /\mathrm{d}t$ at about 0.4 $\text{ GeV }^2$), it is natural that T8 (limited to 0.2 $\text{ GeV }^2$) is not sensitive to $\mu _I$, and puts it at zero under Conditions (I) and (II).

It is interesting to observe the effects of correlations. For instance, in T8 and A7, $\rho$ is weakly correlated with the other parameters. Then fixing $\rho$ under Condition (II) worsens strongly $\chi ^2$ for these datasets, more than in sets A8 and T7 where the strong correlation between $\rho$ and the other parameters absorb the effects of the fixing condition. For T8 in the $\phi _\mathrm{{ff}}$ case the worsening in $\chi ^2$ is more dramatic, corroborating our concern about proton form factor and Coulomb phase.

With Condition (III) we fix $\mu _I$ according with the expected positions of the imaginary zero and dip in $\mathrm{d}\sigma /\mathrm{d}t$ [7, 8], and let $\rho$ free. This is successful, as $\rho$ results about the same or improved with respect to Condition (I) (all parameters free), except for A7, as expected. The parameters $B_R$ and $\mu _R$ of the real part remain the same, and it is remarkable that $B_I$ changes, becoming very regular, absorbing the influence of $\mu _I$ (now fixed) and keeping the constant and regular effective |t| dependence of the imaginary amplitude, represented by $B_I^\mathrm{eff}$.

The $\mu _I$ parameter determines a zero at $t_I=1/\mu _I$ in the imaginary amplitude and is related with the position of the dip in the differential cross section. A precise determination of $\mu _I$ depends on the existence of data in a region near the dip. Thus in the T8 dataset, without points for small |t|, the central values of $\mu _I$ are near zero in (I) and (II), while in A8, T7 and A7 the values have larger magnitudes. We study this question analyzing the T7 experiment with inclusion of a second set of points [1]. Forming a larger dataset in the range 0.005149–0.52 $\text{ GeV }^2$, the best solution with fixed $\rho =0.14$ gives $\mu _I=-2.15~ \text{ GeV }^{-2}$ shown in Table 3, in good agreement with the prediction [8]. We are thus lead to Conditions (III) and (IV), which fix $\mu _I$.

Fixing both $\rho$ and $\mu _I$ at their expected values under Condition (IV) we obtain good modeling for all measurements, except for the total cross sections, which separate Atlas from Totem. It is particularly significant that the position of the zero of the real amplitude is nearly the same for all cases.

The deviation from pure exponential form in the differential cross section is interpreted as due to the shape difference between the real and imaginary amplitudes. The T8 experiment presents very precise data at low |t|, showing a valley behavior in the differential cross section, while the T7, A7 and A8 data also indicate a structure for the data at low |t|, but with large uncertainties. The shape is constructed when the real amplitude crosses zero, passing to negative values. After the zero, the action of the real slope pushes this negative value back to zero, and the structure is formed.

This mechanism suggests that the determination of $\rho$ depends not only on the extrapolation to the limit at $|t|=0$, but that it also depends on the form of the real amplitude around its zero. A precise extraction of $\rho$ depends both on the specific analytical model used and on the data in the whole range $0<-t<0.2$ GeV$^2$ where the valley occurs. The position of the real zero is obtained from the equation $t_{R}=\rho /\mu _{R}$ (values are given in Table 2).

Important quantities are the derivatives of the amplitudes and their effective slopes determined in each measurement. The exponent $B_I$ written in Eq. (4) is not the logarithmic derivative of the imaginary amplitude, which is given by Eq. (12). The effective slope at small |t|,

$$\begin{aligned} B_{I}^\mathrm{eff}\simeq B_I-2\mu _I , \end{aligned}$$

is seen in the approximation of the linear factor put in exponential form $1-\mu _I t \approx \exp (-\mu _I t)$. Thus the determinations of $\mu _I$ and $B_I$ depend on data in the very forward region, and also in the region near the dip. Table 2 shows the interesting regularity of the quantity $B_I^\mathrm{eff}$, as opposed to $B_I$.

The average slope B measured in the differential cross section is given in Eq. (14). In our analysis B appears to be stable, with a value $B\simeq 20.5$ GeV$^{-2}$. Comparing our result with the values in Table 1 we see deviations of about 1 GeV$^{-2}$, and we thus remark that the measured average slope B depends on the parameters $\mu _I$ and $\mu _R$, which are influenced by data in the large |t| region.

The quality of the representations of the data can be read from the pull plots in Fig. 7. The y-axis represents the standard deviations at each |t| and is defined as $(\mathrm{d}\sigma /\mathrm{d}t_\mathrm{exp}^{i}$-$\mathrm{d}\sigma /\mathrm{d}t_\mathrm{the}(t_i) )/ \mathrm{er}_i$, where $\mathrm{d}\sigma /\mathrm{d}t_\mathrm{exp}^{i}$ is the experimental value at some $t_i$ with error $\mathrm{er}_i$, and $\mathrm{d}\sigma /\mathrm{d}t_\mathrm{the}(t_i)$ is the theoretical value calculated at $t_i$. Assuming that the statistical errors follow Gaussian distributions, the most probable solution should contain about 68$\%$ of the points within $\pm 1 \sigma$ (deviation) and about 95$\%$ of the points within $\pm 2 \sigma$. For T8 we see that about 65$\%$ of the points are within $\pm 1 \sigma$ following this criterion, and for A8 about 74$\%$ of the points are within $\pm 1 \sigma$. Of course, care should be taken in this analysis because a large number of experimental points are needed for good statistics.

For T7, about 65$\%$ of the experimental points are within $\pm 1 \sigma$ and about 94$\%$ within $\pm 2 \sigma$ of deviation with respect to the theoretical curve (fitted curve). Since these are the measurements with larger number of points (N=87), the maximum likelihood criterion for Gaussian statistical errors shows that our curve is a good representation of the data.

Fig. 7

Pull plots of the analysis of the measurements. The y axis in a pull plot is defined as $(\mathrm{d}\sigma /\mathrm{d}t_\mathrm{exp}^{i}$-$\mathrm{d}\sigma /\mathrm{d}t_\mathrm{the}(t_i) )/ \mathrm{error}_i$, where $\mathrm{d}\sigma /\mathrm{d}t_\mathrm{exp}^{i}$ is the experimental value at some $t_i$ with $\mathrm{error}_i$ and $\mathrm{d}\sigma /\mathrm{d}t_\mathrm{the}(t_i)$ is the theoretical value calculated at $t_i$. According to the maximum likelihood criterion (assuming statistical errors following Gaussian distributions) the best descriptions of the data are concentrated in T8 and T7 experiments where about 68$\%$ of the experimental points are within 1 sigma deviation from the model

The regularity on the values of $\mu _R$ is remarkable. The zero of the real part $t_R$ determined by the parameters $\mu _R$ and $\rho$ is associated with the predicted zero of the theorem by Martin [6]. We see that the position of the zero is stable in all experiments and in Table 4 we observe agreement at $t_R\simeq -0.037$ GeV$^{2}$ within the statistical errors. In terms of amplitudes we observe that the position of the zero together with the magnitude of $B_R$ determines the structure shown in Fig. 2. The existence of this zero is very important for the superposition of the real and imaginary parts that controls the detailed structure of $\mathrm{d}\sigma /\mathrm{d}t$ in the low |t| region.

Finally, as a general remark we observe that total cross sections maintain that Totem values are higher than Atlas by 4–6 mb (about 5%), and the numbers remain stable under all conditions studied. The difference is not due to statistical fluctuation, but rather it is related to normalization procedures, both experiments informing a relatively high systematic uncertainty. Using Condition (I), we observe at 8 TeV

$$\begin{aligned} \sigma (T8)=102.7 \pm 0.07 (\mathrm{stat}) \pm 2.2 (\mathrm{syst}), \end{aligned}$$

$$\begin{aligned} \sigma (A8)= 97.02 \pm 0.52 (\mathrm{stat}) \pm 2.4 (\mathrm{syst}), \end{aligned}$$

and then

$$\begin{aligned} \sigma (T8)-\sigma (A8) = 5.7 \pm 0.5 (\mathrm{stat}) \pm 3.3 (\mathrm{syst}). \end{aligned}$$

Therefore, in our proposed model the discrepancy between the two measurements is less than 2 standard deviations. As another check, we observe that under Condition IV the systematic differences in $\sigma$ do not affect the other parameters, which are all coherent.

Another general remark is that differences in the results obtained with the two assumptions for the Coulomb phase are relevant only for T8 that has experimental points for very small |t|. It may be fortuitous, but we observe that $\chi ^2$ is smaller when the phase is put at $\phi _0=0$.

The difficulty in the determination of $\rho$ may be due to Coulomb–Nuclear interference. The distribution of electric charge in the proton determined by electromagnetic scattering at low energies ($\Lambda ^2=0.71~ \text{ GeV }^2$) may be unrealistic for high energy hadronic scattering. In Appendix A we show that with expanded proton size (as may be the case at high energies) the Coulomb phase decreases. We see that the problem of the Coulomb interference in elastic pp scattering still has open questions.

5 Conclusions

In this work we study the properties of the amplitudes in pp elastic scattering analyzing experimental data at the LHC center-of-mass energies 7 and 8 TeV, based on a model for the complex amplitude, with explicit real and imaginary parts, each containing an exponential slope and a linear factor to account for the existence of a zero. The zero of the real part, close to the origin, corresponds to Martin’s theorem, and the zero of the imaginary part anticipates the dip in the differential cross section that occurs beyond the range of the available data under study.

Our study shows that the real amplitude plays crucial role in the description of the differential cross section in the forward region. Interference with the Coulomb interaction is properly accounted for, and use is made of information from external sources, such as dispersion relations and predictions for the imaginary zero obtained in studies of full-t behavior of the differential cross section [7, 8]. We organize the analysis under four conditions, according to the specifications of the parameters with values fixed in each case. Comparison is made of the results obtained for the four experimental measurements. We obtain the results shown in Table 4, which we believe to be a good representation of the experimental data of Table 1.

Table 4 Proposed values of parameters for the four datasets. The phase of the Coulomb interference is calculated with electromagnetic proton form factor as described in Appendix A. The T7 data are also shown with inclusion of points at higher |t| that are important for confirmation of the value of $\mu _I$

Assuming $\sigma \sim \log ^2{s}$ at high energies, dispersion relations give $\rho \sim \pi /\log s$, and we know that the position of the first real zero [8] behaves like $|t_R| \simeq A+1/(c_0+c_1\log {s}+c_2\log ^2{s})$. From Eq. (11) it then follows that $\mu _R$ increases like $- \lambda \log {s}$ at high energies. With s in $\text{ GeV }^2$, from Table 4 we obtain $\lambda \simeq 0.2 ~ \text{ GeV }^{-2}$. Future precise measurements in LHC at 13 TeV may be investigated with this purpose. Our present work predicts that the zero at $\sqrt{s}= 13$ TeV is at $t_R=-0.037 \text{ GeV }^2$.

The quantity $\mu _R$ is related with the scaling variable $\tau = t \log ^2{s}$ introduced by Dias de Deus [28, 29] connecting s and t dependences in the amplitudes at high energies and small |t|. Martin [30] uses the same idea of a scaling variable, writing an equation for the real part $\rho (s,t)$ using crossing symmetric scattering amplitudes of a complex s variable, valid in a forward range. The proposed ratio is

$$\begin{aligned} \rho (s,t)\simeq \frac{\pi }{\log s}\Big (1+\frac{\tau (\mathrm{d}f(\tau )/\mathrm{d}\tau )}{f(\tau )}\Big ), \end{aligned}$$

(17)

where $f(\tau )$ is a damping function, with the implicit existence of a real zero. The form of $f(\tau )$ determines the properties of the real zero [31], found in the analysis of the data. This may be a clue for the introduction of explicit crossing symmetry and analyticity in our phenomenological treatment of the data.

Other models [9,10,11,12,13,14,15,16] also deal with the position of the real zero, discussing different analytical forms for the amplitudes, and it would be interesting to have their predictions for the amplitudes in the forward range.

In Appendix B we investigate the behavior the amplitudes in b-space for a geometric insight of the scattering process. We find that although our amplitudes never violate Eq. (B11) up to $\sqrt{s} =$ 8 TeV at LHC, the differential cross sections in b-space are all monotonically decreasing functions in b. This means that our amplitudes do not indicate any signal for peripheral dominant elastic scattering process. However, in an analysis of T8 the dominance of the square of the real amplitude in b-space in Ref. [32] was interpreted as peripheral behavior. To settle this interesting question, data at larger |t| are required.

In non-perturbative QCD, in several instances, the proton appears as a structure with expanding size as the energy increases [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47], with varied mechanisms, as distribution of valence quarks in a cloud around a core, modifications in QCD vacuum in the region of the colliding particles, and so on. Together with the evolution of the proton hadronic size, its electromagnetic properties, as they appear in high energy collisions, may change also. A linear increase in $\log {s}$ is a usual assumption for the effective proton radius, and the form-factor parameter $\Lambda ^2$ would then be reduced by about 1/2, corresponding to an increase of about 40 % in the proton radius. In Appendix A we calculate the interference phase with this example.

We expect that future data in pp elastic scattering at 13 TeV and higher energies will have a high quality, covering a wide t range to allow for a determination of the properties of the real and imaginary amplitudes in pp elastic scattering, including studies of the amplitudes up to the perturbative tail of large |t|. Hopefully the experimental groups will receive the necessary support and encouragement for this effort.

Appendices

Appendix A: Coulomb phase

We study the phase of t scattering according to the formulation based on superposition of nuclear and Coulomb interactions in the eikonal formalism. The expressions for the phase accounting for the structure of the real and imaginary parts of the amplitude are obtained.

The Coulomb interference in pp elastic scattering is very important for the analysis of LHC experiments, where the properties of the amplitudes are investigated. The phase $\phi$ of the quantum interference between Coulomb and nuclear interactions was studied by several authors [7, 20,21,22,23,24,25,26]. A first approach for the so-called Coulomb phase is the point-like (pure Coulomb) phase, derived by West Yennie [22, 23] calculated in the context of quantum field theory, considering the nuclear imaginary and real amplitudes with the same t dependence and a proton with zero radius. The results for a point-like proton [22, 23] have been generalized [7] allowing for different slopes for the real and imaginary nuclear amplitudes. A second approach is the form-factor phase, which considers an eikonal treatment for the superposition of amplitudes and a geometrical size with a form factor for the proton structure [20, 21, 24, 25].

The expression for the phase depends on the analytical structure of the real and imaginary parts of the nuclear amplitude. Here we derive in the same eikonal formalism an expression for the Coulomb interference phase appropriate for forward scattering amplitude with t dependence of the form

$$\begin{aligned} T^N(t)= & {} \frac{\sigma }{4\sqrt{\pi }(\hbar c)^2}\Big [\big (\rho _R-\mu _R t -\xi _R t^2\big )e^{B_R t/2} \nonumber \\&+ \, i \big (\rho _I-\mu _I t -\xi _I t^2 \big )e^{B_I t/2}\Big ] ~, \end{aligned}$$

(A1)

which is assumed to be realistic for the description of $\mathrm{d}\sigma /\mathrm{d}t$ data for high energy, satisfying the expected properties concerning zeros, signs and magnitudes of the amplitudes in the forward range. To have systematic symmetry in the notation, we write $\rho _R=\rho$ for the usual $\rho$ parameter, and $\rho _I=1$.

The usual dipole electromagnetic form factor is

$$\begin{aligned} f(q^2)=\Big (\frac{\Lambda ^2}{q^2+\Lambda ^2}\Big )^2~, \end{aligned}$$

(A2)

with $\Lambda ^2=0.71 \text{ GeV }^2$. To simplify our calculations, we may alternatively use the Gaussian representation for the form factor

$$\begin{aligned} f(q^2)=e^{-2q^2/\Lambda ^2}~, \end{aligned}$$

(A3)

trusting that differences in results for the phases are unimportant, as confirmed by Cahn [24].

The Coulomb amplitude for pp scattering, written

$$\begin{aligned} F^C(s,q^2)=-\frac{\alpha s}{(q^2)} f^2(q^2), \end{aligned}$$

(A4)

enters the Coulomb–Nuclear Interference (CNI) in the form

$$\begin{aligned} F^{N+C}(s,q^2)=-\frac{\alpha s}{(q^2)} f^2(q^2) ~ e^{i\alpha \phi } + F^N(s,q^2) \end{aligned}$$

(A5)

with normalization defined by

$$\begin{aligned}&\sigma =\frac{4 \pi }{s} \mathrm{Im}~ F^N(q=0) ~ , \nonumber \\&- \frac{\mathrm{d} \sigma }{\mathrm{d}q^2}= \frac{\pi }{s^2} |F|^2. \end{aligned}$$

(A6)

The correspondence between the dimensionless nuclear amplitude $F^N$ and the phenomenological $T^N$ is given by

$$\begin{aligned} T^N(s,t)=\frac{\sqrt{\pi }}{(\hbar c)^2}\frac{F^N(s,q^2)}{s}~. \end{aligned}$$

(A7)

We start from the exact expression for the phase

$$\begin{aligned}&\phi (s,-q^2)\nonumber \\&= {\mp } \int _0^{\infty }\mathrm{d}^2\mathbf{{q'}}\ln \Big (\frac{q'^2}{q^2}\Big )\frac{\mathrm{d}}{\mathrm{d}q'^2} \left[ f^2(q'^2)\frac{F_N(s,[\mathbf{{q}}-\mathbf{{q'}}]^2)}{F_N(s,q^2)}\right] , \nonumber \\ \end{aligned}$$

(A8)

the signs ${\mp }$ corresponding to the ${\mathrm{pp}}/{\mathrm{p}}{\bar{\mathrm{p}}}$ systems.

Cahn has considered the approximation

$$\begin{aligned}&(1/(2\pi )) \int _0^{2\pi }\mathrm{d}\theta F_N(s,(\mathbf{q'-q})^2)/F_N(s,q^2) \nonumber \\&\approx F_N(s,(q'^2)/F_N(s,0), \end{aligned}$$

(A9)

justifying that the momentum transfer scale $q^2$ is much smaller than the inverse size of the proton. This is a very strong assumption, which should be tested in specific cases. Following the suggestion, Eq. (A8) becomes

$$\begin{aligned} \phi (s,t)={\mp } \int _0^{\infty }\mathrm{d}t'\ln \Big (\frac{t'}{t}\Big )\frac{\mathrm{d}}{\mathrm{d}t'} \Big [f^2(t')\frac{F_N(s, t')}{F_N(s,0)}\Big ], \nonumber \\ \end{aligned}$$

(A10)

where for simplicity we use the $t'$ variable instead of $q'^2$. As a generalization with respect to Cahn’s calculation, we take for the nuclear amplitude the same expression in Eq. (A1). Then we need to evaluate the integrals

$$\begin{aligned} H_N(t,b_\beta )= & {} \int _0^{-\infty }\mathrm{d}t'\ln \Big (\frac{t'}{t}\Big )~ \frac{\mathrm{d}}{\mathrm{d}t'}\big [t'^N ~ e^{4t'/\Lambda ^2} e^{B_\beta t'/2} \big ] ~ \nonumber \\= & {} \int _0^{-\infty }\mathrm{d}t'\ln \Big (\frac{t'}{t}\Big )~\frac{\mathrm{d}}{\mathrm{d}t'}\big [t'^N ~ e^{b_\beta t'}\big ], \end{aligned}$$

(A11)

where we have used the definition

$$\begin{aligned} b_\beta = \frac{4}{\Lambda ^2} +\frac{B_\beta }{2} \end{aligned}$$

(A12)

with $\beta = R, I$.

The results of the integrations ($N=0,1,2$) are

$$\begin{aligned}&H_0=\gamma ~+ ~\log (- b_\beta t), \nonumber \\&H_1= \frac{1}{b_\beta }, \nonumber \\&H_2= - \frac{1}{b_\beta ^2}, \end{aligned}$$

(A13)

where $\gamma =0.5772$ is the Euler gamma constant. The phase is then written

$$\begin{aligned} \phi (s,t)= & {} {\mp } \frac{1}{\rho + i} \bigg \{ \bigg [- \frac{\mu _R}{b_R}+\frac{\xi _R}{b_R^2} + \rho \bigg (\gamma + \log (- b_R t)\bigg ) \bigg ] \nonumber \\&+ \, i ~ \bigg [- \frac{\mu _I}{b_I}+\frac{\xi _I}{b_I^2} + \gamma + \log (- b_I t) \bigg ] \bigg \}, \end{aligned}$$

(A14)

with real and imaginary parts, respectively,

$$\begin{aligned}&\phi _{R} (t)={\mp }\bigg \{\frac{1}{1+\rho ^2} \bigg [ \bigg [- \frac{\mu _I}{b_I}+\frac{\xi _I}{b_I^2}+\log (b_I) \bigg ] \nonumber \\&+ \rho \bigg [ - \frac{\mu _R}{b_R}+\frac{\xi _R}{b_R^2} +\rho ~ \log (b_R)\bigg ] \bigg ]+ \gamma + \log [-t] \bigg \} \end{aligned}$$

(A15)

and

$$\begin{aligned}&\phi _{I} (t)= {\mp } \frac{1}{1+\rho ^2} \bigg \{ \rho \bigg [- \frac{\mu _I}{b_I}+\frac{\xi _I}{b_I^2}+\log ( b_I) \bigg ] \nonumber \\&- \bigg [- \frac{\mu _R}{b_R}+\frac{\xi _R}{b_R^2} + \rho \log ( b_R ) \bigg ] \bigg \}. \end{aligned}$$

(A16)

Equations (A15) and (A16) are our final results for the phase calculated with form factors, in a generalization of the work by Cahn [24], assuming more complete structures for the real and imaginary parts of the scattering amplitude. It may be of practical usefulness to define

$$\begin{aligned} C_R = - \frac{\mu _R}{b_R}+\frac{\xi _R}{b_R^2} + \rho ~ \log ( b_R ) \end{aligned}$$

(A17)

and

$$\begin{aligned} C_I = -\frac{\mu _I}{b_I}+\frac{\xi _I}{b_I^2} +\log ( b_I ) , \end{aligned}$$

(A18)

and then write

$$\begin{aligned} \phi _{R} (t)= {\mp } \bigg [ \frac{1}{1+\rho ^2} \big [ C_I+ \rho ~ C_R \big ] + \gamma + \log (-t) \bigg ] \end{aligned}$$

(A19)

and

$$\begin{aligned} \phi _{I} (t)= {\mp } \frac{1}{1+\rho ^2}\big [\rho ~ C_I-C_R \big ] ~. \end{aligned}$$

(A20)

It must be observed that in these expressions $b_R$, $b_I$ and $-t$ have compatible units, as $\text{ GeV }^{-2}$ and $\text{ GeV }^2$. The result is simple: in the real part the t dependence is purely linear in $\log (-t)$, the imaginary part is a very small constant, and there is no explicit energy dependence.

In the simplified case $\mu _R=\mu _I=0, ~ \xi _R=\xi _I=0, ~ B_R=B_I=B,$

$$\begin{aligned} b_R=b_I=b=\frac{4}{\Lambda ^2}+\frac{B}{2} \end{aligned}$$

we obtain Cahn’s original form.

The real and imaginary parts of the phase are plotted in Fig. 8 with an example of values for the parameters.

Fig. 8

Phase of the Coulomb–Nuclear interference with examples for the values of the parameters. We plot also the phase calculated with $\Lambda ^2=0.71/2 \text{ GeV }^2$

In the figure we plot also a (dot-dashed) line representing the real part of the phase calculated for a larger proton, with $\Lambda ^2=0.305 \text{ GeV }^2$.

Appendix B: b-space properties

The dimensionless Fourier transform with respect to the momentum transfer

$$\begin{aligned} \tilde{T}(s;b)=\tilde{T}_{R}(s;b)+i\tilde{T}_{I}(s;b) \end{aligned}$$

(B1)

of the amplitude T(s, t) in Eqs. (4) and (6) is given by

$$\begin{aligned}&\tilde{T}_{R}\left( s;b\right) \nonumber \\&=\frac{\sigma }{2\pi B_{R}}\Bigg \{ \rho +\frac{\mu _{R}}{B_{R}}\left( 2-\frac{b^{2}}{B_{R}}\right) \Bigg \} e^{-b^{2}/2B_{R}} \end{aligned}$$

(B2)

and

$$\begin{aligned}&\tilde{T}_{I}\left( s;b\right) \nonumber \\&=\frac{\sigma }{2\pi B_{I}}\left\{ 1+\frac{\mu _{I}}{B_{I}}\left( 2-\frac{b^{2}}{B_{I}}\right) \right\} e^{-b^{2}/2B_{I}}. \end{aligned}$$

(B3)

Figure 9, with $\tilde{T}$ at $\sqrt{s}$= 8 TeV as a function of b for T8 and A8, shows the behavior of the amplitudes, which differ by only a few % in the two measurements. We note that the magnitude of real parts become comparable and even larger than the imaginary parts for large b. This behavior, which occurs also for the 7 TeV datasets, is not observed at lower energies.

Fig. 9

b-space amplitudes at 8 TeV. Solid and dashed lines correspond to A8 and T8 measurements, respectively. As seen in the inset in the right-up corner, the real parts cross the imaginary parts around $b\sim 12$ $\mathrm{GeV}^{-1}$ and become dominant for the peripheral region. For 7 TeV the structures are similar

To investigate in more detail the significance of the dominance of the real part in the peripheral region, we introduce the eikonal representation of the b-space amplitude ([8])

$$\begin{aligned} \tilde{T}\left( b,s\right) \equiv i\sqrt{\pi }\left( 1-e^{i\chi \left( s,b\right) }\right) , \end{aligned}$$

(B4)

and the so-called b-space differential cross sections (profile functions) are

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{el}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b}} =1-2\cos \chi _{R}e^{-\chi _{I}}+e^{-2\chi _{I}}, \end{aligned}$$

(B5)

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{tot}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b}}=2\left( 1-\cos \chi _{R}e^{-\chi _{I}}\right) , \end{aligned}$$

(B6)

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{inel}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b} }=1-e^{-2\chi _{I}}, \end{aligned}$$

(B7)

where $\chi _{R}={\text {Re}}\left( \chi \right)$ and $\chi _{I}={\text {Im}}\left( \chi \right)$.

Fig. 10

b-space differential cross sections for $\sqrt{s}$ = 8 TeV, with solid and lines for A8 and T8, respectively. In the whole b domain, the inelastic contribution is by far dominant over the elastic one

These b-space representations of the differential cross sections offer a geometric view of the pp interactions, although such interpretation should be taken with caution, since they are not physical observables. From the unitarity condition of the scattering amplitude, we must have $\chi _I\ge 0$, and $\mathrm{d}\sigma _\mathrm{inel}/\mathrm{d}^2 b \le 1$. For $b> 10 \text{ GeV }^{-1}$ we have $\left| \tilde{T}\right| \ll 1$, which implies $\left| \chi \right| \ll 1$. Thus, in this region, taking up to the leading orders in $\chi _{R}$ and $\chi _{I}$, respectively, we obtain

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{el}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b}}\sim \chi _{_{R}}^{2}=\frac{1}{\pi }\tilde{T}_{R}^{2},\ \ \end{aligned}$$

(B8)

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{tot}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b}} \sim 2\left( \chi _{I}+\frac{1}{2}\chi _{_{R}}^{2}\right) =\frac{2}{\sqrt{\pi } }\tilde{T}_{I}+\frac{1}{\pi }\tilde{T}_{R}^{2}, \end{aligned}$$

(B9)

and

$$\begin{aligned} \frac{\mathrm{d}\tilde{\sigma }_\mathrm{inel}\left( s,\mathbf {b}\right) }{\mathrm{d}^{2}\mathbf {b}} \simeq 2\chi _{I}\simeq \frac{2}{\sqrt{\pi }}\tilde{T}_{I}. \end{aligned}$$

(B10)

From the above, it is clear that in the domain where $\left| \tilde{T}\right| \ll 1$ (that is, where the Born approximation is valid), the inelastic part comes totally from $\tilde{T}_{I}$, while the elastic contribution may exceed the inelastic one if

$$\begin{aligned} \tilde{T}_{R}^{2}>2\sqrt{\pi }~\tilde{T}_{I}. \end{aligned}$$

(B11)

Thus the appearance of the peripheral domain where $\tilde{T}_{R}>\tilde{T}_{I}$ may indicate that the contribution of elastic scattering is going to be significant in the peripheral region, and even can be dominant if Eq. (B11) is satisfied. If such a situation occurs, the scattering becomes basically elastic.

Figure 10 shows various b-space differential cross sections using the amplitudes obtained in the present analysis. Note that the corresponding b-space amplitude satisfies the unitarity condition mentioned before, and

$$\begin{aligned} 0\le \mathrm{d}\sigma _\mathrm{el}/\mathrm{d}b, ~ ~ ~ \mathrm{d}\sigma _\mathrm{inel}/\mathrm{d}b \le 1. \end{aligned}$$

As seen from the figure, in all cases, although the real part amplitude becomes dominant over the imaginary part in the peripheral region, Eq. (B11) is far from being satisfied, and the inelastic contribution is totally dominant over the elastic contribution at these energies (7 and 8 TeV).