1 Introduction

The Einstein field equations admit simple and interesting solutions for hypothetical tunnels connecting two asymptotically flat universes, or two asymptotically flat portions of the same universe. A lot of attention has been paid to their geometrical properties and physical effects: apart from that wormholes would act as shortcuts connecting distant regions of spacetime, they can be used for constructing a time machine, for which a stable traversable wormhole is required [1,2,3,4,5].

The concept of a bridge connecting two spacetimes may be traced back to a work of Einstein and Rosen [6], who constructed an exact solution of the field equations corresponding to a spacetime of two identical sheets joined by a bridge. The Einstein–Rosen solution is the first ever example of wormholes, as we understand them today, and it can be related to the previous work of Flamm [7], who was the first to construct the isometric embedding of the Schwarzschild solution. The relation between Einstein–Rosen and Flamm solutions is discussed in Ref. [8].

Historically, the word wormhole was first coined by Misner and Wheeler [9]. Another term related to wormhole physics is the drainhole, which was formulated by Ellis [10]. In practice, the drainhole is a prototypical example of traversable wormholes, which is a spherically symmetric static solution of the usual coupled Einstein-scalar field equations, but with nonstandard coupling polarity [11].

In classical general relativity the matter content threading wormholes plays an important role. Typically, spherical traversable wormholes are discussed, and they may exist only in the presence of exotic matter, which may have even negative energy and would violate all energy conditions (EC) [1, 2, 12]. Today, the existence of such type of matter fields seems to be suitable due to the observed accelerated expansion of the universe, which can be explained by gravitational effects of the dark energy or phantom energy that also violates EC.

Static spherical wormholes supported by phantom energy also have been constructed [13, 14]. In this case the phantom matter threading the wormholes is an anisotropic fluid with a very strong negative radial pressure, satisfying the equation of state \(p_r/\rho <-1\), i.e. \(\rho +p_r<0\). The issue of matter supporting wormholes has been revisited in general relativity as well as in alternative theories, and it was shown that the requirement of exotic matter could in some cases be avoided. For example, cylindrically symmetric wormholes have deserved a considerable attention, mainly in relation to cosmic strings. Cylindrical wormhole throats may exist under slightly different conditions in comparison with spherically symmetric ones [15,16,17]. On the other hand, in Brans–Dicke gravity, Lorentzian wormholes are compatible with matter source which, apart from the Brans–Dicke scalar field, satisfies the EC [17, 18].

Asymptotically flat wormhole geometries are of particular interest [1, 2, 12], however, more general wormhole spacetimes also have been studied in the literature [19,20,21].

One interesting topic in wormhole physics is the study of thin-shell wormholes (with their stability properties). They are constructed by cutting and pasting two spherically symmetric manifolds to form a geodesically complete new one with a shell placed in the joining surface, i.e. the thin-shell is surrounding the wormhole [22]. Cylindrically symmetric thin-shell wormholes have also been explored [23, 24], as well as spherically symmetric thin-shell wormholes within the context of linear [25] and non-linear electrodynamics [26,27,28].

The Schwarzschild solution may be interpreted as an asymptotically flat wormhole, for which the shape function is given by \(b(r)=r_0=const\). However, this is a not traversable wormhole since this wormhole possesses a horizon at its throat. This is due to the redshift function has the form \(e^{2\phi (r)}=1-r_0/r\). One can construct Schwarzschild traversable wormhole versions by demanding that the redshift function does not have horizons and maintaining the radial metric component in the form \(-g_{rr}^{-1}=1-r_0/r\) [1, 2].

In this paper we consider a slight generalization of Schwarzschild traversable wormholes by considering the radial metric component given by \(-g_{rr}^{-1}=Const-r_0/r\), which implies that the shape function has the linear form \(b(r)=a_1r+r_0\), where \(a_1\) is a constant parameter. In such a way, we study static traversable wormholes with a linear shape function, which we call Schwarzschild-like wormholes.

The paper is organized as follows. In Sect. 2 we discuss the Morris–Thorne (M–T) wormhole formulation and obtain the field equations. In Sect. 3 we construct wormholes with a linear shape function. In Sect. 4 we examine in some detail zero-tidal-force Schwarzschild-like wormholes. In Sect. 5 we study the description of the geodesic behavior of zero-tidal-force Schwarzschild-like wormholes. In Sect. 6 we conclude with some remarks.

2 The Morris–Thorne wormhole formulation and field equations

Any static spherically symmetric wormhole is described by the metric

$$\begin{aligned} \mathrm{d}s^2=e^{2 \phi (r)} \mathrm{d}t^2- \frac{\mathrm{d}r^2}{1-\frac{b(r)}{r}}-r^2 \mathrm{d}\Omega ^2, \end{aligned}$$
(1)

where \(\mathrm{d}\Omega ^2= \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\varphi ^2\), \(e^{\phi (r)}\) and b(r) are the redshift and shape functions, respectively.

The redshift function must be non-zero and finite throughout the spacetime in order to ensure the absence of horizons and singularities. On the other hand, the shape function must satisfy the condition \(\frac{b(r)}{r} \le 1\), in order to the radial metric component \(g_{rr} < 0\). The equality sign holds only at the throat, where \(b(r_0) = r_0\), and \(r_0\) is the minimum value of r. Therefore, the wormhole shape function has a minimum at \(r = r_0\), where the wormhole throat is located. Thus, in Eq. (1), the radial coordinate covers the range \(r_0\le r< \infty \), while the angles are defined over the ranges \(0\le \theta \le \pi \) and \(0\le \varphi \le 2 \pi \), respectively.

Asymptotically flat wormhole geometries are of particular interest. In this sense, Morris and Thorne in their work [1, 2, 12] impose an additional restriction on the shape function \(\frac{b(r)}{r} \rightarrow 0\) as \(r \rightarrow \infty \). This constraint leads to a geometry connecting two asymptotically flat regions.

By assuming that the matter source threading the wormhole is described by the single anisotropic fluid \(T_\mu ^\nu =diag(\rho ,-p_r,-p_l,-p_l)\), from the Einstein field equations without a cosmological constant we obtain

$$\begin{aligned} \kappa \rho (r)= & {} \frac{b^{\prime }}{r^2}, \end{aligned}$$
(2)
$$\begin{aligned} \kappa p_r(r)= & {} 2\left( 1-\frac{b}{r} \right) \frac{\phi ^{\prime }}{r}-\frac{b}{r^3}, \end{aligned}$$
(3)
$$\begin{aligned} \kappa p_l(r)= & {} \left( 1-\frac{b}{r} \right) \nonumber \\&\times \left[ \phi ^{\prime \prime }+\phi ^{\prime \, 2} - \frac{b^\prime r+b-2r}{2r(r-b)} \, \phi ^\prime - \frac{b^\prime r-b}{2r^2(r-b)}\right] ,\nonumber \\ \end{aligned}$$
(4)

where a prime denotes \(\partial /\partial r\), \(\rho \) is the energy density, and \(p_r\) and \(p_l\) are the radial and lateral pressures, respectively.

To construct wormholes one may consider specific equations of state for \(p_r\) or \(p_l\), or restricted choices for the redshift and shape functions, among others. In this paper we shall use a specific form for the shape function.

3 Wormholes with linear shape functions

For constructing traversable wormholes the often used ansatz for the shape function is \(b(r)=r_0(r/r_0)^\alpha \), with \(0<\alpha <1\), for which is verified that if \(r \rightarrow \infty \) we have \(b(r)/r \rightarrow 0\). In this paper we shall consider a shape function with a linear dependence on the radial coordinate \(b(r)=\alpha + \beta r\), where \(\alpha \) and \(\beta \) are arbitrary constants. Evaluating at the throat, i.e. \(b(r_0) = \alpha + \beta r_0= r_0\), we find that \(\alpha = (1 - \beta )r_0\) and the shape function takes the form

$$\begin{aligned} b(r)=(1-\beta )r_0+\beta r, \end{aligned}$$
(5)

Notice that, from the proper radial distance \(l(r) = \pm \int ^r_{r_0} \frac{\mathrm{d}r}{\sqrt{1-\frac{b(r)}{r}}}\), it can be shown that at the throat always is satisfied the relation \(b^\prime (r_0) \le 1\) [12]. In particular, this implies that \(\beta \le 1\) for the shape function (5). On the other hand, if we apply the flare out condition [1, 2], expressed by \(\frac{\mathrm{d}^2r}{\mathrm{d}z^2}=\frac{b(r)-b(r)^\prime r}{2b(r)^2}>0\), we obtain that \(r_0(1-\beta )>0\). Therefore, for Schwarzschild wormholes (\(\beta =0\)) we have \(r_0>0\), while for Schwarzschild-like wormholes we have \(\beta <1\).

In conclusion, the wormhole metric is finally provided by

$$\begin{aligned} \mathrm{d}s^2=e^{2 \phi (r)} \mathrm{d}t^2- \frac{\mathrm{d}r^2}{\left( 1-\beta \right) \left( 1-\frac{r_0}{r}\right) }-r^2 \mathrm{d} \Omega ^2. \end{aligned}$$
(6)

From now on, we consider Schwarzschild-like wormholes defined by requiring that \(\beta <1\).

From Eq. (5) we see that at spatial infinity \(b(r)/r \rightarrow \beta \), so the condition \(\frac{b(r)}{r} \rightarrow 0\) is fulfilled only for a vanishing \(\beta \). Therefore, in general, Eq. (6) describes non-asymptotically flat wormholes, excluding the case \(\beta =0\), which with a non-zero and finite redshift function describes an asymptotically flat wormhole, as those considered by Morris and Thorne.

If \(e^{\phi (r)} \rightarrow const\) for \(r \rightarrow \infty \), then Eq. (6) becomes

$$\begin{aligned} \mathrm{d}s^2= \mathrm{d}t^2- \frac{\mathrm{d}r^2}{\left( 1-\beta \right) }-r^2 \mathrm{d} \Omega ^2, \end{aligned}$$
(7)

which describes a spacetime with a solid angle deficit (or excess). This can be seen directly by making the rescaling \(\varrho ^2=\frac{r^2}{1-\beta }\). Then the metric (7) becomes \(\mathrm{d}s^2= \mathrm{d}t^2- \mathrm{d}\varrho ^2-\left( 1-\beta \right) \varrho ^2 \mathrm{d} \Omega ^2\). This new form of the asymptotic metric (7) shows explicitly the presence of a solid angle deficit for \(0<\beta <1\), and a solid angle excess for \(\beta <0\), which vanish for \(\beta =0\), obtaining the standard Minkowski spacetime. It should be noted that the solid angle of a sphere of unity radius is now \(4\pi (1-\beta )<4 \pi \) for \(0<\beta <1\), and \(4\pi (1-\beta )>4 \pi \) for \(\beta <0\). For elucidating some features of this spacetime we can study associated embedding diagrams to it. One may visualize the shape and the size of slices \(t=const, \theta =\frac{\pi }{2}\) of the metrics (6) and (7) by using a standard embedding procedure in ordinary three-dimensional Euclidean space. In general, in order to embed two-dimensional slices \(t=const, \theta =\frac{\pi }{2}\) of the metric (1) we have to use the equation \(\frac{\mathrm{d}z(r)}{\mathrm{d}r}=\left( \frac{r}{b(r)}-1 \right) ^{-1/2}\) [1, 2]. This expression can be rewritten as \(\frac{\mathrm{d}z}{\mathrm{d}r}=\sqrt{\frac{b(r)}{r\left( 1-\frac{b(r)}{r}\right) }} \). Since \(r \ge r_0>0\) and \(1-b(r)/r>0\) the expression under the square root is positive if \(b(r)>0\), and negative if \(b(r)<0\), thus spacelike slices of any wormhole (1) can be embedded in a three-dimensional Euclidean space if \(b(r)>0\). In such a way, for the wormhole (6) the embedding takes the form \(\frac{\mathrm{d}z}{\mathrm{d}r}=\sqrt{\frac{(1-\beta )r_0+\beta r}{r\left( 1-\beta \right) \left( 1-\frac{r_0}{r}\right) }}\).

Fig. 1
figure 1

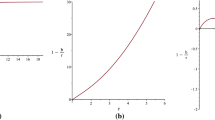
Plot a shows embedding diagrams of the metric (7) for slices \(t=const, \theta =\frac{\pi }{2}\) and \(\beta =\frac{1}{2},\frac{3}{4},\frac{9}{10}\) (solid, dashed and dotted lines, respectively). All slices exhibit a conical singularity due to the solid angle deficit of the metric (7). Plot b shows embeddings for Eqs. (6) and (7) (dashed and solid lines, respectively) with \(\beta =3/4\). For \(r \rightarrow \infty \) the distance between dashed and solid curves approaches zero. The dotted line represents the embedding of (6) with \(\beta =0\)

Full size image

Note that the numerator is everywhere positive for \(0\le \beta <1\). In this case \((1-\beta )r_0+\beta r \ge 1\), for \(r>r_0\), and the embedding extends from the throat to infinity. For \(\beta <0\) we have that \((1-\beta )r_0+\beta r >0\) for \(r_0 \le r < (1-1/\beta )r_0\), and \((1-\beta )r_0+\beta r \le 0\) for \(r \ge (1-1/\beta )r_0\), implying that the embedding exists only for \(r_0 \le r \le (1-1/\beta )r_0\). Thus, for slices \(t=const, \theta =\frac{\pi }{2}\) of (7) we obtain \(z_{c}(r)=\pm \frac{r}{\sqrt{\frac{1-\beta }{\beta }}}\). In Fig. 1a we show embedding diagrams for \(\beta =\frac{1}{2},\frac{3}{4},\frac{9}{10}\). In this case the spacetime has a solid angle deficit and its slices \(t=const, \theta =\frac{\pi }{2}\) exhibit a conical singularity. In Fig. 1b we show embeddings for Eq. (6) with \(\beta =0\), and Eqs. (6) and (7) with \(\beta =3/4\). It is interesting to note that for \(\beta =3/4\) and \(r \rightarrow \infty \) the distance between embeddings of Eqs. (6) and (7) approaches zero. Effectively, in this case the embedding function of metric (6) is given by \(\frac{\mathrm{d}z_1}{\mathrm{d}r}=\frac{\sqrt{3r+1}}{\sqrt{r-1}}\), which implies that

$$\begin{aligned} z_1(r)= & {} \sqrt{3r^2-2r-1} \\&+\frac{2}{\sqrt{3}} \ln \left( -\frac{1}{\sqrt{3}}+\sqrt{3}r+\sqrt{3r^2-2r-1} \right) . \end{aligned}$$

Note that \( \frac{\mathrm{d}z_1}{\mathrm{d}r} \rightarrow \sqrt{3}\) for \(r \rightarrow \infty \), therefore \(z_1(r)\) has an inclined asymptote with a slope of \(\sqrt{3}\). On the other hand, for the metric (7) we have \(\frac{\mathrm{d}z_2(r)}{\mathrm{d}r}=\sqrt{3}\), and therefore \(z_2(r)=\sqrt{3}r\). Clearly this implies that the inclined asymptote of \(z_1(r)\) is, at least, parallel to \(z_2(r)\), but we have \(\frac{z_1(r)}{z_2(r)} \rightarrow 1\) as \(r \rightarrow \infty \), which allows us to conclude that the distance between the embeddings discussed approaches zero.

For the metric (6) and \(r\ge r_0\), we have \(\kappa \rho =\beta /r^2\), which is positive for spacetimes with a solid angle deficit, and negative for spacetimes with a solid angle excess.

Fig. 2
figure 2

In plot a embeddings of (6), exhibiting a solid angle deficit, for slices \(t=const, \theta =\frac{\pi }{2}\) and \(\beta =0,\frac{1}{2},\frac{3}{4},\frac{9}{10}\) (solid, dashed, dotted and dash-dotted lines, respectively) are shown. For \(0\le \beta <1\) embeddings extend from \( r_0\) to infinity. In plot b embeddings of Eq. (6) and \(\beta =-\frac{1}{2},-1,-15\) (dashed, dotted and solid lines, respectively) are shown. The dash-dotted line corresponds to \(\beta =0\). For \(\beta <0\) embeddings extend from \(r_0\) to \(r_{\mathrm{max},i}=\frac{r_0(\beta -1)}{\beta }>r_0\), where \(i=1,2,3\)

Full size image

As we stated above, for \(0<\beta <1\) wormhole embeddings extend from the throat to infinity, and the constraint \(\frac{b(r)}{r} \rightarrow 0\) leads to a geometry connecting two asymptotically non-flat regions (strictly speaking asymptotically locally flat) of the form (7), but with a solid angle deficit. For slices of Eq. (6) we obtain \(z_{wh}(r)=\pm \frac{F + r_{0}\ln \left( \frac{r_{0}-2\beta r_{0} +2\beta r + F}{2\sqrt{\beta }} \right) }{2\sqrt{\left( 1-\beta \right) \beta }}\), where \(F=2\sqrt{\left( r- r_{0} \right) \left( \beta r -\beta r_{0} + r_{0} \right) }\). Notice that for \(r \rightarrow \infty \) we have \(z_{wh}(r) \approx \frac{r}{\sqrt{\frac{1-\beta }{\beta }}}+C=z_c(r)\), as we would expect (see Fig. 1b). In particular, for \(0<\beta <1\) the model describes a wormhole carrying a global monopole. In Fig. 2a we show embedding diagrams for \(\beta =0,\frac{1}{2},\frac{3}{4},\frac{9}{10}\).

If \(\beta <0\) the embeddings extend from the throat to a maximum value \(r_{\mathrm{max}}:=\frac{r_0(\beta -1)}{\beta }>r_0\). For \(\beta \rightarrow -0\) \(r_{\mathrm{max}} \rightarrow \infty \), while for \(\beta \rightarrow -\infty \) we have \(r_{\mathrm{max}} \rightarrow r_0\), allowing us to have wormhole embeddings of microscopic size. In Fig. 2b we show embeddings for (\(\beta =0,-\frac{1}{2},-1,-15\)), whose size depends on the amount of the angle excess. For \(r > r_{\mathrm{max}}\) wormhole slices cannot be embedded in an ordinary Euclidean space. Instead, a space with indefinite metric must be used. Nevertheless, one may match such a wormhole solution, as an interior spacetime, to an exterior vacuum spacetime at the finite junction surface \(r=r_{\mathrm{max}}\) (see Ref. [14]).

4 Zero-tidal-force Schwarzschild-like wormholes

A particularly simple wormhole class we shall examine in some detail is the set of zero-tidal-force Schwarzschild-like wormholes for which the metric has the form

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2- \frac{\mathrm{d}r^2}{\left( 1-\beta \right) \left( 1-\frac{r_0}{r}\right) }-r^2 \mathrm{d} \Omega ^2, \end{aligned}$$
(8)

and the energy density and pressures are given by

$$\begin{aligned} \kappa \rho =\frac{\beta }{r^2}, \kappa p_r=\frac{r_0(\beta -1)}{r^3}-\frac{\beta }{r^2}, \kappa p_l =-\frac{r_0(\beta -1)}{2 r^3}.\nonumber \\ \end{aligned}$$
(9)

Note that at the throat \(p_r(r_0)=-1/r_0^2<0\), while \(p_l(r_0)=-(\beta -1)/(2r_0^2)\), and it is positive for \(\beta <1\). The radial pressure vanishes at the defined above surface \(r_{\mathrm{max}}:=r_0(\beta -1)/\beta \). For \(0<\beta <1\), \(r_{\mathrm{max}}<0\), and, for \(\beta <0\), \(r_{\mathrm{max}}>0\). This implies that for \(r\ge r_0\) the radial pressure is negative if \(0<\beta <1\), while for \(\beta <0\) we obtain that \(p_r<0\) for \(r_0 \le r<r_{\mathrm{max}}\), and \(p_r>0\) if \(r>r_{\mathrm{max}}\). The lateral pressure is positive for any \(\beta <1\). For the null EC (NEC), i.e. \(\rho +p_i \ge 0\), we obtain \(\rho +p_r=r_0(\beta -1)/r^3\), thus \(p_r\) does not fulfill NEC. On the other hand, \(\rho +p_l=\beta /r^2-\frac{r_0(\beta -1)}{2 r^3}\), so \(p_l\) fulfills NEC for \(r \ge r_0\) if \(0<\beta <1\), and for \(r_0<r<r_{\mathrm{max}}/2\) if \(-1<\beta <0\); lastly if \(\beta <-1\) we have \(\rho +p_l<0\) for \(r \ge r_0\). It is remarkable that \(\rho +p_{\mathrm{total}}=\rho +p_r+2p_l= 0\). Hence the null (\(\rho +p_i \ge 0\)), weak (\(\rho \ge 0\) and \(\rho +p_i \ge 0\)), strong (\(\rho +p_i \ge 0\) and \(\rho +p_{\mathrm{total}} \ge 0\)) and dominant (\(\rho \ge 0\) and \(p_i \le |\rho |\)) EC are not fulfilled for \(r \ge r_0\).

Due to \(\rho >0\), \(p_r<0\) and \(p_l>0\), for \(r\ge r_0\) and \(0<\beta <1\), Eq. (8) describes a phantom wormhole carrying a global monopole: the right-hand side of Eq. (9) represents the components of the energy-momentum tensor, which includes the effects produced in the geometry by two distinct objects: the global monopole (for which \(r_0=0\) and \(\rho =-p_r=\beta /(\kappa r^2)\), \(p_l=0\)), and the wormhole itself (for which \(\beta =0\) and \(\rho =0\), \(p_r=-2p_l=-r_0/r^3\)). Global monopoles are known for producing a solid angle deficit at infinity [29,30,31]. By tuning the parameter \(\beta \), one can make the solid angle deficit arbitrarily close to \(4 \pi \). Notice that the wormhole \(\beta =0\) is a particular solution of the selfdual Lorentzian wormhole with a vanishing energy density as discussed in Ref. [32, 33].

Let us now focus to traversability conditions of the zero-tidal-force Schwarzschild-like wormhole (8). We shall suppose that a traveler journeys radially through the wormhole (8), beginning at rest in the space station 1 in the lower universe, and ending at rest in a space station 2 in the upper universe.

An important traversability condition required is that the acceleration felt by the traveler should not exceed Earth gravity \(g_{_\oplus }=980 \, \mathrm{cm/s}^2\). As shown in Ref. [1, 2], the acceleration felt by the radially moving traveler is given by

$$\begin{aligned} a=\pm \left( 1-\frac{b(r)}{r} \right) ^\frac{1}{2} e^{-\phi (r)} (\gamma e^{\phi (r)})^\prime c^2, \end{aligned}$$

where \(e^\phi (r)\) and b(r) are the redshift and shape functions of the metric (1); and \(\gamma =\left( 1-\frac{v(r)^2}{c^2} \right) ^{-1}\), v(r) being the radial velocity of the traveler as she passes radius r, as measured by a static observer at r. Then for the zero-tidal-force wormhole (8) we see that the constraint is given by

$$\begin{aligned} |a|=\left| \left( (1-\beta )\left( 1-\frac{r_0}{r} \right) \right) ^\frac{1}{2} \gamma ^\prime c^2 \right| \lesssim g_{_\oplus }. \end{aligned}$$

For a Schwarzschild wormhole the acceleration felt by a traveler is given by \(|a_{Sch}|=\left| \left( 1-\frac{r_0}{r} \right) ^\frac{1}{2} \gamma ^\prime c^2 \right| \). Therefore, for a given radius r between stations 1 and 2, the acceleration is lower than \(|a_{Sch}|\) for Schwarzschild-like wormholes exhibiting a solid angle deficit due to \(0<\beta <1\), while it is greater than \(|a_{Sch}|\) for wormholes exhibiting a solid angle excess, since \(\beta <0\). This constraint may be trivially satisfied, independently of the value of \(\beta \), by requiring that the traveler maintains constant speed v throughout her trip from the station 1 to the station 2 (by ignoring the acceleration at leaving station 1 and the deceleration upon arriving at station 2).

Another important traversability condition is related to the tidal accelerations felt by the traveler (for example between head and feet), which should not exceed the Earth’s gravitational acceleration. As shown in Ref. [1, 2] the radial and lateral tidal constraints are given by

$$\begin{aligned}&\left| \left( 1-\frac{b}{r} \right) \left( -\phi ^{\prime \prime } - \phi ^{\prime 2}+\frac{b^\prime r-b}{2r (r-b) } \phi ^\prime \right) c^2 \right| \left| \xi \right| \lesssim g_{_\oplus }, \\&\quad \left| \frac{\gamma ^2 c^2}{2r^2} \left[ \left( \frac{v}{c} \right) ^2 \left( b^\prime -\frac{b}{r} \right) +2( r-b )\phi ^\prime \right] \right| \left| \xi \right| \lesssim g_{_\oplus }, \end{aligned}$$

respectively, where \(\xi \) represents the size of the traveler’s body. The radial tidal constraint can be regarded as constraining the redshift function, while the lateral tidal constraint can be regarded as constraining the speed v with which the traveler crosses the wormhole [1, 2].

In the case of zero-tidal-force Schwarzschild-like wormhole (8) we conclude that the radial tidal constraint is everywhere identically zero. On the other hand, for the lateral tidal constraint we obtain \(\left| \frac{\gamma ^2 v^2}{2r^3} \, r_0 \left( \beta -1 \right) \right| \left| \xi \right| \lesssim g_{_\oplus }\). In the limit that the motion is nonrelativistic we have \(v<<c\) and then \(\gamma \approx 1\). Therefore we have

$$\begin{aligned} \left| \frac{v^2}{2r^3} \, r_0 \left( \beta -1 \right) \right| \left| \xi \right| \lesssim g_{_\oplus }. \end{aligned}$$

This constraint is more severe at the smallest radial value, i.e. at the throat. So evaluating at \(r_0\), and by considering that the size of the traveler’s body is 2 m, we obtain for the traveler’s speed

$$\begin{aligned} v \lesssim \frac{3 \sqrt{2} }{\sqrt{\left| \beta -1 \right| }} \, r_0. \end{aligned}$$
(10)

Now some words about the total travel time from station 1 to station 2. Standard M–T wormhole spacetimes are flat at spatial infinity; for this reason, in order for the stations to be located not at spatial infinity, but near the wormhole, Morris and Thorne put stations 1 and 2 in regions that are very nearly flat. In such a way, in the standard M–T procedure the stations are located at radii where the factor \(1-b(r)/r\) differs from unity by only \(1\%\) [1, 2].

If we apply the same criterion we must require the condition \((1-\beta )(1-r_0/r) =0.99\), which gives the relation for the radial location of stations

$$\begin{aligned} r_1=r_2=\frac{100 (1-\beta )}{1-100 \beta } \, r_0. \end{aligned}$$
(11)

For the asymptotically flat Schwarzschild wormhole (\(\beta =0\)) this means that stations are located at \(r_1=r_2=10^2 r_0\). For zero-tidal-force Schwarzschild-like wormholes with \(\beta <0\) we have that \(r_{1,2} \rightarrow 10^2 r_0\) if \(\beta \rightarrow -0\), while \(r_{1,2} \rightarrow r_0\) if \(\beta \rightarrow -\infty \). Therefore, for spacetimes with solid angle excess the stations may be located at \(r_0<r_{1,2}< 10^2 r_0\).

For calculating the total travel time we need to know the total proper distance between stations 1 and 2, which is defined by \(l(r)=\pm \int _{r_0}^r \frac{\mathrm{d}r}{\sqrt{1-b/r}}\). For the Schwarzschild-like wormhole (8) we obtain

$$\begin{aligned} l(r)=\pm \frac{2\sqrt{r(r-r_0)}+r_0 \ln \left( \frac{-r_0+2r+2\sqrt{r(r-r_0)}}{r_0} \right) }{2 \sqrt{1-\beta }}. \end{aligned}$$

Evaluating this function at \(r_1\) and \(r_2\) we obtain

$$\begin{aligned} l(r_1)= & {} \frac{2r_0\sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } +r_0 \ln \left( \frac{199-100 \beta }{1-100 \beta }+2 \sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } \right) }{2 \sqrt{1-\beta }}, \\ l(r_2)= & {} -\frac{2r_0\sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } +r_0 \ln \left( \frac{199-100 \beta }{1-100 \beta }+2 \sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } \right) }{2 \sqrt{1-\beta }}, \end{aligned}$$

and therefore the total proper distance between stations is

$$\begin{aligned} \bigtriangleup l=\frac{2r_0\sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } +r_0 \ln \left( \frac{199-100 \beta }{1-100 \beta }+2 \sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } \right) }{ \sqrt{1-\beta }}. \end{aligned}$$

Now, if the traveler journeys with constant speed (10), then the total time travel is given by

$$\begin{aligned} \bigtriangleup t= & {} \frac{\bigtriangleup l}{v} \\= & {} \frac{ \left( 2\sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } +\ln \left( \frac{199-100 \beta }{1-100 \beta }+2 \sqrt{\frac{9900(1-\beta )}{(1-100 \beta )^2} } \right) \right) }{ 3\sqrt{2}}. \end{aligned}$$

From this expression we have for the total travel time that if \(-\infty< \beta <0\) then \(0 \,\mathrm{s}<\bigtriangleup t<24.158\) s. Since for \(\beta =0\) the total travel time is 24.158 s, we conclude that the presence of a solid angle excess allows the traveler to make the trip in a shorter time lapse.

For wormholes with \(0<\beta <1\) we have from Eq. (11) that \(r_1\) and \(r_2\) are positive only if \(0<\beta <1/100\). Therefore, for zero-tidal-force Schwarzschild-like wormholes with solid angle deficit, it is possible to locate stations where the curvature of the wormhole is negligible (with deviations of \(1 \%\) from flatness) only if \(\beta \approx 0\). Note that for \(0<\beta <1/100\) we have \(100 r_0<r_{1,2}<\infty \). If we compare this case with asymptotically flat wormholes, we see that the solid angle deficit imposes the requirement that stations be located further away from the throat, contrary to what happens with wormholes with solid angle excess. In this case we have for the total travel time: \(24.158 \,s<\bigtriangleup t< \infty \), thus in the presence of a solid angle deficit the traveler makes the trip in a longer time lapse than for \(\beta \le 0\).

Lastly, we should note that the total time lapse \(\bigtriangleup t\) for travel from station 1 to station 2 is the same for the traveler as well as for observers at both stations.

5 Geodesics

Now we shall consider a description of the geodesic behavior for zero-tidal-force Schwarzschild-like wormholes (8), corresponding to different values of \(\beta \). To proceed we use the Lagrangian \(\mathcal {L}=\frac{1}{2} g_{\alpha \beta } \frac{\mathrm{d}x^\alpha }{\mathrm{d} \tau }\frac{\mathrm{d}x^\beta }{\mathrm{d} \tau }\) associated to the metric (8),

$$\begin{aligned} \mathcal {L} =\frac{1}{2} \left[ \dot{t}^2-\frac{\dot{r}^2}{(1-\beta )(1-\frac{r_0}{r})}-r^2 \dot{\theta }^2-r^2 \sin ^2 \theta \dot{\varphi }^2 \right] ,\nonumber \\ \end{aligned}$$
(12)

and the conserved conjugate momenta \(\Pi _t\) and \(\Pi _\varphi \) are

$$\begin{aligned} \Pi _t=\frac{\partial \mathcal {L}}{\partial \dot{t}}= \dot{t}=E, \Pi _\varphi =-\frac{\partial \mathcal {L}}{\partial \dot{\varphi }}=r^2 \sin ^2 \theta \dot{\varphi }=const.\nonumber \\ \end{aligned}$$
(13)

Because we deal with spherical metric (8) we shall consider the test particle paths confined to the plane \(\theta =\pi /2\). Therefore we have

$$\begin{aligned} E^2=h+\frac{L^2}{r^2} +\frac{\dot{r}^2}{(1-\beta )(1-\frac{r_0}{r})}, \,\,\,\,\, r^2 \dot{\varphi }=L, \end{aligned}$$
(14)

where \(h=1\) for time-like geodesics and \(h=0\) for null geodesics and L is the angular momentum per unit mass.

Let us now explore radial time-like geodesics. To do this we must put \(L=0\) and \(h=1\) and consider initial conditions for Eq. (14). Specifically, the initial position \((t_i,r_i)\) and the initial velocity \(v_i\). We shall suppose that the test particle, at \(t_i=0\), starts to move at \(r_i\) with initial velocity \(v_i\). These initial conditions imply that

$$\begin{aligned} E^2=1+\frac{1}{(1-\beta )(1-\frac{r_0}{r_i})} \, v_i^2, \end{aligned}$$
(15)

and Eq. (14) may be written as

$$\begin{aligned} \pm \sqrt{\frac{1-\frac{r_0}{r}}{1-\frac{r_0}{r_i}} \, v_i^2}=\dot{r}, \end{aligned}$$
(16)

where the − sign is valid for particles moving from \(r_i\) towards the wormhole throat, while the \(+\) sign for particles moving from \(r_i\) to infinity. We note that in the former case the particle starts to move with the velocity \(v_i>0\) and tends to the maximum value \(v_{\mathrm{max}}=v_i/\sqrt{1-r_0/r_i}\).

It becomes clear that if the test particle has zero initial velocity, i.e. \(v_i=0\), then \(\dot{r}=0\) and \(r(\tau )=const\), implying that the test particle will remain at rest at the initial position \(r_i\). This means that we need to give the particle an initial velocity \(v_i \ne 0\) in order to push it towards the throat or ti infinity. However, notice that Eq. (16) implies that time-like geodesics starting at \(r_i>r_0\) with initial velocity \(v_i\) will always reach the throat with zero velocity, due to the requirement \(r=r_0\) at the throat.

From Eq. (15) we may write \(v_i^2=(E^2-1)(1-\beta )(1-r_0/r_i)\), and since the \(\beta \)-parameter is restricted to the range \(\beta <1\) and \(r_i \ge r_0\), then we conclude that \(E^2 \ge 1\). The value \(E^2=1\) implies that the particle is at rest.

By deriving Eq. (16) with respect to the affine parameter \(\tau \) we obtain for the second derivative of the radial coordinate \(\ddot{r}=\frac{(E^2-1)(1-\beta )r_0}{2r^2}\), which is everywhere positive. The presence of a solid angle deficit or excess does not play any role in the sign of the acceleration since to \(\beta <1\). To this second derivative there may be associated a pseudo Newton law \(\ddot{r}=-V_{\mathrm{eff}}^{\prime }/2\) [34], where \(V_{\mathrm{eff}}\) is an effective potential and \(\prime =\partial /\partial r\). Then the acceleration \(\ddot{r}=\frac{(E^2-1)(1-\beta )r_0}{2r^2}\) shows us that the gravitational field is everywhere repulsive. This is valid only for radially moving test particles, since for objects at rest we have \(E^2=1\) (see Eq. (15)), and then the expression for \(\ddot{r}\) implies that they possess a zero radial acceleration.

In order to see the qualitative behavior of time-like radial geodesics starting to move at \(r_i\) with initial velocity \(v_i\) we solve Eq. (16), whose solution is given by

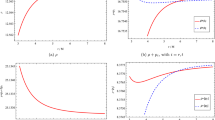
$$\begin{aligned} \tau (r)= & {} \pm \frac{\sqrt{1-\frac{r_0}{r_i}}}{2 v_i} \nonumber \\&\times \left( 2\sqrt{r^2-r_0r}+r_0 \ln \left( -\frac{r_0}{2}+r+\sqrt{r^2-r_0r} \right) \right) +C,\nonumber \\ \end{aligned}$$
(17)

where C is an integration constant. We want to describe a particle starting to move from \(r_i\) at \(\tau =0\), so we shall impose the initial condition \(\tau (r_i)=0\). In Fig. 3a we plot both solution branches (17) as \(r=r(\tau )\). The test particle which moves towards the throat, reaches it at a finite time (with a zero velocity). On the other hand, the radial outwards geodesic reaches infinity. This result is in agreement with the fact that in this case the effective potential has a repulsive character. In Fig. 3b we show the velocity as a function of the radial coordinate corresponding to radial outwards geodesic (the upper curve) and the radial inwards geodesic (the lower curve). For the radial inwards geodesic (\(v_i =- 3\)) the particle reaches the throat with zero velocity, while for the radial outwards geodesic (\(v_i =3\)) the particle velocity tends to the maximum value \(v_{\mathrm{max}}=3\sqrt{2}\).

Fig. 3
figure 3

The profile of radial outwards (\(+\) sign) and radial inwards (− sign) geodesics of Eq. (17) are plotted in a. Both start from \(r_i=4\) with initial velocity \(v_i \ne 0\) at \(\tau =0\) (\(r_0=2\)). The radial outwards geodesic (the upper curve) reaches infinity, while the inwards one reaches \(r_0\) at a finite time, ending up with a zero velocity, since \(\frac{\mathrm{d}r}{\mathrm{d}\tau }|_{r_0}=0\) (the lower curve). In b radial outwards (the upper curve) and radial inwards (the lower curve) geodesics of Fig. 3a are plotted. Both particles start to move at \(r_i=4\) with initial velocity \(v_i =\pm 3\) (\(r_0=2\)). For the radial inwards geodesic (\(v_i =- 3\)) the particle reaches the throat with zero velocity, while for the radial outwards geodesic (\(v_i =3\)) we have \(v \rightarrow v_{\mathrm{max}}=3\sqrt{2}\)

Full size image

Let us now explore non-radial time-like geodesics, i.e. paths satisfying \(L \ne 0\) and \(h=1\). In this case the relevant equations of motion are Eq. (14), therefore the initial condition to be considered are position \((r_i,\varphi _i)\) and the initial radial velocity \(\dot{r}_i\) and angular velocity \(\dot{\varphi }_i\). We shall suppose that the test particle starts to move at \(r_i\) with initial radial and angular velocities \(v_i\) and \(\dot{\varphi }_i\), respectively.

For Eq. (14) the initial conditions imply that for a test particle starting to move at \(r_i\) with initial radial velocity \(v_i\) we have

$$\begin{aligned} E^2=1+\frac{L^2}{r_i^2} +\frac{v_i^2}{(1-\beta )(1-\frac{r_0}{r_i})}, \end{aligned}$$
(18)

and then Eq. (14) becomes

$$\begin{aligned}&\left( L^2 \left( \frac{1}{r_i^2}-\frac{1}{r^2} \right) +\frac{v_i^2}{(1-\beta )(1-\frac{r_0}{r_i})} \right) \nonumber \\&\quad \times \left( 1-\frac{r_0}{r} \right) \left( 1-\beta \right) =\dot{r}^2. \end{aligned}$$
(19)

This equation reduces to Eq. (16) if \(L=0\). On the other hand, for \(r^2 \dot{\varphi }=L\) the initial conditions imply that for a particle starting to move at \(r_i\) with initial angular velocity \(\dot{\varphi }_i\) we have \(r_i^2 \dot{\varphi }_i=L\). We shall see later that the presence of the angular momentum L in Eq. (19) allows the \(\beta \)-parameter influences the trajectories of non-circular geodesics of the spacetime (8). For circular geodesics it must be required that its radial velocity vanishes, i.e. \(\mathrm{d}r/\mathrm{d}\tau =0\). From Eq. (19) we see that the acceleration for \(\dot{r}=0\) is given by

$$\begin{aligned} \ddot{r}=(1-\beta )\left( 1-\frac{r_0}{r}\right) \frac{L^2}{r^3}, \end{aligned}$$
(20)

implying that \(\ddot{r} \ge 0\) everywhere. Since \(\ddot{r}\) vanishes only at \(r=r_0\), then circular orbits only exist at the wormhole throat. For any other location \(r>r_0\) if the test particle has zero radial velocity it will be always accelerated in the direction of increasing r.

Now, let us note that Eq. (19) implies that the test particle has zero radial velocity at \(r_0\) and at the radius

$$\begin{aligned} r_{\mathrm{zero}}=\left( \frac{1}{r_i^2}+\frac{v_i^2}{L^2(1-\beta ) \left( 1-\frac{r_0}{r_i}\right) } \right) ^{-1/2}>0. \end{aligned}$$
(21)

If the condition \(r_{\mathrm{zero}}>r_0\) is satisfied, the radius (21) represents for a geodesic starting at \(r_i>r_0\) with \(v_i<0\) and \(\dot{\varphi }_i \ne 0\) a point of reversal, since at this radius (\(r_{\mathrm{zero}}<r_i\)) the test particle, which approaches to the throat, is deflected by the wormhole. In other words, \(r_{\mathrm{zero}}\) represents the minimum distance to the wormhole throat which can be reached by a test particle. In this case the time-like geodesic lies always on the one side of the wormhole (or on the other) and the test particle does not cross the throat (see Figs. 4a, 5).

Fig. 4
figure 4

The behavior of the radial velocity for the geodesics \(G_1\) (dotted line) and \(G_2\) (solid line) with a same value of L is shown in a. The throat is located at \(r_0=1\). The velocities for a given common value \(r_i>r_0\) satisfy the condition \(|v_{_{G1}}(r_i)|>|v_{_{G2}}(r_i)|\). We see that both geodesics are confined to one side of the wormhole. The reversal radius are different: for \(G_1\) the turning point is located at the wormhole throat, while for \(G_2\) the turning point is located at a radius greater than \(r_0\). In b, the qualitative behavior for the branch \(\dot{l}=\sqrt{E^2-1-\frac{L^2}{r(l)^2}}\) is shown for different values of E, L and \(r_0\). For dashed curves \(\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}} \ge 0\), then reversal points do exist, while for the solid curve \(\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}} <0\), so geodesics reach the throat, where the minimum speed is reached, and they pass to the other wormhole side

Full size image
Fig. 5
figure 5

Plots a–c show embedding diagrams for the case where non-radial geodesics are confined to one side of the wormhole, and \(r_0=1\), \(\beta =-1/2, 0, 1/2\). In this case geodesics do not cross the throat since they satisfy the condition \(\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}} \ge 0\), and therefore there exist reversal points. In c we show geodesics which overlap with itself in one caustic point. Plots d–f show embedding diagrams for passing non-radial geodesics through the wormhole throat, which satisfy the condition \(\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}} < 0\)

Full size image

For a test particle starting to move at some \(r_{i0}>r_0\) with zero velocity, Eqs. (20) and (21) imply that the particle will start to move from this location \(r_{i0}\) to the spatial infinity, following a specific geodesic path that would have initially had some velocity \(v_i<0\) at some \(r_i>r_{i0}\), which further satisfies the condition \(r_{\mathrm{zero}}=r_{i0}\). Additionally, it should be considered that Eq. (19) implies that outward geodesics have a limit for the radial velocity given by \(v_{_{limit}}= [L^2(1-\beta )/r_i^2+v_i^2/(1-r_0/r_i)]^{1/2}\).

It can be shown also that there exist inward time-like geodesics that cross the throat. In order to show this we shall rewrite Eq. (14) by introducing the rescaling \(\mathrm{d}l=\pm \frac{\mathrm{d}r}{\sqrt{(1-\beta )(1-\frac{r_0}{r})}}\), which implies that

$$\begin{aligned} l(r)=\pm \frac{2\sqrt{r(r-r_0)}+r_0\ln \left( \frac{-\frac{1}{2}r_0+r+\sqrt{r(r-r_0)}}{\frac{r_0}{2}}\right) }{2\sqrt{1-\beta }}, \end{aligned}$$
(22)

where we have used the integration constant for imposing the requirement that the throat be located at \(l=0\), i.e. \(l(r_0)=0\). Additionally, Eq. (22) implies that for \(r_0\le r <\infty \) the introduced l-coordinate satisfies \(-\infty<l< \infty \).

In such a way, Eq. (14) takes the form \(\dot{l}^2=E^2-1-\frac{L^2}{r(l)^2}\), where \(\dot{l}=\frac{\mathrm{d}l}{\mathrm{d}\tau }\) and r(l) is the inverse function of Eq. (22). In order to have \(\dot{l}^2 > 0\) we must impose on the energy the condition \(E^2>1\). It should be noted that in this case the metric (8) is provided by \(\mathrm{d}s^2=\mathrm{d}t^2-\mathrm{d}l^2-r(l)^2 \mathrm{d} \Omega ^2\), where l is the proper radial coordinate. For finding the turning points discussed above we must require \(\dot{l}=0\) in \(\dot{l}^2=E^2-1-\frac{L^2}{r(l)^2}\). This condition is satisfied for \(r_{\mathrm{zero}}(l)= \frac{L}{\sqrt{E^2-1}} \ge r_0\), and by using Eq. (18) this equation takes the form (21). We can find the values of \(l_{\mathrm{zero}}\) by putting \(r_{\mathrm{zero}}(l)\) into Eq. (22), which allows us to find

$$\begin{aligned} l_{\mathrm{zero}}= & {} \pm \frac{1}{2\sqrt{1-\beta }} \left[ 2\sqrt{\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}}}\right. \nonumber \\&\left. +r_0 \ln \left( -1 + \frac{2L}{r_0\sqrt{E^2-1}}+\frac{2}{r_0}\sqrt{\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}}} \right) \right] .\nonumber \\ \end{aligned}$$
(23)

Reversal points do exist only for \(\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}} \ge 0\) and \( \frac{2L}{r_0\sqrt{E^2-1}}+\frac{2}{r_0}\sqrt{\frac{L^2}{E^2-1} - \frac{r_0 L}{\sqrt{E^2-1}}} >1\). If the parameters E, L and \(r_0\) do not satisfy these constraints then reversal points do not exist and the geodesics pass to the other wormhole side (this is shown in Fig. 4b).

6 Conclusions

We have presented new static traversable wormholes, dubbed Schwarzschild-like wormholes, by considering a specific shape function with a linear dependence on the radial coordinate. The solution is given by Eq. (6) and represents a geometry connecting two asymptotically non-flat regions due to the presence of a solid angle deficit or a solid angle excess, which is characterized by the constant \(\beta \) (\(0<\beta <1\) for angle deficit, and \(\beta <0\) for angle excess). In the first case, the embeddings extend from the throat to infinity (see for example Fig. 2a). In the second case, the embeddings extend from the throat to maximum radial value (see Fig. 2b). Therefore, the shape and the size of the wormhole embeddings depend on the amount of the solid angle deficit or excess.

We examined in some detail the set of zero-tidal-force Schwarzschild-like wormholes. In the framework of these solutions we discuss a phantom wormhole carrying a global monopole. In the case of solid angle deficit, the energy-momentum tensor includes two distinct objects, namely a global monopole and the wormhole itself. These wormholes are sustained by anisotropic matter source in which the null, weak, strong and dominant EC are not fulfilled for \(r\ge r_0\).

We have also considered a description of the geodesic behavior for zero-tidal-force Schwarzschild-like wormholes (8), corresponding to different values of the \(\beta \)-parameter. The analysis of the Euler–Lagrange equation shows that a test particle, radially moving toward the throat, always reaches it with a zero velocity at a finite time, while for radial outwards geodesics the particle velocity tends to of maximum value, reaching the infinity. On the other hand, for non-radial geodesics we derive the conditions which must be fulfilled in order to geodesics cross the throat. In such a way, we show that if reversal points do exist the geodesics are confined to one side of the wormhole, while if reversal points do not exist, the geodesics cross the throat (see Fig. 5). For plotting Fig. 5, besides equation \(r^2 \dot{\varphi }=L\), we have used the radial Euler–Lagrange equation \(-\frac{\ddot{r}}{(1-\beta )(1-\frac{r_0}{r})} + \frac{r_0 \left( E^2 -h-\frac{L^2}{r^2} \right) }{2 (1-\frac{r_0}{r}) r^2 }+\frac{L^2}{r^3}=0\), which we solved numerically.