1 Introduction

The properties of the quantum vacuum are sensitive to both the local and the global geometrical characteristics of the background spacetime. In this paper we investigate the electromagnetic vacuum polarization sourced by the gravitational field and by the nontrivial topology due to the presence of a straight cosmic string. In order to have an exactly solvable problem, as the background geometry we will consider a spacetime that is maximally symmetric in the absence of the cosmic string, namely de Sitter (dS) spacetime. For the cosmic string a simplified model will be taken in which the local geometry outside the core is not changed by the presence of the string: the only effect is the planar angle deficit depending on the mass density of the string.

In addition to the high degree of symmetry, our choice of dS spacetime as the background geometry is motivated by its importance in modern cosmology. In most inflationary models the early expansion of the universe is approximated by the dS phase (for reviews see [1,2,3,4]). The presence of this phase before the radiation dominated era naturally solves several problems in the standard cosmological model. More recently, the astronomical observations of high redshift supernovae, galaxy clusters, and cosmic microwave background [5,6,7,8,9,10,11] indicate that at the present epoch the universe is accelerating and the corresponding expansion is dominated by a source of the cosmological constant type. In this case, the dS spacetime appears as the future attractor for the geometry of the universe. Consequently, the investigation of physical effects in dS spacetime is important for understanding both the early universe and its future evolution. A topic which has received increasing attention is related to string-theoretical models of dS spacetime and inflation. Recently several constructions of metastable dS vacua within the framework of string theory are discussed (see, for instance, reviews [12, 13]).

The investigation of the quantum field theoretical effects in dS spacetime is of considerable interest. These effects may have important implications in cosmology. During an inflationary epoch, quantum fluctuations in the inflaton field introduce inhomogeneities which play a central role in the generation of cosmic structures from inflation. The inflation also provides an attractive mechanism of producing long-wavelength electromagnetic fluctuations, originating from subhorizon-sized quantum fluctuations of the electromagnetic field stretched by the dS phase to superhorizon scales. After these long-wavelength fluctuations have re-entered the horizon in the post-inflationary era, they can serve as seeds for cosmological magnetic fields. Related to this inflationary mechanism for the generation of the seeds, the cosmological dynamics of the electromagnetic field quantum fluctuations have been discussed in a large number of papers (for reviews see [14,15,16,17]).

In the present paper we investigate the influence of a cosmic string on the vacuum fluctuations of the electromagnetic field in background of dS spacetime (for the effects of inflation on the cosmic strings see, for instance, [18,19,20,21]). Though the cosmic strings produced in phase transitions before or during early stages of inflation are diluted by the expansion to at most one per Hubble radius, the formation of defects near or at the end of inflation can be triggered by several mechanisms (see [22, 23] for possible distinctive signals from such models). They include a coupling of the symmetry breaking field to the inflaton field or to the curvature of the background spacetime. Moreover, one can have various inflationary stages, with linear defects being formed in between them [24]. Depending on the underlying microscopic model, there exist several kinds of cosmic strings. They can be either nontrivial field configurations or more fundamental objects in superstring theories. The cosmic strings are among the most popular topological defects formed by the symmetry breaking phase transitions in the early universe within the framework of the Kibble mechanism [25]. They are sources of a number of interesting physical effects that include the generation of gravitational waves, high-energy cosmic rays, and gamma ray bursts. Among the other signatures are the gravitational lensing and the creation of small non-Gaussianities in the cosmic microwave background. The cosmic superstrings, which are fundamental quantum strings stretched to cosmological scales, were first considered in [26]. More recently, a mechanism for the generation of this type of objects with low values of the string tensions is proposed within the framework of brane inflationary models [13, 22, 23, 27]. In these models the accelerated expansion of the universe is a consequence of the motion of branes in warped and compact extra dimensions.

Although the specific properties of cosmic strings are model-dependent, they produce similar gravitational effects. In the simplified model with the string-induced planar angle deficit, the nontrivial spatial topology results in the distortion of the vacuum fluctuations spectrum of quantized fields and induces shifts in vacuum expectation values (VEVs) of physical characteristics of the vacuum state such as the field squared and the energy-momentum tensor. Explicit calculations of this effect have been done for scalar, fermion and vector fields (see references given in [28, 29]). For charged fields, another important characteristic of the vacuum state is the VEV of the current density (see [30, 31] for a recent discussion and references therein). The analysis of the vacuum polarization effects induced by a cosmic string in dS spacetime for massive scalar and fermionic fields has been presented in [32,33,34]. Here we will be concerned with the combined effects of the background gravitational field and of a cosmic string on the correlators for the electric and magnetic fields and on the VEVs of the energy density and squared electric and magnetic fields. The problem will be considered on the bulk of dS spacetime with an arbitrary number of spatial dimensions D. This is motivated by several reasons. In discussions of cosmic superstrings, depending on the compactification scheme of extra dimensions, one can have \(3\leqslant D\leqslant 9\). In particular, this is the case for superstrings formed at the end of brane inflation. The consideration of electrodynamics in spatial dimensions \(D>3\) is a natural way to break the conformal invariance of the \(D=3\) theory. The breaking of conformal invariance is required in inflationary models for the generation of large-scale magnetic fields. Usually this is done by adding additional couplings of the electromagnetic field (for example, to the inflaton field) [14,15,16,17]. A mechanism for the generation of cosmological magnetic fields, based on the dynamics of electromagnetic fluctuations in models with \(D>3\), has been discussed in [35]. The consideration of quantum field theories in a number of spatial dimensions other than 3 is also required in dimensional regularization procedure for the ultraviolet divergences.

The paper is organized as follows. In the next section the background geometry is described and a complete set of mode functions for the electromagnetic field is given. In Sect. 3, two-point functions for the vector potential and for the electric field strength are investigated. The VEV of the electric field squared is discussed in Sect. 4. The part induced by the nontrivial topology of the cosmic string is explicitly separated and its asymptotic behavior in various limiting regions is investigated. The two-point functions corresponding to the Lagrangian density and the magnetic field are considered in Sect. 5. The topological contributions in the VEVs of the squared magnetic field and of the vacuum energy density are investigated. The main results are summarized in Sect. 6. In the appendix we present the main steps for the evaluation of the integrals appearing in the expressions for the two-point functions.

2 Cylindrical electromagnetic modes

We consider \((D+1)\)-dimensional locally dS background geometry described in cylindrical spatial coordinates \((r,\phi ,{\mathbf {z}})\), \({\mathbf {z}}=( z^{3},\ldots ,z^{D})\), by the interval

$$\begin{aligned} \mathrm{d}s^{2}=(\alpha /\tau )^{2}[\mathrm{d}\tau ^{2}-\mathrm{d}r^{2}-r^{2}\mathrm{d}\phi ^{2}-(\mathrm{d}{\mathbf {z}})^{2}], \end{aligned}$$
(2.1)

with the conformal time coordinate \(\tau \), \(-\infty<\tau <0\). The corresponding synchronous time t is expressed as \(t=-\alpha \ln (\left| \tau \right| /\alpha ),\ -\infty<t<+\infty \). For the remaining coordinates we assume that \(0\leqslant r<\infty \), \(0\leqslant \phi \leqslant \phi _{0}\), \(-\infty<z^{l}<+\infty \), \(l=3,\ldots ,D\). For \( \phi _{0}=2\pi \) the geometry is reduced to the standard dS one given in inflationary coordinates. In the case \(\phi _{0}<2\pi \), though the local geometrical characteristics for \(r\ne 0\) remain the same, the global properties are different. The special case \(D=3\) corresponds to a straight cosmic string with the core along the axis \(z^{3}\) and with the planar angle deficit \(2\pi -\) \(\phi _{0}\) determined by the linear mass density of the string. In [36, 37] it has been shown that the vortex solution of the Einstein–Abelian–Higgs equations in the presence of a cosmological constant induces a deficit angle into dS spacetime. The cosmological constant \( \Lambda \) is expressed in terms of the parameter \(\alpha \) in the line element (2.1) by the relation \(\Lambda =D(D-1)/(2\alpha ^{2})\).

The presence of the angle deficit gives rise to a number of interesting topological effect in quantum field theory. Here we are interested in the influence of the cosmic string on the vacuum fluctuations of the electromagnetic field. The properties of these fluctuations are encoded in the two-point functions which describe the correlations of the fluctuations at different spacetime points. These correlators are VEVs of bilinear combinations of the vector potential operator \(A_{\mu }(x)\), where \(x=(\tau ,r,\phi ,{\mathbf {z}})\) stands for the spacetime point. By expanding this operator in terms of a complete set \(\{A_{(\beta )\mu },A_{(\beta )\mu }^{*}\}\) of solutions to the classical Maxwell equations and by using the definition of the vacuum state \(|0\rangle \), we can see that for a given bilinear combination \(f(A_{\mu }(x),A_{\nu }(x^{\prime }))\) the corresponding VEV is presented in the form of the mode sum

$$\begin{aligned} \langle 0|f(A_{\mu }(x),A_{\nu }(x^{\prime }))|0\rangle =\sum _{\beta }f(A_{(\beta )\mu }(x),A_{(\beta )\nu }^{*}(x^{\prime })). \nonumber \\ \end{aligned}$$
(2.2)

Here, the set of quantum numbers \(\beta \) specifies the electromagnetic mode functions and in the right-hand side \(\sum _{\beta }\) is understood as a summation over discrete quantum numbers and an integration over continuous ones. Hence, as the first stage, we need to find the complete set of cylindrical electromagnetic modes on dS bulk in the presence of the cosmic string.

It is convenient to fix the gauge degrees of the freedom by the Coulomb gauge with \(A_{0}=0\) and \(\partial _{l}(\sqrt{|g|}A^{l})=0\) for \(l=1,\ldots ,D\). For the metric tensor

$$\begin{aligned} g_{\mu \nu }=\big ( \alpha /\tau \big ) ^{2}\mathrm {diag} (1,-1,-r^{2},-1,\ldots ,-1), \end{aligned}$$
(2.3)

the latter equation is reduced to \(\partial _{l}(rA^{l})=0\) and coincides with the corresponding equation in the Minkowski bulk. The procedure to find the complete set of solutions to the Maxwell equations is similar to that we have already described in [38] for the bulk in the absence of the cosmic string. The only difference is in the periodicity condition along the azimuthal direction \(\phi \). The corresponding part in the mode functions is given by \(\mathrm{e}^{iqm\phi }\) with \(q=2\pi /\phi _{0}\) and \(m=0,\pm 1,\pm 2,\ldots .\) This leads to the dependence of the mode functions on the radial coordinate in terms of the Bessel function \(J_{q|m|}(\gamma r)\) with \( 0\leqslant \gamma <\infty \). The time dependence appears in the form of the linear combination of the functions \(\eta ^{D/2-1}H_{D/2-1}^{(1)}(\omega \eta )\) and \(\eta ^{D/2-1}H_{D/2-1}^{(2)}(\omega \eta )\), where \(\eta =|\tau |=\alpha \mathrm{e}^{-t/\alpha }\) and \(H_{\nu }^{(l)}(y)\), \(l=1,2\), are the Hankel functions. The relative coefficient in the linear combination depends on the choice of the vacuum state under consideration. Here we assume that the field is prepared in the state that is the analog of the Bunch–Davies vacuum state for a scalar field [39]. For this state the coefficient of the function \(H_{D/2-1}^{(2)}(\omega \eta )\) is zero.

In \((D+1)\)-dimensional spacetime, the electromagnetic field has \(D-1\) polarization states. In what follows we specify them by the quantum number \( \sigma =1,\ldots ,D-1\). For the polarization \(\sigma =1\) the cylindrical electromagnetic modes corresponding to the Bunch–Davies vacuum are presented as

$$\begin{aligned}&A_{(\beta )\mu }(x)=c_{\beta }\eta ^{D/2-1}H_{D/2-1}^{(1)}(\omega \eta )\nonumber \\&\quad \times \left( 0,\frac{iqm}{r},-r\partial _{r},0,\ldots ,0\right) J_{q|m|}(\gamma r)\mathrm{e}^{iqm\phi +i{\mathbf {k}}\cdot {\mathbf {z}}}, \nonumber \\ \end{aligned}$$
(2.4)

and for the polarizations \(\sigma =2,\ldots ,D-1\) we get

$$\begin{aligned}&A_{(\beta )\mu }(x)=c_{\beta }\omega \eta ^{D/2-1}H_{D/2-1}^{(1)}(\omega \eta )\nonumber \\&\quad \times \left( 0,\epsilon _{\sigma l}+i\frac{{\mathbf {k}}\cdot {\varvec{\epsilon }}_{\sigma }}{\omega ^{2}}\partial _{l}\right) J_{q|m|}(\gamma r)\mathrm{e}^{iqm\phi +i {\mathbf {k}}\cdot {\mathbf {z}}}, \end{aligned}$$
(2.5)

with \(l=1,\ldots ,D\). Here, \({\mathbf {k}}=(k_{3},\ldots ,k_{D})\), \(\omega = \sqrt{\gamma ^{2}+k^{2}}\) and \(k^{2}=\sum _{l=3}^{D}k_{l}^{2}\). For the scalar products one has \({\mathbf {k}}\cdot {\mathbf {z}}=\sum _{l=3}^{D}k_{l}z^{l}\) and \({\mathbf {k}}\cdot {\varvec{\epsilon }}_{\sigma }=\sum _{l=3}^{D}k_{l}\epsilon _{\sigma l}\). The spatial components in (2.4) and (2.5) are given in cylindrical coordinates \((r,\phi ,\mathbf {z })\). For the components of the polarization vector we have \(\epsilon _{\sigma 1}=\epsilon _{\sigma 2}=0\), \(\sigma =2,\ldots ,D-1\), and the relations

$$\begin{aligned}&\sum _{l,n=3}^{D}(\omega ^{2}\delta _{nl}-k_{l}k_{n}) \epsilon _{\sigma l}\epsilon _{\sigma ^{\prime }n}=\gamma ^{2}\delta _{\sigma \sigma ^{\prime }},\nonumber \\&\omega ^{2}\sum _{\sigma =2}^{D-1}\epsilon _{\sigma n}\epsilon _{\sigma l}-k_{n}k_{l}=\gamma ^{2}\delta _{nl}, \end{aligned}$$
(2.6)

for \(l,n=3,\ldots ,D\). The mode functions are specified by the set of quantum numbers \(\beta =(\gamma ,m,{\mathbf {k}},\sigma )\) and in (2.2)

$$\begin{aligned} \sum _{\beta }=\sum _{\sigma =1}^{D-1}\sum _{m=-\infty }^{\infty }\int \mathrm{d}{\mathbf {k}}\int _{0}^{\infty }\mathrm{d}\gamma . \end{aligned}$$
(2.7)

We have a single mode of the TE type (\(\sigma =1\)) and \(D-2\) modes of the TM type (\(\sigma =2,\ldots ,D-1\)).

The mode functions for vector fields are orthonormalized by the condition

$$\begin{aligned}&\int \mathrm{d}^{D}x\sqrt{|g|}g^{00}[A_{(\beta ^{\prime })\nu }^{*}(x)\nabla _{0}A_{(\beta )}^{\nu }(x)\nonumber \\&\quad -\,(\nabla _{0}A_{(\beta ^{\prime })\nu }^{*}(x))A_{(\beta )}^{\nu }(x)]=4i\pi \delta _{\beta \beta ^{\prime }}, \end{aligned}$$
(2.8)

where \(\nabla _{\mu }\) stands for the covariant derivative and \(\delta _{\beta \beta ^{\prime }}\) is understood as the Kronecker symbol for discrete components of the collective index \(\beta \) (m and \(\sigma \)) and the Dirac delta function for the continuous ones (\(\gamma \) and \({\mathbf {k}}\)). From (2.8) for the normalization coefficient \(c_{\beta }\) we get

$$\begin{aligned} |c_{\beta }|^{2}=\frac{q}{4(2\pi \alpha )^{D-3}\gamma }, \end{aligned}$$
(2.9)

for all the polarizations \(\sigma =1,\ldots ,D-1\).

The Minkowskian limit of the problem under consideration corresponds to \( \alpha \rightarrow \infty \) for a fixed value of the proper time t. In this limit one has \(\eta =\alpha \mathrm{e}^{-t/\alpha }\approx \alpha -t\) and, up to the phase (which can be absorbed into the normalization coefficient \(c_{\beta }\)), the function \(\eta ^{D/2-1}H_{D/2-1}^{(1)}(\omega \eta )\) is reduced to \(\sqrt{2/(\pi \omega )}\alpha ^{(D-3)/2}\mathrm{e}^{-i\omega t}\). As a result, from (2.4) and (2.5) one gets the corresponding mode functions for a string in background of \((D+1)\)-dimensional Minkowski spacetime. The case \( D=3\) has been considered previously in [40]. The electromagnetic field is conformally invariant in \(D=3\) and the modes (2.4) and (2.5) coincide with the Minkowskian modes having the time dependence \( \mathrm{e}^{-i\omega \eta }\).

3 Two-point functions

We consider a free field theory (the only interaction is with the background gravitational field) and all the information as regards the vacuum state is encoded in two-point functions. Given the complete set of normalized mode functions for the vector potential, we can evaluate the two-point function \( \langle 0|A_{l}(x)A_{m}(x^{\prime })|0\rangle \equiv \langle A_{l}(x)A_{m}(x^{\prime })\rangle \) for the electromagnetic field by using the mode-sum formula (2.2):

$$\begin{aligned} \langle A_{l}(x)A_{m}(x^{\prime })\rangle =\sum _{\beta }\,A_{(\beta )l}(x)A_{(\beta )m}^{*}(x^{\prime }), \end{aligned}$$
(3.1)

with \(\sum _{\beta }\) from (2.7). Substituting the functions (2.4), (2.5) and using Eq. (2.6), the two-point function is presented in the form

$$\begin{aligned}&\langle A_{l}(x)A_{p}(x^{\prime })\rangle =\frac{q(\eta \eta ^{\prime })^{D/2-1}}{\pi ^{2}(2\pi \alpha )^{D-3}} \sum _{m=-\infty }^{\infty }\mathrm{e}^{imq\Delta \phi }\int \mathrm{d}{\mathbf {k}}\,\mathrm{e}^{i{\mathbf {k}}\cdot \Delta {\mathbf {z}}}\nonumber \\&\quad \times \, \int _{0}^{\infty }\mathrm{d}\gamma \,\frac{\gamma }{\omega ^{2}} K_{D/2-1}(\mathrm{e}^{-i\pi /2}\eta \omega )K_{D/2-1}\nonumber \\&\quad \times \,(\mathrm{e}^{i\pi /2}\eta ^{\prime }\omega )f_{lp}(k,\gamma ,r,r^{\prime }), \end{aligned}$$
(3.2)

where \(\Delta \phi =\phi -\phi ^{\prime }\), \(\Delta {\mathbf {z}}={\mathbf {z}}- {\mathbf {z}}^{\prime }\) and instead of the Hankel function we have introduced the Macdonald function \(K_{\nu }(x)\). In (3.2), the functions of the radial coordinates are defined by the expressions

$$\begin{aligned} f_{11}( k,\gamma ,r,r^{\prime })= & {} k^{2}J_{q|m|}^{\prime }(\gamma r)J_{q|m|}^{\prime }(\gamma r^{\prime })\nonumber \\&+\,(k^{2}+\gamma ^{2}) \frac{q^{2}m^{2}}{\gamma ^{2}rr^{\prime }}J_{q|m|}(\gamma r)J_{q|m|}(\gamma r^{\prime }),\nonumber \\ f_{12}(k,\gamma ,r,r^{\prime })= & {} -i\frac{qm}{\gamma r}\left[ rk^{2}J_{q|m|}^{\prime }(\gamma r)J_{q|m|}(\gamma r^{\prime })\right. \nonumber \\&\left. +\,r^{\prime }\omega ^{2}J_{q|m|}^{\prime }(\gamma r^{\prime })J_{q|m|}(\gamma r)\right] ,\nonumber \\ f_{22}(k,\gamma ,r,r^{\prime })= & {} \frac{q^{2}m^{2}}{\gamma ^{2} }k^{2}J_{q|m|}(\gamma r)J_{q|m|}(\gamma r^{\prime })\nonumber \\&+\,rr^{\prime }\omega ^{2}J_{q|m|}^{\prime }(\gamma r)J_{q|m|}^{\prime }(\gamma r^{\prime }), \end{aligned}$$
(3.3)

and

$$\begin{aligned} f_{1l}(k,\gamma ,r,r^{\prime })= & {} ik_{l}\gamma J_{q|m|}^{\prime }(\gamma r)J_{q|m|}(\gamma r^{\prime }),\nonumber \\ f_{2l}(k,\gamma ,r,r^{\prime })= & {} -qmk_{l}J_{q|m|}(\gamma r)J_{q|m|}(\gamma r^{\prime }),\nonumber \\ f_{lp}(k,\gamma ,r,r^{\prime })= & {} (\omega ^{2}\delta _{lp}-k_{l}k_{p}) J_{q|m|}(\gamma r)J_{q|m|}(\gamma r^{\prime }), \nonumber \\ \end{aligned}$$
(3.4)

with \(l,p=3,\ldots ,D-1\). The remaining nonzero components are found by using the relation

$$\begin{aligned} f_{lp}(k,\gamma ,r,r^{\prime })=f_{pl}^{*}( k,\gamma ,r^{\prime },r). \end{aligned}$$
(3.5)

Having the two-point functions we can evaluate the VEVs of the squared electric and magnetic fields. For the VEV of the squared electric field one has

$$\begin{aligned} \langle E^{2}\rangle =\lim _{x^{\prime }\rightarrow x}C_{E}(x,x^{\prime }), \end{aligned}$$
(3.6)

where the corresponding two-point function is expressed as

$$\begin{aligned} C_{E}(x,x^{\prime })=-g^{00^{\prime }}(x,x^{\prime })g^{lp^{\prime }}(x,x^{\prime })\partial _{0}\partial _{0}^{\prime }\langle A_{l}(x)A_{p}(x^{\prime })\rangle , \nonumber \\ \end{aligned}$$
(3.7)

with the parallel propagator \(g^{\mu \nu ^{\prime }}(x,x^{\prime })\). For the geometry under consideration the nonzero components of the latter are given by

$$\begin{aligned} g^{00^{\prime }}(x,x^{\prime })= & {} -g^{ll^{\prime }}(x,x^{\prime })=\frac{ \eta \eta ^{\prime }}{\alpha ^{2}}, \nonumber \\ g^{11^{\prime }}(x,x^{\prime })= & {} rr^{\prime }g^{22^{\prime }}(x,x^{\prime })=-\frac{\eta \eta ^{\prime }}{\alpha ^{2}}\cos \Delta \phi , \nonumber \\ rg^{21^{\prime }}(x,x^{\prime })= & {} -r^{\prime }g^{12^{\prime }}(x,x^{\prime })=\frac{\eta \eta ^{\prime }}{\alpha ^{2}}\sin \Delta \phi , \end{aligned}$$
(3.8)

where \(l=3,\ldots ,D\).

By taking into account the representation (3.2) we find the expression

(3.9)

where

$$\begin{aligned} {\mathcal {J}}_{\nu }^{(n,p)}= & {} \int {d}{\mathbf {k}}\,\mathrm{e}^{i{\mathbf {k}}\cdot \Delta {\mathbf {z}}}\int _{0}^{\infty }{d}\gamma \,k^{2n}\gamma ^{2p-1}K_{\nu }(\mathrm{e}^{-i\pi /2}\omega \eta )\nonumber \\&\times K_{\nu }\,(\mathrm{e}^{i\pi /2}\omega \eta ^{\prime })J_{qm}(\gamma r)J_{qm}(\gamma r^{\prime }). \end{aligned}$$
(3.10)

The prime on the summation sign in (3.9) means that the term \(m=0\) should be taken with an additional coefficient 1/2. The integrals (3.10) for \(n=0,1\) and \(p=0,1,2\) are evaluated in the appendix. By using the corresponding results (A.13), (A.15) and (A.16), the correlator is presented as

(3.11)

with the notation

$$\begin{aligned} w=2rr^{\prime }u,\quad b=\frac{r^{2}+r^{\prime 2}}{2rr^{\prime }}. \end{aligned}$$
(3.12)

For the further transformation of Eq. (3.11) we use the formula [30, 31, 41]

(3.13)

where the summation in the first term on the right-hand side goes under the condition

$$\begin{aligned} -q/2+q\Delta \phi /(2\pi )\leqslant l\leqslant q/2+q\Delta \phi /(2\pi ). \end{aligned}$$
(3.14)

If \(-q/2+q\Delta \phi /(2\pi )\) or \(q/2+q\Delta \phi /(2\pi )\) are integers, then the corresponding terms in the first sum on the right-hand side of (3.13) should be taken with the coefficient 1/2. The application of (3.13) leads to the expression

$$\begin{aligned} C_{E}(x,x^{\prime })=C_{E}^{(1)}(x,x^{\prime })+\sin \Delta \phi \partial _{\Delta \phi }C_{E}^{(2)}(x,x^{\prime }). \end{aligned}$$
(3.15)

Here and below we use the notation

$$\begin{aligned}&C_{J}^{(i)}(x,x^{\prime })=\frac{8 (\eta \eta ^{\prime })^{D/2+1}}{\pi ^{D/2}\alpha ^{D+1}}\nonumber \\&\quad \times \left[ \sum _{l}g_{J}^{(i)}(x,x^{\prime },-\cos (2l\pi /q-\Delta \phi ))-\frac{q}{2\pi }\right. \nonumber \\&\quad \times \left. \sum _{j=\pm 1}\int _{0}^{\infty }\mathrm{d}y\frac{\sin (q\pi +jq\Delta \phi )g_{J}^{(i)}(x,x^{\prime },\cosh y)}{\cosh (qy)-\cos (q\pi +jq\Delta \phi )}\right] ,\nonumber \\ \end{aligned}$$
(3.16)

for \(i=1,2\) and \(J=E,M\). The function with \(J=M\) will appear in the expression for the VEV of the squared magnetic field. The functions \( g_{J}^{(i)}(x,x^{\prime },y)\) in (3.16) have the representation

$$\begin{aligned} g_{J}^{(i)}(x,x^{\prime },y)= & {} \int _{0}^{\infty }\mathrm{d}u\,u^{D/2}\mathrm{e}^{u(\eta ^{2}+\eta ^{\prime 2}-|\Delta {\mathbf {z}}|^{2}-r^{2}-r^{\prime 2}-2rr^{\prime }y)}\nonumber \\&\times \,K_{\nu _{J}}(2\eta \eta ^{\prime }u)h_{J}^{(i)}(y,u), \end{aligned}$$
(3.17)

where

$$\begin{aligned} \nu _{J}=\left\{ \begin{array}{ll} D/2-2, &{}\quad J=E ,\\ D/2-1, &{}\quad J=M. \end{array}\right. \end{aligned}$$
(3.18)

For the electric field, the functions in the integrand of (3.17) are given by the expressions

$$\begin{aligned} h_{E}^{(1)}(y,u)= & {} (D-2-y\cos \Delta \phi )[ 1-u( r^{2}+r^{\prime 2}+2rr^{\prime }y)] \nonumber \\&+\,(D-3-2y\cos \Delta \phi )( D/2-1-|\Delta {\mathbf {z}}|^{2}u), \nonumber \\ h_{E}^{(2)}(y,u)= & {} \frac{1}{2rr^{\prime }u}[u( r^{2}+r^{\prime 2}+2rr^{\prime }y) \nonumber \\&-\,2(D/2-1-|\Delta {\mathbf {z}}|^{2}u)]. \end{aligned}$$
(3.19)

The functions \(h_{M}^{(i)}(y,u)\) for the magnetic field will be defined below.

The contribution of the \(l=0\) term in (3.16) to the function (3.15) corresponds to the correlator in dS spacetime in the absence of the cosmic string (for the two-point functions of vector fields, including the massive ones; see [42,43,44,45,46,47,48]). It is simplified to

$$\begin{aligned} C_{E}^{\mathrm {(dS)}}(x,x^{\prime })= & {} \frac{2(D-1)}{(2\pi )^{D/2}\alpha ^{D+1} }\int _{0}^{\infty }\mathrm{d}u\,u^{D/2}\mathrm{e}^{uZ(x,x^{\prime })}\nonumber \\&\times \left( D-u\frac{|\Delta {{\mathbf {x}}}|^{2}}{\eta \eta ^{\prime }}\right) K_{D/2-2}(u), \end{aligned}$$
(3.20)

where \(|\Delta {\mathbf {x}}|^{2}=r^{2}+r^{\prime 2}-2rr^{\prime }\cos \Delta \phi +|\Delta {\mathbf {z}}|^{2}\) is the square of the spatial distance between the points x and \(x^{\prime }\) and we have defined the dS invariant quantity

$$\begin{aligned} Z(x,x^{\prime })=1+\frac{(\Delta \eta )^{2}-|\Delta {\mathbf {x}} |^{2}}{2\eta \eta ^{\prime }}. \end{aligned}$$
(3.21)

For the latter one has \(Z(x,x^{\prime })=\cos [\sigma (x,x^{\prime })/\alpha ]\), with \(\sigma (x,x^{\prime })\) being the proper distance along the shortest geodesic connecting the points x and \(x^{\prime }\) if they are spacelike separated. The integral in (3.20) is expressed in terms of the hypergeometric function. Separating the \(l=0\) terms in the expressions for \(C_{E}^{(1)}(x,x^{\prime })\) and \(C_{E}^{(2)}(x,x^{\prime })\), the remaining part in (3.15) corresponds to the contribution induced by the presence of the cosmic string.

For points x and \(x^{\prime }\) close to each other, the dominant contribution to the integral in (3.20) comes from large values of u and we can use the corresponding asymptotic for the function \(K_{D/2-2}(u)\). To the leading order, for the pure dS part this gives

$$\begin{aligned} C_{E}^{\mathrm {(dS)}}(x,x^{\prime })\approx & {} \frac{2(D-1)\Gamma ((D+1)/2)}{ \pi ^{(D-1)/2}\sigma ^{D+1}(x,x^{\prime })}\nonumber \\&\times \left[ D-\frac{(D+1)|\Delta {\mathbf {x}}|^{2}}{|\Delta {\mathbf {x}}|^{2}-(\Delta \eta )^{2}}\right] . \end{aligned}$$
(3.22)

In this limit the effects of the background curvature are small. Note that, for points outside the cosmic string core, \(r\ne 0\), the divergences in the coincidence limit of \(C_{E}(x,x^{\prime })\) are contained in the pure dS part \(C_{E}^{\mathrm {(dS)}}(x,x^{\prime })\) only. This is related to the fact that in our simplified model the presence of the cosmic string does not change the local geometry at those points.

4 VEV of the squared electric field

The VEV of the squared electric field is obtained from (3.15) in the coincidence limit. Separating the pure dS part \(C_{E}^{\mathrm {(dS)} }(x,x^{\prime })\), the remaining topological contribution is finite in that limit for \(r\ne 0\). Consequently, the renormalization is reduced to the one in dS spacetime. The contribution of the last term in (3.15) to the cosmic string-induced part in the VEV of the field squared vanishes. As a result, the VEV of the squared electric field is presented in the decomposed form

$$\begin{aligned} \langle E^{2}\rangle= & {} \langle E^{2}\rangle _{\mathrm {dS}}+\frac{8\alpha ^{-D-1}}{(2\pi )^{D/2}}\left[ \sum _{l=1}^{[q/2]}g_{E}(r/\eta ,s_{l})\right. \nonumber \\&\left. -\frac{q}{\pi }\sin (q\pi )\int _{0}^{\infty }\mathrm{d}y\frac{g_{E}(r/\eta ,\cosh y)}{\cosh (2qy)-\cos (q\pi )}\phantom {\sum _{l=1}^{[q/2]}}\right] , \nonumber \\ \end{aligned}$$
(4.1)

where [q / 2] is the integer part of q / 2. In (4.1), \(\langle E^{2}\rangle _{\mathrm {dS}}\) is the renormalized VEV in the absence of the cosmic string and the remaining part is induced by the cosmic string (topological part). Here and in what follows we use the notation \(s_{l}=\sin (\pi l/q)\) and

$$\begin{aligned}&g_{E}(x,y)=\int _{0}^{\infty }du\,u^{D/2}K_{D/2-2}(u)\mathrm{e}^{u-2x^{2}y^{2}u}\nonumber \\&\quad \times \,[2ux^{2}y^{2}(2y^{2}-D+1)+(D-1)(D/2-2y^{2})]. \nonumber \\ \end{aligned}$$
(4.2)

If the parameter q is equal to an even integer the term \(l=q/2\) in (4.1) should be taken with an additional coefficient 1/2. The VEV (4.1) depends on r and \(\eta \) in the form of the combination \(r/\eta \). The latter property is a consequence of the maximal symmetry of dS spacetime. Note that, for a given \(\eta \), the ratio \(\alpha r/\eta \) is the proper distance from the string. Hence, \(r/\eta \) is the proper distance measured in units of the dS curvature scale \(\alpha \). From the maximal symmetry of dS spacetime and of the Bunch–Davies vacuum state we expect that the pure dS part does not depend on the spacetime point and \(\langle E^{2}\rangle _{ \mathrm {dS}}={\mathrm {const}}\cdot \alpha ^{-D-1}\).

For odd values of D the integral in (4.2) is expressed in terms of elementary functions. In particular, for \(D=3\) and \(D=5\) one has

$$\begin{aligned} g_{E}(x,y)= & {} -\sqrt{\frac{\pi }{2}}\frac{1}{4x^{4}y^{4}},\quad D=3, \nonumber \\ g_{E}(x,y)= & {} -\sqrt{\frac{\pi }{2}}\frac{1+y^{2}}{2x^{6}y^{6}},\quad D=5. \end{aligned}$$
(4.3)

In these cases, the topological part in the squared electric field is written in terms of the function

$$\begin{aligned} c_{n}(q)= & {} \sum _{l=1}^{[q/2]}s_{l}^{-n}-\frac{q}{\pi }\sin (q\pi )\int _{0}^{\infty }\mathrm{d}y\nonumber \\&\times \frac{\cosh ^{-n}y}{\cosh (2qy)-\cos (q\pi )}. \end{aligned}$$
(4.4)

For even n, this function can be found by using the recurrence scheme described in [49]. In particular, one has \(c_{2}(q)=(q^{2}-1)/6\) and

$$\begin{aligned} c_{4}(q)= & {} \frac{q^{2}-1}{90}( q^{2}+11), \nonumber \\ c_{6}(q)= & {} \frac{q^{2}-1}{1890}(2q^{4}+23q^{2}+191). \end{aligned}$$
(4.5)

As a result, the corresponding VEVs are presented as

$$\begin{aligned} \langle E^{2}\rangle =\langle E^{2}\rangle _{\mathrm {dS}}-\frac{(q^{2}-1)(q^{2}+11) }{180\pi (\alpha r/\eta )^{4}} \end{aligned}$$
(4.6)

for \(D=3\), and

$$\begin{aligned} \langle E^{2}\rangle =\langle E^{2}\rangle _{\mathrm {dS}}-\frac{(q^{2}-1)(q^{4}+22q^{2}+211)}{1890\pi ^{2}( \alpha r/\eta )^{6}} \end{aligned}$$
(4.7)

for \(D=5\). In the case \(D=3\) the electromagnetic field is conformally invariant and the topological part in (4.6) is obtained from the corresponding result for a cosmic string in Minkowski bulk by the standard conformal transformation. The latter is reduced to the multiplication of the Minkowskian result by the factor \((\eta /\alpha )^{4}\).

As has been mentioned before, the Minkowskian limit corresponds to \( \alpha \rightarrow \infty \) for a fixed value of the time coordinate t. In this case one has \(\eta \approx \alpha -t\) and \(\eta \) is large. Hence, we need the asymptotic of the function (4.2) for small values of x. In this limit the dominant contribution to the integral comes from large values of u and using the asymptotic expression for the Macdonald function for large argument, to the leading order we find

$$\begin{aligned} g_{E}(x,y)\approx & {} -\sqrt{\pi }\frac{\Gamma ((D+1) /2)}{2^{D/2+2}x^{D+1}y^{D+1}}\nonumber \\&\times \,[2(D-3)y^{2}+D-1]. \end{aligned}$$
(4.8)

As a consequence, for a string in the Minkowski bulk one gets

$$\begin{aligned} \langle E^{2}\rangle ^{(M)}= & {} -\frac{2\Gamma ((D+1) /2)}{(4\pi )^{(D-1)/2}r^{D+1}}\left[ (D-3)c_{D-1}(q)\phantom {\frac{1}{2}}\right. \nonumber \\&\left. +\,\frac{D-1}{2}c_{D+1}(q)\right] . \end{aligned}$$
(4.9)

For \(D=3\), this result is conformally related to the topological part in (4.6). It is of interest to note that, though the electromagnetic field is not conformally invariant for \(D=5\), the latter property is valid in this case as well: \(\langle E^{2}\rangle ^{(M)}=(\langle E^{2}\rangle -\langle E^{2}\rangle _{\mathrm {dS}})( \alpha /\eta )^{D+1}\), for \(D=3,5\).

Now let us consider the asymptotic behavior of the VEV (4.1) at large and small distances from the string. At large distances, \(r/\eta \gg 1\), we need the asymptotic expressions for the function \(g_{E}(x,y)\) in the limit \( x\gg 1\). In this limit the dominant contribution to the integral in (4.2) comes from the region near the lower limit of the integration. By using the asymptotic expression for the Macdonald function for small argument, to the leading order we get

$$\begin{aligned} g_{E}(x,y)\approx & {} \frac{2^{D/2-5}}{y^{6}x^{6}}\Gamma \left( \frac{D}{2} -2\right) \left[ (D-1)\left( \frac{D}{2}-3\right) \right. \nonumber \\&\left. +\,2(4-D)y^{2}\phantom {\frac{1}{2}}\right] \end{aligned}$$
(4.10)

for \(D>4\), and \(g_{E}(x,y)\approx -3\ln (yx)/(2y^{6}x^{6})\) for \(D=4\). In the case \(D>4\) this gives

$$\begin{aligned} \langle E^{2}\rangle\approx & {} \langle E^{2}\rangle _{\mathrm {dS}}+\frac{\Gamma (D/2-2)}{4\pi ^{D/2}\alpha ^{D+1}( r/\eta )^{6}}\left[ 2(4-D)c_{4}(q)\phantom {\frac{1}{2}}\right. \nonumber \\&\left. +\,(D-1)\left( \frac{D}{2}-3\right) c_{6}(q)\right] , \end{aligned}$$
(4.11)

with the functions (4.5). Note that for \(D=5\) the asymptotic (4.11) coincides with the exact result (4.7). For \(D=4\) the large distance asymptotic is given by

$$\begin{aligned} \langle E^{2}\rangle \approx \langle E^{2}\rangle _{\mathrm {dS}}-\frac{(q^{2}-1)\ln (r/\eta )}{630\pi ^{2}\alpha ^{5}(r/\eta )^{6}} (2q^{4}+23q^{2}+191).\nonumber \\ \end{aligned}$$
(4.12)

Hence, at large distances from the string, \(r/\eta \gg 1\), the topological part in the VEV of the electric field squared decays as \((\eta /r)^{4}\) for \(D=3\), as \(\ln (r/\eta )(\eta /r)^{6}\) for \(D=4\) and as \((\eta /r)^{6}\) for \( D>4\). The pure dS part \(\langle E^{2}\rangle _{\mathrm {dS}}\) is a constant and it dominates in the total VEV at large distances. Note that at large distances from the string the influence of the gravitational field on the VEV is essential. In the Minkowskian case the decay of the VEV is as \( 1/r^{D+1}\) (see (4.9)) and depends on the number of spatial dimension. For the dS bulk the VEV behaves as \(1/r^{6}\) for all spatial dimensions \(D>4\).

At proper distances from the string smaller than the dS curvature radius one has \(r/\eta \ll 1\) and the dominant contribution to the integral in (4.2) comes from large values of u. The topological part dominates near the string and by calculations similar to those for the Minkowskian limit we get

$$\begin{aligned} \langle E^{2}\rangle \approx (\eta /\alpha )^{D+1}\langle E^{2}\rangle ^{(M)},\quad r/\eta \ll 1, \end{aligned}$$
(4.13)

with \(\langle E^{2}\rangle ^{(M)}\) given by (4.9). This result is natural because near the string the dominant contribution to the VEV comes from the fluctuations with wavelengths smaller than the curvature radius and the influence of the background gravitational field on the corresponding modes is weak.

The VEV of the electric field squared determines the Casimir–Polder interaction energy between the cosmic string and a neutral polarizable microparticle placed close to the string, \(U(r)=-\alpha _{P}\langle E^{2}\rangle \), where \(\alpha _{P}\) is the polarizability of the particle (in the absence of dispersion). The correlators of the electromagnetic field and the Casimir–Polder potential in the geometry of cosmic string on background of \(D=3\) Minkowski spacetime were investigated in [50, 51].

5 Magnetic field correlators and VEV of the energy density

As a next characteristic of the vacuum state we consider the VEV of the Lagrangian density:

$$\begin{aligned} \langle L\rangle =-\frac{1}{16\pi }g^{\mu \rho }g^{\nu \sigma }\langle F_{\mu \nu }F_{\rho \sigma }\rangle . \end{aligned}$$
(5.1)

Note that the quantity \(g^{\mu \rho }g^{\nu \sigma }\langle F_{\mu \nu }F_{\rho \sigma }\rangle \) is the Abelian analog of the gluon condensate in quantum chromodynamics. The VEV (5.1) is presented as the coincidence limit

$$\begin{aligned} \langle L\rangle =\lim _{x^{\prime }\rightarrow x}C_{L}(x,x^{\prime }), \end{aligned}$$
(5.2)

with the corresponding correlator

$$\begin{aligned} C_{L}(x,x^{\prime })=-\frac{1}{16\pi }g^{\mu \rho ^{\prime }}(x,x^{\prime })g^{\nu \sigma ^{\prime }}(x,x^{\prime }) \langle F_{\mu \nu }(x)F_{\rho \sigma }(x^{\prime })\rangle .\nonumber \\ \end{aligned}$$
(5.3)

The latter is decomposed into the electric and magnetic parts as

$$\begin{aligned} C_{L}(x,x^{\prime })=\frac{1}{8\pi }\big [ C_{E}(x,x^{\prime })-C_{M}(x,x^{\prime }\big )], \end{aligned}$$
(5.4)

where the magnetic part is given by the expression

$$\begin{aligned} C_{M}(x,x^{\prime })= & {} \frac{1}{2}g^{lm^{\prime }}(x,x^{\prime })g^{np^{\prime }}(x,x^{\prime })\langle F_{ln}(x)F_{mp}(x^{\prime })\rangle \nonumber \\= & {} [ g^{lm^{\prime }}(x,x^{\prime })g^{np^{\prime }}(x,x^{\prime })\nonumber \\&-g^{nm^{\prime }}(x,x^{\prime })g^{lp^{\prime }}(x,x^{\prime })] \partial _{l}\partial _{m^{\prime }}\langle A_{n}(x)A_{p^{\prime }}(x^{\prime })\rangle ,\nonumber \\ \end{aligned}$$
(5.5)

with the summation over the spatial indices \(l,m,n,p=1,2,\ldots ,D\) (for a scheme to measure the correlation functions for cosmological magnetic fields based on TeV blazar observations see [52]).

By using (3.2), after long calculations, the magnetic part is presented in the form

(5.6)

By taking into account the representations for the functions \({\mathcal {J}} _{\nu }^{(n,p)}\) given in the appendix, for the correlator one gets

(5.7)

The further transformation is similar to that employed for the electric field correlator. By using Eq. (3.13) we find

$$\begin{aligned} C_{M}(x,x^{\prime })=C_{M}^{(1)}(x,x^{\prime })+\sin \Delta \phi \partial _{\Delta \phi }C_{M}^{(2)}(x,x^{\prime }), \end{aligned}$$
(5.8)

where the functions \(C_{M}^{(i)}(x,x^{\prime })\) are defined in (3.16) with \(J=M\). In the corresponding definition the function \( g_{M}^{(i)}(x,x^{\prime },y)\) is given by Eq. (3.17) with the functions in the integrand

$$\begin{aligned} h_{M}^{(1)}(y,u)= & {} [1{-}(D{-}2) y\cos \Delta \phi ][1{-}u( r^{2}{+}r^{\prime 2}+2rr^{\prime }y)]\nonumber \\&+\,(D-3-2y\cos \Delta \phi )(D/2-1-|\Delta {\mathbf {z}}|^{2}u),\nonumber \\ \end{aligned}$$
(5.9)

and \(h_{M}^{(2)}(y,u)=h_{E}^{(2)}(y,u)\). The contributions of the \(l=0\) terms in (3.16)–(5.8) correspond to the correlator in dS spacetime in the absence of the cosmic string (\(q=1\)):

$$\begin{aligned}&C_{M}^{\mathrm {(dS)}}(x,x^{\prime })=\frac{2(D-1)}{(2\pi )^{D/2}\alpha ^{D+1} }\nonumber \\&\quad \times \int _{0}^{\infty }\mathrm{d}u\,u^{D/2}\mathrm{e}^{uZ(x,x^{\prime })}\left( D-u\frac{|\Delta {\mathbf {x}}|^{2}}{\eta \eta ^{\prime }}\right) K_{D/2-1}(u).\nonumber \\ \end{aligned}$$
(5.10)

For \(D=3\) the electric and magnetic correlators coincide and, hence, the correlator for the Lagrangian density vanishes. For close points x and \( x^{\prime }\), the leading term in the corresponding asymptotic expansion coincides with that for the correlator of the electric field, \(C_{M}^{ \mathrm {(dS)}}(x,x^{\prime })\approx C_{E}^{\mathrm {(dS)}}(x,x^{\prime })\), and is given by (3.22).

In (5.8), separating the \(l=0\) terms in the expressions (3.16) for the functions \(C_{M}^{(i)}(x,x^{\prime })\), the remaining part is the contribution induced by the cosmic string. For \(r\ne 0\), the latter is finite in the coincidence limit. The renormalization is required for the pure dS part only. Hence, for the VEV of the squared magnetic field,

$$\begin{aligned} \langle B^{2}\rangle =\lim _{x^{\prime }\rightarrow x}C_{M}(x,x^{\prime }), \end{aligned}$$
(5.11)

one finds the decomposition

$$\begin{aligned} \langle B^{2}\rangle= & {} \langle B^{2}\rangle _{\mathrm {dS}}+\frac{8\alpha ^{-D-1}}{(2\pi )^{D/2}}\left[ \sum _{l=1}^{[q/2]}g_{M}(r/\eta ,s_{l})\right. \nonumber \\&\left. -\,\frac{q }{\pi }\sin (q\pi )\int _{0}^{\infty }\mathrm{d}y\frac{g_{M}(r/\eta ,\cosh y)}{\cosh (2qy)-\cos (q\pi )}\right] ,\nonumber \\ \end{aligned}$$
(5.12)

with the function

$$\begin{aligned} g_{M}(x,y)= & {} \int _{0}^{\infty }\mathrm{d}u\,u^{D/2}K_{D/2-1}(u)\mathrm{e}^{u-2x^{2}y^{2}u}\{ (D{-}1)D/2 \nonumber \\&-\,4(D{-}2)y^{2}{+}2x^{2}y^{2}u[2(D{-}2)y^{2}{-}D{+}1]\}.\nonumber \\ \end{aligned}$$
(5.13)

Similar to (4.1), if q / 2 is an integer, the term \(l=q/2\) in (5.12) should be taken with an additional coefficient 1/2. Note that for \(D>3\) the magnetic part of the field tensor is not a spatial vector. In (5.12), \(\langle B^{2}\rangle _{\mathrm {dS}}\) is the corresponding renormalized quantity in the absence of the cosmic string and, because of the maximal symmetry of dS spacetime, does not depend on the spacetime point. From the dimensional arguments we expect that \(\langle B^{2}\rangle _{\mathrm {dS}}= {\mathrm {const}}\cdot \alpha ^{-D-1}\). For \(D=3\), the VEV of the squared magnetic field has been investigated in [53] by using the adiabatic renormalization procedure. In this special case \(\langle B^{2}\rangle _{ \mathrm {dS}}=19/(40\pi \alpha ^{4})\) (note the different units used here and in [53]).

For odd D, the function \(g_{M}(x,y)\) is expressed in terms of the elementary functions. In particular, for \(D=3\) it coincides with \(g_{E}(x,y)\), given by (4.3), and for \(D=5\) one has

$$\begin{aligned} g_{M}(x,y)=\sqrt{\frac{\pi }{2}}\frac{\big ( 3+x^{2}\big ) y^{2}-1}{ 2x^{6}y^{6}},\quad D=5. \end{aligned}$$
(5.14)

In the latter case, the VEV of the squared magnetic field is presented as

$$\begin{aligned} \langle B^{2}\rangle =\langle B^{2}\rangle _{\mathrm {dS}}+\frac{( 3+r^{2}/\eta ^{2}) c_{4}(q)-c_{6}(q)}{2\pi ^{2}(\alpha r/\eta ) ^{6}}, \end{aligned}$$
(5.15)

where the functions \(c_{4}(q)\) and \(c_{6}(q)\) are defined in (4.5).

Let us consider the asymptotic behavior of the VEV (5.12) at large and small distances from the string. If the proper distance from the string is much smaller than the curvature radius of the dS spacetime one has \(r/\eta \ll 1\). For small x the dominant contribution to (5.13) comes from large values of u. By using the corresponding asymptotic for the Macdonald function, to the leading order we get

$$\begin{aligned} \langle B^{2}\rangle \approx (\eta /\alpha ) ^{D+1}\langle B^{2}\rangle ^{(M)}, \end{aligned}$$
(5.16)

where

$$\begin{aligned}&\langle B^{2}\rangle ^{(M)}=\frac{2\Gamma ((D+1)/2)}{(4\pi )^{(D-1)/2}r^{D+1}}\nonumber \\&\quad \times \left[ (D-3)(D-2)c_{D-1}(q)-\frac{D-1 }{2}c_{D+1}(q)\right] \end{aligned}$$
(5.17)

is the corresponding VEV for the cosmic string in Minkowski bulk. In particular, for \(D=3\) one has \(\langle B^{2}\rangle ^{(M)}=\langle E^{2}\rangle ^{(M)}\) with \(\langle E^{2}\rangle ^{(M)}\) given by the last term in the right-hand side of (4.6).

At large distances from the string, \(r/\eta \gg 1\), we need the asymptotic of the function \(g_{M}(x,y)\) for large x. In this limit, the dominant contribution to the integral in (5.13) comes from the region near the lower limit of the integration and for the leading term one finds

$$\begin{aligned} g_{M}(x,y)\approx \frac{2^{D/2-5}}{y^{4}x^{4}}(D-1)( D-4) \Gamma (D/2-1). \end{aligned}$$
(5.18)

For \(D=4\) the leading term vanishes and we need to consider the next to the leading contribution:

$$\begin{aligned} g_{M}(x,y)\approx \frac{y^{2}-3/4}{y^{6}x^{6}}. \end{aligned}$$
(5.19)

By taking into account (4.5) and (5.18), at distances \(r/\eta \gg 1\) one gets

$$\begin{aligned} \langle B^{2}\rangle\approx & {} \langle B^{2}\rangle _{\mathrm {dS}}+\frac{ (D-1)( D-4)\Gamma (D/2-1)}{360\pi ^{D/2}\alpha ^{D+1}(r/\eta )^{4}}\nonumber \\&\times \,(q^{2}-1)(q^{2}+11) \end{aligned}$$
(5.20)

for \(D\ne 4\), and

$$\begin{aligned} \langle B^{2}\rangle \approx \langle B^{2}\rangle _{\mathrm {dS}}+\frac{4c_{4}(q)-3c_{6}(q)}{2\pi ^{2}\alpha ^{5}(r/\eta )^{6}} \end{aligned}$$
(5.21)

for \(D=4\). In the special case \(D=3\), the asymptotic (5.20) coincides with the exact result.

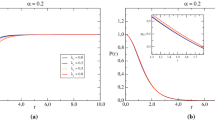
In Fig. 1 we have plotted the topological contributions in the VEVs of the squared electric and magnetic fields, \(\langle F^{2}\rangle _{t}=\langle F^{2}\rangle -\langle F^{2}\rangle _{\mathrm {dS}}\), \(F=E,B\), for \(q=2.5\) and for spatial dimensions \(D=3,4,5\) (the numbers near the curves). The full/dashed curves correspond to the electric/magnetic fields. In the case \(D=3\) one has \(\langle E^{2}\rangle _{t}=\langle B^{2}\rangle _{t}\). Note that for \(D=4,5\) the VEVs of the squared electric and magnetic fields have opposite signs. The Casimir–Polder forces acting on a polarizable particle are attractive.

Fig. 1
figure 1

Topological contributions in the VEVs of the squared electric and magnetic fields for \(q=2.5\) and for spatial dimensions \(D=3,4,5\) (the numbers near the curves). The full/dashed curves correspond to the electric/magnetic fields

Full size image

Among the most interesting features of the inflation is the transition from quantum-to-classical behavior of quantum fluctuations during the quasi-exponential expansion of the universe. An important example of this type of effects is the classicalization of the vacuum fluctuations of the inflaton field which underlies the most popular models of generation of large-scale structure in the universe. A similar effect of classicalization should take place for the electromagnetic fluctuations. In [53], the quantum-to-classical transition of super-Hubble magnetic modes during inflation has been considered as a possible mechanism for the generation of galactic and galaxy cluster magnetic fields (see also [54, 55] for the further discussion). As has been discussed above, the presence of a cosmic string induces shifts in the VEVs of the squared electric and magnetic fields. As a consequence of the quantum-to-classical transition of the corresponding fluctuations during the dS expansion, after inflation these shifts will be imprinted as classical stochastic fluctuations of the electric and magnetic fields surrounding the cosmic string. In the post inflationary radiation dominated era the conductivity is high and the currents in the cosmic plasma eliminate the electric fields whereas the magnetic counterparts are frozen. As a consequence, the cosmic strings will be surrounded by large-scale magnetic fields. These fields would be among the distinctive features of the cosmic strings produced during the inflation and also of the corresponding inflationary models. Note that various types of mechanisms for the generation of primordial magnetic fields from cosmic strings in the post-inflationary era have been discussed in the literature (see, for instance, [56,57,58,59,60,61,62,63]). For cosmic strings carrying a nonzero magnetic flux in the core, azimuthal currents for charged fields are generated around the string (see [30, 31] and the references therein). These currents provide another mechanism for the generation of magnetic fields by the cosmic strings.

Having the VEVs for the squared electric and magnetic fields, we can find the VEV of the energy density \(\varepsilon \) as

$$\begin{aligned} \langle \varepsilon \rangle =\frac{\langle E^{2}\rangle +\langle B^{2}\rangle }{8\pi }. \end{aligned}$$
(5.22)

It is decomposed into the pure dS part, \(\langle \varepsilon \rangle _{ \mathrm {dS}}\), and the topological contribution:

$$\begin{aligned} \langle \varepsilon \rangle= & {} \langle \varepsilon \rangle _{\mathrm {dS}}+ \frac{2\alpha ^{-D-1}}{(2\pi )^{D/2+1}}\left[ \sum _{l=1}^{[q/2]}g_{0}(r/\eta ,s_{l})\right. \nonumber \\&\left. -\frac{q}{\pi }\sin (q\pi )\int _{0}^{\infty }\mathrm{d}y\frac{g_{0}(r/\eta ,\cosh y)}{\cosh (2qy)-\cos (q\pi )}\phantom {\sum _{l=1}^{[q/2]}}\right] , \end{aligned}$$
(5.23)

with \(g_{0}(x,y)=g_{E}(x,y)+g_{M}(x,y)\). If q is equal to an even integer, the term \(l=q/2\) in (5.23) is taken with an additional coefficient 1/2. From the maximal symmetry of the dS spacetime it follows that \(\langle \varepsilon \rangle _{\mathrm {dS}}={\mathrm {const}}/\alpha ^{D+1}\). In the special case \(D=3\) the latter is completely determined by the conformal anomaly (see, for instance, [64]): \(\langle \varepsilon \rangle _{ \mathrm {dS}}=31/(480\pi ^{2}\alpha ^{4})\). Combining this with the result for \(\langle B^{2}\rangle _{\mathrm {dS}}\) we can find the VEV of the squared electric field: \(\langle E^{2}\rangle _{\mathrm {dS}}=1/(24\pi \alpha ^{4})\). In this case, the contributions of the electric and magnetic parts to the topological term in the VEV of the energy density are the same and the VEV is conformally related to the corresponding result on the Minkowski bulk found in [65, 66].

Near the string, \(r/\eta \ll 1\), the VEV of the energy density is dominated by the topological part and to the leading order one has

$$\begin{aligned} \langle \varepsilon \rangle\approx & {} \frac{\Gamma (( D+1)/2)}{(4\pi )^{(D+1)/2}(\alpha r/\eta )^{D+1}}[(D-3)^{2}c_{D-1}(q)\nonumber \\&-\,(D-1)c_{D+1}(q)]. \end{aligned}$$
(5.24)

The corresponding VEV in the Minkowski bulk is obtained from the right-hand side multiplying by the factor \((\alpha /\eta )^{D+1}\). Depending on the parameters D and q, the energy density (5.24) can be either negative or positive. For \(D=3\) it is always negative. At large distances from the cosmic string and for \(D>4\) the topological contribution in the energy density is dominated by the magnetic part and decays as \((\eta /r)^{4} \). For \(D=4\) and at large distances the electric part dominates and the energy density decays like \((\eta /r)^{6}\ln (r/\eta )\). In Fig. 2 we display the dependence of the topological contribution in the vacuum energy density as a function of the proper distance from the string (measured in units of dS curvature scale). The graphs are plotted for spatial dimensions \(D=3,4,5\). As is seen, in general, the energy density is not a monotonic function of the distance from the string. Moreover, in the case \(D=5\) the energy density changes the sign: it is negative near the string (the electric part dominates) and positive at large distances from the string (the magnetic contribution dominates).

Fig. 2
figure 2

Topological contributions in the VEV of the energy density in spatial dimensions \(D=3,4,5\) (the numbers near the curves) for \(q=2.5\)

Full size image

6 Conclusion

In the present paper we have investigated the influence of the cosmic string on the vacuum fluctuations of the electromagnetic field in background of \( (D+1)\)-dimensional dS spacetime, assuming that the field is prepared in the state which is the analog of the Bunch–Davies vacuum state for a scalar field. In the problem under consideration the only interaction of the quantum electromagnetic field is with the background gravitational field and the information on the vacuum fluctuations is encoded in the two-point functions. As such we have considered the Wightman function. For the evaluation of the latter we have used the direct summation over the complete set of electromagnetic cylindrical modes. The corresponding mode functions for separate polarizations are given by (2.4) and (2.5).

Among the most important characteristics of the electromagnetic vacuum are the VEVs of the squared electric and magnetic fields. The corresponding two-point functions are given by (3.15) and (5.7), respectively, with the function \(C_{J}^{(i)}(x,x^{\prime })\) defined in (3.16). One of the advantages for these representations is that the contribution corresponding to dS spacetime in the absence of the cosmic string is explicitly extracted. In the model of the cosmic string under consideration the local geometrical characteristics outside the string core are not changed by the presence of the string. Consequently, the divergences and the renormalization procedure for the VEVs are the same as those in pure dS spacetime. The topological parts do not require a renormalization. The renormalized VEVs for the squared electric and magnetic fields are presented in the decomposed form, Eqs. (4.1) and (5.12), respectively, where the first terms in the right-hand sides correspond to the renormalized VEVs in dS spacetime in the absence of the cosmic string. As a consequence of the maximal symmetry of dS spacetime and of the Bunch–Davies vacuum state these contributions do not depend on the spacetime coordinates.

The topological parts in the VEVs depend on the time and the radial coordinate through the ratio \(r/\eta \), which represents the proper distance from the string measured in units of the dS curvature radius. Near the string, the dominant contribution to the VEVs comes from the fluctuations with short wavelengths and the VEVs coincide with those for the string in Minkowski bulk with the distance from the string replaced by the proper distance \(\alpha r/\eta \). The influence of the gravitational field on the topological contributions in the VEVs is crucial at proper distances larger than the curvature radius of the background geometry. This contribution in the electric field squared decays as \((\eta /r)^{4}\) for \(D=3\), as \(\ln (r/\eta )(\eta /r)^{6}\) for \(D=4\) and as \((\eta /r)^{6}\) for \(D>4\). For the squared magnetic field the topological contribution decays as \((\eta /r)^{4}\) for \(D\geqslant 3\). The exception is the case \(D=4\) where the corresponding coefficient vanishes and the next term in the expansion should be kept. In this case the topological term falls off as \((\eta /r)^{6}\). In the Minkowskian bulk the decay of the VEVs is as \(1/r^{D+1}\) for both the electric and the magnetic fields.

The modifications of the electromagnetic field vacuum fluctuations during the dS expansion phase, we have discussed here, will be imprinted in large-scale stochastic perturbations of the electromagnetic fields surrounding the cosmic string in the post-inflationary radiation dominated era. The magnetic fields will be frozen in the cosmic plasma whereas the electric fields will be eliminated by the induced currents.

We have also investigated the VEV of the electromagnetic energy density, induced by a cosmic string. Near the string the topological contribution dominates in the total VEV and the energy density behaves as \((\eta /r)^{D+1} \). At distances from the string larger than the curvature radius of the dS spacetime and for spatial dimensions \(D>4\), the topological part in the energy density is dominated by the magnetic contribution and decays as \((\eta /r)^{4}\). For \(D=4\) the electric field contribution dominates and at large distances the string-induced energy density behaves as \((\eta /r)^{6}\ln (r/\eta )\). For \(D=3\) the topological contribution in the energy density is negative and decays as \((\eta /r)^{4}\) for all distances. For other spatial dimensions the energy density, in general, is not a monotonic function of the distance from the string. For example, in the case \(D=5\) the energy density is negative near the string and positive at large distances. It has a maximum for some intermediate value of the distance from the string.