1 Introduction

In the past years, several new charmed baryon states have been observed, and the spectroscopy of the charmed baryon states have re-attracted much attention [1], the QCD sum rules plays an important roles in assigning those new baryon states. The masses of the heavy baryon states with \(J^P={\frac{1}{2}}^\pm \), \({\frac{3}{2}}^\pm \), \({\frac{5}{2}}^\pm \) have been studied with the full QCD sum rules [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] or the QCD sum rules combined with the heavy quark effective theory [19,20,21,22,23,24,25,26,27,28].

Recently, the LHCb collaboration studied the \(\Xi _c^+ K^-\) mass spectrum with a sample of pp collision data corresponding to an integrated luminosity of \(3.3~\mathrm {fb}^{-1}\) collected by the LHCb experiment, and one observed five new narrow excited \(\Omega _c^0\) states, \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\), \(\Omega _c(3119)\) [29]. The measured masses and widths are

$$\begin{aligned}&\Omega _c(3000) : M = 3000.4 \pm 0.2 \pm 0.1 \text{ MeV } ,\nonumber \\&\quad \, \Gamma = 4.5\pm 0.6\pm 0.3 \text{ MeV } , \nonumber \\&\Omega _c(3050) : M = 3050.2 \pm 0.1 \pm 0.1 \text{ MeV } ,\nonumber \\&\quad \, \Gamma = 0.8\pm 0.2\pm 0.1 \text{ MeV } , \nonumber \\&\Omega _c(3066) : M = 3065.6 \pm 0.1 \pm 0.3 \text{ MeV } ,\nonumber \\&\quad \, \Gamma = 3.5\pm 0.4\pm 0.2 \text{ MeV } , \nonumber \\&\Omega _c(3090) : M = 3090.2 \pm 0.3 \pm 0.5 \text{ MeV } ,\nonumber \\&\quad \, \Gamma = 8.7\pm 1.0\pm 0.8 \text{ MeV } , \nonumber \\&\Omega _c(3119) : M = 3119.1 \pm 0.3 \pm 0.9 \text{ MeV } ,\nonumber \\&\quad \, \Gamma = 1.1\pm 0.8\pm 0.4 \text{ MeV } . \end{aligned}$$
(1)

There have been several assignments for those new charmed states. In Ref. [30], \(\Omega _c(3066)\) and \(\Omega _c(3119)\) are assigned to the 2S \(\Omega _c^0\) states with \(J^P={\frac{1}{2}}^+\) and \({\frac{3}{2}}^+\), respectively. In Ref. [31], possible assignments of those \(\Omega _c^0\) states to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\) are discussed. In Refs. [32,33,34], the \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) and \(\Omega _c(3119)\) are assigned to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\), respectively. In Refs. [35, 36], those \(\Omega _c^0\) states are assigned to the pentaquark states or molecular pentaquark states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\) or \({\frac{5}{2}}^-\). In Ref. [37], \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\) and \(\Omega _c(3090)\) are assigned to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{1}{2}}^-\), respectively. In Ref. [38], \(\Omega _c(3090)\) and \(\Omega _c(3119)\) are assigned to the 2S \(\Omega _c^0\) states with \(J^P={\frac{1}{2}}^+\) and \({\frac{3}{2}}^+\), respectively, while \(\Omega _c(3000)\), \(\Omega _c(3066)\) and \(\Omega _c(3050)\) are assigned to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\), respectively.

In this article, we tentatively assign \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) and \(\Omega _c(3119)\) to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\), respectively, and study their masses and pole residues with the QCD sum rules in detail.

The ground state quarks have the spin-parity \({1\over 2}^+\), two quarks can form a scalar diquark or an axialvector diquark with the spin-parity \(0^+\) or \(1^+\), the diquark then combines with a third quark to form a positive parity baryon with spin \({1\over 2}\) or \({3\over 2}\). We can construct the baryon currents \(\eta \) and \(\eta _\mu \) with positive parity without introducing additional P-wave. As multiplying \(i \gamma _{5}\) to the baryon currents changes their parity, the currents \(i \gamma _{5}\eta \) and \(i \gamma _{5}\eta _\mu \) couple potentially to the negative parity heavy baryon states. In Refs. [17, 18], we construct the currents without introducing relative P-wave to study the negative parity heavy, doubly heavy and triply heavy baryon states, and obtain satisfactory results. The predictions \(M=2.98\pm 0.16 \,\mathrm {GeV}\) for the \(\Omega _c^0\) states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\) are consistent with the masses of \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) from the LHCb collaboration [17].

In Ref. [39], we construct the interpolating currents by introducing the relative P-wave explicitly, study the negative parity charmed baryon states \(\Lambda _c(2625)\) and \(\Xi _c(2815)\) with the full QCD sum rules, and reproduce the experimental values of the masses. In this article, we extend our previous work to study \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) and \(\Omega _c(3119)\) with QCD sum rules by introducing the relative P-wave explicitly.

The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the \(\Omega _c^0\) states in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusions.

2 QCD sum rules for the \(\Omega _c^0\) states

In the following, we write down the two-point correlation functions \(\Pi (p)\), \(\Pi _{\mu \nu }(p)\), \(\Pi _{\mu \nu \alpha \beta }(p)\) in the QCD sum rules,

$$\begin{aligned}&\Pi (p)=i\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \langle 0|T\left\{ J(x)\bar{J}(0)\right\} |0\rangle , \nonumber \\&\Pi _{\mu \nu }(p)=i\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \langle 0|T\left\{ J_{\mu }(x)\bar{J}_{\nu }(0)\right\} |0\rangle , \nonumber \\&\Pi _{\mu \nu \alpha \beta }(p)=i\int \mathrm{d}^4x \mathrm{e}^{ip \cdot x} \langle 0|T\left\{ J_{\mu \nu }(x)\bar{J}_{\alpha \beta }(0)\right\} |0\rangle , \end{aligned}$$
(2)

where \(J(x)=J^1(x),\,J^2(x)\), \(J_\mu (x)=J^1_\mu (x),\,J^2_\mu (x)\),

$$\begin{aligned} J^1(x)= & {} i\varepsilon ^{ijk} \left[ \partial ^\mu s^T_i(x) C\gamma ^\nu s_j(x)+ s^T_i(x) C\gamma ^\nu \partial ^{\mu }s_j(x)\right] \nonumber \\&g_{\mu \nu }\,c_k(x) , \nonumber \\ J^2(x)= & {} i\varepsilon ^{ijk} \left[ \partial ^\mu s^T_i(x) C\gamma ^\nu s_j(x)+ s^T_i(x) C\gamma ^\nu \partial ^{\mu }s_j(x)\right] \nonumber \\&\sigma _{\mu \nu }\,c_k(x) ,\nonumber \\ J^1_{\mu }(x)= & {} i\varepsilon ^{ijk} \left[ \partial ^\alpha s^T_i(x) C\gamma ^\beta s_j(x)+s^T_i(x) C\gamma ^\beta \partial ^{\alpha }s_j(x)\right] \nonumber \\&\left( \widetilde{g}_{\mu \alpha }\gamma _\beta -\widetilde{g}_{\mu \beta }\gamma _\alpha \right) \gamma _5 c_k(x) ,\nonumber \\ J^2_{\mu }(x)= & {} i\varepsilon ^{ijk} \left[ \partial ^\alpha s^T_i(x) C\gamma ^\beta s_j(x)+ s^T_i(x) C\gamma ^\beta \partial ^{\alpha }s_j(x)\right] \nonumber \\&\left( g_{\mu \alpha }\gamma _\beta +g_{\mu \beta }\gamma _\alpha -\frac{1}{2}g_{\alpha \beta }\gamma _\mu \right) \gamma _5 c_k(x) ,\nonumber \\ J_{\mu \nu }(x)= & {} i\varepsilon ^{ijk} \left[ \partial _\mu s^T_i(x) C\gamma _\nu s_j(x)+\partial _\nu s^T_i(x) C\gamma _\mu s_j(x)\right. \nonumber \\&\left. +\,\, s^T_i(x) C\gamma _\nu \partial _{\mu }s_j(x)\right. \nonumber \\&\left. +\,\, s^T_i(x) C\gamma _\mu \partial _{\nu }s_j(x)\right] c_k(x), \end{aligned}$$
(3)

\(\widetilde{g}_{\mu \nu }=g_{\mu \nu }-\frac{1}{4}\gamma _\mu \gamma _\nu \), i, j, k are color indices, C is the charge conjugation matrix. We construct the currents with the light diquarks \(S^{i}_{\mu \nu }=\varepsilon ^{ijk} [ \partial _\mu s^T_i C\gamma _\nu s_j+ s^T_i C\gamma _\nu \partial _{\mu }s_j]\). The \(S^{i}_{\mu \nu }\) have two Lorentz indices \(\mu \) and \(\nu \), but they are neither symmetric nor anti-symmetric when interchanging the indices \(\mu \) and \(\nu \). The scalar components \(S^{i}_{\mu \nu }g^{\mu \nu }\) and \(S^{i}_{\mu \nu }\sigma ^{\mu \nu }\) couple potentially to the spin-0 diquarks. The Dirac matrices \(\widetilde{g}^{\alpha \mu }\gamma ^\nu -\widetilde{g}^{\alpha \nu }\gamma ^\mu \) and \(g^{\alpha \mu }\gamma ^\nu +g^{\alpha \nu }\gamma ^\mu -\frac{1}{2}g^{\mu \nu }\gamma ^\alpha \) are anti-symmetric and symmetric, respectively, when interchanging the indices \(\mu \) and \(\nu \), the vector components \(S^{i}_{\mu \nu }(\widetilde{g}^{\alpha \mu }\gamma ^\nu -\widetilde{g}^{\alpha \nu }\gamma ^\mu ) \) and \(S^{i}_{\mu \nu }(g^{\alpha \mu }\gamma ^\nu +g^{\alpha \nu }\gamma ^\mu -\frac{1}{2}g^{\mu \nu }\gamma ^\alpha )\) couple potentially to the spin-1 diquarks. The symmetric components \(S^{i}_{\mu \nu }+S^{i}_{\nu \mu }\) couple potentially to the spin-0 and 2 diquarks. So we choose the currents J(x), \(J_\mu (x)\) and \(J_{\mu \nu }(x)\) to study the spin-\(\frac{1}{2}\), \(\frac{3}{2}\) and \(\frac{5}{2}\) baryon states, respectively.

The currents J(0), \(J_\mu (0)\) and \(J_{\mu \nu }(0)\) couple potentially to the \({\frac{1}{2}}^-\), \({\frac{1}{2}}^+\), \({\frac{3}{2}}^-\) and \({\frac{1}{2}}^-\), \({\frac{3}{2}}^+\), \({\frac{5}{2}}^-\) charmed baryon states \(B_{\frac{1}{2}}^{-}\), \(B_{\frac{1}{2}}^{+}\), \(B_{\frac{3}{2}}^{-}\) and \(B_{\frac{1}{2}}^{-}\), \(B_{\frac{3}{2}}^{+}\), \(B_{\frac{5}{2}}^{-}\), respectively,

$$\begin{aligned}&\langle 0| J (0)|B_{\frac{1}{2}}^{-}(p)\rangle =\lambda ^{-}_{\frac{1}{2}} U^{-}(p,s) , \end{aligned}$$
(4)
$$\begin{aligned}&\langle 0| J_{\mu } (0)|B_{\frac{1}{2}}^{+}(p)\rangle =f^{+}_{\frac{1}{2}}p_\mu U^{+}(p,s) , \nonumber \\&\langle 0| J_{\mu } (0)|B_{\frac{3}{2}}^{-}(p)\rangle =\lambda ^{-}_{\frac{3}{2}} U^{-}_\mu (p,s) , \end{aligned}$$
(5)
$$\begin{aligned}&\langle 0| J_{\mu \nu } (0)|B_{\frac{1}{2}}^{-}(p)\rangle =g^{-}_{\frac{1}{2}}p_\mu p_\nu U^{-}(p,s) , \nonumber \\&\langle 0| J_{\mu \nu } (0)|B_{\frac{3}{2}}^{+}(p)\rangle =f^{+}_{\frac{3}{2}} \left[ p_\mu U^{+}_{\nu }(p,s)+p_\nu U^{+}_{\mu }(p,s)\right] , \nonumber \\&\langle 0| J_{\mu \nu } (0)|B_{\frac{5}{2}}^{-}(p)\rangle =\lambda ^{-}_{\frac{5}{2}} U^{-}_{\mu \nu }(p,s) . \end{aligned}$$
(6)

The currents J(0), \(J_\mu (0)\) and \(J_{\mu \nu }(0)\) also couple potentially to the \({\frac{1}{2}}^+\), \({\frac{1}{2}}^-\), \({\frac{3}{2}}^+\) and \({\frac{1}{2}}^+\), \({\frac{3}{2}}^-\), \({\frac{5}{2}}^+\) charmed baryon states \(B_{\frac{1}{2}}^{+}\), \(B_{\frac{1}{2}}^{-}\), \(B_{\frac{3}{2}}^{+}\) and \(B_{\frac{1}{2}}^{+}\), \(B_{\frac{3}{2}}^{-}\), \(B_{\frac{5}{2}}^{+}\), respectively [42,43,44],

$$\begin{aligned}&\langle 0| J (0)|B_{\frac{1}{2}}^{+}(p)\rangle =\lambda ^{+}_{\frac{1}{2}} i\gamma _5 U^{+}(p,s) , \end{aligned}$$
(7)
$$\begin{aligned}&\langle 0| J_{\mu } (0)|B_{\frac{1}{2}}^{-}(p)\rangle =f^{-}_{\frac{1}{2}}p_\mu i\gamma _5 U^{-}(p,s) , \nonumber \\&\langle 0| J_{\mu } (0)|B_{\frac{3}{2}}^{+}(p)\rangle =\lambda ^{+}_{\frac{3}{2}}i\gamma _5 U^{+}_{\mu }(p,s) , \end{aligned}$$
(8)
$$\begin{aligned}&\langle 0| J_{\mu \nu } (0)|B_{\frac{1}{2}}^{+}(p)\rangle =g^{+}_{\frac{1}{2}}p_\mu p_\nu i\gamma _5 U^{+}(p,s) , \nonumber \\&\langle 0| J_{\mu \nu } (0)|B_{\frac{3}{2}}^{-}(p)\rangle =f^{-}_{\frac{3}{2}} i\gamma _5\left[ p_\mu U^{-}_{\nu }(p,s)+p_\nu U^{-}_{\mu }(p,s)\right] , \nonumber \\&\langle 0| J_{\mu \nu } (0)|B_{\frac{5}{2}}^{+}(p)\rangle =\lambda ^{+}_{\frac{5}{2}}i\gamma _5 U^{+}_{\mu \nu }(p,s) . \end{aligned}$$
(9)

The spinors \(U^\pm (p,s)\) satisfy the Dirac equations \((\not \!\!p-M_{\pm })U^{\pm }(p)=0\), while the spinors \(U^{\pm }_\mu (p,s)\) and \(U^{\pm }_{\mu \nu }(p,s)\) satisfy the Rarita–Schwinger equations \((\not \!\!p-M_{\pm })U^{\pm }_\mu (p)=0\) and \((\not \!\!p-M_{\pm })U^{\pm }_{\mu \nu }(p)=0\), and the relations \(\gamma ^\mu U^{\pm }_\mu (p,s)=0\), \(p^\mu U^{\pm }_\mu (p,s)=0\), \(\gamma ^\mu U^{\pm }_{\mu \nu }(p,s)=0\), \(p^\mu U^{\pm }_{\mu \nu }(p,s)=0\), \( U^{\pm }_{\mu \nu }(p,s)= U^{\pm }_{\nu \mu }(p,s)\). The \(\lambda ^{\pm }_{\frac{1}{2}/\frac{3}{2}/\frac{5}{2}}\), \(f^{\pm }_{\frac{1}{2}/\frac{3}{2}}\) and \(g^{\pm }_{\frac{1}{2}}\) are the pole residues or current-baryon coupling constants.

At the phenomenological side, we insert a complete set of intermediate charmed baryon states with the same quantum numbers as the current operators J(x), \(i\gamma _5 J(x)\), \(J_\mu (x)\), \(i\gamma _5 J_\mu (x)\), \(J_{\mu \nu }(x)\) and \(i\gamma _5 J_{\mu \nu }(x)\) into the correlation functions \(\Pi (p)\), \(\Pi _{\mu \nu }(p)\) and \(\Pi _{\mu \nu \alpha \beta }(p)\) to obtain the hadronic representation [40, 41]. After isolating the pole terms of the lowest states of the charmed baryon states, we obtain the following results:

$$\begin{aligned} \Pi (p) = {\lambda ^{-}_{\frac{1}{2}}}^2 {\!\not \!{p}+ M_{-} \over M_{-}^{2}-p^{2} } + {\lambda ^{+}_{\frac{1}{2}}}^2 {\!\not \!{p}- M_{+} \over M_{+}^{2}-p^{2} } +\ldots , \end{aligned}$$
(10)
$$\begin{aligned} \Pi _{\mu \nu }(p)= & {} {\lambda ^{-}_{\frac{3}{2}}}^2 {\!\not \!{p}+ M_{-} \over M_{-}^{2}-p^{2} }\nonumber \\&\times \left( - g_{\mu \nu }+\frac{\gamma _\mu \gamma _\nu }{3}+\frac{2p_\mu p_\nu }{3p^2}-\frac{p_\mu \gamma _\nu -p_\nu \gamma _\mu }{3\sqrt{p^2}} \right) \nonumber \\&+\, {\lambda ^{+}_{\frac{3}{2}}}^2 {\!\not \!{p}- M_{+} \over M_{+}^{2}-p^{2} }\nonumber \\&\times \left( - g_{\mu \nu }+\frac{\gamma _\mu \gamma _\nu }{3}+\frac{2p_\mu p_\nu }{3p^2}-\frac{p_\mu \gamma _\nu -p_\nu \gamma _\mu }{3\sqrt{p^2}} \right) \nonumber \\&+\, {f^{+}_{\frac{1}{2}}}^2 {\!\not \!{p}+ M_{+} \over M_{+}^{2}-p^{2} } p_\mu p_\nu \nonumber \\&+\, {f^{-}_{\frac{1}{2}}}^2 {\!\not \!{p}- M_{-} \over M_{-}^{2}-p^{2} } p_\mu p_\nu +\ldots , \end{aligned}$$
(11)
$$\begin{aligned} \Pi _{\mu \nu \alpha \beta }(p)= & {} {\lambda ^{-}_{\frac{5}{2}}}^2 {\!\not \!{p}+ M_{-} \over M_{-}^{2}-p^{2} } \Biggl [\frac{ \widetilde{g}_{\mu \alpha }\widetilde{g}_{\nu \beta }+\widetilde{g}_{\mu \beta }\widetilde{g}_{\nu \alpha }}{2}-\frac{\widetilde{g}_{\mu \nu }\widetilde{g}_{\alpha \beta }}{5}\nonumber \\&-\frac{1}{10}\left( \gamma _{\mu }\gamma _{\alpha }+\frac{\gamma _{\mu }p_{\alpha }-\gamma _{\alpha }p_{\mu }}{\sqrt{p^2}}-\frac{p_{\mu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\nu \beta }\nonumber \\&-\frac{1}{10}\left( \gamma _{\nu }\gamma _{\alpha }+\frac{\gamma _{\nu }p_{\alpha }-\gamma _{\alpha }p_{\nu }}{\sqrt{p^2}}-\frac{p_{\nu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\mu \beta } +\cdots \Biggr ]\nonumber \\&+\, {\lambda ^{+}_{\frac{5}{2}}}^2 {\!\not \!{p}- M_{+} \over M_{+}^{2}-p^{2} } \Biggl [\frac{ \widetilde{g}_{\mu \alpha }\widetilde{g}_{\nu \beta }+\widetilde{g}_{\mu \beta }\widetilde{g}_{\nu \alpha }}{2} -\frac{\widetilde{g}_{\mu \nu }\widetilde{g}_{\alpha \beta }}{5}\nonumber \\&-\frac{1}{10}\left( \gamma _{\mu }\gamma _{\alpha }+\frac{\gamma _{\mu }p_{\alpha }-\gamma _{\alpha }p_{\mu }}{\sqrt{p^2}}-\frac{p_{\mu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\nu \beta }\nonumber \\&-\frac{1}{10}\left( \gamma _{\nu }\gamma _{\alpha }+\frac{\gamma _{\nu }p_{\alpha }-\gamma _{\alpha }p_{\nu }}{\sqrt{p^2}}-\frac{p_{\nu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\mu \beta } +\cdots \Biggr ] \nonumber \\&+\,{f^{+}_{\frac{3}{2}}}^2 {\!\not \!{p}+ M_{+} \over M_{+}^{2}-p^{2} } \Biggl [ p_\mu p_\alpha \Biggl (- g_{\nu \beta }+\frac{\gamma _\nu \gamma _\beta }{3}\nonumber \\&+\,\frac{2p_\nu p_\beta }{3p^2}-\frac{p_\nu \gamma _\beta -p_\beta \gamma _\nu }{3\sqrt{p^2}} \Biggr )+\cdots \Biggr ]\nonumber \\&+ \,{f^{-}_{\frac{3}{2}}}^2 {\!\not \!{p}- M_{-} \over M_{-}^{2}-p^{2} } \Biggl [ p_\mu p_\alpha \Biggl (- g_{\nu \beta }+\frac{\gamma _\nu \gamma _\beta }{3}\nonumber \\&+\,\frac{2p_\nu p_\beta }{3p^2}-\frac{p_\nu \gamma _\beta -p_\beta \gamma _\nu }{3\sqrt{p^2}} \Biggr )+\cdots \Biggr ] \nonumber \\&+\, {g^{-}_{\frac{1}{2}}}^2 {\!\not \!{p}+ M_{-} \over M_{-}^{2}-p^{2} } p_\mu p_\nu p_\alpha p_\beta \nonumber \\&+\, {g^{+}_{\frac{1}{2}}}^2 {\!\not \!{p}- M_{+} \over M_{+}^{2}-p^{2} } p_\mu p_\nu p_\alpha p_\beta +\ldots , \end{aligned}$$
(12)

where \(\widetilde{g}_{\mu \nu }=g_{\mu \nu }-\frac{p_{\mu }p_{\nu }}{p^2}\). In calculations, we have used the following summations [45]:

$$\begin{aligned} \sum _s U \overline{U}= & {} \left( \!\not \!{p}+M_{\pm }\right) , \end{aligned}$$
(13)
$$\begin{aligned}&\sum _s U_\mu \overline{U}_\nu =\left( \!\not \!{p}+M_{\pm }\right) \nonumber \\&\quad \times \left( -g_{\mu \nu }+\frac{\gamma _\mu \gamma _\nu }{3}+\frac{2p_\mu p_\nu }{3p^2}-\frac{p_\mu \gamma _\nu -p_\nu \gamma _\mu }{3\sqrt{p^2}} \right) , \end{aligned}$$
(14)
$$\begin{aligned} \sum _s U_{\mu \nu }\overline{U}_{\alpha \beta }= & {} \left( \!\not \!{p}+M_{\pm }\right) \left\{ \frac{\widetilde{g}_{\mu \alpha }\widetilde{g}_{\nu \beta }+\widetilde{g}_{\mu \beta }\widetilde{g}_{\nu \alpha }}{2} -\frac{\widetilde{g}_{\mu \nu }\widetilde{g}_{\alpha \beta }}{5} \right. \nonumber \\&\left. -\frac{1}{10}\left( \gamma _{\mu }\gamma _{\alpha }+\frac{\gamma _{\mu }p_{\alpha }-\gamma _{\alpha }p_{\mu }}{\sqrt{p^2}}-\frac{p_{\mu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\nu \beta }\right. \nonumber \\&-\frac{1}{10}\left( \gamma _{\nu }\gamma _{\alpha }+\frac{\gamma _{\nu }p_{\alpha }-\gamma _{\alpha }p_{\nu }}{\sqrt{p^2}}-\frac{p_{\nu }p_{\alpha }}{p^2}\right) \widetilde{g}_{\mu \beta }\nonumber \\&-\frac{1}{10}\left( \gamma _{\mu }\gamma _{\beta }+\frac{\gamma _{\mu }p_{\beta }-\gamma _{\beta }p_{\mu }}{\sqrt{p^2}}-\frac{p_{\mu }p_{\beta }}{p^2}\right) \widetilde{g}_{\nu \alpha }\nonumber \\&\left. -\frac{1}{10}\left( \gamma _{\nu }\gamma _{\beta }+\frac{\gamma _{\nu }p_{\beta }-\gamma _{\beta }p_{\nu }}{\sqrt{p^2}}-\frac{p_{\nu }p_{\beta }}{p^2}\right) \widetilde{g}_{\mu \alpha } \right\} ,\nonumber \\ \end{aligned}$$
(15)

and \(p^2=M^2_{\pm }\) on the mass shell.

We can rewrite the correlation functions \(\Pi (p)\), \(\Pi _{\mu \nu }(p)\) and \(\Pi _{\mu \nu \alpha \beta }(p)\) into the following form according to Lorentz covariance:

$$\begin{aligned}&\Pi (p)=\Pi _{\frac{1}{2}}(p^2) , \end{aligned}$$
(16)
$$\begin{aligned}&\Pi _{\mu \nu }(p)=\Pi _{\frac{3}{2}}(p^2)\,\left( - g_{\mu \nu }\right) +\ldots , \end{aligned}$$
(17)
$$\begin{aligned}&\Pi _{\mu \nu \alpha \beta }(p)=\Pi _{\frac{5}{2}}(p^2)\,\frac{ g_{\mu \alpha }g_{\nu \beta }+g_{\mu \beta }g_{\nu \alpha }}{2}+\ldots . \end{aligned}$$
(18)

In this article, we choose the tensor structures \(g_{\mu \nu }\) and \(g_{\mu \alpha }g_{\nu \beta }+g_{\mu \beta }g_{\nu \alpha }\) for analysis, and separate the contributions of the \({\frac{3}{2}}^{\pm }\) and \({\frac{5}{2}}^{\pm }\) charmed baryon states unambiguously. For a detailed discussion of this subject, one can consult Ref. [44].

We obtain the hadronic spectral densities at phenomenological side through the dispersion relation,

$$\begin{aligned} \frac{\mathrm{Im}\Pi _{j}(s)}{\pi }= & {} \!\not \!{p} [{\lambda ^{-}_{j}}^2 \delta (s-M_{-}^2)+{\lambda ^{+}_{j}}^2 \delta (s-M_{+}^2)] \nonumber \\&+[M_{-}{\lambda ^{-}_{j}}^2 \delta (s-M_{-}^2)-M_{+}{\lambda ^{+}_{j}}^2 \delta (s-M_{+}^2)], \nonumber \\= & {} \not \!\!{p}\, \rho ^1_{j,H}(s)+\rho ^0_{j,H}(s) , \end{aligned}$$
(19)

where \(j=\frac{1}{2}\), \(\frac{3}{2}\), \(\frac{5}{2}\), the subscript H denotes the hadron side, then we introduce the weight function \(\exp (-\frac{s}{T^2})\) to obtain the QCD sum rules at the phenomenological side,

$$\begin{aligned}&\int _{m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j,H}(s)+\rho ^0_{j,H}(s)\right] \exp \left( -\frac{s}{T^2}\right) \nonumber \\&\quad =2M_{-}{\lambda ^{-}_{j}}^2\exp \left( -\frac{M_{-}^2}{T^2}\right) , \end{aligned}$$
(20)

where the \(s_0\) are the continuum thresholds and the \(T^2\) are the Borel parameters [44].

At the QCD side, we calculate the light quark parts of the correlation functions \(\Pi (p)\), \(\Pi _{\mu \nu }(p)\), \(\Pi _{\mu \nu \alpha \beta }(p)\) with the full light quark propagators in the coordinate space and take the momentum space expression for the full c-quark propagator. It is straightforward but tedious to compute the integrals both in the coordinate and momentum spaces to obtain the correlation functions \(\Pi _{j}(p^2)\), therefore we obtain the QCD spectral densities through the dispersion relation,

$$\begin{aligned} \frac{\mathrm{Im}\Pi _{j}(s)}{\pi }= & {} \!\not \!{p}\, \rho ^1_{j,QCD}(s)+\rho ^0_{j,QCD}(s) , \end{aligned}$$
(21)

where \(j=\frac{1}{2}\), \(\frac{3}{2}\), \(\frac{5}{2}\), the explicit expressions of the QCD spectral densities \(\rho ^1_{j,QCD}(s)\) and \(\rho ^0_{j,QCD}(s)\) are neglected for simplicity. In this article, we carry out the operator product expansion up to the vacuum condensates of dimension 10 and take into account the vacuum condensates \(\langle \bar{s}s\rangle \), \(\langle \frac{\alpha _sGG}{\pi }\rangle \), \(\langle \bar{s}g_s\sigma Gs\rangle \), \(\langle \bar{s}s\rangle \langle \bar{s}g_s\sigma Gs\rangle \), \(\langle \bar{s}g_s\sigma Gs\rangle ^2\).

Once the analytical QCD spectral densities \(\rho ^1_{j,QCD}(s)\) and \(\rho ^0_{j,QCD}(s)\) are obtained, we can take the quark–hadron duality below the continuum thresholds \(s_0\) and introduce the weight function \(\exp (-\frac{s}{T^2})\) to obtain the QCD sum rules:

$$\begin{aligned}&2M_{-}{\lambda ^{-}_{j}}^2\exp \left( -\frac{M_{-}^2}{T^2}\right) \nonumber \\&\quad = \int _{m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j,QCD}(s)+\rho ^0_{j,QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) .\nonumber \\ \end{aligned}$$
(22)

We derive Eq. (22) with respect to \(\frac{1}{T^2}\), then eliminate the pole residues \(\lambda ^{-}_j\) and obtain the QCD sum rules for the masses of the charmed baryon states,

$$\begin{aligned} M^2_{-}= & {} \frac{-\frac{\mathrm{d}}{\mathrm{d}(1/T^2)}\int _{m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j,QCD}(s)+\rho ^0_{j,QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) }{\int _{m_c^2}^{s_0}\mathrm{d}s \left[ \sqrt{s}\rho ^1_{j,QCD}(s)+\rho ^0_{j,QCD}(s)\right] \exp \left( -\frac{s}{T^2}\right) }.\nonumber \\ \end{aligned}$$
(23)

3 Numerical results and discussions

The vacuum condensates are taken to be the standard values \(\langle \bar{q}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3\), \(\langle \bar{s}s \rangle =(0.8\pm 0.1)\langle \bar{q}q \rangle \), \(\langle \bar{s}g_s\sigma G s \rangle =m_0^2\langle \bar{s}s \rangle \), \(m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2\), \(\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33\,\mathrm {GeV})^4 \) at the energy scale \(\mu =1\, \mathrm {GeV}\) [40, 41, 46]. The quark condensate and mixed quark condensate evolve with the renormalization group equation, \(\langle \bar{s}s \rangle (\mu )=\langle \bar{s}s \rangle (Q)[\frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}]^{\frac{4}{9}}\), \(\langle \bar{s}g_s \sigma Gs \rangle (\mu )=\langle \bar{s}g_s \sigma Gs \rangle (Q)[\frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}]^{\frac{2}{27}}\).

Table 1 The Borel parameters \(T^2\), continuum threshold parameters \(s_0\), pole contributions (pole) and perturbative contributions (perturbative)
Full size table
Fig. 1
figure 1

The masses of the charmed baryon states with variations of the Borel parameters \(T^2\), where (1) and (2) correspond to the currents \(J^1_\mu \) and \(J^2_\mu \), respectively

Full size image
Fig. 2
figure 2

The pole residues of the charmed baryon states with variations of the Borel parameters \(T^2\), where (1) and (2) correspond to the currents \(J^1_\mu \) and \(J^2_\mu \), respectively

Full size image

In the article, we take the \(\overline{MS}\) masses \(m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}\) and \(m_s(\mu =2\,\mathrm {GeV})=(0.095\pm 0.005)\,\mathrm {GeV}\) from the particle data group [1], and take into account the energy-scale dependence of the \(\overline{MS}\) masses from the renormalization group equation,

$$\begin{aligned} m_c(\mu )= & {} m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}} \, ,\nonumber \\ m_s(\mu )= & {} m_s(\mathrm{2\,\,\, GeV} )\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(\mathrm{2\, GeV})}\right] ^{\frac{4}{9}},\nonumber \\ \alpha _s(\mu )= & {} \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$
(24)

where \(t=\log \frac{\mu ^2}{\Lambda ^2}\), \(b_0=\frac{33-2n_f}{12\pi }\), \(b_1=\frac{153-19n_f}{24\pi ^2}\), \(b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}\), \(\Lambda =213\), 296 and \(339\,\mathrm {MeV}\) for the flavors \(n_f=5\), 4 and 3, respectively [1].

In Refs. [47,48,49,50,51], we study the acceptable energy scales of the QCD spectral densities for the hidden-charm (bottom) tetraquark states and molecular states in the QCD sum rules for the first time, and we suggest the empirical formula \(\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}\) to determine the optimal energy scales, where X, Y, Z denote the four-quark states, and \({\mathbb {M}}_Q\) is the effective heavy quark mass. The empirical energy-scale formula also works well in studying the hidden-charm pentaquark states [44]. In Ref. [39], we use the diquark–quark model to construct the interpolating currents, and take the analogous formula \( \mu =\sqrt{M_{\Lambda _c/\Xi _c}^2-{\mathbb {M}}_c^2}\) to determine the energy scales of the QCD spectral densities of the QCD sum rules for the charmed baryon states \(\Lambda _c(2625)\) and \(\Xi _c(2815)\), and obtain satisfactory results. In this article, we use the formula \(\mu =\sqrt{M_{\Omega _c}^2-{\mathbb {M}}_c^2}\) to determine the energy scales of the QCD spectral densities. If we take the updated value \({\mathbb {M}}_c=1.82\,\mathrm {GeV}\) [52], then \(\mu \approx 2.5\,\mathrm {GeV}\). In calculations, we set the energy scales of the QCD spectral densities to be \(\mu =2.5\,\mathrm {GeV}\).

Now we search for the Borel parameters \(T^2\) and continuum threshold parameters \(s_0\) to satisfy the following three criteria:

  1. 1.

    pole dominance at the phenomenological side;

  2. 2.

    convergence of the operator product expansion;

  3. 3.

    appearance of the Borel platforms.

In calculations, we observe that no stable QCD sum rules can be obtained for the current \(J^2(x)\). The resulting Borel parameters \(T^2\), continuum threshold parameters \(s_0\), pole contributions and perturbative contributions (per) are shown explicitly in Table 1, where the perturbative contributions are defined by

$$\begin{aligned} \mathrm{per}= & {} \frac{\int _{m_c^2}^{s_0}\mathrm{d}s\,\rho _{ \mathrm{per}}(s)\exp \left( -\frac{s}{T^2}\right) }{\int _{m_c^2}^{s_0}\mathrm{d}s\,\rho _{ \mathrm{tot}}(s)\exp \left( -\frac{s}{T^2}\right) } , \end{aligned}$$
(25)

\(\rho _{ \mathrm{per}}(s)\) and \(\rho _{ \mathrm{tot}}(s)\) denote the perturbative and total QCD spectral densities, respectively. From the table, we can see that the criteria \(\mathbf 1\) and \(\mathbf 2\) can be satisfied.

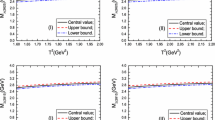
We take into account all uncertainties of the relevant parameters, and we obtain the values of the masses and pole residues of the \(\Omega _c^0\) baryon states, which are shown in Figs.1, 2 and Table 2. In Figs.1, 2, we plot the masses and pole residues with variations of the Borel parameters at much larger intervals than the Borel windows shown in Table 1. In the Borel windows, the uncertainties originating with the Borel parameters in the Borel windows are very small, \(\delta M_{\Omega _c}/M_{\Omega _c}=(1.2-1.6)\%\), the criterion \(\mathbf 3\) is also satisfied. The three criteria are all satisfied, we expect to make reliable predictions. In Figs. 1 and 2 and Table 2, we also present the possible assignments of the \(\Omega _c^0\) states according to the masses.

In Ref. [17], we choose the currents without introducing the relative P-wave to study the negative parity heavy and doubly heavy baryon states, and we obtain the predictions \(M=2.98\pm 0.16 \,\mathrm {GeV}\) for the \(\Omega _c^0\) states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), where the diquark constituent \(\varepsilon ^{ijk}s^T_jC\gamma _\mu s_k\) is taken to construct the currents. Multiplying \(i \gamma _{5}\) to the baryon currents changes their parity, we can choose currents without introducing relative P-wave to study the P-wave baryon states. The current \(\varepsilon ^{ijk}s^{T}_{j}C\gamma _\mu s_k \gamma ^{\mu } c_{i}\) couples potentially to the \(\Omega _c^0\) state with \(J^P={\frac{1}{2}}^-\) [17], the mass of the \(\Omega _c(3000)\) is in excellent agreement with the prediction \(M=2.98\pm 0.16 \,\mathrm {GeV}\) [17] or the prediction\(M=2.990\pm 0.129\,\mathrm {GeV}\) based on a more general interpolating current with additional parameter [53], the \(\Omega _c(3000)\) can be assigned to the P-wave charmed baryon state with \(J^{P}={\frac{1}{2}}^-\), where two s quarks are in relative S-wave. In Table 3, we present some predictions for the masses of the P-wave \(\Omega _c^0\) baryon states from the full QCD sum rules [17, 53, 54] and potential quark models [55,56,57,58]. We cannot identify a baryon state unambiguously with the mass alone; it is necessary to study the decay widths of those P-wave baryon states with the QCD sum rules. In Ref. [53], Agaev, Azizi and Sundu study the masses and widths of the 1P \({\frac{1}{2}}^-\), \({\frac{3}{2}}^-\) and 2S \({\frac{1}{2}}^+\), \({\frac{3}{2}}^+\) \(\Omega _c^0\) baryon states with the full QCD sum rules, and they assign \(\Omega _c(3000)\), \(\Omega _c(3050)\) and \(\Omega _c(3119)\) to the \(\Omega _c^0\) baryon states with the quantum numbers \((\mathrm{1P},\,\frac{1}{2}^{-})\), \((\mathrm{1P},\,\frac{3}{2}^{-})\) and \((\mathrm{2S},\,\frac{3}{2}^{+})\), respectively, and assign the \(\Omega _c(3066)\) or \(\Omega _c(3090)\) to the \(\Omega _c^0\) baryon state with the quantum numbers \((\mathrm{2S},\,\frac{1}{2}^{+})\).

Table 2 The masses M, pole residues \(\lambda \) and possible assignments of the charmed baryon states, where \(j_l\) denotes the total angular momentum of the light degree of freedom
Full size table
Table 3 The masses of the P-wave \(\Omega _c\) baryon states, where the unit is GeV, \(j_l\) denotes the total angular momentum of the light degree of freedom. We neglect the mixing effects of the \({\frac{1}{2}}^{-}_{0}-{\frac{1}{2}}^{-}_{1}\) and \({\frac{3}{2}}^{-}_{1}-{\frac{3}{2}}^{-}_{2}\) in the potential quark models for simplicity
Full size table

4 Conclusion

In this article, we assign \(\Omega _c(3000)\), \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) and \(\Omega _c(3119)\) to the P-wave charmed baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\), respectively, and we study their masses and pole residues with the QCD sum rules in detail by introducing an explicit relative P-wave between the two constituents of the light diquarks. The predictions support assigning \(\Omega _c(3050)\), \(\Omega _c(3066)\), \(\Omega _c(3090)\) and \(\Omega _c(3119)\) to the P-wave baryon states with \(J^P={\frac{1}{2}}^-\), \({\frac{3}{2}}^-\), \({\frac{3}{2}}^-\) and \({\frac{5}{2}}^-\), respectively, where the two constituents of the light diquark are in relative P-wave; while the \(\Omega _c(3000)\) can be assigned to the P-wave charmed baryon state with \(J^{P}={\frac{1}{2}}^-\), where the two constituents of the light diquark are in relative S-wave.